3.3.1利用去括号解一元一次方程 课件(共16张PPT) 人教版数学七年级上册
文档属性
| 名称 | 3.3.1利用去括号解一元一次方程 课件(共16张PPT) 人教版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 11:39:11 | ||
图片预览





文档简介
(共16张PPT)
3.3 解一元一次方程(二)
——去括号与去分母
第1课时 利用去括号解一元一次方程
甲码头
乙码头
已知水流速度3 km/h,
顺流行驶用了2 h,
用了2.5 h
一艘船从甲码头到乙码头顺流行驶,
从乙码头返回甲码头逆流行驶,
,求船在静水中的速度?
流水行船
去括号解方程的应用
二
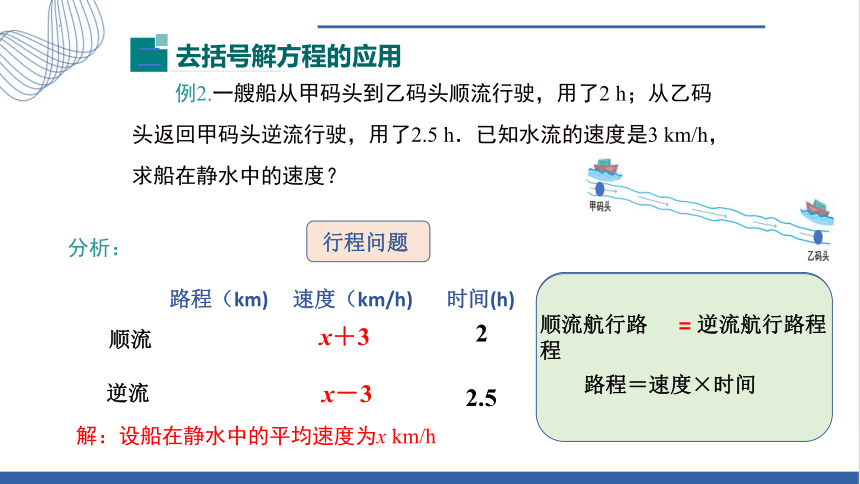
例2.一艘船从甲码头到乙码头顺流行驶,用了2 h;从乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度?
分析:
行程问题
路程(km)
时间(h)
速度(km/h)
逆流
顺流
水流速度
静水速度
顺水速度
逆水速度
2.5
+
2
=
=
-
静水速度
水流速度
解:设船在静水中的平均速度为x km/h
3
3
x
x
x+3
x-3
x+3
x-3
顺流航行路程
逆流航行路程
=
路程=速度×时间
去括号解方程的应用
二
顺流速度___顺流时间___逆流速度___逆流时间
×
=
×
例2.一艘船从甲码头到乙码头顺流行驶,用了2 h;从乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度?
分析:
解:设船在静水中的平均速度为x km/h
(x+3)
(x-3)
2
2.5
×
=
×
等量关系:顺流航行路程=逆流航行路程,
去括号解方程的应用
二
例2.一艘船从甲码头到乙码头顺流行驶,用了2 h;从乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度?
解:设船在静水中的平均速度为x km/h
(x+3)
(x-3)
2
2.5
×
=
×
顺流速度___顺流时间___逆流速度___逆流时间
×
=
×
分析:等量关系:顺流航行路程=逆流航行路程,
这个方程如何解呢?
很明显,我们无法通过移项、合并同类项、系数化为1解这个方程,因为这个方程
有括号
有括号,我们就要
去括号
2 (x+3) = 2.5 (x-3)
解方程:
用乘法分配律和去括号法则填空
a + (– b + c ) =
2x+3(3x + 4) =
–(7y–5)=
m-2(–m+n)=
法则 :
括号前是“+"号,把括号和它前面的“+"号去掉,括号里各项都不变号
a+(b+c)=a+b+c
法则 :
括号前是“—"号,把括号和它前面的“—"号去掉,括号里各项都变号
a-(b+c)=a-b-c
a-b+c
11x+12
-7y+5
3m-2n
2 (x+3) = 2.5 (x-3)
2x
2×3
+6
2.5x
2.5×(﹣3)
﹣7.5
=
解:去括号,得:
移项,得:
合并同类项,得:
系数化为1,得:
2x-2.5x=-7.5-6
-0.5x=-13.5
x=27
答:船在静水中的速度为27km/h.
例2.一艘船从甲码头到乙码头顺流行驶,用了2 h;从乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度?
解:船在静水中的平均速度为x km/h
去括号的依据是什么?
去括号法则,乘法分配律
解一元一次方程时,按照去括号法则,把方程中的括号去掉,这个过程叫做去括号。
解一元一次方程的步骤:
去括号
移项
合并同类项
系数化为1
1.解下列方程:
去括号,得:
2x-x-10=5x+2x-2
移项,得:
2x-x-5x-2x=-2+10
合并同类项,得:
-6x=8
系数化为1,得:
x=-
去括号,得:
3x-7x+7=3-2x-6
移项,得:
3x-7x+2x=3-6-7
合并同类项,得:
-2x=-10
系数化为1,得:
x=5
练一练
2.一架飞机在两城之间航行,风速为24 km/h,顺风
飞行要2小时50分,逆风飞行要3小时,求两城距离.
解:设飞机在无风时的速度为x km/h,则在顺风中的速度为(x+24) km/h ,在逆风中的速度为(x-24) km/h.
根据题意,得
解得
两城市的距离为
答:两城市之间的距离为2 448 km.
练一练
3.某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 度,全年用电15 万度.这个工厂去年上半年每月平均用电是多少?
月平均用电量(度) 总用电量(度)
上半年
下半年
全年
月平均用电量×n(月数)=n个月用电量
(x-2000)
x
6x
6(x-2000)
15 万度
分析:设上半年每月平均用电 度,则下半年每月平均用电为( x-2 0度.
上半年共用电 度;下半年共用电 度.
全年共用了15万度电,所以,可列方程:
(x-2000)
6x
6(x-2000)
6x+6(x -2 000)=150000
x
练一练
6x+6 ( x -2 000 )=150000
去括号:
6x+6x-12000=150000
移项:
6x+6x=150000+12000
合并同类项:
12x=162000
系数化为1:
x=13500
答:这个工厂去年上半年每月平均用电是13500度。
3.某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 度,全年用电15 万度.这个工厂去年上半年每月平均用电是多少?
解:设上半年每月平均用电 x 度
课堂小结
3.至此,解一元一次方程的步骤:
1.怎样从实际问题中抽象出方程?
相等关系
数量关系
设元
列方程
2.今天学习了用什么新方法解一元一次方程 依据是什么
去括号 → 移项 → 合并同类项 → 系数化为1
去括号;乘法分配律和去括号法则
(1) 6x =-2(3x-5) +10; (2) -2(x+5)=3(x-5)-6
1.解下列方程
解:
(1) 6x=-2(3x-5)+10
6x=-6x+10+10
6x +6x=10+10
12x=20
(2) -2(x+5)=3(x-5)-6
-2x-10=3x-15-6
-2x-3x=-15-6+10
-5x=-11
小试牛刀
当堂练习
2.某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000度,全年用电15万度,这个工厂去年上半年每月平均用电多少度?
答案:这个工厂去年上半年每月平均用电13500度.
3.两辆汽车从相距 84 km 的两地同时出发相向而行,甲车的速度比乙车的速度快20 km/h,半小时后两车相遇,两车的速度各是多少
答案:甲车速度为94km/h,乙车速度为94km/h
3.3 解一元一次方程(二)
——去括号与去分母
第1课时 利用去括号解一元一次方程
甲码头
乙码头
已知水流速度3 km/h,
顺流行驶用了2 h,
用了2.5 h
一艘船从甲码头到乙码头顺流行驶,
从乙码头返回甲码头逆流行驶,
,求船在静水中的速度?
流水行船
去括号解方程的应用
二
例2.一艘船从甲码头到乙码头顺流行驶,用了2 h;从乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度?
分析:
行程问题
路程(km)
时间(h)
速度(km/h)
逆流
顺流
水流速度
静水速度
顺水速度
逆水速度
2.5
+
2
=
=
-
静水速度
水流速度
解:设船在静水中的平均速度为x km/h
3
3
x
x
x+3
x-3
x+3
x-3
顺流航行路程
逆流航行路程
=
路程=速度×时间
去括号解方程的应用
二
顺流速度___顺流时间___逆流速度___逆流时间
×
=
×
例2.一艘船从甲码头到乙码头顺流行驶,用了2 h;从乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度?
分析:
解:设船在静水中的平均速度为x km/h
(x+3)
(x-3)
2
2.5
×
=
×
等量关系:顺流航行路程=逆流航行路程,
去括号解方程的应用
二
例2.一艘船从甲码头到乙码头顺流行驶,用了2 h;从乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度?
解:设船在静水中的平均速度为x km/h
(x+3)
(x-3)
2
2.5
×
=
×
顺流速度___顺流时间___逆流速度___逆流时间
×
=
×
分析:等量关系:顺流航行路程=逆流航行路程,
这个方程如何解呢?
很明显,我们无法通过移项、合并同类项、系数化为1解这个方程,因为这个方程
有括号
有括号,我们就要
去括号
2 (x+3) = 2.5 (x-3)
解方程:
用乘法分配律和去括号法则填空
a + (– b + c ) =
2x+3(3x + 4) =
–(7y–5)=
m-2(–m+n)=
法则 :
括号前是“+"号,把括号和它前面的“+"号去掉,括号里各项都不变号
a+(b+c)=a+b+c
法则 :
括号前是“—"号,把括号和它前面的“—"号去掉,括号里各项都变号
a-(b+c)=a-b-c
a-b+c
11x+12
-7y+5
3m-2n
2 (x+3) = 2.5 (x-3)
2x
2×3
+6
2.5x
2.5×(﹣3)
﹣7.5
=
解:去括号,得:
移项,得:
合并同类项,得:
系数化为1,得:
2x-2.5x=-7.5-6
-0.5x=-13.5
x=27
答:船在静水中的速度为27km/h.
例2.一艘船从甲码头到乙码头顺流行驶,用了2 h;从乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度?
解:船在静水中的平均速度为x km/h
去括号的依据是什么?
去括号法则,乘法分配律
解一元一次方程时,按照去括号法则,把方程中的括号去掉,这个过程叫做去括号。
解一元一次方程的步骤:
去括号
移项
合并同类项
系数化为1
1.解下列方程:
去括号,得:
2x-x-10=5x+2x-2
移项,得:
2x-x-5x-2x=-2+10
合并同类项,得:
-6x=8
系数化为1,得:
x=-
去括号,得:
3x-7x+7=3-2x-6
移项,得:
3x-7x+2x=3-6-7
合并同类项,得:
-2x=-10
系数化为1,得:
x=5
练一练
2.一架飞机在两城之间航行,风速为24 km/h,顺风
飞行要2小时50分,逆风飞行要3小时,求两城距离.
解:设飞机在无风时的速度为x km/h,则在顺风中的速度为(x+24) km/h ,在逆风中的速度为(x-24) km/h.
根据题意,得
解得
两城市的距离为
答:两城市之间的距离为2 448 km.
练一练
3.某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 度,全年用电15 万度.这个工厂去年上半年每月平均用电是多少?
月平均用电量(度) 总用电量(度)
上半年
下半年
全年
月平均用电量×n(月数)=n个月用电量
(x-2000)
x
6x
6(x-2000)
15 万度
分析:设上半年每月平均用电 度,则下半年每月平均用电为( x-2 0度.
上半年共用电 度;下半年共用电 度.
全年共用了15万度电,所以,可列方程:
(x-2000)
6x
6(x-2000)
6x+6(x -2 000)=150000
x
练一练
6x+6 ( x -2 000 )=150000
去括号:
6x+6x-12000=150000
移项:
6x+6x=150000+12000
合并同类项:
12x=162000
系数化为1:
x=13500
答:这个工厂去年上半年每月平均用电是13500度。
3.某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 度,全年用电15 万度.这个工厂去年上半年每月平均用电是多少?
解:设上半年每月平均用电 x 度
课堂小结
3.至此,解一元一次方程的步骤:
1.怎样从实际问题中抽象出方程?
相等关系
数量关系
设元
列方程
2.今天学习了用什么新方法解一元一次方程 依据是什么
去括号 → 移项 → 合并同类项 → 系数化为1
去括号;乘法分配律和去括号法则
(1) 6x =-2(3x-5) +10; (2) -2(x+5)=3(x-5)-6
1.解下列方程
解:
(1) 6x=-2(3x-5)+10
6x=-6x+10+10
6x +6x=10+10
12x=20
(2) -2(x+5)=3(x-5)-6
-2x-10=3x-15-6
-2x-3x=-15-6+10
-5x=-11
小试牛刀
当堂练习
2.某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000度,全年用电15万度,这个工厂去年上半年每月平均用电多少度?
答案:这个工厂去年上半年每月平均用电13500度.
3.两辆汽车从相距 84 km 的两地同时出发相向而行,甲车的速度比乙车的速度快20 km/h,半小时后两车相遇,两车的速度各是多少
答案:甲车速度为94km/h,乙车速度为94km/h
