人教版八年级数学上册11.1.2 三角形的高、中线与角平分线 (14张ppt)
文档属性
| 名称 | 人教版八年级数学上册11.1.2 三角形的高、中线与角平分线 (14张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 12:52:31 | ||
图片预览



文档简介
(共14张PPT)
第十一章 三角形
11.1 与三角形有关的线段
11.1.2 三角形的高、中线
与角平分线
1.掌握三角形的高,中线及角平分线的概念及其画法.
2.能应用三角形的高、中线和角平分线的概念进行简单的计算.
任务一:掌握三角形的高,中线及角平分线的概念及其画法.
定义:从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
A
B
C
D
注意:标明垂直的记号和垂足的字母.
活动1:什么是三角形的高?怎样画三角形的高?和同伴一起交流.
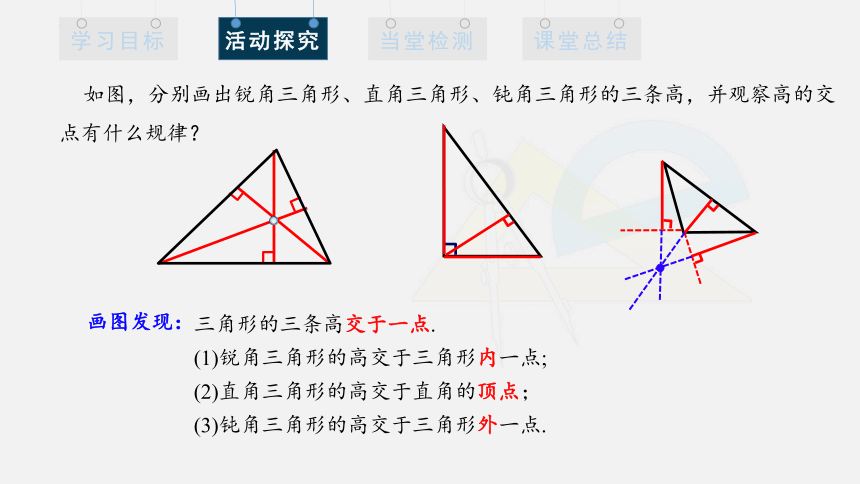
如图,分别画出锐角三角形、直角三角形、钝角三角形的三条高,并观察高的交点有什么规律?
画图发现:
三角形的三条高交于一点.
(1)锐角三角形的高交于三角形内一点;
(2)直角三角形的高交于直角的顶点;
(3)钝角三角形的高交于三角形外一点.
B
A
C
E
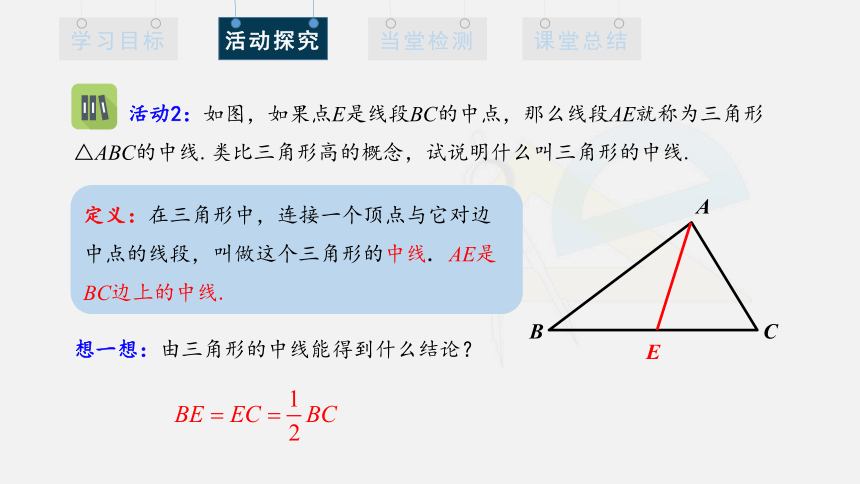
定义:在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线. AE是BC边上的中线.
活动2:如图,如果点E是线段BC的中点,那么线段AE就称为三角形△ABC的中线.类比三角形高的概念,试说明什么叫三角形的中线.
想一想:由三角形的中线能得到什么结论?
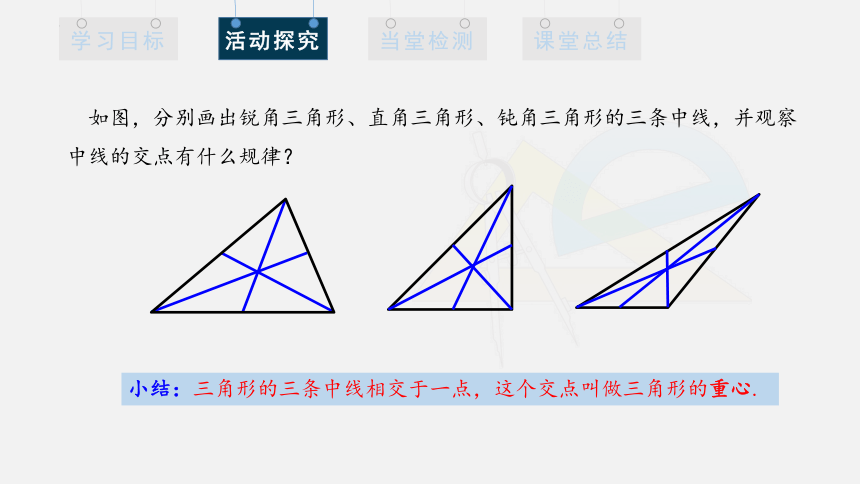
如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察中线的交点有什么规律?
小结:三角形的三条中线相交于一点,这个交点叫做三角形的重心.
A
C
B
∠1=∠2
1
2
D
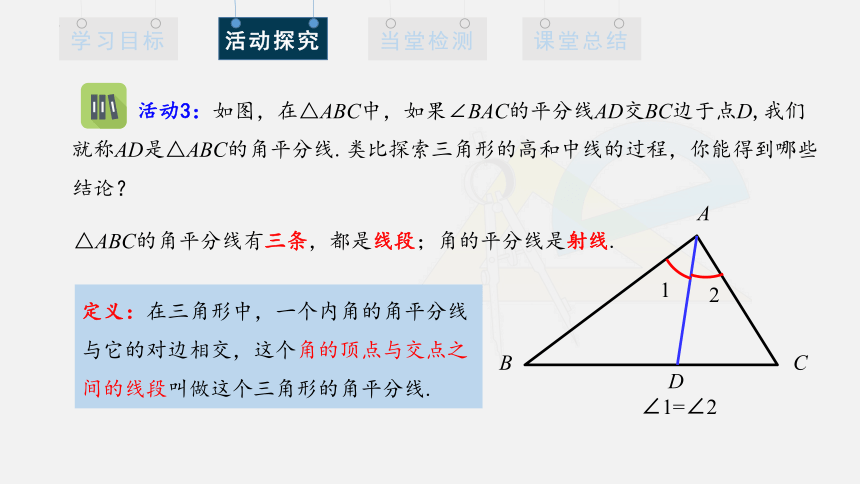
△ABC的角平分线有三条,都是线段;角的平分线是射线.
活动3:如图,在△ABC中,如果∠BAC的平分线AD交BC边于点D,我们就称AD是△ABC的角平分线.类比探索三角形的高和中线的过程,你能得到哪些结论?
定义:在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做这个三角形的角平分线.
请分别画出锐角三角形、直角三角形和钝角三角形这三个三角形的三条角平分线. 在每个三角形中,这三条角平分线之间有怎样的位置关系
小结:
三角形的三条角平分线交三角形内部于一点.
一个三角形中有几条高线 几条中线 几条角平分线 它们分别有什么关系
解:有三条高线、三条角平分线、三条中线.
一个三角形的三条高线所在的直线相交于一点;
一个三角形的三条中线相交于一点;
一个三角形的三条角平分线相交于一点.
练一练
任务二:能应用三角形的高、中线和角平分线的概念进行简单的计算.
(2)解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠DAC=∠BAD=30°.
∵CE是△ABC的高,∠BCE=40°,∴∠B=50°,
∴∠ADB=180°-∠B-∠BAD=180°-50°-30°=100°.
活动1:如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°.
(1)通过以上的信息,你能计算出哪些值?和同伴交流.
(2)求∠ADB的度数.
1.下列说法正确的是( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可能在三角形外
D.三角形的角平分线是射线
B
3.如图,AD、BE、CF是△ABC的三条角平分线,∠2=50°,∠ABC=50°,∠ACB=30°,则∠1=______, ∠3=_______, ∠4=_______.
50°
25°
15°
A
C
B
F
E
D
1
2
3
4
分析:根据三角形角平分线的性质可得:∠1=∠2,
∠ABC=2∠3,∠ACB=2∠4.
2.如图,AD是△ABC的中线,CE是△ACD的中线,S△AEC=3cm2,则S△ABC= .
12cm2
4.如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=82°,∠C=40°,求∠DAE的大小.
解: ∵ AD是△ABC的高,∴∠ADC=90°.
∵ ∠ADC+∠C+∠DAC=180°,
∴ ∠DAC=180°-(∠ADC+∠C )
=180°-90°-40°=50°.
∵AE是△ABC的角平分线,且∠BAC=82°,
∴∠CAE=41°,
∴∠DAE=∠DAC-∠CAE=50°-41°= 9°.
B
A
C
D
E
三角形
高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和
垂足之间的线段.
角平分线:在三角形中,一个内角的角平分线与它的对边相交,
这个角的顶点与交点之间的线段
中线:在三角形中,连接一个顶点与它对边中点的线段
第十一章 三角形
11.1 与三角形有关的线段
11.1.2 三角形的高、中线
与角平分线
1.掌握三角形的高,中线及角平分线的概念及其画法.
2.能应用三角形的高、中线和角平分线的概念进行简单的计算.
任务一:掌握三角形的高,中线及角平分线的概念及其画法.
定义:从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
A
B
C
D
注意:标明垂直的记号和垂足的字母.
活动1:什么是三角形的高?怎样画三角形的高?和同伴一起交流.
如图,分别画出锐角三角形、直角三角形、钝角三角形的三条高,并观察高的交点有什么规律?
画图发现:
三角形的三条高交于一点.
(1)锐角三角形的高交于三角形内一点;
(2)直角三角形的高交于直角的顶点;
(3)钝角三角形的高交于三角形外一点.
B
A
C
E
定义:在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线. AE是BC边上的中线.
活动2:如图,如果点E是线段BC的中点,那么线段AE就称为三角形△ABC的中线.类比三角形高的概念,试说明什么叫三角形的中线.
想一想:由三角形的中线能得到什么结论?
如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察中线的交点有什么规律?
小结:三角形的三条中线相交于一点,这个交点叫做三角形的重心.
A
C
B
∠1=∠2
1
2
D
△ABC的角平分线有三条,都是线段;角的平分线是射线.
活动3:如图,在△ABC中,如果∠BAC的平分线AD交BC边于点D,我们就称AD是△ABC的角平分线.类比探索三角形的高和中线的过程,你能得到哪些结论?
定义:在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做这个三角形的角平分线.
请分别画出锐角三角形、直角三角形和钝角三角形这三个三角形的三条角平分线. 在每个三角形中,这三条角平分线之间有怎样的位置关系
小结:
三角形的三条角平分线交三角形内部于一点.
一个三角形中有几条高线 几条中线 几条角平分线 它们分别有什么关系
解:有三条高线、三条角平分线、三条中线.
一个三角形的三条高线所在的直线相交于一点;
一个三角形的三条中线相交于一点;
一个三角形的三条角平分线相交于一点.
练一练
任务二:能应用三角形的高、中线和角平分线的概念进行简单的计算.
(2)解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠DAC=∠BAD=30°.
∵CE是△ABC的高,∠BCE=40°,∴∠B=50°,
∴∠ADB=180°-∠B-∠BAD=180°-50°-30°=100°.
活动1:如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°.
(1)通过以上的信息,你能计算出哪些值?和同伴交流.
(2)求∠ADB的度数.
1.下列说法正确的是( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可能在三角形外
D.三角形的角平分线是射线
B
3.如图,AD、BE、CF是△ABC的三条角平分线,∠2=50°,∠ABC=50°,∠ACB=30°,则∠1=______, ∠3=_______, ∠4=_______.
50°
25°
15°
A
C
B
F
E
D
1
2
3
4
分析:根据三角形角平分线的性质可得:∠1=∠2,
∠ABC=2∠3,∠ACB=2∠4.
2.如图,AD是△ABC的中线,CE是△ACD的中线,S△AEC=3cm2,则S△ABC= .
12cm2
4.如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=82°,∠C=40°,求∠DAE的大小.
解: ∵ AD是△ABC的高,∴∠ADC=90°.
∵ ∠ADC+∠C+∠DAC=180°,
∴ ∠DAC=180°-(∠ADC+∠C )
=180°-90°-40°=50°.
∵AE是△ABC的角平分线,且∠BAC=82°,
∴∠CAE=41°,
∴∠DAE=∠DAC-∠CAE=50°-41°= 9°.
B
A
C
D
E
三角形
高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和
垂足之间的线段.
角平分线:在三角形中,一个内角的角平分线与它的对边相交,
这个角的顶点与交点之间的线段
中线:在三角形中,连接一个顶点与它对边中点的线段
