6.1函数---2023-2024学年鲁教版七年级上册数学学历案(无答案)
文档属性
| 名称 | 6.1函数---2023-2024学年鲁教版七年级上册数学学历案(无答案) | 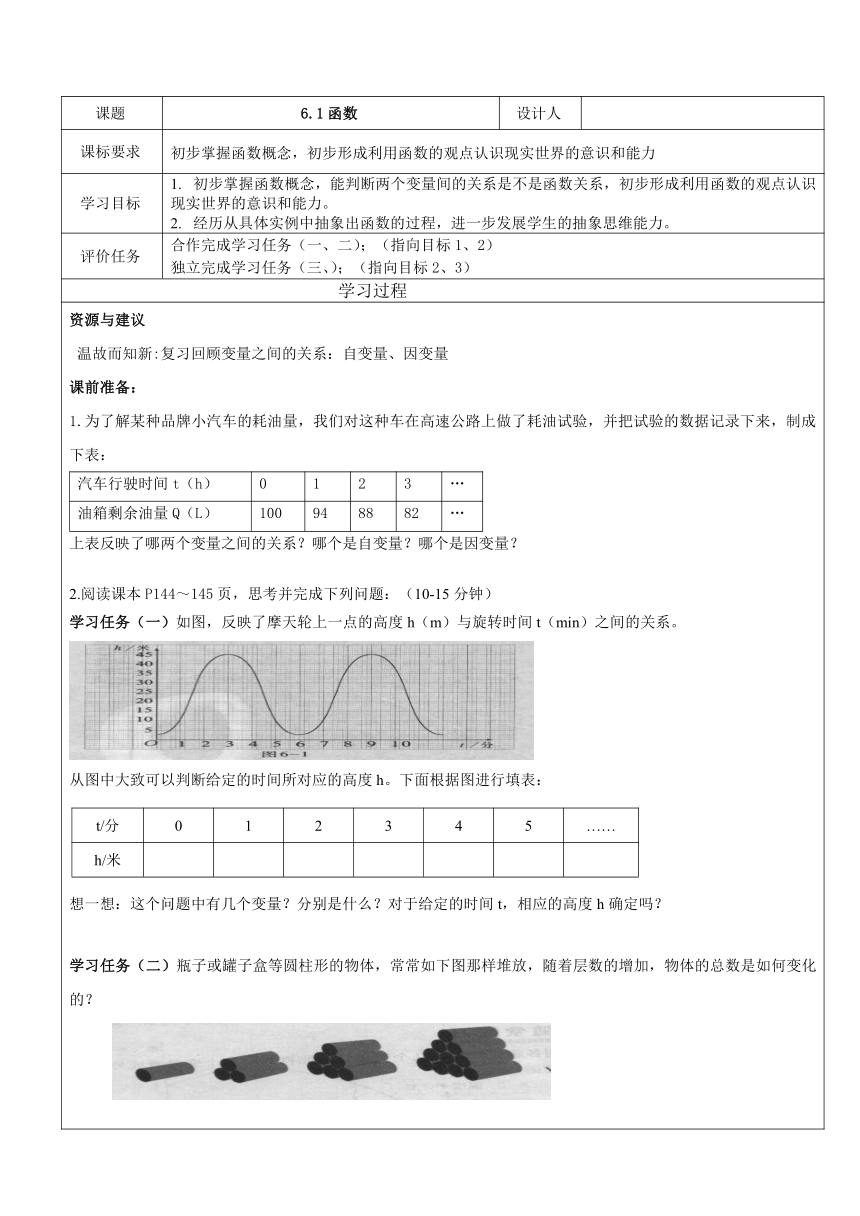 | |
| 格式 | docx | ||
| 文件大小 | 274.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 14:28:03 | ||
图片预览

文档简介
课题 6.1函数 设计人
课标要求 初步掌握函数概念,初步形成利用函数的观点认识现实世界的意识和能力
学习目标 初步掌握函数概念,能判断两个变量间的关系是不是函数关系,初步形成利用函数的观点认识现实世界的意识和能力。 经历从具体实例中抽象出函数的过程,进一步发展学生的抽象思维能力。
评价任务 合作完成学习任务(一、二);(指向目标1、2) 独立完成学习任务(三、);(指向目标2、3)
学习过程
资源与建议 温故而知新:复习回顾变量之间的关系:自变量、因变量 课前准备: 1.为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表: 汽车行驶时间t(h)0123…油箱剩余油量Q(L)100948882…
上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量? 2.阅读课本P144~145页,思考并完成下列问题:(10-15分钟) 学习任务(一)如图,反映了摩天轮上一点的高度h(m)与旋转时间t(min)之间的关系。 从图中大致可以判断给定的时间所对应的高度h。下面根据图进行填表: t/分012345……h/米
想一想:这个问题中有几个变量?分别是什么?对于给定的时间t,相应的高度h确定吗? 学习任务(二)瓶子或罐子盒等圆柱形的物体,常常如下图那样堆放,随着层数的增加,物体的总数是如何变化的? 层数n12345…物体总数y…
想一想:在这个问题中的变量有几个?分别是什么?对于给定的层数n,相应的物体总数y确定吗? 学习任务(三)一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零。因此,物理学中把-273℃作为热力学温度的零度。热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0。 (1)当t分别为-43,-27,0,18时,相应的热力学温度T是多少? 给定一个大于-273℃的t值,你都能求出相应的T值吗? 学习总结:1、如果在某个变化过程中有两个变量x和y,并且对于变量x的 , 变量y ,那么我们就称y是x的函数,其中x是 ,y是 2、表示函数的方法一般有: 巩固练习: 1、判断下列选项中的变量y是否为x的函数? ①y=2x ②y=x ③y=x ④y= ⑤=x 2、下列图形中的图像不表示y是x的函数的是( ) A.
B.
C.
D.
3、下列变量之间的关系中,具有函数关系的有( ) ①三角形的面积与底边 ②正方形的周长与面积 ③圆的面积与半径 ④y=中的y与x A.1个 B.2个 C.3个 D.4个 4、已知矩形的周长为24,设它的一边长为x,那么它的面积y与x之间的函数关系式为 。 5、已知等腰三角形的周长为20 cm,则腰长y(cm)与底边x(cm)的函数关系式为______,其中自变量x的取值范围是______。
学后反思
七年级数学 学历案 第___节/课第___课时
课标要求 初步掌握函数概念,初步形成利用函数的观点认识现实世界的意识和能力
学习目标 初步掌握函数概念,能判断两个变量间的关系是不是函数关系,初步形成利用函数的观点认识现实世界的意识和能力。 经历从具体实例中抽象出函数的过程,进一步发展学生的抽象思维能力。
评价任务 合作完成学习任务(一、二);(指向目标1、2) 独立完成学习任务(三、);(指向目标2、3)
学习过程
资源与建议 温故而知新:复习回顾变量之间的关系:自变量、因变量 课前准备: 1.为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表: 汽车行驶时间t(h)0123…油箱剩余油量Q(L)100948882…
上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量? 2.阅读课本P144~145页,思考并完成下列问题:(10-15分钟) 学习任务(一)如图,反映了摩天轮上一点的高度h(m)与旋转时间t(min)之间的关系。 从图中大致可以判断给定的时间所对应的高度h。下面根据图进行填表: t/分012345……h/米
想一想:这个问题中有几个变量?分别是什么?对于给定的时间t,相应的高度h确定吗? 学习任务(二)瓶子或罐子盒等圆柱形的物体,常常如下图那样堆放,随着层数的增加,物体的总数是如何变化的? 层数n12345…物体总数y…
想一想:在这个问题中的变量有几个?分别是什么?对于给定的层数n,相应的物体总数y确定吗? 学习任务(三)一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零。因此,物理学中把-273℃作为热力学温度的零度。热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0。 (1)当t分别为-43,-27,0,18时,相应的热力学温度T是多少? 给定一个大于-273℃的t值,你都能求出相应的T值吗? 学习总结:1、如果在某个变化过程中有两个变量x和y,并且对于变量x的 , 变量y ,那么我们就称y是x的函数,其中x是 ,y是 2、表示函数的方法一般有: 巩固练习: 1、判断下列选项中的变量y是否为x的函数? ①y=2x ②y=x ③y=x ④y= ⑤=x 2、下列图形中的图像不表示y是x的函数的是( ) A.
B.
C.
D.
3、下列变量之间的关系中,具有函数关系的有( ) ①三角形的面积与底边 ②正方形的周长与面积 ③圆的面积与半径 ④y=中的y与x A.1个 B.2个 C.3个 D.4个 4、已知矩形的周长为24,设它的一边长为x,那么它的面积y与x之间的函数关系式为 。 5、已知等腰三角形的周长为20 cm,则腰长y(cm)与底边x(cm)的函数关系式为______,其中自变量x的取值范围是______。
学后反思
七年级数学 学历案 第___节/课第___课时
