14.2.1平方差公式 培优练习 2023-2024学年人教版八年级数学上册(无答案)
文档属性
| 名称 | 14.2.1平方差公式 培优练习 2023-2024学年人教版八年级数学上册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 132.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 14:24:45 | ||
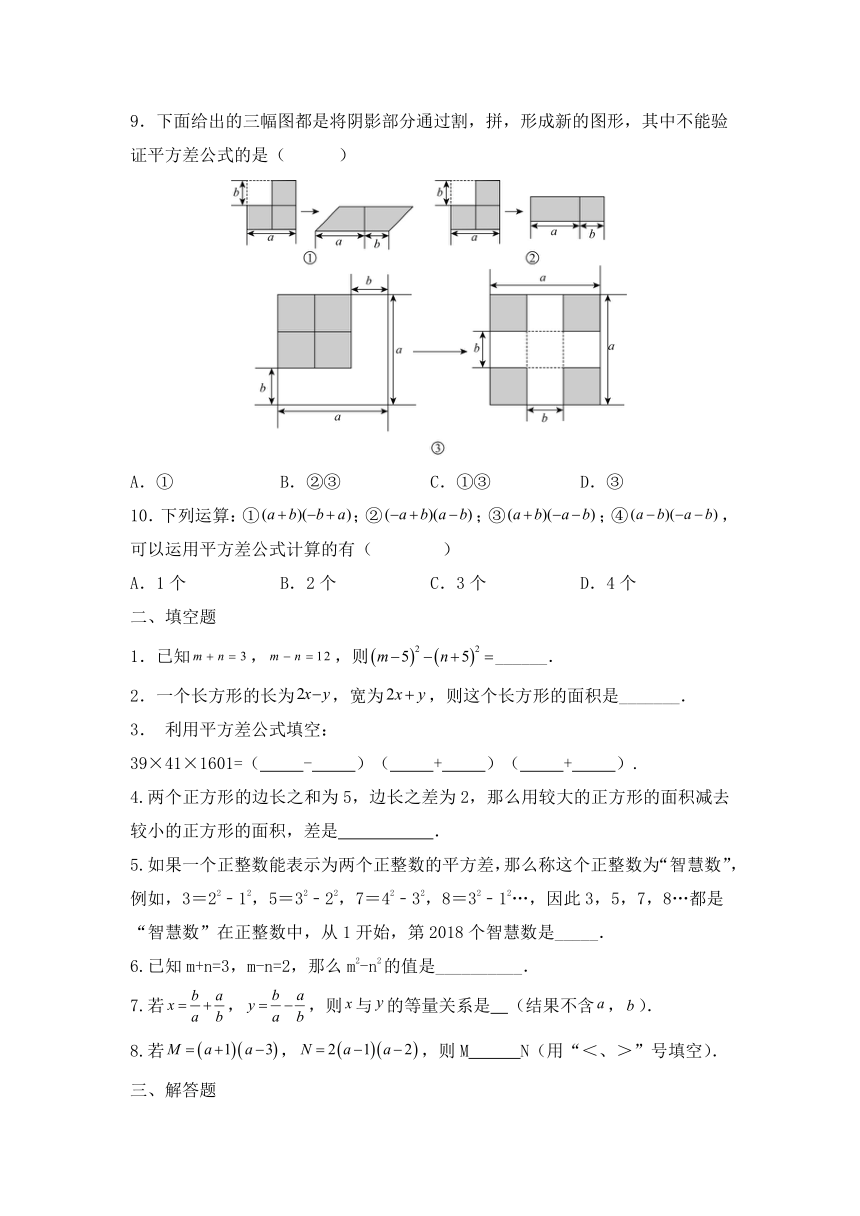
图片预览

文档简介
14.2.1平方差公式 培优练习
选择题
1.(3x+4y)(3x﹣4y)的结果是哪两个数的平方差( )
A.a,b B.x,y C.4y,3x D.3x,4y
2.下列运算中,可以运用平方差公式进行计算的是( )
A.(﹣2m+x)(﹣2x﹣m) B.(m+x)(﹣m+x)
C.(﹣m+x)(m﹣x) D.(m+x)(m﹣2x)
3.计算:(x﹣1)(x+1)(x2+1)﹣(x4+1)的结果为( )
A.0 B.2 C.﹣2 D.﹣2a4
4.三个连续奇数,中间一个是K,则这三个数的积为( )
A. B. C. D.
5.下列算式中,能连续两次用平方差公式计算的是
A. B.
C. D.
6.如果一个数等于两个连续奇数的平方差,那么我们称这个数为“幸福数”.下列数中为“幸福数”的是
A. B. C. D.
7.计算的结果是
A.2 B. C. D.1
8.在边长为a的正方形中剪掉一个边长为b的正方形[,如图(1)],然后将剩余部分拼成一个长方形[如图(2)].上述操作能验证的等式是( )
A. B.
C. D.
9.下面给出的三幅图都是将阴影部分通过割,拼,形成新的图形,其中不能验证平方差公式的是( )
A.① B.②③ C.①③ D.③
10.下列运算:①;②;③;④,可以运用平方差公式计算的有( )
A.1个 B.2个 C.3个 D.4个
填空题
1.已知,,则______.
2.一个长方形的长为,宽为,则这个长方形的面积是_______.
3. 利用平方差公式填空:
39×41×1601=( - )( + )( + ).
4.两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是 .
5.如果一个正整数能表示为两个正整数的平方差,那么称这个正整数为“智慧数”,例如,3=22﹣12,5=32﹣22,7=42﹣32,8=32﹣12…,因此3,5,7,8…都是“智慧数”在正整数中,从1开始,第2018个智慧数是_____.
6.已知m+n=3,m-n=2,那么m2-n2的值是__________.
7.若,,则与的等量关系是 (结果不含,).
8.若,,则M N(用“<、>”号填空).
三、解答题
1.计算:
(1);
(2);
;
(4);
;
(6).
2.已知与多项式M的差是,求M.
3.已知三角形的底边是,高是,求这个三角形的面积.若,,则这个三角形的面积是多少?
4.如图,有一个边长为2a(a>10)米的正方形池塘,为了创建文明农村,需在南北方向上扩大3米,东西方向上减少3米,从而得到一个长方形池塘.
(1)求改造后的长方形池塘的面积;
(2)改造后的长方形池塘的面积比原正方形池塘的面积变大还是变小了,请通过计算说明.
5.乘法公式的探究与应用:
(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分面积是 (写成两数平方差的形式)
(2)小颖将阴影部分裁下来,重新拼成一个长方形,如图乙,则长方形的长是 ,宽是 ,面积是 (写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到公式 (用式子表达)
(4)运用你所得到的公式计算:10.3×9.7
选择题
1.(3x+4y)(3x﹣4y)的结果是哪两个数的平方差( )
A.a,b B.x,y C.4y,3x D.3x,4y
2.下列运算中,可以运用平方差公式进行计算的是( )
A.(﹣2m+x)(﹣2x﹣m) B.(m+x)(﹣m+x)
C.(﹣m+x)(m﹣x) D.(m+x)(m﹣2x)
3.计算:(x﹣1)(x+1)(x2+1)﹣(x4+1)的结果为( )
A.0 B.2 C.﹣2 D.﹣2a4
4.三个连续奇数,中间一个是K,则这三个数的积为( )
A. B. C. D.
5.下列算式中,能连续两次用平方差公式计算的是
A. B.
C. D.
6.如果一个数等于两个连续奇数的平方差,那么我们称这个数为“幸福数”.下列数中为“幸福数”的是
A. B. C. D.
7.计算的结果是
A.2 B. C. D.1
8.在边长为a的正方形中剪掉一个边长为b的正方形[,如图(1)],然后将剩余部分拼成一个长方形[如图(2)].上述操作能验证的等式是( )
A. B.
C. D.
9.下面给出的三幅图都是将阴影部分通过割,拼,形成新的图形,其中不能验证平方差公式的是( )
A.① B.②③ C.①③ D.③
10.下列运算:①;②;③;④,可以运用平方差公式计算的有( )
A.1个 B.2个 C.3个 D.4个
填空题
1.已知,,则______.
2.一个长方形的长为,宽为,则这个长方形的面积是_______.
3. 利用平方差公式填空:
39×41×1601=( - )( + )( + ).
4.两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是 .
5.如果一个正整数能表示为两个正整数的平方差,那么称这个正整数为“智慧数”,例如,3=22﹣12,5=32﹣22,7=42﹣32,8=32﹣12…,因此3,5,7,8…都是“智慧数”在正整数中,从1开始,第2018个智慧数是_____.
6.已知m+n=3,m-n=2,那么m2-n2的值是__________.
7.若,,则与的等量关系是 (结果不含,).
8.若,,则M N(用“<、>”号填空).
三、解答题
1.计算:
(1);
(2);
;
(4);
;
(6).
2.已知与多项式M的差是,求M.
3.已知三角形的底边是,高是,求这个三角形的面积.若,,则这个三角形的面积是多少?
4.如图,有一个边长为2a(a>10)米的正方形池塘,为了创建文明农村,需在南北方向上扩大3米,东西方向上减少3米,从而得到一个长方形池塘.
(1)求改造后的长方形池塘的面积;
(2)改造后的长方形池塘的面积比原正方形池塘的面积变大还是变小了,请通过计算说明.
5.乘法公式的探究与应用:
(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分面积是 (写成两数平方差的形式)
(2)小颖将阴影部分裁下来,重新拼成一个长方形,如图乙,则长方形的长是 ,宽是 ,面积是 (写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到公式 (用式子表达)
(4)运用你所得到的公式计算:10.3×9.7
