24.2.1 点和圆的位置关系 强化练习 2023—2024学年人教版数学九年级上册(无答案)
文档属性
| 名称 | 24.2.1 点和圆的位置关系 强化练习 2023—2024学年人教版数学九年级上册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 163.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 14:04:26 | ||
图片预览


文档简介
24.2.1 点和圆的位置关系 强化练习
一、选择题
1.若一个三角形的三边长为6,8,10,则这个三角形外接圆的半径是( )
A.3 B.4 C.5 D.6
2.的半径为5,圆心的坐标为,点的坐标为,则点与的位置关系是( )
A.点在内 B.点在上
C.点在外 D.点在上或外
3.在同一平面内,点P到圆上的最大距离为5,最小距离为1,则此圆的半径为( )
A.3 B.4或6 C.2或3 D.6
4.用反证法证明“三角形的三个外角中至少有两个钝角”应假设( )
A.三个外角都为钝角
B.三个外角中两个为钝角
C.三个内角都为钝角
D.三个外角中只有一个或没有钝角
5.下列说法正确的是( )
A.弦是直径
B.平分弦的直径垂直弦
C.过三点A,B,C的圆有且只有一个
D.三角形的外心是三角形三边中垂线的交点
6.如图是一个含有3个正方形的相框,其中∠BCD=∠DEF=90°,AB=2,CD=3,EF=5,将它镶嵌在一个圆形的金属框上,使A,G, H三点刚好在金属框上,则该金属框的半径是( )
B.
C. D.
7.如图,在中,,,.以点为圆心,为半径作圆,当点在内且点在外时,的值可能是( )
A.2 B.3 C.4 D.5
8.如图,在平面直角坐标系中,△ABC为直角三角形,∠ABC=90°,AB⊥x轴,M为Rt△ABC的外心.若点A的坐标为(3,4),点M的坐标为(﹣1,1),则点B的坐标为( )
(3,﹣1) B.(3,﹣2)
C.(3,﹣3) D.(3,﹣4)
9.如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )
A.△ABE B.△ACF
C.△ABD D.△ADE
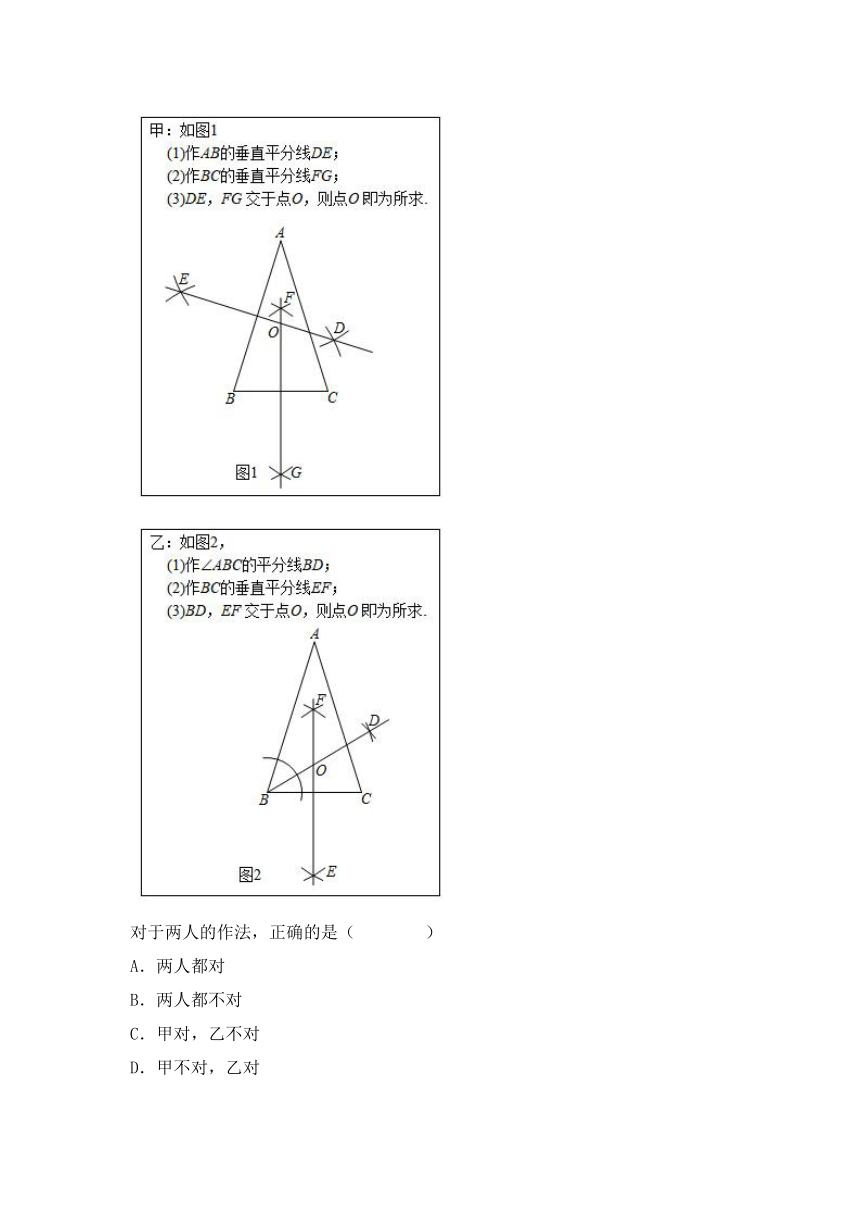
10.已知,在中,,求作的外心O,以下是甲、乙两同学的作法:
对于两人的作法,正确的是( )
两人都对
B.两人都不对
C.甲对,乙不对
D.甲不对,乙对
二、填空题
1.两直角边分别为6、8,那么的内接圆的半径为 .
2.若所在的平面内上有一点,它到上的点的最大距离是,最小距离是,则这个圆的半径为
3.如图,数轴上半径为1的⊙O从原点O开始以每秒1个单位的速度向右运动,同时,距原点右边7个单位有一点P以每秒2个单位的速度向左运动,经过 秒后,点P在⊙O上.
4.如图,抛物线与x轴交于点A,B,与y轴交于点C,动点P在射线上运动,作的外接圆,当圆心M落在该抛物线上时,的长为 .
5.如图,在马路上出现了如图所示的三角形塌陷,数据如图,工人师傅想用一个圆形井盖把它覆盖,那么井盖的最小半径是 cm.
6.如图,△ABC是⊙O的内接三角形,BC是直径,∠B=54°,∠BAC的平分线交⊙O于D,则∠ACD的度数是 .
解答题
1.如图,6*6的网格中,每个小正方形的边长为1.
(1)请画出将图中的△ABC绕着点M逆时针旋转90度得到的图形.
(2)用直尺和圆规画出△ABC的外接圆.(上述两题选作一题)
2.已知锐角△ABC是⊙O的内接三角形,OD⊥BC于点D.
(1)请借助无刻度的直尺,画出△ABC中∠BAC的平分线并说明理由;
(2)若∠BAC=60°,BC=,求OD旳长.
3.如图,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中劣弧AB上一点,延长DA至点E,使CE=CD.
(1)求证:∠ACE=∠BCD;
(2)若∠ACB=60°,试探究CD与AD+BD长度的大小关系,并证明你的结论.
4.如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,D为弧AC的中点,E是BA延长线上一点,∠DAE=105°.
(1)求∠CAD的度数;
(2)若⊙O的半径为4,求弧BC的长.
5.如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD.
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?若在,请用圆规作出这个圆,并说明理由;若不在,请说明不在的理由.(若作图,请保留作图痕迹)
一、选择题
1.若一个三角形的三边长为6,8,10,则这个三角形外接圆的半径是( )
A.3 B.4 C.5 D.6
2.的半径为5,圆心的坐标为,点的坐标为,则点与的位置关系是( )
A.点在内 B.点在上
C.点在外 D.点在上或外
3.在同一平面内,点P到圆上的最大距离为5,最小距离为1,则此圆的半径为( )
A.3 B.4或6 C.2或3 D.6
4.用反证法证明“三角形的三个外角中至少有两个钝角”应假设( )
A.三个外角都为钝角
B.三个外角中两个为钝角
C.三个内角都为钝角
D.三个外角中只有一个或没有钝角
5.下列说法正确的是( )
A.弦是直径
B.平分弦的直径垂直弦
C.过三点A,B,C的圆有且只有一个
D.三角形的外心是三角形三边中垂线的交点
6.如图是一个含有3个正方形的相框,其中∠BCD=∠DEF=90°,AB=2,CD=3,EF=5,将它镶嵌在一个圆形的金属框上,使A,G, H三点刚好在金属框上,则该金属框的半径是( )
B.
C. D.
7.如图,在中,,,.以点为圆心,为半径作圆,当点在内且点在外时,的值可能是( )
A.2 B.3 C.4 D.5
8.如图,在平面直角坐标系中,△ABC为直角三角形,∠ABC=90°,AB⊥x轴,M为Rt△ABC的外心.若点A的坐标为(3,4),点M的坐标为(﹣1,1),则点B的坐标为( )
(3,﹣1) B.(3,﹣2)
C.(3,﹣3) D.(3,﹣4)
9.如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )
A.△ABE B.△ACF
C.△ABD D.△ADE
10.已知,在中,,求作的外心O,以下是甲、乙两同学的作法:
对于两人的作法,正确的是( )
两人都对
B.两人都不对
C.甲对,乙不对
D.甲不对,乙对
二、填空题
1.两直角边分别为6、8,那么的内接圆的半径为 .
2.若所在的平面内上有一点,它到上的点的最大距离是,最小距离是,则这个圆的半径为
3.如图,数轴上半径为1的⊙O从原点O开始以每秒1个单位的速度向右运动,同时,距原点右边7个单位有一点P以每秒2个单位的速度向左运动,经过 秒后,点P在⊙O上.
4.如图,抛物线与x轴交于点A,B,与y轴交于点C,动点P在射线上运动,作的外接圆,当圆心M落在该抛物线上时,的长为 .
5.如图,在马路上出现了如图所示的三角形塌陷,数据如图,工人师傅想用一个圆形井盖把它覆盖,那么井盖的最小半径是 cm.
6.如图,△ABC是⊙O的内接三角形,BC是直径,∠B=54°,∠BAC的平分线交⊙O于D,则∠ACD的度数是 .
解答题
1.如图,6*6的网格中,每个小正方形的边长为1.
(1)请画出将图中的△ABC绕着点M逆时针旋转90度得到的图形.
(2)用直尺和圆规画出△ABC的外接圆.(上述两题选作一题)
2.已知锐角△ABC是⊙O的内接三角形,OD⊥BC于点D.
(1)请借助无刻度的直尺,画出△ABC中∠BAC的平分线并说明理由;
(2)若∠BAC=60°,BC=,求OD旳长.
3.如图,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中劣弧AB上一点,延长DA至点E,使CE=CD.
(1)求证:∠ACE=∠BCD;
(2)若∠ACB=60°,试探究CD与AD+BD长度的大小关系,并证明你的结论.
4.如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,D为弧AC的中点,E是BA延长线上一点,∠DAE=105°.
(1)求∠CAD的度数;
(2)若⊙O的半径为4,求弧BC的长.
5.如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD.
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?若在,请用圆规作出这个圆,并说明理由;若不在,请说明不在的理由.(若作图,请保留作图痕迹)
同课章节目录
