2023年吉林省长春市中考数学一轮复习学案:中点四边形(含答案)
文档属性
| 名称 | 2023年吉林省长春市中考数学一轮复习学案:中点四边形(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 129.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 00:00:00 | ||
图片预览

文档简介
吉林省长春市中考一轮复习中点四边形
知识点 中点四边形
1. 中点四边形:顺次连接四边形各边中点所得的四边形,我们称之为中点四边形.
如图,点E,F,G,H分别为四边形ABCD各边的中点,则四边形EFGH为中点四边形.
2. 常见中点四边形
①四边形的中点四边形为平行四边形;
②矩形的中点四边形为菱形;
③菱形的中点四边形为矩形;
④正方形的中点四边形为正方形;
⑤等腰梯形的中点四边形为菱形;
⑥对角线相等的中点四边形为菱形;
⑦对角线互相垂直的中点四边形为矩形.
对应训练
一、单选题
1.平行四边形ABCD中, ,则连接四边形ABCD四边中点所成的四边形是( )
A.平行四边形 B.菱形 C.矩形 D.正方形
2.顺次连接四边形ABCD各边中点E、F、G、H,若四边形EFGH为菱形,则四边形ABCD必须满足条件( )
A.四边形ABCD是平行四边形 B.四边形ABCD是矩形
C.四边形ABCD是菱形 D.AC=BD
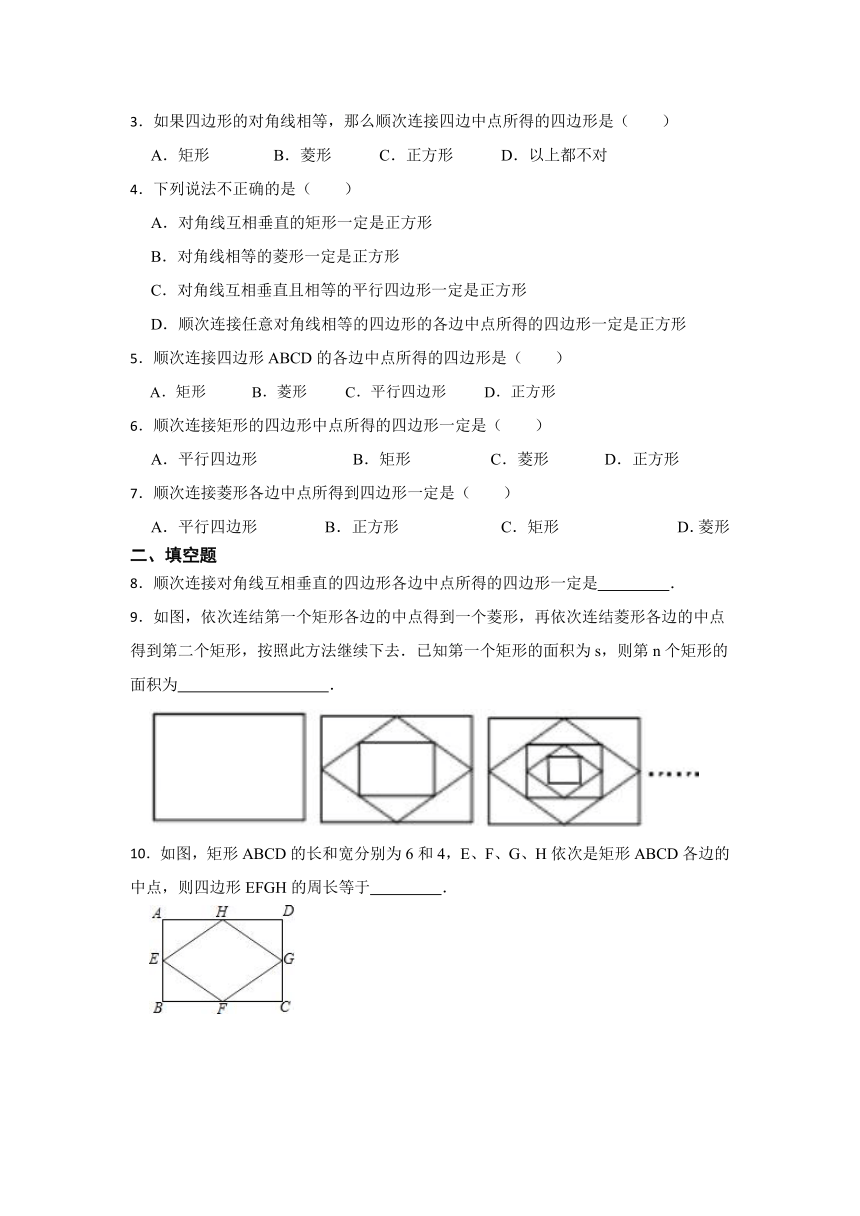
3.如果四边形的对角线相等,那么顺次连接四边中点所得的四边形是( )
A.矩形 B.菱形 C.正方形 D.以上都不对
4.下列说法不正确的是( )
A.对角线互相垂直的矩形一定是正方形
B.对角线相等的菱形一定是正方形
C.对角线互相垂直且相等的平行四边形一定是正方形
D.顺次连接任意对角线相等的四边形的各边中点所得的四边形一定是正方形
5.顺次连接四边形ABCD的各边中点所得的四边形是( )
A.矩形 B.菱形 C.平行四边形 D.正方形
6.顺次连接矩形的四边形中点所得的四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
7.顺次连接菱形各边中点所得到四边形一定是( )
A.平行四边形 B.正方形 C.矩形 D.菱形
二、填空题
8.顺次连接对角线互相垂直的四边形各边中点所得的四边形一定是 .
9.如图,依次连结第一个矩形各边的中点得到一个菱形,再依次连结菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为s,则第n个矩形的面积为 .
10.如图,矩形ABCD的长和宽分别为6和4,E、F、G、H依次是矩形ABCD各边的中点,则四边形EFGH的周长等于 .
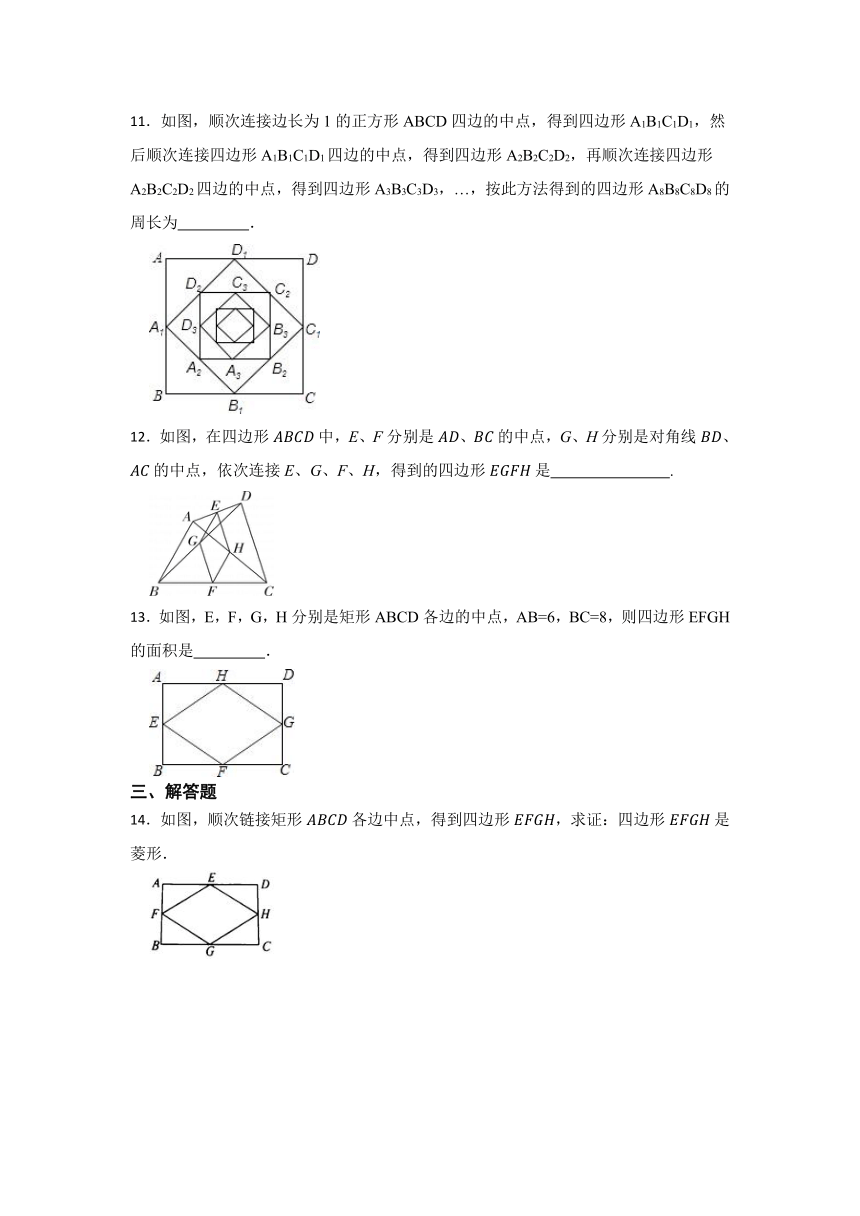
11.如图,顺次连接边长为1的正方形ABCD四边的中点,得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1四边的中点,得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点,得到四边形A3B3C3D3,…,按此方法得到的四边形A8B8C8D8的周长为 .
12.如图,在四边形中,E、F分别是、的中点,G、H分别是对角线、的中点,依次连接E、G、F、H,得到的四边形是 .
13.如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是 .
三、解答题
14.如图,顺次链接矩形各边中点,得到四边形,求证:四边形是菱形.
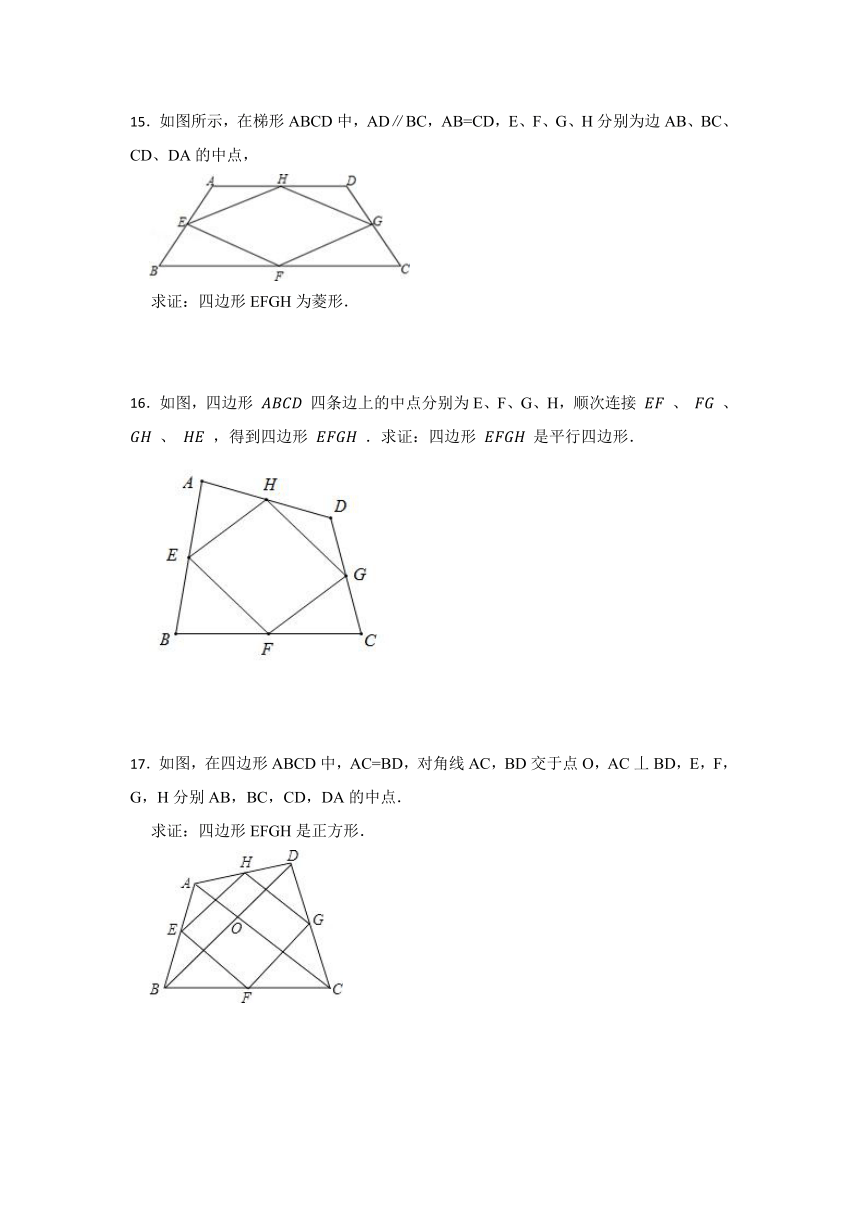
15.如图所示,在梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别为边AB、BC、CD、DA的中点,
求证:四边形EFGH为菱形.
16.如图,四边形 四条边上的中点分别为E、F、G、H,顺次连接 、 、 、 ,得到四边形 .求证:四边形 是平行四边形.
17.如图,在四边形ABCD中,AC=BD,对角线AC,BD交于点O,AC丄BD,E,F,G,H分别AB,BC,CD,DA的中点.
求证:四边形EFGH是正方形.
18.如图,在四边形ABCD中,对角线AC,BD相交于点O,且AC⊥BD,点E,F,G,H分别是AB,BC,CD,DA的中点,依次连接各边中点得到四边形EFGH,求证:四边形EFGH是矩形.
19.如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH,当四边形ABCD的对角线满足什么条件时,四边形EFGH是矩形,并说明理由.
答案
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】矩形
9.【答案】( s)2n﹣2
10.【答案】4
11.【答案】
12.【答案】平行四边形
13.【答案】24
14.【答案】证明:如图,连接,
四边形是矩形,
,
分别为的中点,
,
,
四边形是菱形.
15.【答案】 证明:连接AC、BD
∵梯形ABCD, AD∥BC,AB=CD
∴AC=BD
E、F、G、H分别为边AB、BC、CD、DA的中点,
HG,EF,EH分别是△ADC,△ABC,△ADB的中位线,
∴HG∥AC,HG=AC,EF∥AC,EF=AC,EH=BD
∴HG∥EF,HG=EF
∴四边形EFGH是平行四边形
∵EF=AC,EH=BD,AC=BD
∴EF=EH
∴四边形EFGH是菱形。
16.【答案】解:连接AC.
是DC的中点,H是AD的中点,
,且 ,
同理可知 ,且 ,
,且 ,
四边形 是平行四边形.
17.【答案】证明:在△ABC中,E、F分别是AB、BC的中点,
故可得:EF= AC,同理FG= BD,GH= AC,HE= BD,
在四边形ABCD中,AC=BD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
在△ABD中,E、H分别是AB、AD的中点,
则EH∥BD,
同理GH∥AC,
又∵AC⊥BD,
∴EH⊥HG,
∴四边形EFGH是正方形
18.【答案】证明:∵点E、F、G、H分别是边AB、BC、CD、DA的中点,
∴EF= AC,GH= AC,
∴EF=GH,同理EH=FG
∴四边形EFGH是平行四边形;
又∵对角线AC、BD互相垂直,
∴EF与FG垂直.
∴四边形EFGH是矩形
19.【答案】解:当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.理由如下:
如图,连接AC、BD.
∵E、H分别是AB、AD中点,
∴EH∥BD,EH=BD,
同理FG∥BD,FG=BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形,
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形.
知识点 中点四边形
1. 中点四边形:顺次连接四边形各边中点所得的四边形,我们称之为中点四边形.
如图,点E,F,G,H分别为四边形ABCD各边的中点,则四边形EFGH为中点四边形.
2. 常见中点四边形
①四边形的中点四边形为平行四边形;
②矩形的中点四边形为菱形;
③菱形的中点四边形为矩形;
④正方形的中点四边形为正方形;
⑤等腰梯形的中点四边形为菱形;
⑥对角线相等的中点四边形为菱形;
⑦对角线互相垂直的中点四边形为矩形.
对应训练
一、单选题
1.平行四边形ABCD中, ,则连接四边形ABCD四边中点所成的四边形是( )
A.平行四边形 B.菱形 C.矩形 D.正方形
2.顺次连接四边形ABCD各边中点E、F、G、H,若四边形EFGH为菱形,则四边形ABCD必须满足条件( )
A.四边形ABCD是平行四边形 B.四边形ABCD是矩形
C.四边形ABCD是菱形 D.AC=BD
3.如果四边形的对角线相等,那么顺次连接四边中点所得的四边形是( )
A.矩形 B.菱形 C.正方形 D.以上都不对
4.下列说法不正确的是( )
A.对角线互相垂直的矩形一定是正方形
B.对角线相等的菱形一定是正方形
C.对角线互相垂直且相等的平行四边形一定是正方形
D.顺次连接任意对角线相等的四边形的各边中点所得的四边形一定是正方形
5.顺次连接四边形ABCD的各边中点所得的四边形是( )
A.矩形 B.菱形 C.平行四边形 D.正方形
6.顺次连接矩形的四边形中点所得的四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
7.顺次连接菱形各边中点所得到四边形一定是( )
A.平行四边形 B.正方形 C.矩形 D.菱形
二、填空题
8.顺次连接对角线互相垂直的四边形各边中点所得的四边形一定是 .
9.如图,依次连结第一个矩形各边的中点得到一个菱形,再依次连结菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为s,则第n个矩形的面积为 .
10.如图,矩形ABCD的长和宽分别为6和4,E、F、G、H依次是矩形ABCD各边的中点,则四边形EFGH的周长等于 .
11.如图,顺次连接边长为1的正方形ABCD四边的中点,得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1四边的中点,得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点,得到四边形A3B3C3D3,…,按此方法得到的四边形A8B8C8D8的周长为 .
12.如图,在四边形中,E、F分别是、的中点,G、H分别是对角线、的中点,依次连接E、G、F、H,得到的四边形是 .
13.如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是 .
三、解答题
14.如图,顺次链接矩形各边中点,得到四边形,求证:四边形是菱形.
15.如图所示,在梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别为边AB、BC、CD、DA的中点,
求证:四边形EFGH为菱形.
16.如图,四边形 四条边上的中点分别为E、F、G、H,顺次连接 、 、 、 ,得到四边形 .求证:四边形 是平行四边形.
17.如图,在四边形ABCD中,AC=BD,对角线AC,BD交于点O,AC丄BD,E,F,G,H分别AB,BC,CD,DA的中点.
求证:四边形EFGH是正方形.
18.如图,在四边形ABCD中,对角线AC,BD相交于点O,且AC⊥BD,点E,F,G,H分别是AB,BC,CD,DA的中点,依次连接各边中点得到四边形EFGH,求证:四边形EFGH是矩形.
19.如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH,当四边形ABCD的对角线满足什么条件时,四边形EFGH是矩形,并说明理由.
答案
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】矩形
9.【答案】( s)2n﹣2
10.【答案】4
11.【答案】
12.【答案】平行四边形
13.【答案】24
14.【答案】证明:如图,连接,
四边形是矩形,
,
分别为的中点,
,
,
四边形是菱形.
15.【答案】 证明:连接AC、BD
∵梯形ABCD, AD∥BC,AB=CD
∴AC=BD
E、F、G、H分别为边AB、BC、CD、DA的中点,
HG,EF,EH分别是△ADC,△ABC,△ADB的中位线,
∴HG∥AC,HG=AC,EF∥AC,EF=AC,EH=BD
∴HG∥EF,HG=EF
∴四边形EFGH是平行四边形
∵EF=AC,EH=BD,AC=BD
∴EF=EH
∴四边形EFGH是菱形。
16.【答案】解:连接AC.
是DC的中点,H是AD的中点,
,且 ,
同理可知 ,且 ,
,且 ,
四边形 是平行四边形.
17.【答案】证明:在△ABC中,E、F分别是AB、BC的中点,
故可得:EF= AC,同理FG= BD,GH= AC,HE= BD,
在四边形ABCD中,AC=BD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
在△ABD中,E、H分别是AB、AD的中点,
则EH∥BD,
同理GH∥AC,
又∵AC⊥BD,
∴EH⊥HG,
∴四边形EFGH是正方形
18.【答案】证明:∵点E、F、G、H分别是边AB、BC、CD、DA的中点,
∴EF= AC,GH= AC,
∴EF=GH,同理EH=FG
∴四边形EFGH是平行四边形;
又∵对角线AC、BD互相垂直,
∴EF与FG垂直.
∴四边形EFGH是矩形
19.【答案】解:当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.理由如下:
如图,连接AC、BD.
∵E、H分别是AB、AD中点,
∴EH∥BD,EH=BD,
同理FG∥BD,FG=BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形,
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形.
同课章节目录
