苏科版八年级数学下册试题 第9章《中心对称图形—平行四边形》单元测试卷(含答案)
文档属性
| 名称 | 苏科版八年级数学下册试题 第9章《中心对称图形—平行四边形》单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 542.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 16:39:33 | ||
图片预览




文档简介
第9章《中心对称图形—平行四边形》单元测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列关于四边形的说法,正确的是( )
A.四个角相等的四边形是菱形
B.对角线互相垂直的四边形是矩形
C.有两边相等的平行四边形是菱形
D.两条对角线相等的菱形是矩形
2.如图,将△ABC绕着点B逆时针旋转45°后得到△A'BC′,若∠A=115°,∠C=35°,则∠A'BC的度数为( )
A.5° B.10° C.15° D.25°
3.建成具有全球影响力的“工程机械之都、汉文化名城”是徐州市2035远景目标,下列四个数字图形中,中心对称图形共有( )
A.1个 B.2个 C.3个 D.4个
4.如图,线段AB与线段CD关于点P对称,若点A(a,b)、B(5,1)、D(﹣3,﹣1),则点C的坐标为( )
A.(﹣a,﹣b) B.(﹣a+2,﹣b)
C.(﹣a﹣1,﹣b+1) D.(﹣a+1,﹣b﹣1)
5.如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O.下列条件:①AD∥BC,②AB=CD,③AD=BC,④∠ADC=∠ABC,⑤BO=DO,⑥∠DBA=∠CAB.若添加其中一个,可得到该四边形是平行四边形,则添加的条件可以是( )
A.①②③⑤ B.①②④⑤ C.①②④⑥ D.①③④⑥
6.如图,菱形ABCD和菱形EFGH,∠A=∠E,它们的面积分别为9cm2和64cm2,CD落在EF上,若△BCF的面积为4cm2,则△BDH的面积是( )
A.8cm2 B.8.5cm2 C.9cm2 D.9.5cm2
7.如图,在四边形ABCD中,AB∥CD,∠C=90°,AB=8,AD=CD=5,点M、N分别为BC、AB上的动点(含端点),E、F分别为DM、MN的中点,则EF长度的最小值为( )
A.3 B.2.5 C.2 D.1
8.如图,在矩形ABCD中,E是AB的中点,动点F从点B出发,沿BC运动到点C时停止,以EF为边作 EFGH,且点G、H分别在CD、AD上.在动点F运动的过程中, EFGH的面积( )
A.逐渐增大 B.逐渐减小
C.不变 D.先增大,再减小
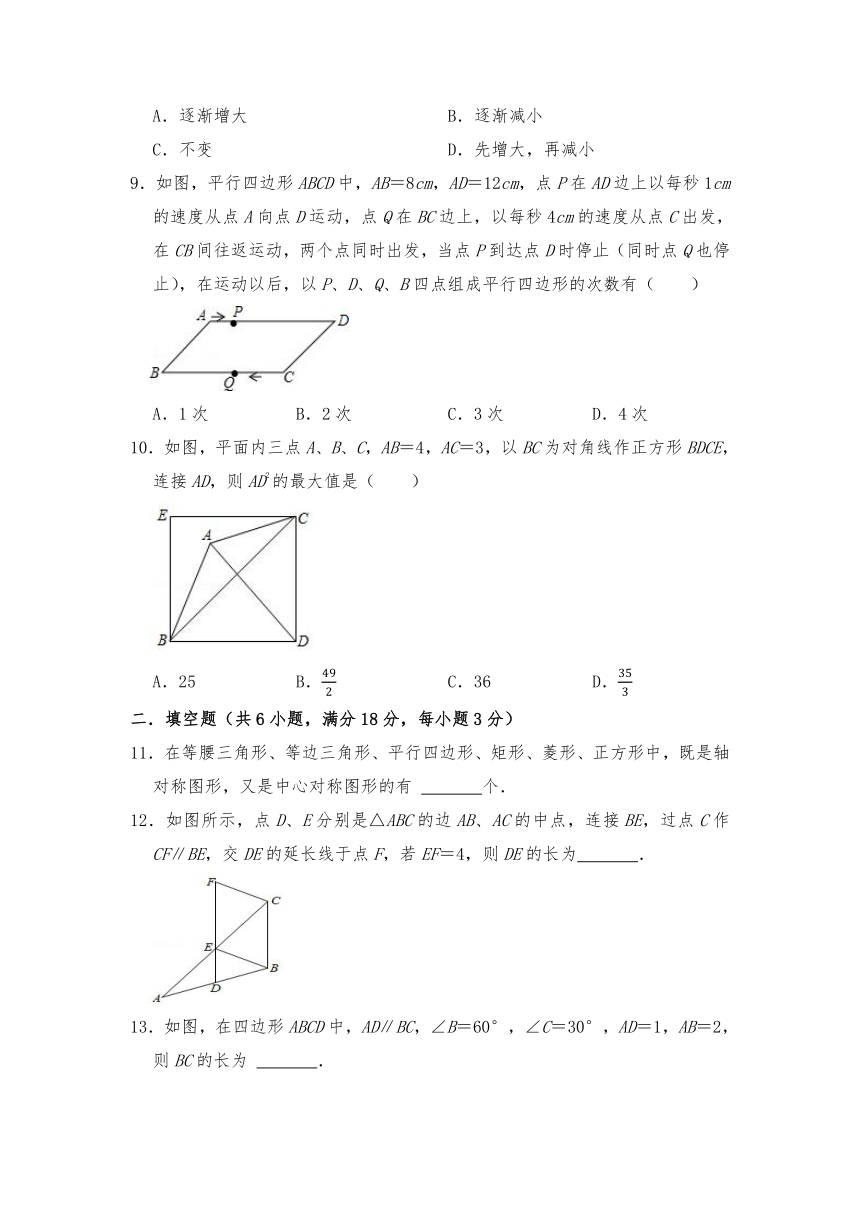
9.如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )
A.1次 B.2次 C.3次 D.4次
10.如图,平面内三点A、B、C,AB=4,AC=3,以BC为对角线作正方形BDCE,连接AD,则AD2的最大值是( )
A.25 B. C.36 D.
二.填空题(共6小题,满分18分,每小题3分)
11.在等腰三角形、等边三角形、平行四边形、矩形、菱形、正方形中,既是轴对称图形,又是中心对称图形的有 个.
12.如图所示,点D、E分别是△ABC的边AB、AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若EF=4,则DE的长为 .
13.如图,在四边形ABCD中,AD∥BC,∠B=60°,∠C=30°,AD=1,AB=2,则BC的长为 .
14.如图,菱形ABCD的面积为120,正方形DEBF的面积为50,则菱形ABCD的周长为 .
15.如图,已知∠ACB=∠ADB=90°,BD=AD,AC=3,BC=4,则线段CD的长为 .
16.如图,矩形ABCD的边AB,BC=3,E为AB上一点,且AE=1,F为AD边上的一个动点,连接EF,若以EF为边向右侧作等腰直角三角形EFG,EF=EG,连接CG,则CG的最小值为 .
三.解答题(共7小题,满分52分)
17.(6分)如图,在方格中,正方形被分成4个全等的直角三角形,请你用这4个全等的直角三角形在下面三个方格中分别重新拼接成一个新的四边形,要求新的四边形是中心对称图形.
18.(6分)如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.
(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
19.(6分)如图,在△ABC中,E、F分别是AB、AC的中点,延长EF交△ABC的外角∠ACD的平分线于点G.AG与CG有怎样的位置关系?证明你的结论.
20.(8分)拿出平行四边形的活动框架,对角线是两根橡皮筋.如果把DC沿CB方向平行移动, ABCD的边、内角、对角线都随着变化.当平移DC使BC=AB时:
(1) ABCD四条边的大小有什么关系?结合图形说明理由.
(2)对角线AC、BD的位置有什么关系?结合图形说明理由.
21.(8分)在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.
(1)若G,H分别是AB,DC中点,试说明:四边形EGFH为平行四边形;
(2)在(1)的条件下,当t为何值时,四边形EGFH为矩形.
22.(10分)在平行四边形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
23.(8分)(1)如图①,在正方形ABCD中,E、F分别是BC、DC上的点,且∠EAF=45°,连接EF,探究BE、DF、EF之间的数量关系,并说明理由;
(2)如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、DC上的点,且∠EAF∠BAD,此时(1)中的结论是否仍然成立?请说明理由.
答案
一.选择题
D.C.C.B.B.B.C.C.C.B.
二.填空题
11.3.
12.2.
13.5.
14.52.
15..
16.2.5.
三.解答题
17.解:如图所示:
18.(1)证明:如图:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BCF,
在△ADE与△CBF中,
,
∴△ADE≌△CBF(AAS),
∴AE=CF;
(2)证明:∵∠1=∠2,
∴∠DEF=∠BFE,
∴DE∥BF.
由(1)知△ADE≌△CBF,
∴DE=BF,
∴四边形EBFD是平行四边形.
19.解:AG⊥CG,
理由:∵E、F分别是AB、AC的中点,
∴EF是△ABC的中位线,AF=CF,
∴EF∥BC,
∴∠FGC=∠GCD.
∵CG平分∠ACD,
∴∠FCG=∠GCD,
∴∠FCG=∠FGC,
∴FG=FC.
又∵AF=CF,
∴FG是△ACG中AC边上的中线,且FGAC,
∴△AGC是直角三角形,
∴AG⊥CG.
20.解:(1) ABCD四条边相等,
理由:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴BC=AB,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形,
∴ ABCD四条边相等;
(2)对角线AC、BD互相垂直,
理由:由(1)得:四边形ABCD是菱形,
∴AC⊥BD,
∴对角线AC、BD互相垂直.
21.(1)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴∠GAF=∠HCE,
∵G、H分别是AB、DC的中点,
∴AG=BG,CH=DH,
∴AG=CH,
∵AE=CF,
∴AF=CE,
在△AFG与△CEH中,
∴△AFG≌△CEH(SAS),
∴GF=HE,
同理:GE=HF,
∴四边形EGFH是平行四边形.
(2)解:∵四边形ABCD是矩形,
∴∠B=90°,
∴AC5,
由(2)可知四边形EGFH是平行四边形,
连接GH,
∵点G、H分别是矩形ABCD的边AB、DC的中点,
∴AG=DH,AG∥DH,
∴四边形AGHD是平行四边形,
∴GH=BC=4,
∴当EF=GH=4时,四边形EGFH是矩形,分两种情况:
①如图1,AE=CF=t,
则EF=5﹣2t=4,
解得:t=0.5;
②AE=CF=t,EF=5﹣2(5﹣t)=4,
解得:t=4.5;
综上所述,当t为0.5或4.5时,四边形EGFH为矩形.
22.解:(1)证明:∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形.
(2)如图,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形,
∴∠BDM=45°;
(3)∠BDG=60°,
延长AB、FG交于H,连接HD.
∵AD∥GF,AB∥DF,
∴四边形AHFD为平行四边形,
∵∠ABC=120°,AF平分∠BAD,
∴∠DAF=30°,∠ADC=120°,∠DFA=30°,
∴△DAF为等腰三角形,
∴AD=DF,
∴平行四边形AHFD为菱形,
∴△ADH,△DHF为全等的等边三角形,
∴DH=DF,∠BHD=∠GFD=60°,
∵FG=CE,CE=CF,CF=BH,
∴BH=GF,
在△BHD与△GFD中,
∵,
∴△BHD≌△GFD(SAS),
∴∠BDH=∠GDF
∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°.
23.解:(1)如图1,
EF=BE+DF,理由如下:
延长CB到M,使得BM=DF,连接AM,
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABM=90°,
又∵BM=DF,
∴△ADF≌△ABM(SAS),
∴AF=AM,∠1=∠2,
∵∠EAF=45°,
∴∠1+∠3=45°,
∴∠2+∠3=∠MAE=45°=∠EAF,
又∵AE=AE,
∴△EAM≌△EAF(SAS),
∴EF=EM=BE+BM,
又∵BM=DF,
∴EF=EB+DF,
(2)如图2,
EF=BE+DF,仍然成立,理由如下:
延长CB到M,使得BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠4=180°,
∴∠D=∠4,
又∵AB=AD,BM=DF,
∴△ADF≌△ABM(SAS),
∴AF=AM,∠1=∠2,
∵,
∴∠1+∠3=∠EAF,
∴∠MAE=∠2+∠3=∠EAF,
又∵AE=AE,
∴△EAM≌△EAF(SAS),
∴EF=EM=BE+BM,
又∵BM=DF,
∴EF=EB+DF.
一.选择题(共10小题,满分30分,每小题3分)
1.下列关于四边形的说法,正确的是( )
A.四个角相等的四边形是菱形
B.对角线互相垂直的四边形是矩形
C.有两边相等的平行四边形是菱形
D.两条对角线相等的菱形是矩形
2.如图,将△ABC绕着点B逆时针旋转45°后得到△A'BC′,若∠A=115°,∠C=35°,则∠A'BC的度数为( )
A.5° B.10° C.15° D.25°
3.建成具有全球影响力的“工程机械之都、汉文化名城”是徐州市2035远景目标,下列四个数字图形中,中心对称图形共有( )
A.1个 B.2个 C.3个 D.4个
4.如图,线段AB与线段CD关于点P对称,若点A(a,b)、B(5,1)、D(﹣3,﹣1),则点C的坐标为( )
A.(﹣a,﹣b) B.(﹣a+2,﹣b)
C.(﹣a﹣1,﹣b+1) D.(﹣a+1,﹣b﹣1)
5.如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O.下列条件:①AD∥BC,②AB=CD,③AD=BC,④∠ADC=∠ABC,⑤BO=DO,⑥∠DBA=∠CAB.若添加其中一个,可得到该四边形是平行四边形,则添加的条件可以是( )
A.①②③⑤ B.①②④⑤ C.①②④⑥ D.①③④⑥
6.如图,菱形ABCD和菱形EFGH,∠A=∠E,它们的面积分别为9cm2和64cm2,CD落在EF上,若△BCF的面积为4cm2,则△BDH的面积是( )
A.8cm2 B.8.5cm2 C.9cm2 D.9.5cm2
7.如图,在四边形ABCD中,AB∥CD,∠C=90°,AB=8,AD=CD=5,点M、N分别为BC、AB上的动点(含端点),E、F分别为DM、MN的中点,则EF长度的最小值为( )
A.3 B.2.5 C.2 D.1
8.如图,在矩形ABCD中,E是AB的中点,动点F从点B出发,沿BC运动到点C时停止,以EF为边作 EFGH,且点G、H分别在CD、AD上.在动点F运动的过程中, EFGH的面积( )
A.逐渐增大 B.逐渐减小
C.不变 D.先增大,再减小
9.如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )
A.1次 B.2次 C.3次 D.4次
10.如图,平面内三点A、B、C,AB=4,AC=3,以BC为对角线作正方形BDCE,连接AD,则AD2的最大值是( )
A.25 B. C.36 D.
二.填空题(共6小题,满分18分,每小题3分)
11.在等腰三角形、等边三角形、平行四边形、矩形、菱形、正方形中,既是轴对称图形,又是中心对称图形的有 个.
12.如图所示,点D、E分别是△ABC的边AB、AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若EF=4,则DE的长为 .
13.如图,在四边形ABCD中,AD∥BC,∠B=60°,∠C=30°,AD=1,AB=2,则BC的长为 .
14.如图,菱形ABCD的面积为120,正方形DEBF的面积为50,则菱形ABCD的周长为 .
15.如图,已知∠ACB=∠ADB=90°,BD=AD,AC=3,BC=4,则线段CD的长为 .
16.如图,矩形ABCD的边AB,BC=3,E为AB上一点,且AE=1,F为AD边上的一个动点,连接EF,若以EF为边向右侧作等腰直角三角形EFG,EF=EG,连接CG,则CG的最小值为 .
三.解答题(共7小题,满分52分)
17.(6分)如图,在方格中,正方形被分成4个全等的直角三角形,请你用这4个全等的直角三角形在下面三个方格中分别重新拼接成一个新的四边形,要求新的四边形是中心对称图形.
18.(6分)如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.
(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
19.(6分)如图,在△ABC中,E、F分别是AB、AC的中点,延长EF交△ABC的外角∠ACD的平分线于点G.AG与CG有怎样的位置关系?证明你的结论.
20.(8分)拿出平行四边形的活动框架,对角线是两根橡皮筋.如果把DC沿CB方向平行移动, ABCD的边、内角、对角线都随着变化.当平移DC使BC=AB时:
(1) ABCD四条边的大小有什么关系?结合图形说明理由.
(2)对角线AC、BD的位置有什么关系?结合图形说明理由.
21.(8分)在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.
(1)若G,H分别是AB,DC中点,试说明:四边形EGFH为平行四边形;
(2)在(1)的条件下,当t为何值时,四边形EGFH为矩形.
22.(10分)在平行四边形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
23.(8分)(1)如图①,在正方形ABCD中,E、F分别是BC、DC上的点,且∠EAF=45°,连接EF,探究BE、DF、EF之间的数量关系,并说明理由;
(2)如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、DC上的点,且∠EAF∠BAD,此时(1)中的结论是否仍然成立?请说明理由.
答案
一.选择题
D.C.C.B.B.B.C.C.C.B.
二.填空题
11.3.
12.2.
13.5.
14.52.
15..
16.2.5.
三.解答题
17.解:如图所示:
18.(1)证明:如图:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BCF,
在△ADE与△CBF中,
,
∴△ADE≌△CBF(AAS),
∴AE=CF;
(2)证明:∵∠1=∠2,
∴∠DEF=∠BFE,
∴DE∥BF.
由(1)知△ADE≌△CBF,
∴DE=BF,
∴四边形EBFD是平行四边形.
19.解:AG⊥CG,
理由:∵E、F分别是AB、AC的中点,
∴EF是△ABC的中位线,AF=CF,
∴EF∥BC,
∴∠FGC=∠GCD.
∵CG平分∠ACD,
∴∠FCG=∠GCD,
∴∠FCG=∠FGC,
∴FG=FC.
又∵AF=CF,
∴FG是△ACG中AC边上的中线,且FGAC,
∴△AGC是直角三角形,
∴AG⊥CG.
20.解:(1) ABCD四条边相等,
理由:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴BC=AB,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形,
∴ ABCD四条边相等;
(2)对角线AC、BD互相垂直,
理由:由(1)得:四边形ABCD是菱形,
∴AC⊥BD,
∴对角线AC、BD互相垂直.
21.(1)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴∠GAF=∠HCE,
∵G、H分别是AB、DC的中点,
∴AG=BG,CH=DH,
∴AG=CH,
∵AE=CF,
∴AF=CE,
在△AFG与△CEH中,
∴△AFG≌△CEH(SAS),
∴GF=HE,
同理:GE=HF,
∴四边形EGFH是平行四边形.
(2)解:∵四边形ABCD是矩形,
∴∠B=90°,
∴AC5,
由(2)可知四边形EGFH是平行四边形,
连接GH,
∵点G、H分别是矩形ABCD的边AB、DC的中点,
∴AG=DH,AG∥DH,
∴四边形AGHD是平行四边形,
∴GH=BC=4,
∴当EF=GH=4时,四边形EGFH是矩形,分两种情况:
①如图1,AE=CF=t,
则EF=5﹣2t=4,
解得:t=0.5;
②AE=CF=t,EF=5﹣2(5﹣t)=4,
解得:t=4.5;
综上所述,当t为0.5或4.5时,四边形EGFH为矩形.
22.解:(1)证明:∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形.
(2)如图,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形,
∴∠BDM=45°;
(3)∠BDG=60°,
延长AB、FG交于H,连接HD.
∵AD∥GF,AB∥DF,
∴四边形AHFD为平行四边形,
∵∠ABC=120°,AF平分∠BAD,
∴∠DAF=30°,∠ADC=120°,∠DFA=30°,
∴△DAF为等腰三角形,
∴AD=DF,
∴平行四边形AHFD为菱形,
∴△ADH,△DHF为全等的等边三角形,
∴DH=DF,∠BHD=∠GFD=60°,
∵FG=CE,CE=CF,CF=BH,
∴BH=GF,
在△BHD与△GFD中,
∵,
∴△BHD≌△GFD(SAS),
∴∠BDH=∠GDF
∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°.
23.解:(1)如图1,
EF=BE+DF,理由如下:
延长CB到M,使得BM=DF,连接AM,
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABM=90°,
又∵BM=DF,
∴△ADF≌△ABM(SAS),
∴AF=AM,∠1=∠2,
∵∠EAF=45°,
∴∠1+∠3=45°,
∴∠2+∠3=∠MAE=45°=∠EAF,
又∵AE=AE,
∴△EAM≌△EAF(SAS),
∴EF=EM=BE+BM,
又∵BM=DF,
∴EF=EB+DF,
(2)如图2,
EF=BE+DF,仍然成立,理由如下:
延长CB到M,使得BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠4=180°,
∴∠D=∠4,
又∵AB=AD,BM=DF,
∴△ADF≌△ABM(SAS),
∴AF=AM,∠1=∠2,
∵,
∴∠1+∠3=∠EAF,
∴∠MAE=∠2+∠3=∠EAF,
又∵AE=AE,
∴△EAM≌△EAF(SAS),
∴EF=EM=BE+BM,
又∵BM=DF,
∴EF=EB+DF.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
