九年级数学下册试题 6.7 用相似三角形解决问题 苏科版(含答案)
文档属性
| 名称 | 九年级数学下册试题 6.7 用相似三角形解决问题 苏科版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 262.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 18:01:06 | ||
图片预览



文档简介
6.7用相似三角形解决问题
一.选择题
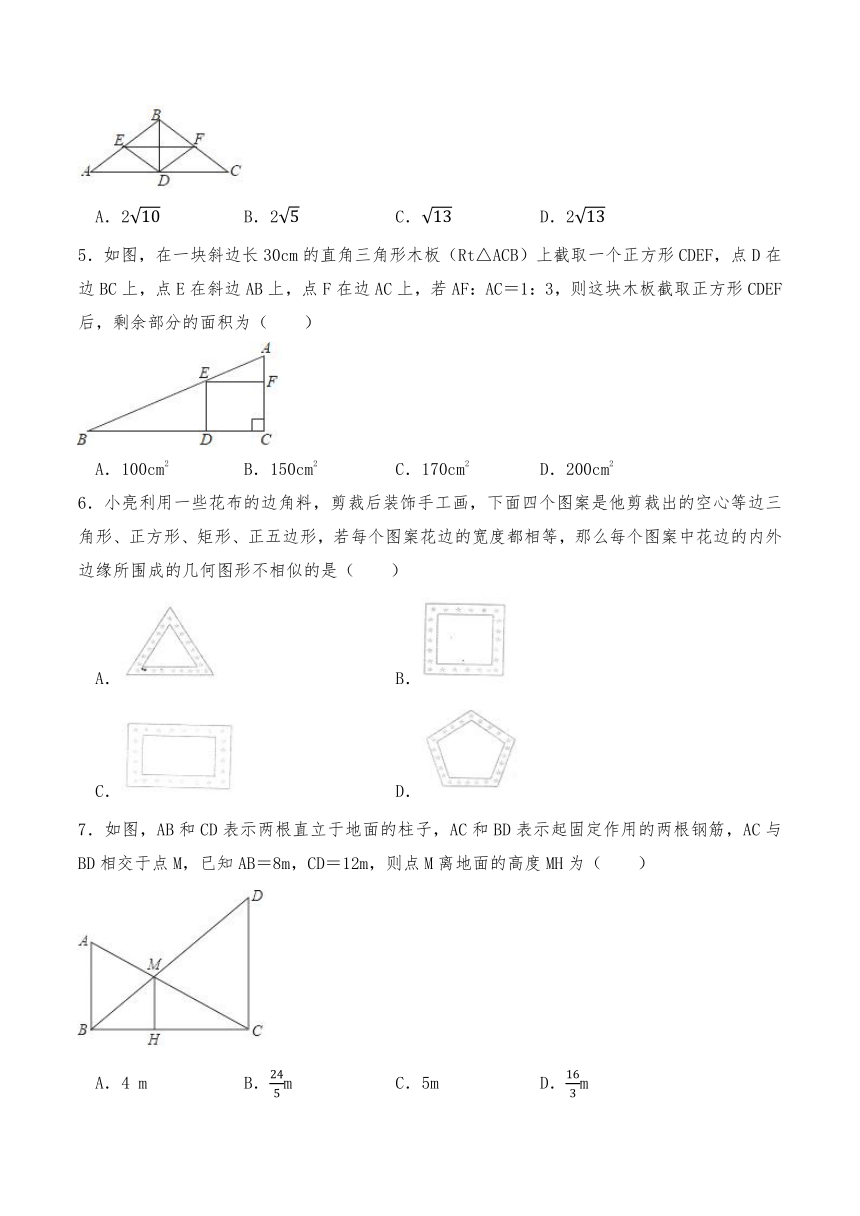
1.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5m,测得AB=1.2m,BC=12.8m,则建筑物CD的高是( )
A.17.5m B.17m C.16.5m D.18m
2.数学兴趣小组的同学们来到宝安区海淀广场,设计用手电来测量广场附近某大厦CD的高度,如图,点P处放一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1米,BP=1.5米,PD=48米,那么该大厦的高度约为( )
A.32米 B.28米 C.24米 D.16米
3.如图,某同学拿着一把12cm长的尺子,站在距电线杆30m的位置,把手臂向前伸直,将尺子竖直,看到尺子恰好遮住电线杆,已知臂长60cm,则电线杆的高度是( )
A.2.4m B.24m C.0.6m D.6m
4.如图为一座房屋屋架结构示意图,已知屋檐AB=BC,横梁EF∥AC,点E为AB的中点,且BD⊥EF,屋架高BD=4m,横梁AC=12m,则支架DF长为( )
A.2 B.2 C. D.2
5.如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A.100cm2 B.150cm2 C.170cm2 D.200cm2
6.小亮利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是他剪裁出的空心等边三角形、正方形、矩形、正五边形,若每个图案花边的宽度都相等,那么每个图案中花边的内外边缘所围成的几何图形不相似的是( )
A. B.
C. D.
7.如图,AB和CD表示两根直立于地面的柱子,AC和BD表示起固定作用的两根钢筋,AC与BD相交于点M,已知AB=8m,CD=12m,则点M离地面的高度MH为( )
A.4 m B.m C.5m D.m
8.如图,有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着底边BC修一座底面是矩形DEFG的大楼,则这座大楼的地基面积最大值是( )
A.1000米2 B.2000米2 C.3000米2 D.4000米2
9.如图,有一块三角形余料ABC,BC=120mm,高线AD=80mm,要把它加工成一个矩形零件,使矩形的一边在BC上,点P,M分别在AB,AC上,若满足PM:PQ=3:2,则PM的长为( )
A.60mm B.mm C.20mm D.mm
10.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中第九卷《勾股》章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”
译文:“今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)
你的计算结果是:出南门几何步而见木( )
A.300步 B.315 步 C.400 步 D.415步
11.相邻两根电杆都用钢索在地面上固定,如图,一根电杆钢索系在离地面4米处,另一根电杆钢索系在离地面6米处,则中间两根钢索相交处点P离地面( )
A.2.4米 B.8米
C.3米 D.必须知道两根电线杆的距离才能求出点P离地面距离
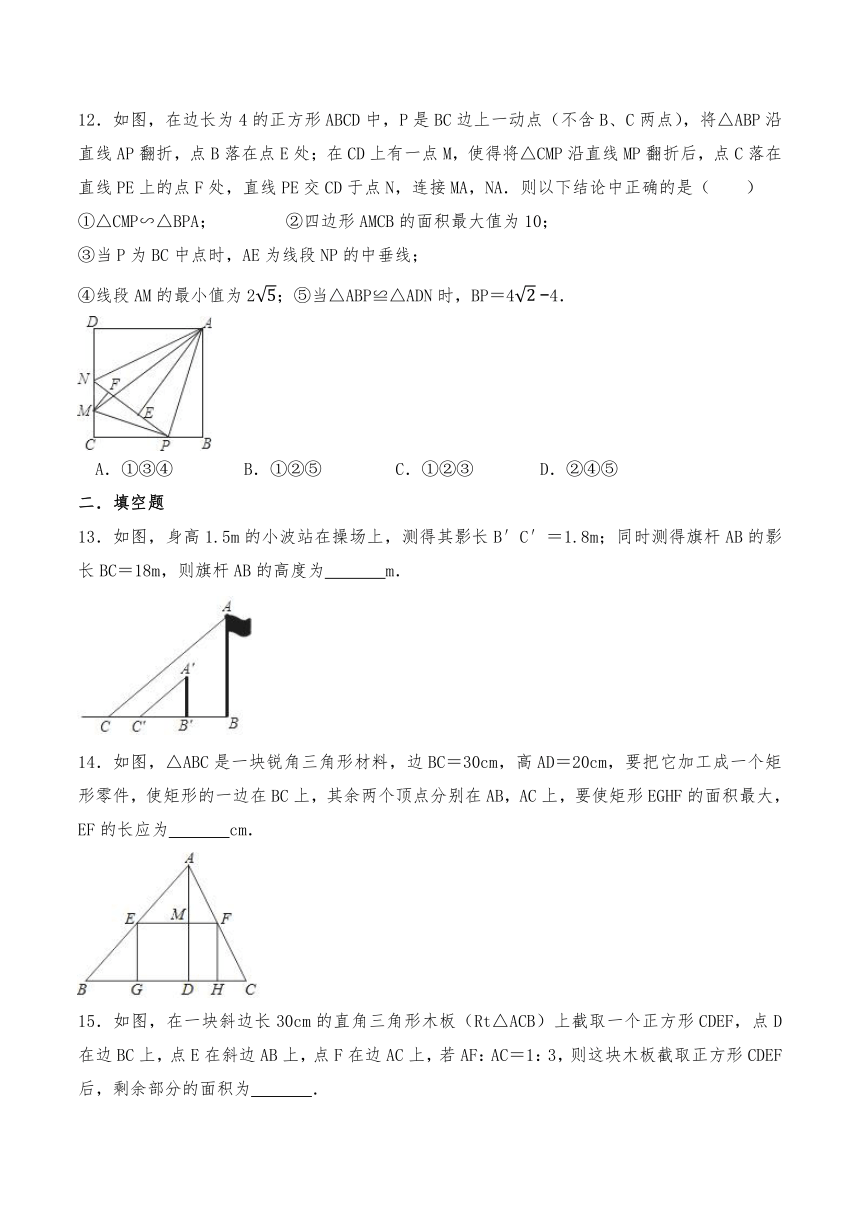
12.如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的是( )
①△CMP∽△BPA; ②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2;⑤当△ABP≌△ADN时,BP=44.
A.①③④ B.①②⑤ C.①②③ D.②④⑤
二.填空题
13.如图,身高1.5m的小波站在操场上,测得其影长B′C′=1.8m;同时测得旗杆AB的影长BC=18m,则旗杆AB的高度为 m.
14.如图,△ABC是一块锐角三角形材料,边BC=30cm,高AD=20cm,要把它加工成一个矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB,AC上,要使矩形EGHF的面积最大,EF的长应为 cm.
15.如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为 .
16.用杠杆撬石头的示意图如图所示,P是支点,当用力压杠杆的A端时,杠杆绕P点转动,另一端B向上翘起,石头就被撬动.现有一块石头要使其滚动,杠杆的B端必须向上翘起8cm,已知杠杆的动力臂AP与阻力臂BP之比为4:1,要使这块石头滚动,至少要将杠杆的A端向下压 cm.
17.如图,两根竖直的电线杆AB长为12,CD长为4,AD交BC于点E,则点E到地面的距离EF的长是 .
18.我国古代数学著作中记载了一个问题:“今有邑方不知大小,各开中门,出北门二十步有木,出西门四十五步见木,问:邑方几何?”其大意是:一座正方形城池,西、北边正中各开一道门,从北门往正北方向走20步后刚好有一树木,若从西门往正西方向走45步后正好看到树木,则正方形城池的边长为 步.
19.利用标杆CD测量建筑物的高度的示意图如图所示,使标杆顶端的影子与建筑物顶端的影子恰好落在地面的同一点E.若标杆CD的高为1.5米,测得DE=2米,BD=16米,则建筑物的高AB为 米.
20.如图,一位同学通过调整自己的位置,设法使三角板DEF的斜边DF保持水平,并且边DE与点B在同一直线上,已知两条边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB为 m.
21.如图,比例规是一种画图工具,使用它可以把线段按一定的比例伸长或缩短,它是由长度相等的两脚AD和BC交叉构成的,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A、B两个尖端分别在线段l的两端上,若CD=2,则AB的长是 .
22.如图,电线杆上的路灯距离地面8m,身高1.6m的小明(AB)站在距离电线杆的底部(点O)20m的A处,则小明的影子AM长为 m.
23.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,以点A为原点建立平面直角坐标系,使AB在x轴正半轴上,点D是AC边上的一个动点,DE∥AB交BC于E,DF⊥AB于F,EG⊥AB于G.以下结论:
①△AFD∽△DCE∽△EGB;
②当D为AC的中点时,△AFD≌△DCE;
③点C的坐标为(3.2,2.4);
④将△ABC沿AC所在的直线翻折到原来的平面,点B的对应点B1的坐标为(1.6,4.8);
⑤矩形DEGF的最大面积为3.在这些结论中正确的有 (只填序号)
24.如图,点P是边长为2的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论:①MF=MC;②AH⊥EF;③AP2=PM PH; ④EF的最小值是.其中正确的是 .(把你认为正确结论的序号都填上)
三.解答题
25.某班在学习《利用相似三角形测高》时开展了“测量学校操场上旗杆的高度”的活动.小明将镜子放在离旗杆32m的点C处(即AC=32m),然后沿直线AC后退,在点D处恰好看到旗杆顶端B在镜子中的像与镜子上的标记重合(如图),根据物理学知识可知:法线l⊥AD,∠1=∠2.若小明的眼睛离地面的高度DE为1.5m,CD=3m,求旗杆AB的高度.(要有证明过程,再求值)
26.如图,一块材料的形状是锐角三角形ABC,边BC长13cm,BC边上的高AD为6cm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上.
(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长.
27.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50cm,DE=40cm,测得边DF离地面的高度AC=1.5m,CD=12m,求树高AB.
28.AD是△ABC的中线,G是AD上任意一点时(点G不与A重合),过点G的直线交边AB于E,交射线AC于点F,设AE=xAB,AF=yAC(x、y≠0).
(1)如图1,若点G与D重合,△ABC为等边三角形,且∠BDE=30°,证明:△AEF∽△DEA;
(2)如图2,若点G与D重合,证明:2;
(3)如图3,若AG=nAD,x,y,直接写出n的值.
29.已知不等臂跷跷板AB长为3米.跷跷板AB的支撑点O到地面的点H的距离OH=0.6米.当跷跷板AB的一个端点A碰到地面时(如图1),AB与直线AH的夹角∠OAH的度数为30°.
(1)当AB的另一个端点B碰到地面时(如图2),跷跷板AB与直线BH的夹角∠ABH的正弦值是多少?
(2)当AB的另一个端点B碰到地面时(如图2),点A到直线BH的距离是多少米?
30.已知在菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,联结PC.在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.
(1)如图,当点P在边AB上时,如果BP=3,求线段PC的长;
(2)当点P在射线BA上时,设BP=x,CQ=y,求y关于x的函数解析式及定义域;
(3)联结PQ,直线PQ与直线BC交于点E,如果△QCE与△BCP相似,求线段BP的长.
答案
一.选择题
A.A.D.C.A.C.B.B.A.B.A.B.
二.填空题
13.15.
14.15.
15.100cm2.
16.32.
17.3.
18.60.
19.13.5
20.5.5.
21.6.
22.5.
23.①③⑤.
24.②③④.
三.解答题
25.解:∵法线l⊥AD,∠1=∠2,
∴∠ECD=∠BCA,
又∵∠EDC=∠BAC=90°,
∴△ECD∽△BCA,
∴,
∵DE=1.5m,CD=3m,AC=32m,
∴,
解得:AB=16,
答:旗杆AB的高度为16m.
26.解:(1)∵正方形EGHF,
∴EF∥BC,
∴△AEF∽△ABC,
(2)设EG=EF=x
∵△AEF∽△ABC
∴,
∴,
∴x,
∴正方形零件的边长为cm.
27.解:在Rt△DEF中,DE2+EF2=DF2,
即:402+EF2=502,
∴EF=30,
由题意得:∠BCD=∠DEF=90°,∠CDB=∠EDF,
∴△DCB∽△DEF,
∴,
∵EF=30cm=0.3m,DE=40cm=0.4m,CD=12m,
∴,
解得:BC=9米,
∵AC=1.5m,
∴AB=AC+BC=1.5+9=10.5m.
28.解:(1)∵△ABC为等边三角形,
∴∠BAC=∠B=60°,AB=AC,
∵AD是△ABC的中线,
∴∠BAD∠BAC=30°,
∵∠BDE=30°,
∴∠EF⊥AB,
∴∠F=30°=∠BAD,
∵∠AED=∠FEA=90°,
∴△AEF∽△DEA;
(2)如图2,过C作CH∥AB交EF于H,
∴∠B=∠DCH,∠BED=∠CHD,
∵AD是△ABC的中线,
∴BD=CD,
∴△DEB≌△DHC(AAS),
∴CH=BE,
∵CH∥AB,
∴△FCH∽△FAE,
∴,
∴,
∵,,
∴11,11
∴11,
∴2;
(3)如图3,∵y,
∴AFAC,
∴ACAF,
∵x,
∴AEAB,
∴点E是AB的中点,
∵AD是△ABC的中线,
∴点D是BC的中点,
∴DEAC AFAF,DE∥AC,
∴△DGE∽△AGF,
∴,
∴DGAG,
∴AD=AG+DG=AGAGAG,
∴AGAD=nAD,
∴n.
29.(1)证明:在Rt△AOH中,
∵∠AHO=90°,∠AOH=30°,OH=0.6,
∴AO=2OH=2×0.6=1.2(m),
∴OB=AB﹣OA=3﹣1.2=1.8(m),
在Rt△BOH中,
∵∠BHO=90°,OH=0.6,OB=1.8,
∴;
(2)解:过点A向直线BH作垂线,垂足为M,
在Rt△ABM中,
∵∠AMB=90°,,AB=3,
∴,
答:∠ABH的正弦值为,点A到直线BH的距离是1米.
30.解:(1)如图1中,作PH⊥BC于H.
∵四边形ABCD是菱形,
∴AB=BC=4,AD∥BC,
∴∠A+∠ABC=180°,
∵∠A=120°,
∴∠PBH=60°,
∵PB=3,∠PHB=90°,
∴BH=PB cos60°,PH=PB sin60°,
∴CH=BC﹣BH=4,
∴PC.
(2)如图1中,作PH⊥BC于H,连接PQ,设PC交BD于O.
∵四边形ABCD是菱形,
∴∠ABD=∠CBD=30°,
∵∠PCQ=30°,
∴∠PBO=∠QCO,
∵∠POB=∠QOC,
∴△POB∽△QOC,
∴,
∴,
∵∠POQ=∠BOC,
∴△POQ∽△BOC,
∴∠OPQ=∠OBC=30°=∠PCQ,
∴PQ=CQ=y,
∴PCy,
在Rt△PHB中,BHx,PHx,
∵PC2=PH2+CH2,
∴3y2=(x)2+(4x)2,
∴y(0≤x<8).
(3)①如图2中,若直线QP交直线BC于B点左侧于E.
此时∠CQE=120°,
∵∠PBC=60°,
∴△PBC中,不存在角与∠CQE相等,
此时△QCE与△BCP不可能相似.
②如图3中,若直线QP交直线BC于C点右侧于E.
则∠CQE=∠B=QBC+∠QCP=60°=∠CBP,
∵∠PCB>∠E,
∴只可能∠BCP=∠QCE=75°,
作CF⊥AB于F,则BF=2,CF=2,∠PCF=45°,
∴PF=CF=2,
此时PB=2+2,
③如图4中,当点P在AB的延长线上时,
∵△QCE与△BCP相似,
∴∠CQE=∠CBP=120°,
∴∠QCE=∠PCB=15°,
作CF⊥AB于F.
∵∠FCB=30°,
∴∠FCP=45°,
∴BFBC=2,CF=PF=2,
∴PB=22.
综上所述,满足条件的PB的值为2+2或22.
一.选择题
1.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5m,测得AB=1.2m,BC=12.8m,则建筑物CD的高是( )
A.17.5m B.17m C.16.5m D.18m
2.数学兴趣小组的同学们来到宝安区海淀广场,设计用手电来测量广场附近某大厦CD的高度,如图,点P处放一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1米,BP=1.5米,PD=48米,那么该大厦的高度约为( )
A.32米 B.28米 C.24米 D.16米
3.如图,某同学拿着一把12cm长的尺子,站在距电线杆30m的位置,把手臂向前伸直,将尺子竖直,看到尺子恰好遮住电线杆,已知臂长60cm,则电线杆的高度是( )
A.2.4m B.24m C.0.6m D.6m
4.如图为一座房屋屋架结构示意图,已知屋檐AB=BC,横梁EF∥AC,点E为AB的中点,且BD⊥EF,屋架高BD=4m,横梁AC=12m,则支架DF长为( )
A.2 B.2 C. D.2
5.如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A.100cm2 B.150cm2 C.170cm2 D.200cm2
6.小亮利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是他剪裁出的空心等边三角形、正方形、矩形、正五边形,若每个图案花边的宽度都相等,那么每个图案中花边的内外边缘所围成的几何图形不相似的是( )
A. B.
C. D.
7.如图,AB和CD表示两根直立于地面的柱子,AC和BD表示起固定作用的两根钢筋,AC与BD相交于点M,已知AB=8m,CD=12m,则点M离地面的高度MH为( )
A.4 m B.m C.5m D.m
8.如图,有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着底边BC修一座底面是矩形DEFG的大楼,则这座大楼的地基面积最大值是( )
A.1000米2 B.2000米2 C.3000米2 D.4000米2
9.如图,有一块三角形余料ABC,BC=120mm,高线AD=80mm,要把它加工成一个矩形零件,使矩形的一边在BC上,点P,M分别在AB,AC上,若满足PM:PQ=3:2,则PM的长为( )
A.60mm B.mm C.20mm D.mm
10.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中第九卷《勾股》章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”
译文:“今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)
你的计算结果是:出南门几何步而见木( )
A.300步 B.315 步 C.400 步 D.415步
11.相邻两根电杆都用钢索在地面上固定,如图,一根电杆钢索系在离地面4米处,另一根电杆钢索系在离地面6米处,则中间两根钢索相交处点P离地面( )
A.2.4米 B.8米
C.3米 D.必须知道两根电线杆的距离才能求出点P离地面距离
12.如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的是( )
①△CMP∽△BPA; ②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2;⑤当△ABP≌△ADN时,BP=44.
A.①③④ B.①②⑤ C.①②③ D.②④⑤
二.填空题
13.如图,身高1.5m的小波站在操场上,测得其影长B′C′=1.8m;同时测得旗杆AB的影长BC=18m,则旗杆AB的高度为 m.
14.如图,△ABC是一块锐角三角形材料,边BC=30cm,高AD=20cm,要把它加工成一个矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB,AC上,要使矩形EGHF的面积最大,EF的长应为 cm.
15.如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为 .
16.用杠杆撬石头的示意图如图所示,P是支点,当用力压杠杆的A端时,杠杆绕P点转动,另一端B向上翘起,石头就被撬动.现有一块石头要使其滚动,杠杆的B端必须向上翘起8cm,已知杠杆的动力臂AP与阻力臂BP之比为4:1,要使这块石头滚动,至少要将杠杆的A端向下压 cm.
17.如图,两根竖直的电线杆AB长为12,CD长为4,AD交BC于点E,则点E到地面的距离EF的长是 .
18.我国古代数学著作中记载了一个问题:“今有邑方不知大小,各开中门,出北门二十步有木,出西门四十五步见木,问:邑方几何?”其大意是:一座正方形城池,西、北边正中各开一道门,从北门往正北方向走20步后刚好有一树木,若从西门往正西方向走45步后正好看到树木,则正方形城池的边长为 步.
19.利用标杆CD测量建筑物的高度的示意图如图所示,使标杆顶端的影子与建筑物顶端的影子恰好落在地面的同一点E.若标杆CD的高为1.5米,测得DE=2米,BD=16米,则建筑物的高AB为 米.
20.如图,一位同学通过调整自己的位置,设法使三角板DEF的斜边DF保持水平,并且边DE与点B在同一直线上,已知两条边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB为 m.
21.如图,比例规是一种画图工具,使用它可以把线段按一定的比例伸长或缩短,它是由长度相等的两脚AD和BC交叉构成的,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A、B两个尖端分别在线段l的两端上,若CD=2,则AB的长是 .
22.如图,电线杆上的路灯距离地面8m,身高1.6m的小明(AB)站在距离电线杆的底部(点O)20m的A处,则小明的影子AM长为 m.
23.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,以点A为原点建立平面直角坐标系,使AB在x轴正半轴上,点D是AC边上的一个动点,DE∥AB交BC于E,DF⊥AB于F,EG⊥AB于G.以下结论:
①△AFD∽△DCE∽△EGB;
②当D为AC的中点时,△AFD≌△DCE;
③点C的坐标为(3.2,2.4);
④将△ABC沿AC所在的直线翻折到原来的平面,点B的对应点B1的坐标为(1.6,4.8);
⑤矩形DEGF的最大面积为3.在这些结论中正确的有 (只填序号)
24.如图,点P是边长为2的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论:①MF=MC;②AH⊥EF;③AP2=PM PH; ④EF的最小值是.其中正确的是 .(把你认为正确结论的序号都填上)
三.解答题
25.某班在学习《利用相似三角形测高》时开展了“测量学校操场上旗杆的高度”的活动.小明将镜子放在离旗杆32m的点C处(即AC=32m),然后沿直线AC后退,在点D处恰好看到旗杆顶端B在镜子中的像与镜子上的标记重合(如图),根据物理学知识可知:法线l⊥AD,∠1=∠2.若小明的眼睛离地面的高度DE为1.5m,CD=3m,求旗杆AB的高度.(要有证明过程,再求值)
26.如图,一块材料的形状是锐角三角形ABC,边BC长13cm,BC边上的高AD为6cm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上.
(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长.
27.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50cm,DE=40cm,测得边DF离地面的高度AC=1.5m,CD=12m,求树高AB.
28.AD是△ABC的中线,G是AD上任意一点时(点G不与A重合),过点G的直线交边AB于E,交射线AC于点F,设AE=xAB,AF=yAC(x、y≠0).
(1)如图1,若点G与D重合,△ABC为等边三角形,且∠BDE=30°,证明:△AEF∽△DEA;
(2)如图2,若点G与D重合,证明:2;
(3)如图3,若AG=nAD,x,y,直接写出n的值.
29.已知不等臂跷跷板AB长为3米.跷跷板AB的支撑点O到地面的点H的距离OH=0.6米.当跷跷板AB的一个端点A碰到地面时(如图1),AB与直线AH的夹角∠OAH的度数为30°.
(1)当AB的另一个端点B碰到地面时(如图2),跷跷板AB与直线BH的夹角∠ABH的正弦值是多少?
(2)当AB的另一个端点B碰到地面时(如图2),点A到直线BH的距离是多少米?
30.已知在菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,联结PC.在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.
(1)如图,当点P在边AB上时,如果BP=3,求线段PC的长;
(2)当点P在射线BA上时,设BP=x,CQ=y,求y关于x的函数解析式及定义域;
(3)联结PQ,直线PQ与直线BC交于点E,如果△QCE与△BCP相似,求线段BP的长.
答案
一.选择题
A.A.D.C.A.C.B.B.A.B.A.B.
二.填空题
13.15.
14.15.
15.100cm2.
16.32.
17.3.
18.60.
19.13.5
20.5.5.
21.6.
22.5.
23.①③⑤.
24.②③④.
三.解答题
25.解:∵法线l⊥AD,∠1=∠2,
∴∠ECD=∠BCA,
又∵∠EDC=∠BAC=90°,
∴△ECD∽△BCA,
∴,
∵DE=1.5m,CD=3m,AC=32m,
∴,
解得:AB=16,
答:旗杆AB的高度为16m.
26.解:(1)∵正方形EGHF,
∴EF∥BC,
∴△AEF∽△ABC,
(2)设EG=EF=x
∵△AEF∽△ABC
∴,
∴,
∴x,
∴正方形零件的边长为cm.
27.解:在Rt△DEF中,DE2+EF2=DF2,
即:402+EF2=502,
∴EF=30,
由题意得:∠BCD=∠DEF=90°,∠CDB=∠EDF,
∴△DCB∽△DEF,
∴,
∵EF=30cm=0.3m,DE=40cm=0.4m,CD=12m,
∴,
解得:BC=9米,
∵AC=1.5m,
∴AB=AC+BC=1.5+9=10.5m.
28.解:(1)∵△ABC为等边三角形,
∴∠BAC=∠B=60°,AB=AC,
∵AD是△ABC的中线,
∴∠BAD∠BAC=30°,
∵∠BDE=30°,
∴∠EF⊥AB,
∴∠F=30°=∠BAD,
∵∠AED=∠FEA=90°,
∴△AEF∽△DEA;
(2)如图2,过C作CH∥AB交EF于H,
∴∠B=∠DCH,∠BED=∠CHD,
∵AD是△ABC的中线,
∴BD=CD,
∴△DEB≌△DHC(AAS),
∴CH=BE,
∵CH∥AB,
∴△FCH∽△FAE,
∴,
∴,
∵,,
∴11,11
∴11,
∴2;
(3)如图3,∵y,
∴AFAC,
∴ACAF,
∵x,
∴AEAB,
∴点E是AB的中点,
∵AD是△ABC的中线,
∴点D是BC的中点,
∴DEAC AFAF,DE∥AC,
∴△DGE∽△AGF,
∴,
∴DGAG,
∴AD=AG+DG=AGAGAG,
∴AGAD=nAD,
∴n.
29.(1)证明:在Rt△AOH中,
∵∠AHO=90°,∠AOH=30°,OH=0.6,
∴AO=2OH=2×0.6=1.2(m),
∴OB=AB﹣OA=3﹣1.2=1.8(m),
在Rt△BOH中,
∵∠BHO=90°,OH=0.6,OB=1.8,
∴;
(2)解:过点A向直线BH作垂线,垂足为M,
在Rt△ABM中,
∵∠AMB=90°,,AB=3,
∴,
答:∠ABH的正弦值为,点A到直线BH的距离是1米.
30.解:(1)如图1中,作PH⊥BC于H.
∵四边形ABCD是菱形,
∴AB=BC=4,AD∥BC,
∴∠A+∠ABC=180°,
∵∠A=120°,
∴∠PBH=60°,
∵PB=3,∠PHB=90°,
∴BH=PB cos60°,PH=PB sin60°,
∴CH=BC﹣BH=4,
∴PC.
(2)如图1中,作PH⊥BC于H,连接PQ,设PC交BD于O.
∵四边形ABCD是菱形,
∴∠ABD=∠CBD=30°,
∵∠PCQ=30°,
∴∠PBO=∠QCO,
∵∠POB=∠QOC,
∴△POB∽△QOC,
∴,
∴,
∵∠POQ=∠BOC,
∴△POQ∽△BOC,
∴∠OPQ=∠OBC=30°=∠PCQ,
∴PQ=CQ=y,
∴PCy,
在Rt△PHB中,BHx,PHx,
∵PC2=PH2+CH2,
∴3y2=(x)2+(4x)2,
∴y(0≤x<8).
(3)①如图2中,若直线QP交直线BC于B点左侧于E.
此时∠CQE=120°,
∵∠PBC=60°,
∴△PBC中,不存在角与∠CQE相等,
此时△QCE与△BCP不可能相似.
②如图3中,若直线QP交直线BC于C点右侧于E.
则∠CQE=∠B=QBC+∠QCP=60°=∠CBP,
∵∠PCB>∠E,
∴只可能∠BCP=∠QCE=75°,
作CF⊥AB于F,则BF=2,CF=2,∠PCF=45°,
∴PF=CF=2,
此时PB=2+2,
③如图4中,当点P在AB的延长线上时,
∵△QCE与△BCP相似,
∴∠CQE=∠CBP=120°,
∴∠QCE=∠PCB=15°,
作CF⊥AB于F.
∵∠FCB=30°,
∴∠FCP=45°,
∴BFBC=2,CF=PF=2,
∴PB=22.
综上所述,满足条件的PB的值为2+2或22.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
