九年级数学下册试题 7.5解直角三角形 苏科版(含答案)
文档属性
| 名称 | 九年级数学下册试题 7.5解直角三角形 苏科版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 148.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 18:07:12 | ||
图片预览


文档简介
7.5解直角三角形
一.选择题
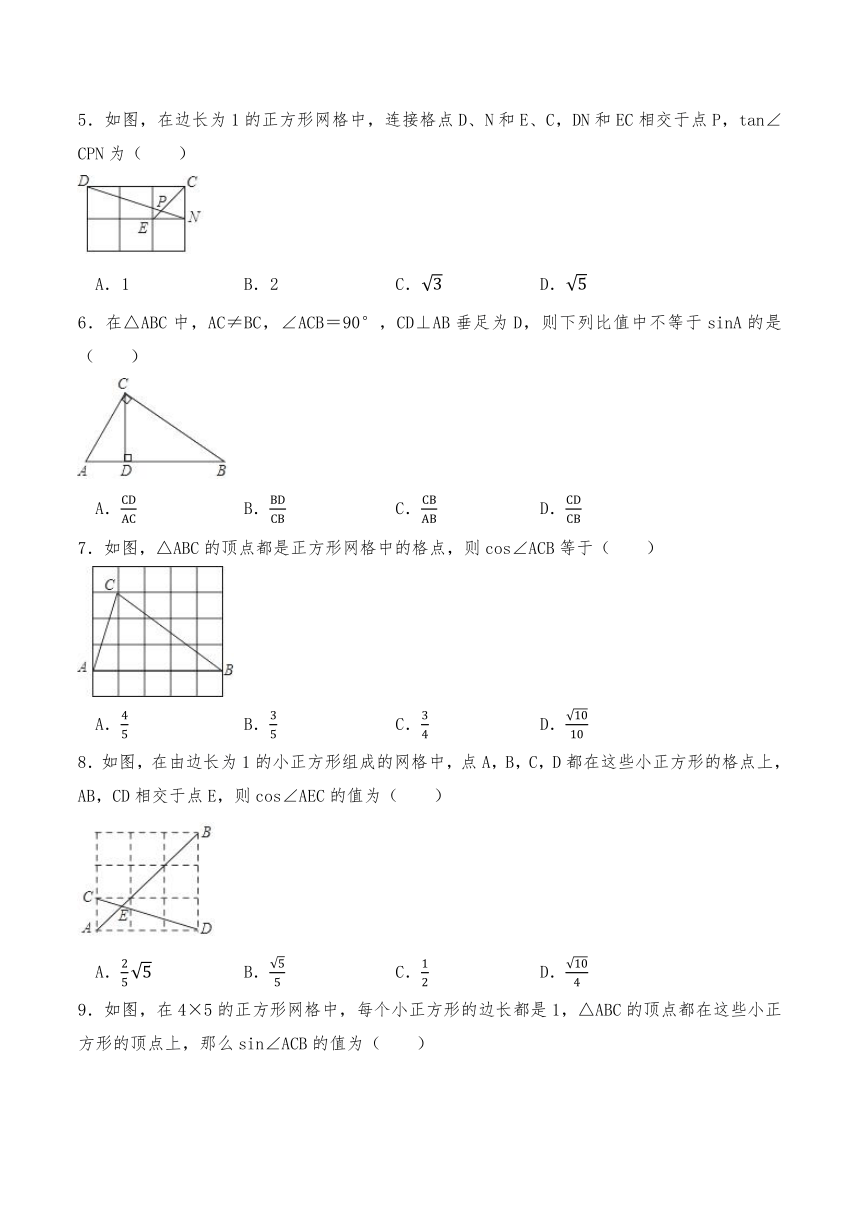
1.如图,已知在平面直角坐标系xOy内有一点A(2,3),那么OA与x轴正半轴的夹角α的余切值是( )
A. B. C. D.
2.在平面直角坐标系xOy中,点A的坐标为(1,2),如果射线OA与x轴正半轴的夹角为α,那么sinα的值是( )
A. B. C. D.2
3.如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为( )
A. B. C.2 D.2
4.如图,已知A、B两点的坐标分别为(8,0)、(0,8),点C、F分别是直线x=﹣5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE面积取得最小值时,tan∠BAD的值是( )
A. B. C. D.
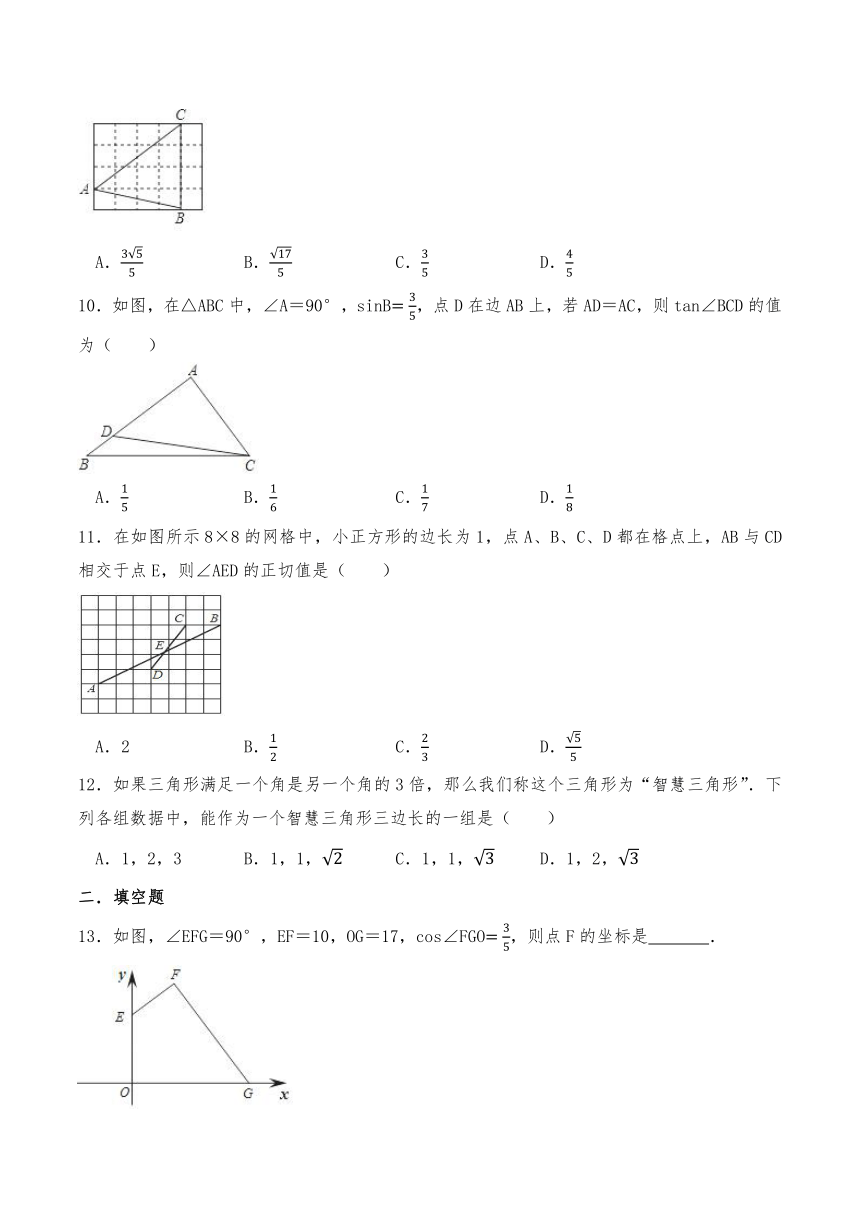
5.如图,在边长为1的正方形网格中,连接格点D、N和E、C,DN和EC相交于点P,tan∠CPN为( )
A.1 B.2 C. D.
6.在△ABC中,AC≠BC,∠ACB=90°,CD⊥AB垂足为D,则下列比值中不等于sinA的是( )
A. B. C. D.
7.如图,△ABC的顶点都是正方形网格中的格点,则cos∠ACB等于( )
A. B. C. D.
8.如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在这些小正方形的格点上,AB,CD相交于点E,则cos∠AEC的值为( )
A. B. C. D.
9.如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为( )
A. B. C. D.
10.如图,在△ABC中,∠A=90°,sinB,点D在边AB上,若AD=AC,则tan∠BCD的值为( )
A. B. C. D.
11.在如图所示8×8的网格中,小正方形的边长为1,点A、B、C、D都在格点上,AB与CD相交于点E,则∠AED的正切值是( )
A.2 B. C. D.
12.如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )
A.1,2,3 B.1,1, C.1,1, D.1,2,
二.填空题
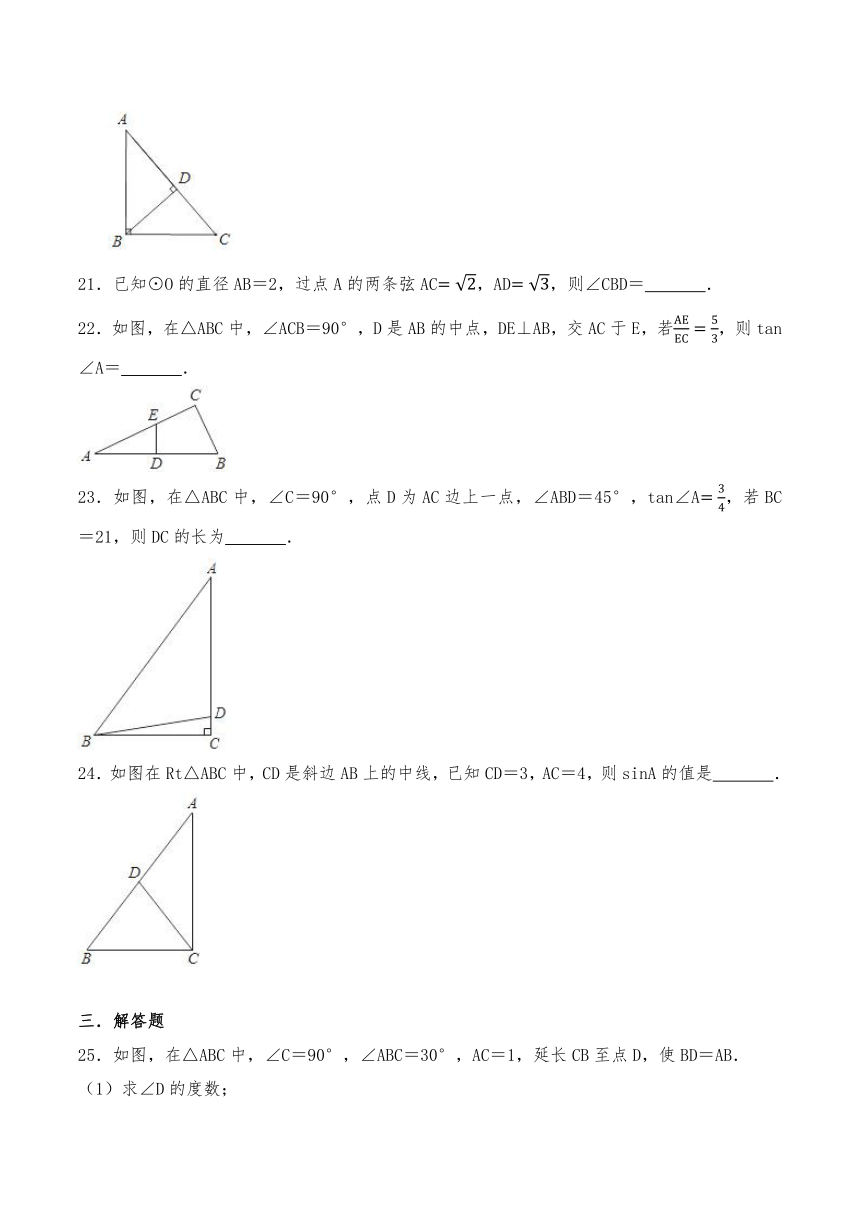
13.如图,∠EFG=90°,EF=10,OG=17,cos∠FGO,则点F的坐标是 .
14.如图,在△ABC中,∠A=30°,∠B=45°,AC=6,则AB的长为 .
15.已知等腰三角形中,腰长是10cm,底边长是16cm,则底角的正切值为 .
16.如图,△ABC为等腰直角三角形,∠ABC=90°,过点B作BQ∥AC,在BQ上取一点D,连接CD、AD,若AC=CD,BD,则AD= .
17.等腰三角形的腰长为1cm,底边长为cm,则它的底角的正切值为 .
18.如图,在△ABC中,∠C=90°,AC=5cm,∠BAC的平分线交BC于D,ADcm,则∠B= ,AB= ,BC= .
19.如图,在△ABC中,tan∠B=2,∠ACB=45°,AD⊥BC于点D,CE⊥AB于点E,AD、CE交于点F,若AC=5,则线段EF的长为 .
20.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC,垂足为点D,如果BC=4,sin∠DBC,那么线段AB的长是 .
21.已知⊙O的直径AB=2,过点A的两条弦AC,AD,则∠CBD= .
22.如图,在△ABC中,∠ACB=90°,D是AB的中点,DE⊥AB,交AC于E,若,则tan∠A= .
23.如图,在△ABC中,∠C=90°,点D为AC边上一点,∠ABD=45°,tan∠A,若BC=21,则DC的长为 .
24.如图在Rt△ABC中,CD是斜边AB上的中线,已知CD=3,AC=4,则sinA的值是 .
三.解答题
25.如图,在△ABC中,∠C=90°,∠ABC=30°,AC=1,延长CB至点D,使BD=AB.
(1)求∠D的度数;
(2)求tan75°的值.(结果可以保留根号)
26.如图,△ABC中,∠B=45°,AB=3,D是BC中点,tanC,求BC的长与tan∠ADB.
27.如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB于点E,连接CE.
(1)求BE的长;
(2)求tan∠ECB的值.
28.如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=CD,∠ADC=90°,连接BD,若△BCD的面积为10,则AD的长为多少?
29.已知:如图,AB是⊙O的直径,PB切⊙O于点B,PA交⊙O于点C,∠A=60°,∠APB的平分线PF分别交BC、AB于点D、E,交⊙O于点F、G,且BD AE=2.
(1)求证:△BPD∽△APE;
(2)求FE EG的值;
(3)求tan∠BDE的值.
30.求证:若α为锐角,则sin2α+cos2α=1.
要求:①如图,锐角α和线段m用尺规作出一个以线段m为直角边,α为内角的Rt△ABC保留作图痕迹,不写作法)
②根据①中所画图形证明该命题.
答案
一.选择题
B.A.A.B.B.D.D.B.D.C.B.D.
二.填空题
13.(8,12).
14.3+3.
15..
16.2.
17..
18.30°,10cm,5cm.
19..
20.2.
21.15°或105°.
22..
23.3.
24..
三.解答题
25.解:(1)∵BD=AB,
∴∠D=∠BAC,
∵∠ABC=30°,
∴∠D=∠DAB=15°,
(2)∵∠C=90°,∠ABC=30°,AC=1,
∴AB=BD=2,BC,
∴CD=2,
∵∠D=15°,
∴∠DAC=75°,
∴tan75°=tan∠CAD2.
26.解:作AE⊥BC于点E,
∵∠B=45°,AB=3,∠AEB=90°,
∴∠B=∠45°,
∴AE=BE=3,
∵tanC,
∴CE=5AE=15,
∴BC=BE+CE=3+15=18,
∵BC=18,点D为BC的中点,
∴BD=9,
∴DE=BD﹣BE=6,
∴tan∠ADB,
即BC=18,tan∠ADB.
27.解:(1)由勾股定理得,AB3,
由题意得,AD=2,CD=1,
∵∠AED=∠ACB=90°,∠A=∠A,
∴△AED∽△ACB,
∴,即,
解得,AE,
∴BE=AB﹣AE=2;
(2)作EF⊥BC于F,
则EF∥AC,
∴△BEF∽△BAC,
∴,即,
解得,EF=2,BF=2,
∴CF=1,
∴tan∠ECB2.
28.解:过D作DH⊥BC于H,过A作AM⊥BC于M,过D作DG⊥AM于G.
设CM=a,
∵AB=AC,
∴BC=2CM=2a,
∵tan∠ACB=2,
∴2,
∴AM=2a,
由勾股定理得:ACa,
∵S△BDCBC DH=10,
∴2a×DH=10,
∴DH
∵∠DHM=∠HMG=∠MGD=90°,
∴四边形DHMG为矩形,
∴∠HDG=90°=∠HDC+∠CDG,DG=HM,DH=MG,
∵∠ADC=90°=∠ADG+∠CDG,
∴∠ADG=∠CDH,
在△ADG和△CDH中,
∵,
∴△ADG≌△CDH(AAS),
∴DG=DH=MG,AG=CH=a
∴AM=AG+MG,
即2a=a,
a2=20,
在Rt△ADC中,AD2+CD2=AC2,
∵AD=CD,
∴2AD2=5a2=100,
∴AD=5或﹣5(舍),
故答案为:5.
29.(1)证明:∵BP切⊙O于点B,
∴∠PBC=∠A.
又∵PF为∠APB的角平分线,
∴∠APE=∠BPD.
∴△BPD∽△APE.
(2)解:∵△BPD∽△APE,
∴∠BDP=∠AEP.
∴∠BED=∠BDE.
∴BE=BD.
又∵BD AE=2,
∴BE AE=2.
∴FE EG=BE AE=2.
(3)解:∵△BPD∽△APE,
∴.
又∵AB是⊙O的直径,PB切⊙O于点B,
∴∠ABP=90°.
而∠A=60°,
∴sin∠A=sin60°,
∴.
又BD=BE,
∴.
又∵BE AE=2,
∴AE=2,BE.
∴AB=2,tan60°.
∴PB=23.
∴tan∠BDE=tan∠BED.
30.解:①如图,Rt△ABC即为所求.
②∵sinα,cosα,AB2=BC2+AC2,
∴sin2α+cos2α1.
一.选择题
1.如图,已知在平面直角坐标系xOy内有一点A(2,3),那么OA与x轴正半轴的夹角α的余切值是( )
A. B. C. D.
2.在平面直角坐标系xOy中,点A的坐标为(1,2),如果射线OA与x轴正半轴的夹角为α,那么sinα的值是( )
A. B. C. D.2
3.如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为( )
A. B. C.2 D.2
4.如图,已知A、B两点的坐标分别为(8,0)、(0,8),点C、F分别是直线x=﹣5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE面积取得最小值时,tan∠BAD的值是( )
A. B. C. D.
5.如图,在边长为1的正方形网格中,连接格点D、N和E、C,DN和EC相交于点P,tan∠CPN为( )
A.1 B.2 C. D.
6.在△ABC中,AC≠BC,∠ACB=90°,CD⊥AB垂足为D,则下列比值中不等于sinA的是( )
A. B. C. D.
7.如图,△ABC的顶点都是正方形网格中的格点,则cos∠ACB等于( )
A. B. C. D.
8.如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在这些小正方形的格点上,AB,CD相交于点E,则cos∠AEC的值为( )
A. B. C. D.
9.如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为( )
A. B. C. D.
10.如图,在△ABC中,∠A=90°,sinB,点D在边AB上,若AD=AC,则tan∠BCD的值为( )
A. B. C. D.
11.在如图所示8×8的网格中,小正方形的边长为1,点A、B、C、D都在格点上,AB与CD相交于点E,则∠AED的正切值是( )
A.2 B. C. D.
12.如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )
A.1,2,3 B.1,1, C.1,1, D.1,2,
二.填空题
13.如图,∠EFG=90°,EF=10,OG=17,cos∠FGO,则点F的坐标是 .
14.如图,在△ABC中,∠A=30°,∠B=45°,AC=6,则AB的长为 .
15.已知等腰三角形中,腰长是10cm,底边长是16cm,则底角的正切值为 .
16.如图,△ABC为等腰直角三角形,∠ABC=90°,过点B作BQ∥AC,在BQ上取一点D,连接CD、AD,若AC=CD,BD,则AD= .
17.等腰三角形的腰长为1cm,底边长为cm,则它的底角的正切值为 .
18.如图,在△ABC中,∠C=90°,AC=5cm,∠BAC的平分线交BC于D,ADcm,则∠B= ,AB= ,BC= .
19.如图,在△ABC中,tan∠B=2,∠ACB=45°,AD⊥BC于点D,CE⊥AB于点E,AD、CE交于点F,若AC=5,则线段EF的长为 .
20.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC,垂足为点D,如果BC=4,sin∠DBC,那么线段AB的长是 .
21.已知⊙O的直径AB=2,过点A的两条弦AC,AD,则∠CBD= .
22.如图,在△ABC中,∠ACB=90°,D是AB的中点,DE⊥AB,交AC于E,若,则tan∠A= .
23.如图,在△ABC中,∠C=90°,点D为AC边上一点,∠ABD=45°,tan∠A,若BC=21,则DC的长为 .
24.如图在Rt△ABC中,CD是斜边AB上的中线,已知CD=3,AC=4,则sinA的值是 .
三.解答题
25.如图,在△ABC中,∠C=90°,∠ABC=30°,AC=1,延长CB至点D,使BD=AB.
(1)求∠D的度数;
(2)求tan75°的值.(结果可以保留根号)
26.如图,△ABC中,∠B=45°,AB=3,D是BC中点,tanC,求BC的长与tan∠ADB.
27.如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB于点E,连接CE.
(1)求BE的长;
(2)求tan∠ECB的值.
28.如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=CD,∠ADC=90°,连接BD,若△BCD的面积为10,则AD的长为多少?
29.已知:如图,AB是⊙O的直径,PB切⊙O于点B,PA交⊙O于点C,∠A=60°,∠APB的平分线PF分别交BC、AB于点D、E,交⊙O于点F、G,且BD AE=2.
(1)求证:△BPD∽△APE;
(2)求FE EG的值;
(3)求tan∠BDE的值.
30.求证:若α为锐角,则sin2α+cos2α=1.
要求:①如图,锐角α和线段m用尺规作出一个以线段m为直角边,α为内角的Rt△ABC保留作图痕迹,不写作法)
②根据①中所画图形证明该命题.
答案
一.选择题
B.A.A.B.B.D.D.B.D.C.B.D.
二.填空题
13.(8,12).
14.3+3.
15..
16.2.
17..
18.30°,10cm,5cm.
19..
20.2.
21.15°或105°.
22..
23.3.
24..
三.解答题
25.解:(1)∵BD=AB,
∴∠D=∠BAC,
∵∠ABC=30°,
∴∠D=∠DAB=15°,
(2)∵∠C=90°,∠ABC=30°,AC=1,
∴AB=BD=2,BC,
∴CD=2,
∵∠D=15°,
∴∠DAC=75°,
∴tan75°=tan∠CAD2.
26.解:作AE⊥BC于点E,
∵∠B=45°,AB=3,∠AEB=90°,
∴∠B=∠45°,
∴AE=BE=3,
∵tanC,
∴CE=5AE=15,
∴BC=BE+CE=3+15=18,
∵BC=18,点D为BC的中点,
∴BD=9,
∴DE=BD﹣BE=6,
∴tan∠ADB,
即BC=18,tan∠ADB.
27.解:(1)由勾股定理得,AB3,
由题意得,AD=2,CD=1,
∵∠AED=∠ACB=90°,∠A=∠A,
∴△AED∽△ACB,
∴,即,
解得,AE,
∴BE=AB﹣AE=2;
(2)作EF⊥BC于F,
则EF∥AC,
∴△BEF∽△BAC,
∴,即,
解得,EF=2,BF=2,
∴CF=1,
∴tan∠ECB2.
28.解:过D作DH⊥BC于H,过A作AM⊥BC于M,过D作DG⊥AM于G.
设CM=a,
∵AB=AC,
∴BC=2CM=2a,
∵tan∠ACB=2,
∴2,
∴AM=2a,
由勾股定理得:ACa,
∵S△BDCBC DH=10,
∴2a×DH=10,
∴DH
∵∠DHM=∠HMG=∠MGD=90°,
∴四边形DHMG为矩形,
∴∠HDG=90°=∠HDC+∠CDG,DG=HM,DH=MG,
∵∠ADC=90°=∠ADG+∠CDG,
∴∠ADG=∠CDH,
在△ADG和△CDH中,
∵,
∴△ADG≌△CDH(AAS),
∴DG=DH=MG,AG=CH=a
∴AM=AG+MG,
即2a=a,
a2=20,
在Rt△ADC中,AD2+CD2=AC2,
∵AD=CD,
∴2AD2=5a2=100,
∴AD=5或﹣5(舍),
故答案为:5.
29.(1)证明:∵BP切⊙O于点B,
∴∠PBC=∠A.
又∵PF为∠APB的角平分线,
∴∠APE=∠BPD.
∴△BPD∽△APE.
(2)解:∵△BPD∽△APE,
∴∠BDP=∠AEP.
∴∠BED=∠BDE.
∴BE=BD.
又∵BD AE=2,
∴BE AE=2.
∴FE EG=BE AE=2.
(3)解:∵△BPD∽△APE,
∴.
又∵AB是⊙O的直径,PB切⊙O于点B,
∴∠ABP=90°.
而∠A=60°,
∴sin∠A=sin60°,
∴.
又BD=BE,
∴.
又∵BE AE=2,
∴AE=2,BE.
∴AB=2,tan60°.
∴PB=23.
∴tan∠BDE=tan∠BED.
30.解:①如图,Rt△ABC即为所求.
②∵sinα,cosα,AB2=BC2+AC2,
∴sin2α+cos2α1.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
