广东省深圳市蛇口育才教育集团育才中学2023-2024学年高一上学期12月阶段检测(二)数学试卷(含答案)
文档属性
| 名称 | 广东省深圳市蛇口育才教育集团育才中学2023-2024学年高一上学期12月阶段检测(二)数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 289.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 23:38:06 | ||
图片预览


文档简介
蛇口育才教育集团育才中学2023-2024学年高一上学期12月阶段检测(二)
数学试题(2023.12)
本试卷共4页,22小题,满分150分.考试用时120分钟.
注意事项:
1.答题前,考生务必将姓名、考生号等填写在答题卡指定位置.将条形码横贴在答题卡“条形码粘贴处”.
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡对应题目选项的答案信息点涂黑.如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
4.考生必须保持答题卡的整洁,考试结束后,请将答题卡交回.
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.
1. 已知集合,,则等于( )
A B. C. D.
2. “”是“”的( )
A. 充分不必要条件
B. 充要条件
C. 必要不充分条件
D. 既不充分也不必要条件
3. 函数的定义域为( )
A. B.
C. D.
4. 若,,( )
A. B. C. D.
5. 设为奇函数,且当时,,则当时,( )
A. B. C. D.
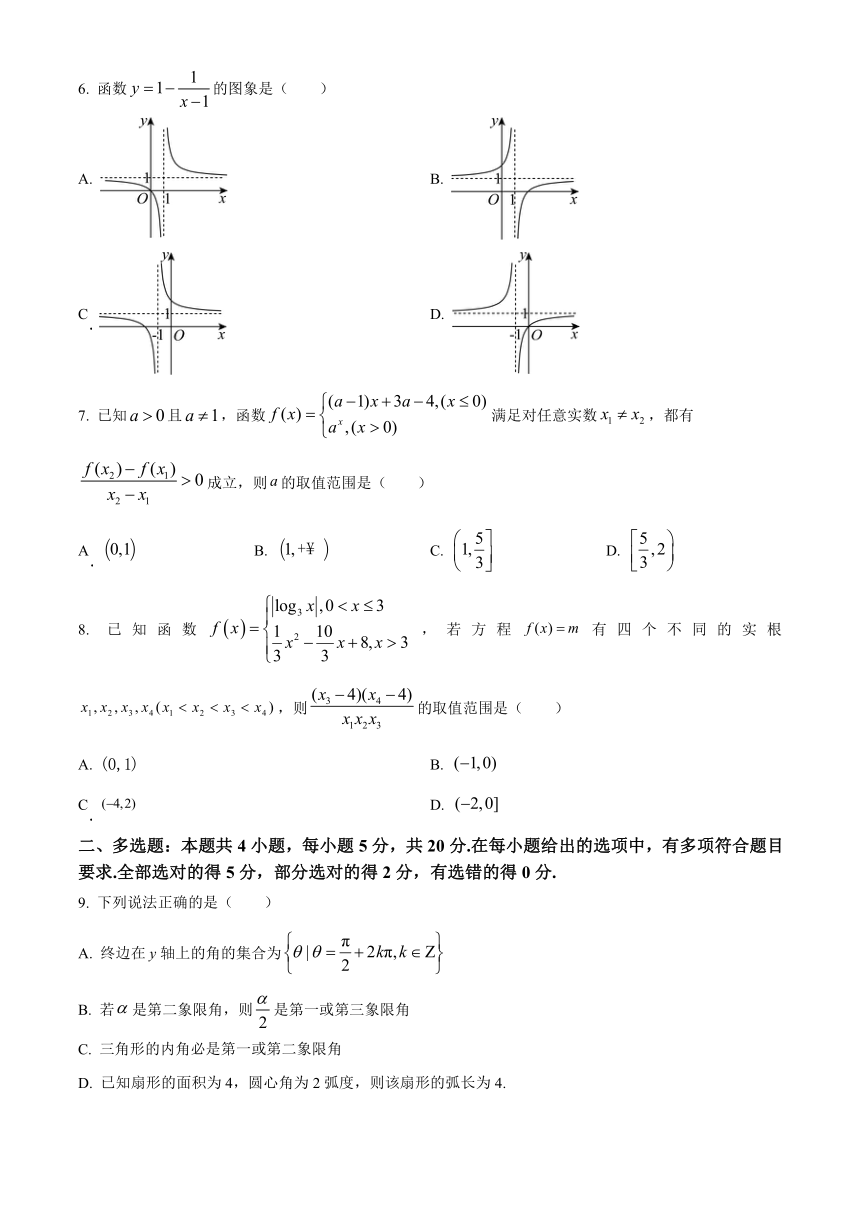
6. 函数的图象是( )
A. B.
C D.
7. 已知且,函数满足对任意实数,都有成立,则的取值范围是( )
A B. C. D.
8. 已知函数,若方程有四个不同的实根,则的取值范围是( )
A. B.
C D.
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 下列说法正确的是( )
A. 终边在y轴上的角的集合为
B. 若是第二象限角,则是第一或第三象限角
C. 三角形的内角必是第一或第二象限角
D. 已知扇形的面积为4,圆心角为2弧度,则该扇形的弧长为4.
10. 已知幂函数的图像经过点,则下列命题正确的有( )
A. 函数为增函数
B. 函数为减函数
C. 若,则
D 若,则
11. 若正实数、满足,则下列说法正确的是( )
A. 有最大值 B. 有最大值
C. 有最小值 D. 有最大值
12. 已知是定义在上的不恒为零的函数,对于任意都满足,则下列说法正确的是( )
A.
B. 是奇函数
C. 若,则
D. 若当时,,则在单调递减
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知,则函数__________.
14. 命题:,.若为真命题,则实数的取值范围是_______.
15. 燕子每年秋天都要从北方飞到南方过冬,研究发现,燕子的飞行速度(单位:)可以表示为(其中是实数,表示燕子的耗氧量的单位数),据统计,燕子在静止的时候其耗氧量为个单位.若燕子为赶路程,飞行的速度不能低于,其耗氧量至少需___________个单位
16. 已知函数,若对任意,存在使得恒成立,则实数a的取值范围为____________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 已知集合.
(1)当时,求;
(2)若,求实数的取值范围.
18. 设函数.
(1)若不等式的解集为,求a,b的值;
(2)若,,,求的最小值和相应的a,b的值.
19. 已知函数(且).
(1)判断函的奇偶性,并说明理由;
(2)若,且,求的取值范围.
20. 已知函数.
(1)若,求在上的值域;
(2)若关于的方程有解,求的取值范围.
21. 长江存储是我国唯一一家能够独立生产3D NAND闪存的公司,其先进的晶栈Xtacking技术使得3D NAND闪存具有极佳的性能和极长的寿命.为了应对第四季度3D NAND闪存颗粒库存积压的情况,某下游闪存封装公司拟对产能进行调整,已知封装闪存的固定成本为300万元,每封装万片,还需要万元的变动成本,通过调研得知,当不超过120万片时,;当超过120万片时,,封装好后的闪存颗粒售价为150元/片,且能全部售完.
(1)求公司获得的利润的函数解析式;
(2)封装多少万片时,公司可获得最大利润?
22. 已知函数为偶函数.
(1)求实数的值;
(2)解关于的不等式;
(3)设,若函数与图象有个公共点,求实数的取值范围.
蛇口育才教育集团育才中学2023-2024学年高一上学期12月阶段检测(二)
数学试题(2023.12) 简要答案
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.
【1题答案】
【答案】C
【2题答案】
【答案】C
【3题答案】
【答案】A
【4题答案】
【答案】D
【5题答案】
【答案】D
【6题答案】
【答案】B
【7题答案】
【答案】C
【8题答案】
【答案】B
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
【9题答案】
【答案】BD
【10题答案】
【答案】AC
【11题答案】
【答案】ABC
【12题答案】
【答案】ABD
三、填空题:本题共4小题,每小题5分,共20分.
【13题答案】
【答案】0
【14题答案】
【答案】
【15题答案】
【答案】80
【16题答案】
【答案】
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
【17题答案】
【答案】(1)
(2)
【18题答案】
【答案】(1)
(2)当且仅当时,的最小值为.
【19题答案】
【答案】(1)偶函数,理由略
(2)
【20题答案】
【答案】(1)
(2)
【21题答案】
【答案】(1)
(2)封装160万片时,公司可获得最大利润
【22题答案】
【答案】(1)
(2)
(3)
数学试题(2023.12)
本试卷共4页,22小题,满分150分.考试用时120分钟.
注意事项:
1.答题前,考生务必将姓名、考生号等填写在答题卡指定位置.将条形码横贴在答题卡“条形码粘贴处”.
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡对应题目选项的答案信息点涂黑.如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
4.考生必须保持答题卡的整洁,考试结束后,请将答题卡交回.
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.
1. 已知集合,,则等于( )
A B. C. D.
2. “”是“”的( )
A. 充分不必要条件
B. 充要条件
C. 必要不充分条件
D. 既不充分也不必要条件
3. 函数的定义域为( )
A. B.
C. D.
4. 若,,( )
A. B. C. D.
5. 设为奇函数,且当时,,则当时,( )
A. B. C. D.
6. 函数的图象是( )
A. B.
C D.
7. 已知且,函数满足对任意实数,都有成立,则的取值范围是( )
A B. C. D.
8. 已知函数,若方程有四个不同的实根,则的取值范围是( )
A. B.
C D.
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 下列说法正确的是( )
A. 终边在y轴上的角的集合为
B. 若是第二象限角,则是第一或第三象限角
C. 三角形的内角必是第一或第二象限角
D. 已知扇形的面积为4,圆心角为2弧度,则该扇形的弧长为4.
10. 已知幂函数的图像经过点,则下列命题正确的有( )
A. 函数为增函数
B. 函数为减函数
C. 若,则
D 若,则
11. 若正实数、满足,则下列说法正确的是( )
A. 有最大值 B. 有最大值
C. 有最小值 D. 有最大值
12. 已知是定义在上的不恒为零的函数,对于任意都满足,则下列说法正确的是( )
A.
B. 是奇函数
C. 若,则
D. 若当时,,则在单调递减
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知,则函数__________.
14. 命题:,.若为真命题,则实数的取值范围是_______.
15. 燕子每年秋天都要从北方飞到南方过冬,研究发现,燕子的飞行速度(单位:)可以表示为(其中是实数,表示燕子的耗氧量的单位数),据统计,燕子在静止的时候其耗氧量为个单位.若燕子为赶路程,飞行的速度不能低于,其耗氧量至少需___________个单位
16. 已知函数,若对任意,存在使得恒成立,则实数a的取值范围为____________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 已知集合.
(1)当时,求;
(2)若,求实数的取值范围.
18. 设函数.
(1)若不等式的解集为,求a,b的值;
(2)若,,,求的最小值和相应的a,b的值.
19. 已知函数(且).
(1)判断函的奇偶性,并说明理由;
(2)若,且,求的取值范围.
20. 已知函数.
(1)若,求在上的值域;
(2)若关于的方程有解,求的取值范围.
21. 长江存储是我国唯一一家能够独立生产3D NAND闪存的公司,其先进的晶栈Xtacking技术使得3D NAND闪存具有极佳的性能和极长的寿命.为了应对第四季度3D NAND闪存颗粒库存积压的情况,某下游闪存封装公司拟对产能进行调整,已知封装闪存的固定成本为300万元,每封装万片,还需要万元的变动成本,通过调研得知,当不超过120万片时,;当超过120万片时,,封装好后的闪存颗粒售价为150元/片,且能全部售完.
(1)求公司获得的利润的函数解析式;
(2)封装多少万片时,公司可获得最大利润?
22. 已知函数为偶函数.
(1)求实数的值;
(2)解关于的不等式;
(3)设,若函数与图象有个公共点,求实数的取值范围.
蛇口育才教育集团育才中学2023-2024学年高一上学期12月阶段检测(二)
数学试题(2023.12) 简要答案
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.
【1题答案】
【答案】C
【2题答案】
【答案】C
【3题答案】
【答案】A
【4题答案】
【答案】D
【5题答案】
【答案】D
【6题答案】
【答案】B
【7题答案】
【答案】C
【8题答案】
【答案】B
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
【9题答案】
【答案】BD
【10题答案】
【答案】AC
【11题答案】
【答案】ABC
【12题答案】
【答案】ABD
三、填空题:本题共4小题,每小题5分,共20分.
【13题答案】
【答案】0
【14题答案】
【答案】
【15题答案】
【答案】80
【16题答案】
【答案】
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
【17题答案】
【答案】(1)
(2)
【18题答案】
【答案】(1)
(2)当且仅当时,的最小值为.
【19题答案】
【答案】(1)偶函数,理由略
(2)
【20题答案】
【答案】(1)
(2)
【21题答案】
【答案】(1)
(2)封装160万片时,公司可获得最大利润
【22题答案】
【答案】(1)
(2)
(3)
同课章节目录
