(10)解直角三角形—2023年初中数学挑战满分全优卷(含解析)
文档属性
| 名称 | (10)解直角三角形—2023年初中数学挑战满分全优卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 00:00:00 | ||
图片预览


文档简介
(10)解直角三角形—2023年初中数学挑战满分全优卷
1.小明喜欢构建几何图形,利用数形结合的思想解决代数问题在计算时,如图,在中,,,延长CB使,连接AD,得,所以,类比小明的方法,计算的值为( )
A. B. C. D.
2.如图,AB是圆的直径,CD是的平分线交圆O于点D,过D作圆O的切线交CB的延长线于点E.若,,则CD的长为( )
A. B.2 C. D.
3.如图,已知扇形OAB的半径为r,C是弧AB上的任一点(不与A,B重合),,垂足为M,,垂足为N,连接MN,若,则MN可用表示为( )
A. B. C. D.
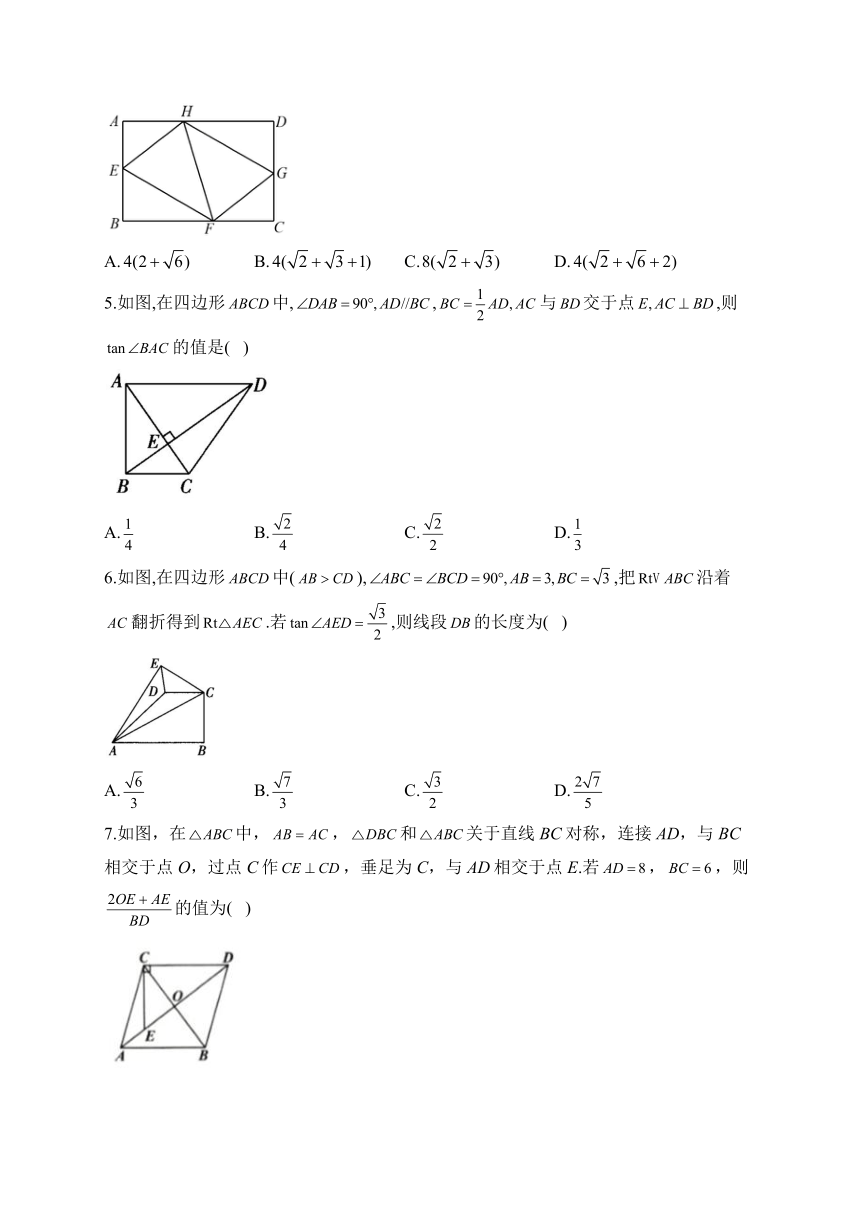
4.如图,E、F、G、H分别是矩形的边AB、BC、CD、AD上的点,,,,.若,.则四边形EFGH的周长为( )
A. B. C. D.
5.如图,在四边形中,,与交于点,则的值是( )
A. B. C. D.
6.如图,在四边形中(),,把沿着翻折得到.若,则线段的长度为( )
A. B. C. D.
7.如图,在中,,和关于直线BC对称,连接AD,与BC相交于点O,过点C作,垂足为C,与AD相交于点E.若,,则的值为( )
A. B. C. D.
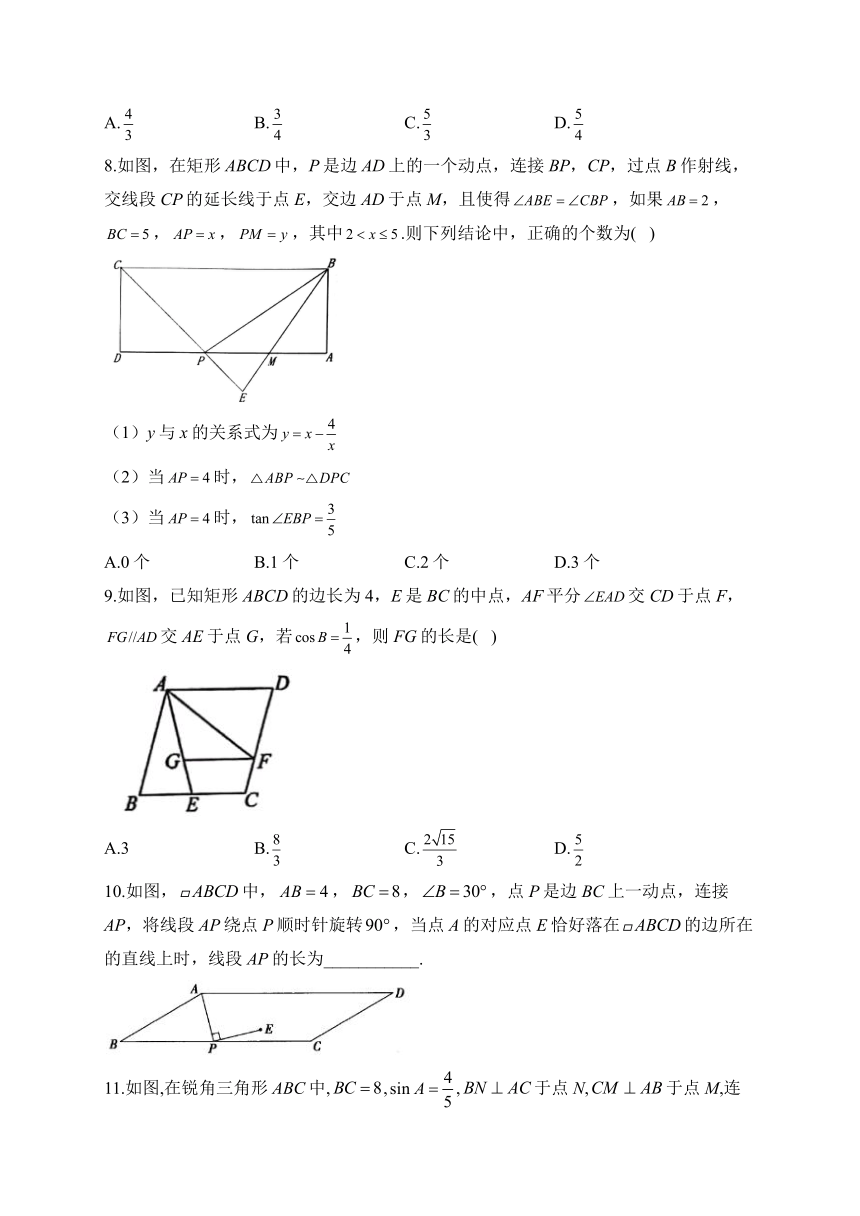
8.如图,在矩形ABCD中,P是边AD上的一个动点,连接BP,CP,过点B作射线,交线段CP的延长线于点E,交边AD于点M,且使得,如果,,,,其中.则下列结论中,正确的个数为( )
(1)y与x的关系式为
(2)当时,
(3)当时,
A.0个 B.1个 C.2个 D.3个
9.如图,已知矩形ABCD的边长为4,E是BC的中点,AF平分交CD于点F,交AE于点G,若,则FG的长是( )
A.3 B. C. D.
10.如图,中,,,,点P是边BC上一动点,连接AP,将线段AP绕点P顺时针旋转,当点A的对应点E恰好落在的边所在的直线上时,线段AP的长为___________.
11.如图,在锐角三角形ABC中,,,于点N,于点M,连接MN,则面积的最大值是______.
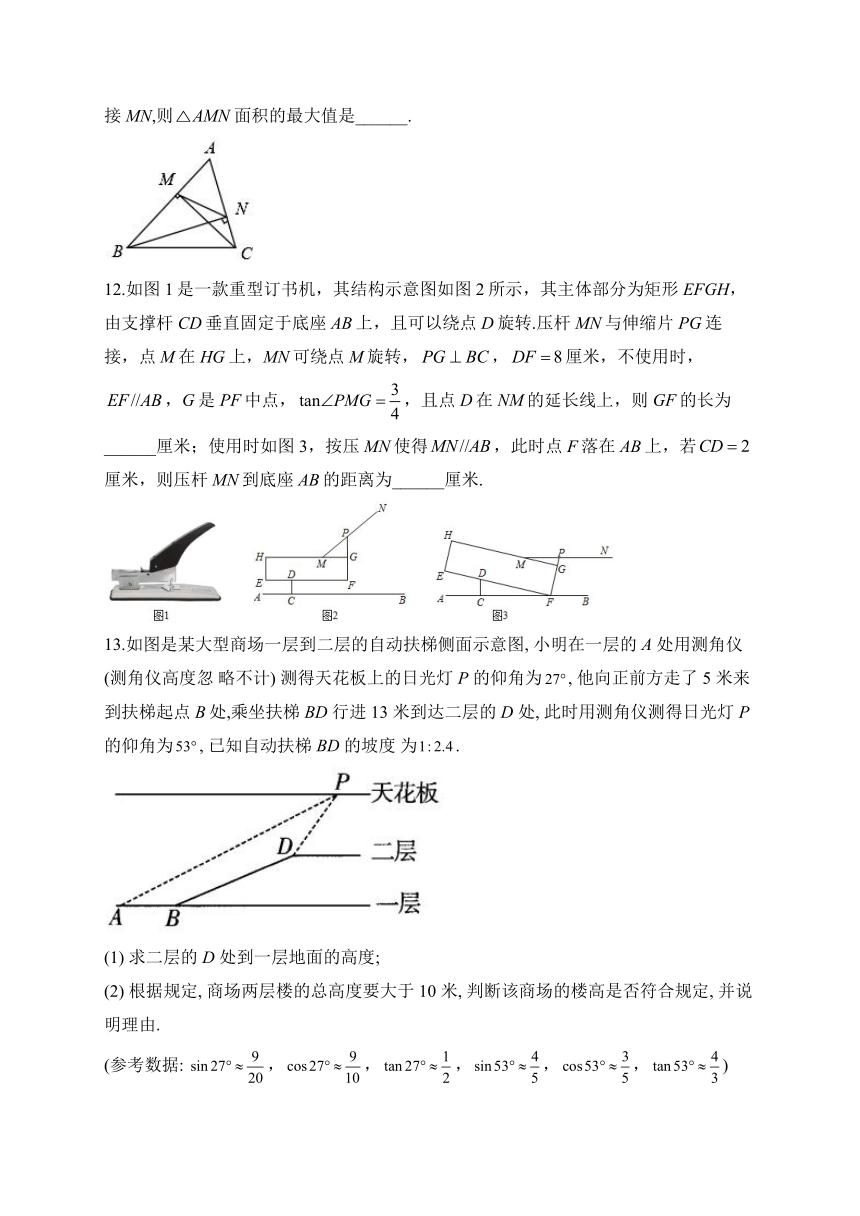
12.如图1是一款重型订书机,其结构示意图如图2所示,其主体部分为矩形EFGH,由支撑杆CD垂直固定于底座AB上,且可以绕点D旋转.压杆MN与伸缩片PG连接,点M在HG上,MN可绕点M旋转,,厘米,不使用时,,G是PF中点,,且点D在NM的延长线上,则GF的长为______厘米;使用时如图3,按压MN使得,此时点F落在AB上,若厘米,则压杆MN到底座AB的距离为______厘米.
13.如图是某大型商场一层到二层的自动扶梯侧面示意图, 小明在一层的A 处用测角仪 (测角仪高度忽 略不计) 测得天花板上的日光灯P 的仰角为, 他向正前方走了 5 米来到扶梯起点 B处,乘坐扶梯BD 行进 13 米到达二层的D 处, 此时用测角仪测得日光灯P 的仰角为, 已知自动扶梯BD 的坡度 为.
(1) 求二层的D 处到一层地面的高度;
(2) 根据规定, 商场两层楼的总高度要大于 10 米, 判断该商场的楼高是否符合规定, 并说明理由.
(参考数据: ,,,,,)
答案以及解析
1.答案:C
解析:如图:在中,,,延长CB到点D,使,连接AD,
设,
,
是的一个外角,
,
,
,
在中,,
,
故选:C.
2.答案:D
解析:如图,连接OC,OD,CD与AB交于点F.
AB是直径,
,
CD平分,
,
,
DE是切圆O切线,
,
,
,
,,
,
,
在中,
,,
,
,,
,,
,
,
,
故选:D.
3.答案:A
解析:连接OC,延长OA、NC交于D,则
,
,
即
,
,
,
的半径为r
,
故选:A.
4.答案:A
解析:如图1,
中,,,,
设,则,,,
,,
如图2,
作于K,作,分别交直线AB于R和T,
四边形ABCD是矩形,
,
在与中,
,
,
,
同理证得,则,
四边形EFGH是平行四边形,
设,则,,,
,
,
,
可得:,
,,
,
,
,
,
,
,
,
,
,
,
,
,
四边形EFGH的周长为:,
故答案为:A.
5.答案:C
解析:.
,
,.在中,.
6.答案:B
解析:如图,延长交于点F,过点D作于点,,,.设,则.
∵在中,,解得,.
7.答案:D
解析:和关于直线BC对称,
,,
,
,
四边形ABDC是菱形,
,,
,,
,
,
,
,
,
,
,
,
,
故选D.
8.答案:C
解析:(1)过点P作于点F,如图,
四边形ABCD是矩形,,
四边形ABFP是矩形,
,,
.
,
,
,
,
.
.
.
(1)的结论正确;
(2)当时,
,
,,
.
,
.
(2)的结论正确;
(3)由(2)知:当时,,
.
,
.
.
.
.
由(1)知:,
,
.
,
.
,
解得:,
,
(3)的结论错误,
综上,正确的结论为:(1)(2),
故选:C.
9.答案:B
解析:如图,过点A作于点H,过点F作于点Q,
菱形ABCD的边长为4,,,,,E是BC的中点,,,AH是BE的垂直平分线,,AF平分,,,,,,设,,,,,,,,,解得,则FG的长是.故选:B.
10.答案:2,4或
解析:分四种情况讨论.①当点E落在BC上时,如图(1),由旋转知,.在中,,,.
②当点E落在CD上时,如图(2),过点A作于点M,过点E作于点N,由旋转知,,易证.易知,,.设,则,.易知,,即,解得,点P与点B重合,.
③当点E落在AD上时,如图(3),过点P作于点F,易知,,,,.
④当点E落在AB上时,过点P作,垂足为G,,,,,,.,点P在线段BC的延长线上,不符合题意.综上,AP的长为2,4或.
11.答案:
解析:,,
,
,,
点M,N在以BC为直径的圆上,
,
和中,,
,
,即,
设,,则,,
,
,
,即,
,即,
,
解得,
,
则面积的最大值是,
故答案为:.
12.答案:3;
解析:如图2,延长NM,则NM过点D,
四边形EFGH是矩形,,
,
,
即,
,
G是PF中点,
厘米,
如图3,过点P作于K,
,
,
,
在中,厘米,
,
,
即,
厘米.
故答案为:3;.
13.答案:(1) 5 米
(2) 该商场的楼高符合规定,理由见解析
解析: (1) 如图, 过点D 作 于点F,
自动扶梯 BD的坡度为,
在中, ,,
,
解得 (负值已舍去).
二层的D 处到一层地面的高度为 5 米.
(2) 该商场的楼高符合规定.
理由: 如图, 过点P 作 于Q点, 交DE 于点M, 则, 且.
易知,
四边形DMQF 是矩形 (依据: 有一个角是直角的平行 四边形是矩形),
,
由题意可知,
设, 则,
,
,
,
由题意可知,
在中, ,
解得,
该商场的楼高符合规定.
1.小明喜欢构建几何图形,利用数形结合的思想解决代数问题在计算时,如图,在中,,,延长CB使,连接AD,得,所以,类比小明的方法,计算的值为( )
A. B. C. D.
2.如图,AB是圆的直径,CD是的平分线交圆O于点D,过D作圆O的切线交CB的延长线于点E.若,,则CD的长为( )
A. B.2 C. D.
3.如图,已知扇形OAB的半径为r,C是弧AB上的任一点(不与A,B重合),,垂足为M,,垂足为N,连接MN,若,则MN可用表示为( )
A. B. C. D.
4.如图,E、F、G、H分别是矩形的边AB、BC、CD、AD上的点,,,,.若,.则四边形EFGH的周长为( )
A. B. C. D.
5.如图,在四边形中,,与交于点,则的值是( )
A. B. C. D.
6.如图,在四边形中(),,把沿着翻折得到.若,则线段的长度为( )
A. B. C. D.
7.如图,在中,,和关于直线BC对称,连接AD,与BC相交于点O,过点C作,垂足为C,与AD相交于点E.若,,则的值为( )
A. B. C. D.
8.如图,在矩形ABCD中,P是边AD上的一个动点,连接BP,CP,过点B作射线,交线段CP的延长线于点E,交边AD于点M,且使得,如果,,,,其中.则下列结论中,正确的个数为( )
(1)y与x的关系式为
(2)当时,
(3)当时,
A.0个 B.1个 C.2个 D.3个
9.如图,已知矩形ABCD的边长为4,E是BC的中点,AF平分交CD于点F,交AE于点G,若,则FG的长是( )
A.3 B. C. D.
10.如图,中,,,,点P是边BC上一动点,连接AP,将线段AP绕点P顺时针旋转,当点A的对应点E恰好落在的边所在的直线上时,线段AP的长为___________.
11.如图,在锐角三角形ABC中,,,于点N,于点M,连接MN,则面积的最大值是______.
12.如图1是一款重型订书机,其结构示意图如图2所示,其主体部分为矩形EFGH,由支撑杆CD垂直固定于底座AB上,且可以绕点D旋转.压杆MN与伸缩片PG连接,点M在HG上,MN可绕点M旋转,,厘米,不使用时,,G是PF中点,,且点D在NM的延长线上,则GF的长为______厘米;使用时如图3,按压MN使得,此时点F落在AB上,若厘米,则压杆MN到底座AB的距离为______厘米.
13.如图是某大型商场一层到二层的自动扶梯侧面示意图, 小明在一层的A 处用测角仪 (测角仪高度忽 略不计) 测得天花板上的日光灯P 的仰角为, 他向正前方走了 5 米来到扶梯起点 B处,乘坐扶梯BD 行进 13 米到达二层的D 处, 此时用测角仪测得日光灯P 的仰角为, 已知自动扶梯BD 的坡度 为.
(1) 求二层的D 处到一层地面的高度;
(2) 根据规定, 商场两层楼的总高度要大于 10 米, 判断该商场的楼高是否符合规定, 并说明理由.
(参考数据: ,,,,,)
答案以及解析
1.答案:C
解析:如图:在中,,,延长CB到点D,使,连接AD,
设,
,
是的一个外角,
,
,
,
在中,,
,
故选:C.
2.答案:D
解析:如图,连接OC,OD,CD与AB交于点F.
AB是直径,
,
CD平分,
,
,
DE是切圆O切线,
,
,
,
,,
,
,
在中,
,,
,
,,
,,
,
,
,
故选:D.
3.答案:A
解析:连接OC,延长OA、NC交于D,则
,
,
即
,
,
,
的半径为r
,
故选:A.
4.答案:A
解析:如图1,
中,,,,
设,则,,,
,,
如图2,
作于K,作,分别交直线AB于R和T,
四边形ABCD是矩形,
,
在与中,
,
,
,
同理证得,则,
四边形EFGH是平行四边形,
设,则,,,
,
,
,
可得:,
,,
,
,
,
,
,
,
,
,
,
,
,
,
四边形EFGH的周长为:,
故答案为:A.
5.答案:C
解析:.
,
,.在中,.
6.答案:B
解析:如图,延长交于点F,过点D作于点,,,.设,则.
∵在中,,解得,.
7.答案:D
解析:和关于直线BC对称,
,,
,
,
四边形ABDC是菱形,
,,
,,
,
,
,
,
,
,
,
,
,
故选D.
8.答案:C
解析:(1)过点P作于点F,如图,
四边形ABCD是矩形,,
四边形ABFP是矩形,
,,
.
,
,
,
,
.
.
.
(1)的结论正确;
(2)当时,
,
,,
.
,
.
(2)的结论正确;
(3)由(2)知:当时,,
.
,
.
.
.
.
由(1)知:,
,
.
,
.
,
解得:,
,
(3)的结论错误,
综上,正确的结论为:(1)(2),
故选:C.
9.答案:B
解析:如图,过点A作于点H,过点F作于点Q,
菱形ABCD的边长为4,,,,,E是BC的中点,,,AH是BE的垂直平分线,,AF平分,,,,,,设,,,,,,,,,解得,则FG的长是.故选:B.
10.答案:2,4或
解析:分四种情况讨论.①当点E落在BC上时,如图(1),由旋转知,.在中,,,.
②当点E落在CD上时,如图(2),过点A作于点M,过点E作于点N,由旋转知,,易证.易知,,.设,则,.易知,,即,解得,点P与点B重合,.
③当点E落在AD上时,如图(3),过点P作于点F,易知,,,,.
④当点E落在AB上时,过点P作,垂足为G,,,,,,.,点P在线段BC的延长线上,不符合题意.综上,AP的长为2,4或.
11.答案:
解析:,,
,
,,
点M,N在以BC为直径的圆上,
,
和中,,
,
,即,
设,,则,,
,
,
,即,
,即,
,
解得,
,
则面积的最大值是,
故答案为:.
12.答案:3;
解析:如图2,延长NM,则NM过点D,
四边形EFGH是矩形,,
,
,
即,
,
G是PF中点,
厘米,
如图3,过点P作于K,
,
,
,
在中,厘米,
,
,
即,
厘米.
故答案为:3;.
13.答案:(1) 5 米
(2) 该商场的楼高符合规定,理由见解析
解析: (1) 如图, 过点D 作 于点F,
自动扶梯 BD的坡度为,
在中, ,,
,
解得 (负值已舍去).
二层的D 处到一层地面的高度为 5 米.
(2) 该商场的楼高符合规定.
理由: 如图, 过点P 作 于Q点, 交DE 于点M, 则, 且.
易知,
四边形DMQF 是矩形 (依据: 有一个角是直角的平行 四边形是矩形),
,
由题意可知,
设, 则,
,
,
,
由题意可知,
在中, ,
解得,
该商场的楼高符合规定.
