2.2 二次函数的图象与性质第3课时 同步课件(共32张PPT)
文档属性
| 名称 | 2.2 二次函数的图象与性质第3课时 同步课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 872.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 07:37:32 | ||
图片预览



文档简介
(共32张PPT)
北师大版 数学 九年级下册
第3课时
第二章 二次函数
2 二次函数的图象与性质
学习目标
1.能够画出函数y=a(x-h)2和函数y=a(x-h)2+k的图象,并能理解它们与y=ax2的图象的关系,理解a,h和k对二次函数图象的影响.(重点)2.能正确说出y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标.3.探索函数y=a(x-h)2和函数y=a(x-h)2+k的图象与二次函数y=ax2的图象的关系,理解抛物线的平移规律.(难点)
复习回顾
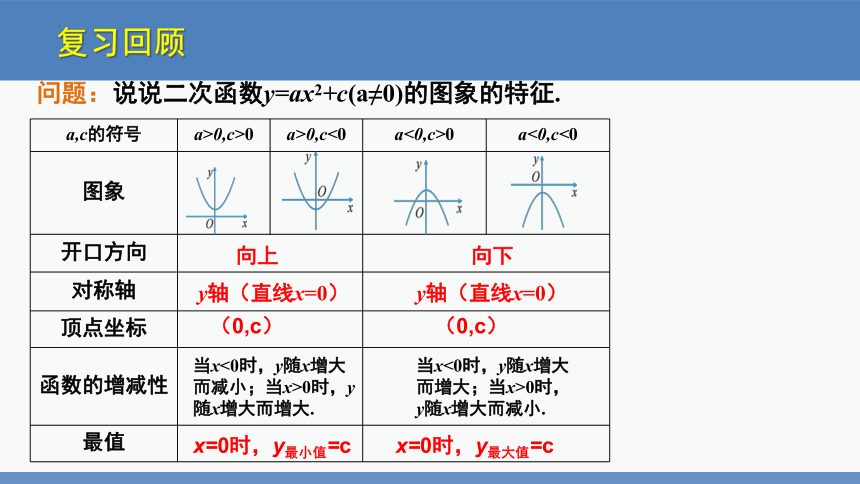
a,c的符号 a>0,c>0 a>0,c<0 a<0,c>0 a<0,c<0
图象
开口方向
对称轴
顶点坐标
函数的增减性
最值
向上
向下
y轴(直线x=0)
y轴(直线x=0)
(0,c)
(0,c)
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
x=0时,y最小值=c
x=0时,y最大值=c
问题:说说二次函数y=ax2+c(a≠0)的图象的特征.
一、创设情境,引入新知
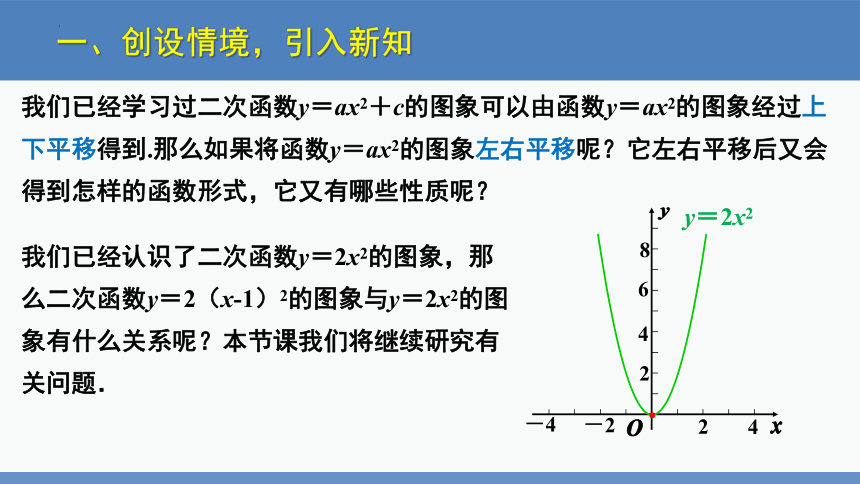
我们已经学习过二次函数y=ax2+c的图象可以由函数y=ax2的图象经过上下平移得到.那么如果将函数y=ax2的图象左右平移呢?它左右平移后又会得到怎样的函数形式,它又有哪些性质呢?
我们已经认识了二次函数y=2x2的图象,那么二次函数y=2(x-1)2的图象与y=2x2的图象有什么关系呢?本节课我们将继续研究有关问题.
x
y
O
-2
2
2
4
6
4
-4
8
y=2x2
二、自主合作,探究新知
探究一:二次函数y=a(x-h)2的图象和性质
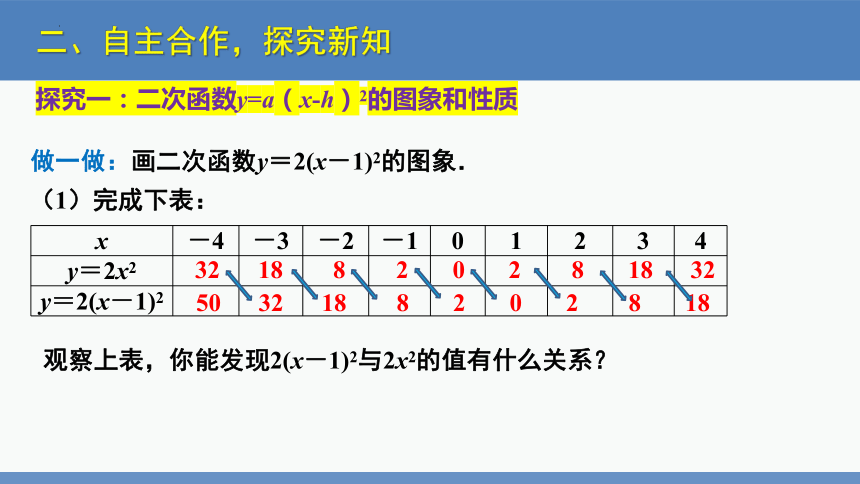
做一做:画二次函数y=2(x-1)2的图象.
(1)完成下表:
x -4 -3 -2 -1 0 1 2 3 4
y=2x2
y=2(x-1)2
观察上表,你能发现2(x-1)2与2x2的值有什么关系?
32 18 8 2 0 2 8 18 32
50 32 18 8 2 0 2 8 18
二、自主合作,探究新知
O
x
y
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–3
–2
–1
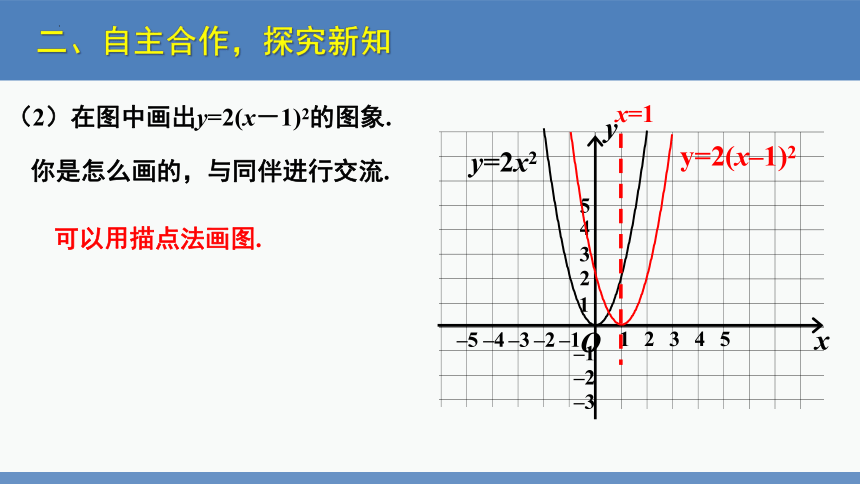
y=2x2
y=2(x–1)2
你是怎么画的,与同伴进行交流.
(2)在图中画出y=2(x-1)2的图象.
可以用描点法画图.
x=1
二、自主合作,探究新知
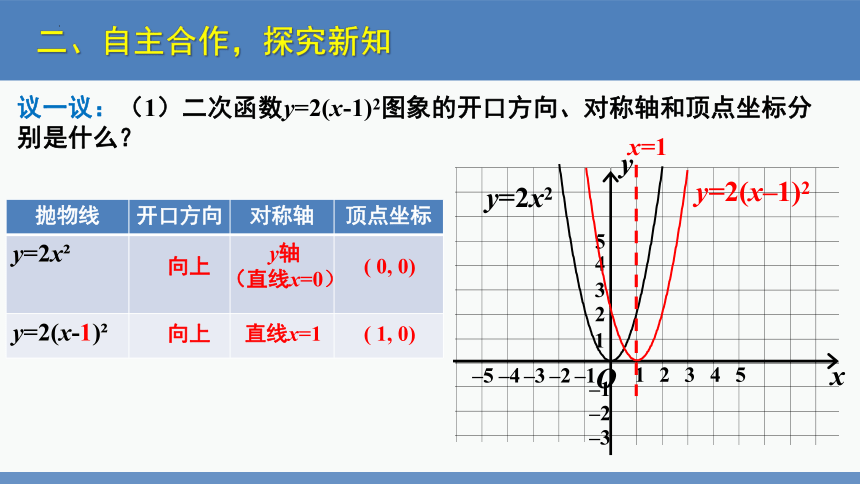
议一议:(1)二次函数y=2(x-1)2图象的开口方向、对称轴和顶点坐标分别是什么?
O
x
y
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–3
–2
–1
y=2x2
y=2(x–1)2
x=1
抛物线 开口方向 对称轴 顶点坐标
y=2x
y=2(x-1)
向上
向上
y轴
(直线x=0)
直线x=1
( 0, 0)
( 1, 0)
二、自主合作,探究新知
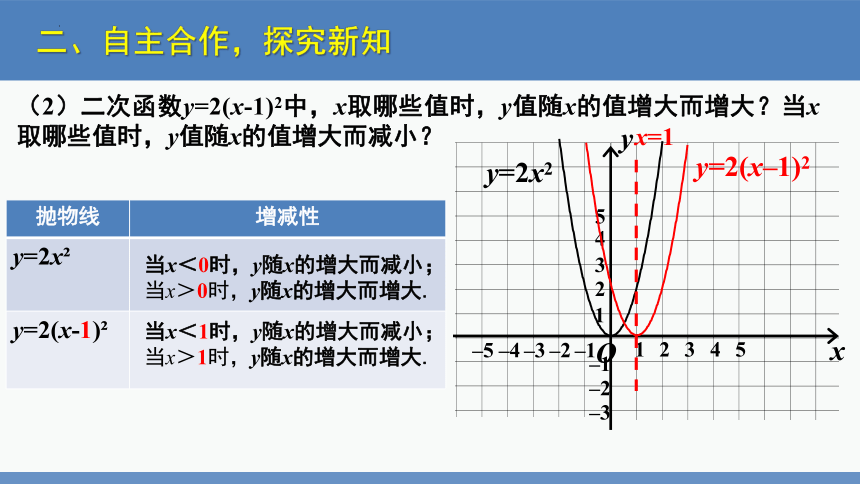
(2)二次函数y=2(x-1)2中,x取哪些值时,y值随x的值增大而增大?当x取哪些值时,y值随x的值增大而减小?
抛物线 增减性
y=2x
y=2(x-1)
当x<0时,y随x的增大而减小;
当x>0时,y随x的增大而增大.
当x<1时,y随x的增大而减小;
当x>1时,y随x的增大而增大.
O
x
y
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–3
–2
–1
y=2x2
y=2(x–1)2
x=1
二、自主合作,探究新知
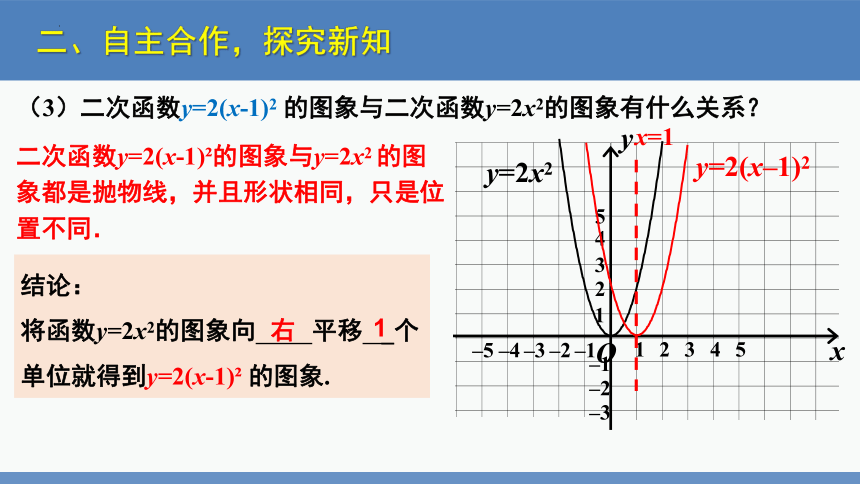
结论:
将函数y=2x2的图象向 平移 _个单位就得到y=2(x-1) 的图象.
右
1
(3)二次函数y=2(x-1)2 的图象与二次函数y=2x2的图象有什么关系?
二次函数y=2(x-1) 的图象与y=2x2 的图象都是抛物线,并且形状相同,只是位置不同.
O
x
y
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–3
–2
–1
y=2x2
y=2(x–1)2
x=1
二、自主合作,探究新知
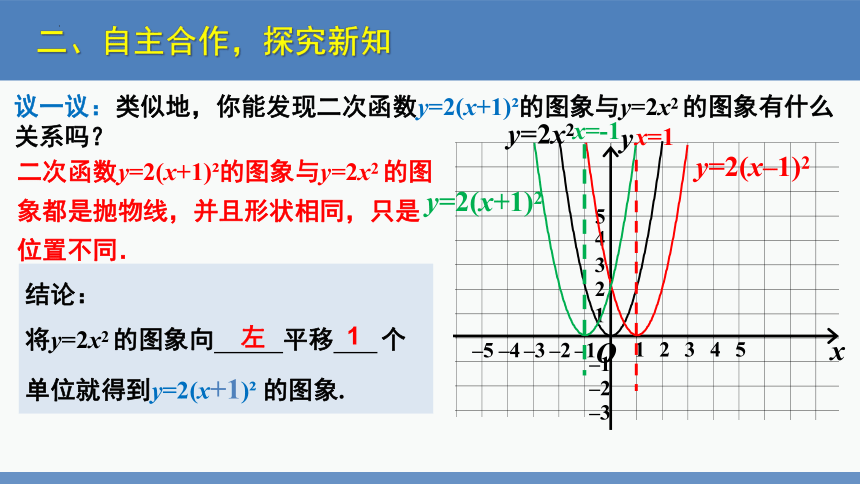
议一议:类似地,你能发现二次函数y=2(x+1) 的图象与y=2x2 的图象有什么关系吗?
结论:
将y=2x2 的图象向 平移 个单位就得到y=2(x+1) 的图象.
左
1
O
x
y
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–3
–2
–1
y=2x2
y=2(x–1)2
y=2(x+1)2
二次函数y=2(x+1) 的图象与y=2x2 的图象都是抛物线,并且形状相同,只是位置不同.
x=1
x=-1
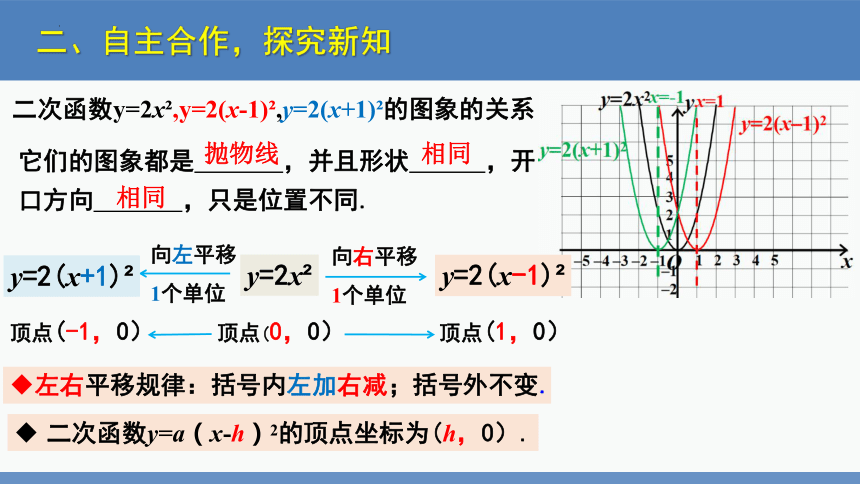
二次函数y=2x ,y=2(x-1) ,y=2(x+1) 的图象的关系
二、自主合作,探究新知
向左平移
1个单位
向右平移
1个单位
y=2x
y=2(x-1)
y=2(x+1)
左右平移规律:括号内左加右减;括号外不变.
二次函数y=a(x-h)2的顶点坐标为(h,0).
它们的图象都是 ,并且形状 ,开口方向 ,只是位置不同.
抛物线
相同
相同
顶点(0,0)
顶点(1,0)
顶点(-1,0)
知识要点
二、自主合作,探究新知
二次函数y=a(x-h)2的图象与y=ax2 的图象的关系
可以看作互相平移得到(h>0).
左右平移规律:
括号内左加右减;括号外不变.
当向左平移 ︱h︱ 时
当向右平移 ︱h︱ 时
y=ax2
y=a(x-h)2
y=a(x+h)2
二、自主合作,探究新知
典型例题
例1:抛物线y=-3(x+2)2可以由抛物线y=-3x2向 平移 个单位得到。
它的图象开口向 ,对称轴是 ,顶点坐标 .
当x 时,y随x的增大而增大;
当x 时,y随x的增大而减小.
左
2
下
直线x=-2
(-2,0)
<-2
>-2
二、自主合作,探究新知
开口 对称轴 顶点 最值 增减性
x>h xa>0
a<0
向上
x=h
(h,0)
y随x的增大而增大
y随x的增大而减小
当x=h时,
向下
x=h
(h,0)
当x=h时,
y随x的增大而减小
y随x的增大而增大
二次函数 y=a(x-h)2的性质
知识要点
顶点(-3,0)
顶点(-3,)
顶点(0,0)
二、自主合作,探究新知
探究二:二次函数y=a(x-h)2+k的图象和性质
向左平移3个单位
y=2x2
y=2(x+3)2
向下平移个单位
想一想:由二次函数y=2x 的图象,你能得到二次函数的图象吗?你是怎样得到的?与同伴进行交流.
平移方法1
向左平移3个单位
向下平移个单位
顶点(0,)
顶点(-3,)
顶点(0,0)
二、自主合作,探究新知
y=2x2
向下平移个单位
向左平移3个单位
平移方法2
向下平移个单位
向左平移3个单位
y=2x2
二、自主合作,探究新知
议一议:二次函数y=a(x-h)2+k与y=ax2的图象有什么关系?
一般地,平移二次函数y=ax2的图象便可得到二次函数y=a (x-h)2+k的图象.因此,二次函数y=a (x-h)2+k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标与a,h, k的值有关.
y=a (x-h)2+k 开口方向 对称轴 顶点坐标
a>0
a<0
向上
直线x=h
(h,k)
向下
直线x=h
(h,k)
二、自主合作,探究新知
二次函数y=ax2 (a≠0)与y=a(x-h)2+k(a≠0)的关系
y = ax2(a≠0)
y = a( x - h )2 + k(a≠0)
平移规律简记为:
上下平移,括号外上加下减;左右平移,括号内左加右减.
二次项系数a不变.
顶点(0,0)
顶点(h,k)
顶点式
知识要点
例2:若将抛物线y=x2+1先向左平移2个单位,再向下平移3个单位,那么所得抛物线的函数关系式是( ).
A.y=(x+2)2+2 B.y=(x+2)2-2
C.y=(x-2)2+2 D.y=(x-2)2-2
二、自主合作,探究新知
B
典型例题
二、自主合作,探究新知
二次函数 y=a(x-h)2+k的性质
y=a(x-h)2+k a>0 a<0
开口方向
对称轴
顶点坐标
最值
增减性
向上
向下
直线x=h
(h,k)
当x=h时,ymin=k
当x=h时,ymax=k
当x<h时,y随x的增大而减小;
当x>h时,y随x的增大而增大.
当x<h时,y随x的增大而增大.
当x>h时,y随x的增大而减小;
知识要点
二、自主合作,探究新知
例3:对于抛物线y=-(x+1)2+3,下列结论:
① 抛物线的开口向下;② 对称轴为直线x=1;
③ 顶点坐标为(-1,3);④ x>1 时,y 随x 的增大而减小.
其中正确结论有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
C
典型例题
分析:①∵ a=-1<0,∴抛物线的开口向下,正确;
②对称轴为直线x=-1,错误;
③顶点坐标为(-1,3),正确;
④ x>1 时,y 随x 的增大而减小,正确.
综上所述,结论正确的是①③④,共3 个,故选C.
1.对于抛物线 的说法错误的是( ).
A.抛物线的开口向下
B.抛物线的顶点坐标是(1,0)
C.抛物线的对称轴是直线x=1
D.当x>1时,y随x的增大而增大
三、即学即练,应用知识
2. 将二次函数y=-2x2的图象平移后,可得到二次函数y=-2(x+1)2的图象,平移的方法是( )
A.向上平移1个单位 B.向下平移1个单位
C.向左平移1个单位 D.向右平移1个单位
C
D
4.将抛物线 向左平移2个单位后,其顶点坐标为( )
A.(-3,-2) B.(-2,0) C.(-5,0) D.(-3,0)
C
3.对于抛物线y=- (x 2)2+6,下列结论:①抛物线的开口向下;②对称轴为直线x=2;③顶点坐标为(2,6);④当x>2时,y随x的增大而减小.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
D
三、即学即练,应用知识
5.抛物线 的对称轴是________ ,顶点坐标是________;当x>2时,y随x的增大而_______;当x<2时,y随x的增大而_______;当x=______时,函数有_____值,其值为_______.
三、即学即练,应用知识
直线x=2
(2,7)
减小
增大
2
最大
7
6.抛物线y=a(x-h)2+k与抛物线y=-2x2的形状相同,开口方向相同,其顶点坐标为(-1,3)此抛物线的解析式为__________________.
y=-2(x+1)2+3
8.已知y= (x-3)2-2的部分图象如图所示,抛物线与x轴交点的一个坐标是(1,0),则另一个交点的坐标是________.
三、即学即练,应用知识
(5,0)
7.已知点A(x1,y1)、B(x2,y2)在二次函数y= -(x-1)2+1的图象上,若-1<x1<0,3<x2<4,则y1_____y2(填“>”、“<”或“=”).
>
三、即学即练,应用知识
解:(1)抛物线y=-(x+1)2+3的顶点坐标为(-1,3),把点(-1,3)先向右平移2个单位长度,再向下平移4个单位长度得到点(1,-1),
∴原二次函数的表达式为y=-(x-1)2-1,
∴a=-,h=1,k=-1.
(2)∵y=a(x-h)2+k=-(x-1)2-1,
∴ 图象的开口方向向下,对称轴为直线x=1,顶点坐标为(1,-1).
9.已知将二次函数y=a(x-h)2+k的图象先向左平移2个单位长度,再向上平移4个单位长度,得到抛物线y=-(x+1)2+3.(1)试确定a、h、k的值;(2)指出二次函数y=a(x-h)2+k图象的开口方向、对称轴和顶点坐标.
四、课堂小结
平移规律
二次函数y=a(x-h)2+k的图象和性质
左右平移:括号内左加右减;
上下平移:括号外上加下减.
y=a(x-h)2+k a>0 a<0
开口方向
对称轴
顶点坐标
最值
增减性
向上
向下
直线x=h
(h,k)
当x=h时,ymin=k
当x=h时,ymax=k
当x<h时,y随x的增大而减小;
当x>h时,y随x的增大而增大.
当x<h时,y随x的增大而增大.
当x>h时,y随x的增大而减小;
1.将抛物线 沿x轴向左平移2个单位,再沿y轴向下平移3个单位得到抛物线( ).
A. B.
C. D.
2.由二次函数y=2(x-3)2+1,可知( ).
A.其图象的开口向下 B.其图象的对称轴为直线x=-3
C.其最小值为1 D.当x<3时,y随x的增大而增大
五、当堂达标检测
B
C
3.对于抛物线y=(x 2)2+6,下列结论:
①抛物线的开口向下; ②对称轴为直线x=2;
③顶点坐标为(2,6); ④当x>2时,y随x的增大而减小.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
五、当堂达标检测
D
4.抛物线y=2x2先向左平移1个单位,再向上平移3个单位,得到的抛物线解析式为 ;
五、当堂达标检测
二次函数 开口方向 对称轴 顶点坐标
y=2(x+3)2+5
向上
( 1, -2 )
向下
向下
( 3 , 7)
( 2 , -6 )
向上
直线x=-3
直线x=1
直线x=3
直线x=2
(-3, 5 )
y=-3(x-1)2-2
y = 4(x-3)2+7
y=-5(2-x)2-6
5.完成下列表格:
6.函数y=5(x-3)2-2的图象可由函数y=5x2的图象先向 平移 个单位,再向 平移 个单位得到;
右
下
2
3
因此抛物线的解析式为:
y= (x-1)2+3 (0≤x≤3)
3
4
-
五、当堂达标检测
7.要修建一个圆形喷水池,在池中心竖直安装一根水管.在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长
B(1,3)
A
x
O
y
1
2
3
1
2
3
解:如图建立直角坐标系,点(1,3)是图中这段抛物线的顶点.
因此可设这段抛物线对应的函数是y=a(x-1)2+3 (0≤x≤3).
当x=0时,y=2.25.
答:水管长应为2.25m.
∵这段抛物线经过点(3,0),
∴ 0=a(3-1)2+3.
解得:a=
教材习题2.4;
六、布置作业
北师大版 数学 九年级下册
第3课时
第二章 二次函数
2 二次函数的图象与性质
学习目标
1.能够画出函数y=a(x-h)2和函数y=a(x-h)2+k的图象,并能理解它们与y=ax2的图象的关系,理解a,h和k对二次函数图象的影响.(重点)2.能正确说出y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标.3.探索函数y=a(x-h)2和函数y=a(x-h)2+k的图象与二次函数y=ax2的图象的关系,理解抛物线的平移规律.(难点)
复习回顾
a,c的符号 a>0,c>0 a>0,c<0 a<0,c>0 a<0,c<0
图象
开口方向
对称轴
顶点坐标
函数的增减性
最值
向上
向下
y轴(直线x=0)
y轴(直线x=0)
(0,c)
(0,c)
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
x=0时,y最小值=c
x=0时,y最大值=c
问题:说说二次函数y=ax2+c(a≠0)的图象的特征.
一、创设情境,引入新知
我们已经学习过二次函数y=ax2+c的图象可以由函数y=ax2的图象经过上下平移得到.那么如果将函数y=ax2的图象左右平移呢?它左右平移后又会得到怎样的函数形式,它又有哪些性质呢?
我们已经认识了二次函数y=2x2的图象,那么二次函数y=2(x-1)2的图象与y=2x2的图象有什么关系呢?本节课我们将继续研究有关问题.
x
y
O
-2
2
2
4
6
4
-4
8
y=2x2
二、自主合作,探究新知
探究一:二次函数y=a(x-h)2的图象和性质
做一做:画二次函数y=2(x-1)2的图象.
(1)完成下表:
x -4 -3 -2 -1 0 1 2 3 4
y=2x2
y=2(x-1)2
观察上表,你能发现2(x-1)2与2x2的值有什么关系?
32 18 8 2 0 2 8 18 32
50 32 18 8 2 0 2 8 18
二、自主合作,探究新知
O
x
y
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–3
–2
–1
y=2x2
y=2(x–1)2
你是怎么画的,与同伴进行交流.
(2)在图中画出y=2(x-1)2的图象.
可以用描点法画图.
x=1
二、自主合作,探究新知
议一议:(1)二次函数y=2(x-1)2图象的开口方向、对称轴和顶点坐标分别是什么?
O
x
y
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–3
–2
–1
y=2x2
y=2(x–1)2
x=1
抛物线 开口方向 对称轴 顶点坐标
y=2x
y=2(x-1)
向上
向上
y轴
(直线x=0)
直线x=1
( 0, 0)
( 1, 0)
二、自主合作,探究新知
(2)二次函数y=2(x-1)2中,x取哪些值时,y值随x的值增大而增大?当x取哪些值时,y值随x的值增大而减小?
抛物线 增减性
y=2x
y=2(x-1)
当x<0时,y随x的增大而减小;
当x>0时,y随x的增大而增大.
当x<1时,y随x的增大而减小;
当x>1时,y随x的增大而增大.
O
x
y
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–3
–2
–1
y=2x2
y=2(x–1)2
x=1
二、自主合作,探究新知
结论:
将函数y=2x2的图象向 平移 _个单位就得到y=2(x-1) 的图象.
右
1
(3)二次函数y=2(x-1)2 的图象与二次函数y=2x2的图象有什么关系?
二次函数y=2(x-1) 的图象与y=2x2 的图象都是抛物线,并且形状相同,只是位置不同.
O
x
y
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–3
–2
–1
y=2x2
y=2(x–1)2
x=1
二、自主合作,探究新知
议一议:类似地,你能发现二次函数y=2(x+1) 的图象与y=2x2 的图象有什么关系吗?
结论:
将y=2x2 的图象向 平移 个单位就得到y=2(x+1) 的图象.
左
1
O
x
y
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–3
–2
–1
y=2x2
y=2(x–1)2
y=2(x+1)2
二次函数y=2(x+1) 的图象与y=2x2 的图象都是抛物线,并且形状相同,只是位置不同.
x=1
x=-1
二次函数y=2x ,y=2(x-1) ,y=2(x+1) 的图象的关系
二、自主合作,探究新知
向左平移
1个单位
向右平移
1个单位
y=2x
y=2(x-1)
y=2(x+1)
左右平移规律:括号内左加右减;括号外不变.
二次函数y=a(x-h)2的顶点坐标为(h,0).
它们的图象都是 ,并且形状 ,开口方向 ,只是位置不同.
抛物线
相同
相同
顶点(0,0)
顶点(1,0)
顶点(-1,0)
知识要点
二、自主合作,探究新知
二次函数y=a(x-h)2的图象与y=ax2 的图象的关系
可以看作互相平移得到(h>0).
左右平移规律:
括号内左加右减;括号外不变.
当向左平移 ︱h︱ 时
当向右平移 ︱h︱ 时
y=ax2
y=a(x-h)2
y=a(x+h)2
二、自主合作,探究新知
典型例题
例1:抛物线y=-3(x+2)2可以由抛物线y=-3x2向 平移 个单位得到。
它的图象开口向 ,对称轴是 ,顶点坐标 .
当x 时,y随x的增大而增大;
当x 时,y随x的增大而减小.
左
2
下
直线x=-2
(-2,0)
<-2
>-2
二、自主合作,探究新知
开口 对称轴 顶点 最值 增减性
x>h x
a<0
向上
x=h
(h,0)
y随x的增大而增大
y随x的增大而减小
当x=h时,
向下
x=h
(h,0)
当x=h时,
y随x的增大而减小
y随x的增大而增大
二次函数 y=a(x-h)2的性质
知识要点
顶点(-3,0)
顶点(-3,)
顶点(0,0)
二、自主合作,探究新知
探究二:二次函数y=a(x-h)2+k的图象和性质
向左平移3个单位
y=2x2
y=2(x+3)2
向下平移个单位
想一想:由二次函数y=2x 的图象,你能得到二次函数的图象吗?你是怎样得到的?与同伴进行交流.
平移方法1
向左平移3个单位
向下平移个单位
顶点(0,)
顶点(-3,)
顶点(0,0)
二、自主合作,探究新知
y=2x2
向下平移个单位
向左平移3个单位
平移方法2
向下平移个单位
向左平移3个单位
y=2x2
二、自主合作,探究新知
议一议:二次函数y=a(x-h)2+k与y=ax2的图象有什么关系?
一般地,平移二次函数y=ax2的图象便可得到二次函数y=a (x-h)2+k的图象.因此,二次函数y=a (x-h)2+k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标与a,h, k的值有关.
y=a (x-h)2+k 开口方向 对称轴 顶点坐标
a>0
a<0
向上
直线x=h
(h,k)
向下
直线x=h
(h,k)
二、自主合作,探究新知
二次函数y=ax2 (a≠0)与y=a(x-h)2+k(a≠0)的关系
y = ax2(a≠0)
y = a( x - h )2 + k(a≠0)
平移规律简记为:
上下平移,括号外上加下减;左右平移,括号内左加右减.
二次项系数a不变.
顶点(0,0)
顶点(h,k)
顶点式
知识要点
例2:若将抛物线y=x2+1先向左平移2个单位,再向下平移3个单位,那么所得抛物线的函数关系式是( ).
A.y=(x+2)2+2 B.y=(x+2)2-2
C.y=(x-2)2+2 D.y=(x-2)2-2
二、自主合作,探究新知
B
典型例题
二、自主合作,探究新知
二次函数 y=a(x-h)2+k的性质
y=a(x-h)2+k a>0 a<0
开口方向
对称轴
顶点坐标
最值
增减性
向上
向下
直线x=h
(h,k)
当x=h时,ymin=k
当x=h时,ymax=k
当x<h时,y随x的增大而减小;
当x>h时,y随x的增大而增大.
当x<h时,y随x的增大而增大.
当x>h时,y随x的增大而减小;
知识要点
二、自主合作,探究新知
例3:对于抛物线y=-(x+1)2+3,下列结论:
① 抛物线的开口向下;② 对称轴为直线x=1;
③ 顶点坐标为(-1,3);④ x>1 时,y 随x 的增大而减小.
其中正确结论有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
C
典型例题
分析:①∵ a=-1<0,∴抛物线的开口向下,正确;
②对称轴为直线x=-1,错误;
③顶点坐标为(-1,3),正确;
④ x>1 时,y 随x 的增大而减小,正确.
综上所述,结论正确的是①③④,共3 个,故选C.
1.对于抛物线 的说法错误的是( ).
A.抛物线的开口向下
B.抛物线的顶点坐标是(1,0)
C.抛物线的对称轴是直线x=1
D.当x>1时,y随x的增大而增大
三、即学即练,应用知识
2. 将二次函数y=-2x2的图象平移后,可得到二次函数y=-2(x+1)2的图象,平移的方法是( )
A.向上平移1个单位 B.向下平移1个单位
C.向左平移1个单位 D.向右平移1个单位
C
D
4.将抛物线 向左平移2个单位后,其顶点坐标为( )
A.(-3,-2) B.(-2,0) C.(-5,0) D.(-3,0)
C
3.对于抛物线y=- (x 2)2+6,下列结论:①抛物线的开口向下;②对称轴为直线x=2;③顶点坐标为(2,6);④当x>2时,y随x的增大而减小.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
D
三、即学即练,应用知识
5.抛物线 的对称轴是________ ,顶点坐标是________;当x>2时,y随x的增大而_______;当x<2时,y随x的增大而_______;当x=______时,函数有_____值,其值为_______.
三、即学即练,应用知识
直线x=2
(2,7)
减小
增大
2
最大
7
6.抛物线y=a(x-h)2+k与抛物线y=-2x2的形状相同,开口方向相同,其顶点坐标为(-1,3)此抛物线的解析式为__________________.
y=-2(x+1)2+3
8.已知y= (x-3)2-2的部分图象如图所示,抛物线与x轴交点的一个坐标是(1,0),则另一个交点的坐标是________.
三、即学即练,应用知识
(5,0)
7.已知点A(x1,y1)、B(x2,y2)在二次函数y= -(x-1)2+1的图象上,若-1<x1<0,3<x2<4,则y1_____y2(填“>”、“<”或“=”).
>
三、即学即练,应用知识
解:(1)抛物线y=-(x+1)2+3的顶点坐标为(-1,3),把点(-1,3)先向右平移2个单位长度,再向下平移4个单位长度得到点(1,-1),
∴原二次函数的表达式为y=-(x-1)2-1,
∴a=-,h=1,k=-1.
(2)∵y=a(x-h)2+k=-(x-1)2-1,
∴ 图象的开口方向向下,对称轴为直线x=1,顶点坐标为(1,-1).
9.已知将二次函数y=a(x-h)2+k的图象先向左平移2个单位长度,再向上平移4个单位长度,得到抛物线y=-(x+1)2+3.(1)试确定a、h、k的值;(2)指出二次函数y=a(x-h)2+k图象的开口方向、对称轴和顶点坐标.
四、课堂小结
平移规律
二次函数y=a(x-h)2+k的图象和性质
左右平移:括号内左加右减;
上下平移:括号外上加下减.
y=a(x-h)2+k a>0 a<0
开口方向
对称轴
顶点坐标
最值
增减性
向上
向下
直线x=h
(h,k)
当x=h时,ymin=k
当x=h时,ymax=k
当x<h时,y随x的增大而减小;
当x>h时,y随x的增大而增大.
当x<h时,y随x的增大而增大.
当x>h时,y随x的增大而减小;
1.将抛物线 沿x轴向左平移2个单位,再沿y轴向下平移3个单位得到抛物线( ).
A. B.
C. D.
2.由二次函数y=2(x-3)2+1,可知( ).
A.其图象的开口向下 B.其图象的对称轴为直线x=-3
C.其最小值为1 D.当x<3时,y随x的增大而增大
五、当堂达标检测
B
C
3.对于抛物线y=(x 2)2+6,下列结论:
①抛物线的开口向下; ②对称轴为直线x=2;
③顶点坐标为(2,6); ④当x>2时,y随x的增大而减小.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
五、当堂达标检测
D
4.抛物线y=2x2先向左平移1个单位,再向上平移3个单位,得到的抛物线解析式为 ;
五、当堂达标检测
二次函数 开口方向 对称轴 顶点坐标
y=2(x+3)2+5
向上
( 1, -2 )
向下
向下
( 3 , 7)
( 2 , -6 )
向上
直线x=-3
直线x=1
直线x=3
直线x=2
(-3, 5 )
y=-3(x-1)2-2
y = 4(x-3)2+7
y=-5(2-x)2-6
5.完成下列表格:
6.函数y=5(x-3)2-2的图象可由函数y=5x2的图象先向 平移 个单位,再向 平移 个单位得到;
右
下
2
3
因此抛物线的解析式为:
y= (x-1)2+3 (0≤x≤3)
3
4
-
五、当堂达标检测
7.要修建一个圆形喷水池,在池中心竖直安装一根水管.在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长
B(1,3)
A
x
O
y
1
2
3
1
2
3
解:如图建立直角坐标系,点(1,3)是图中这段抛物线的顶点.
因此可设这段抛物线对应的函数是y=a(x-1)2+3 (0≤x≤3).
当x=0时,y=2.25.
答:水管长应为2.25m.
∵这段抛物线经过点(3,0),
∴ 0=a(3-1)2+3.
解得:a=
教材习题2.4;
六、布置作业
