6.3 数据的表示第2课时 课件(共24张PPT)
文档属性
| 名称 | 6.3 数据的表示第2课时 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
北师大版 数学 七年级上册
第2课时
3 数据的表示
第六章 数据的收集与整理
学习目标
1.了解频数分布直方图;(重点)
2.会从频数分布直方图中获得数据信息;(重点)
3.能够根据已知题目画出频数分布直方图.(重、难点)
1.圆代表 , 圆中的各个扇形分别代表总体中的不同部分, 扇形的大小反映 的大小。 这样的统计图叫做扇形统计图。
排球18%
足球25%
乒乓球32%
篮球19%
其他6%
一、导入新课
复习回顾
(1)计算总体数目。
2.扇形统计图的画法的步骤:
(2)计算各部分占总体的百分比。
(3)计算扇形的圆心角。
(4)画图。
(5)标上百分比。
(6)标上图形的名称。
总体
部分占总体百分比
2.在扇形统计图中,每部分占总体的百分比等于该部分所对应的__________________与________的比.
扇形圆心角的度数
360°
一、导入新课
情境导入
A
A
B
C
D
A
B
A
A
C
B
A
A
C
B
C
A
A
B
C
A
A
B
A
C
D
A
A
C
D
B
A
C
D
A
A
A
C
D
A
C
B
A
A
C
C
D
A
A
C
书籍是人类进步的阶梯,同学们在课外最爱读那一类书籍?
文学类(A)、漫画类(B)科普类(C)、历史类(D)
下面是小亮调查的七(1)班50位同学喜欢的书籍,结果如下:
根据上面结果,你能很快说出该班同学最喜欢读那一类书吗?他的数据表示方式是什么?
这些数据没有经过统计、整理,必须把A、B、C、D的个数全部数清,才能比较出哪类书是该班同学最喜欢的.数据越多越不方便,所以小亮的数据表示方式不太好.
一、导入新课
情境导入
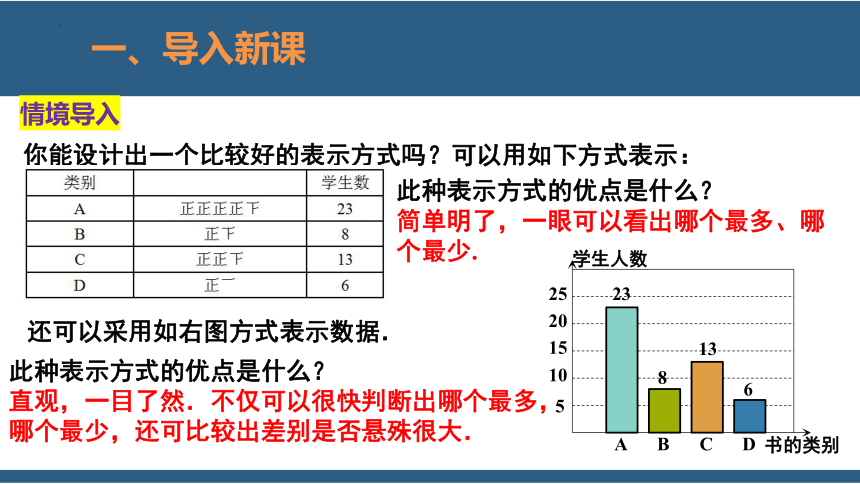
你能设计出一个比较好的表示方式吗?可以用如下方式表示:
此种表示方式的优点是什么?
简单明了,一眼可以看出哪个最多、哪个最少.
此种表示方式的优点是什么?
直观,一目了然.不仅可以很快判断出哪个最多,哪个最少,还可比较出差别是否悬殊很大.
还可以采用如右图方式表示数据.
5
10
15
20
25
A
B
C
D
学生人数
书的类别
23
8
13
6
二、新知探究
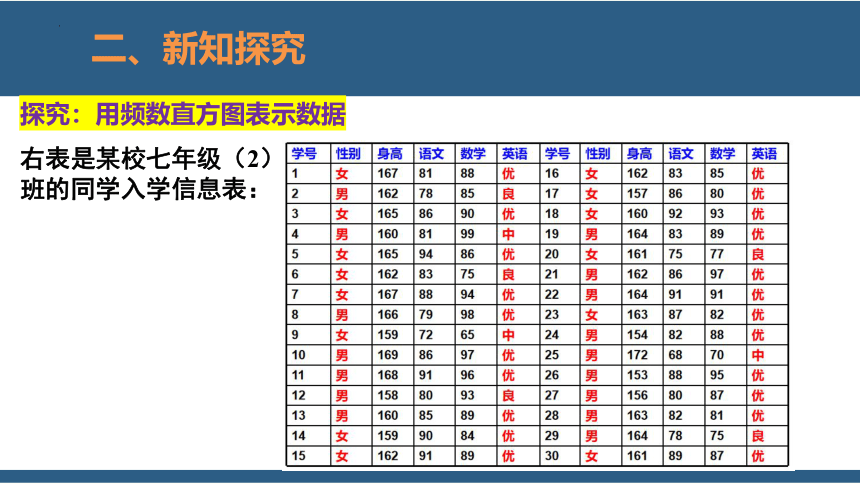
探究:用频数直方图表示数据
右表是某校七年级(2)班的同学入学信息表:
二、新知探究
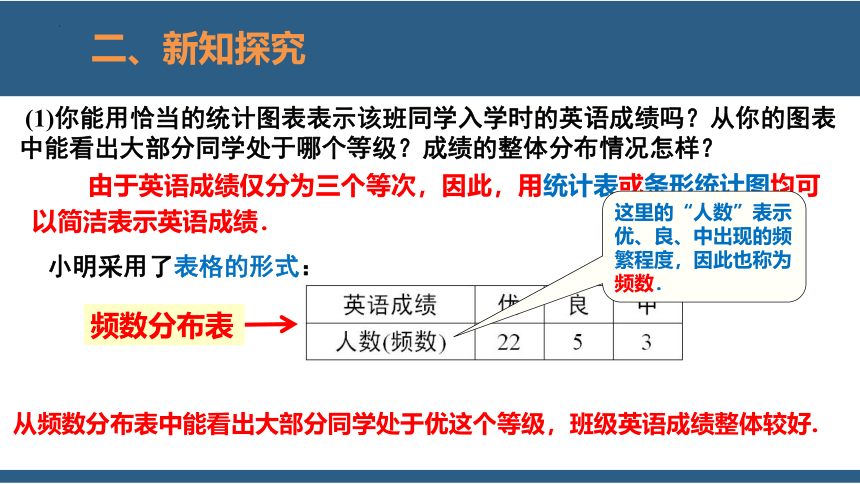
(1)你能用恰当的统计图表表示该班同学入学时的英语成绩吗?从你的图表中能看出大部分同学处于哪个等级?成绩的整体分布情况怎样?
频数分布表
由于英语成绩仅分为三个等次,因此,用统计表或条形统计图均可以简洁表示英语成绩.
小明采用了表格的形式:
从频数分布表中能看出大部分同学处于优这个等级,班级英语成绩整体较好.
这里的“人数”表示优、良、中出现的频繁程度,因此也称为频数.
二、新知探究
条形统计图
小颖采用了条形统计图的形式:
从条形统计图中能看出大部分同学处于优这个等级,班级英语成绩整体较好.
二、新知探究
(2)你能类比上一题,用恰当的统计图表表示该班同学入学时的语文成绩吗?从你的图表中能看出大部分同学的成绩处于哪个分数段?成绩的整体分布情况怎样?
语文成绩/分 68 72 75 78 79 80 81 82 83
人数(频数) 1 1 1 2 1 2 2 2 3
语文成绩/分 85 86 87 88 89 90 91 92 94
人数(频数) 1 4 1 2 1 1 3 1 1
方法一:表格形式(统计表)
二、新知探究
方法二:条形统计图
二、新知探究
我们可以借鉴英语成绩的表示,将语文成绩按10分的距离分段,统计每个分数段的学生数:
思考:小明觉得上面的方法很复杂,你能帮他改进吗?
成绩段 60~70 70~80 80~90 90~100
人数
1
5
18
6
方法三:将数据分组(频数分布表)
60~70表示大于等于60小于70.
从图中你能看出大部分同学处于哪个分数段?成绩的整体分布情况咋样?
从频数分布表中能看出大部分同学处于80~90分.
二、新知探究
方法五 :频数直方图
方法四 :分组后的条形统计图
我们把图①的横轴(水平的轴叫横轴)略作调整,得到图②,像这样的统计图称为频数直方图.
二、新知探究
知识归纳
1.频数直方图是一种特殊的条形统计图;
2.是将统计对象进行分组后的条形统计图。
3.横轴表示各组,纵轴表示各组数据的频数。
4.特点:如果样本中数据较多,数据的差距也比较大时,频数直方图能更清晰、更直观地反映数据的整体状况.
频数直方图:
二、新知探究
做一做:请将前面表格中的数学成绩按10分的距离分段,用频数直方图表示.
解:
成绩/分 60~70 70~80 80~90 90~100
人数(频数) 1 4 14 11
二、新知探究
知识归纳
思考:条形统计图与频数直方图有什么区别和联系?
(1)联系——用途都是可以直观地表示出具体数量.频数直方图是特殊的条形统计图.
(3)绘制的形式不同——条形统计图各条形分开;频数直方图的条形连在一起.
(2)区别——条形统计图是直观地显示出具体数据;频数直方图是表现频数的分布情况.
例1:为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了100名学生进行统计,并绘成如图所示的频数直方图,已知该校共有1000名学生.据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )
A.280 B.240 C.300 D.260
三、典例精析
A
[解析] A 由频数直方图知样本中参加社团活动时间在8~10小时之间的学生数是100-30-24-10-8=28,占28÷100×100%=28%,采用样本估计总体的方法知该校五一期间参加社团活动时间在8~10小时之间的学生数大约是1000×28%=280.故选A.
例2:某市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出频数分布表和频数直方图(不完整)如下:
请结合图表完成下列各题:(1)求表中a的值;
(2)请把频数直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
三、典例精析
解:(1)a=50-4-8-16-10=12.
(2)如图所示.
四、当堂练习
1.在频数分布表中,各小组的频数之和( )
A.小于数据总数 B.等于数据总数
C.大于数据总数 D.不能确定
2.学校为了了解七年级700名学生上学期参加社会实践活动的时间,随机对该年级50名学生进行了调查.根据收集的数据绘制了如图所示的频数直方图,则以下说法正确的是( )
A.绘制该频数直方图时选取的组距为10,分成的组数为5
B.这50人中大多数学生参加社会实践活动的时间是12~14 h
C.这50人中有64%的学生参加社会实践活动的时间不少于10 h
D.可以估计全年级700人中参加社会实践活动时间为6~8 h的学生约为28人
B
D
4.某班级的一次数学考试成绩统计图如图所示,则下列说法错误的是( )
A.得分在70~80分的人数最多
B.该班的总人数为40
C.人数最少的得分段的频数为2
D.得分及格(≥60)的有12人
3.如图所示是某班45名同学爱心捐款额的频数直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )
A.5~10元 B.10~15元
C.15~20元 D.20~25元
四、当堂练习
D
C
6.某校七(1)班有48人,对本班学生展开零花钱的钱数调查,绘制了如图所示的频数直方图,已知从左到右小长方形的高度之比为2∶3∶4∶2∶1,则零花钱在8元以上的共有________人.
5.某校开展捐书活动,七(1)班同学积极参与,现将捐书数量绘制成频数直方图(如图所示),如果捐书数量在3.5~4.5组别的人数占总人数的30%,那么捐书数量在4.5~5.5组别的人数是________人.
四、当堂练习
16
12
7.某校进行信息技术模拟测试,七年级(1)班的最高分为99分,最低分为40分,课代表将全班同学的成绩(得分取整数)进行整理后分为6个小组,制成如图49—2所示不完整的频数直方图,其中在39.5~59.5分的学生人数占全班学生人数的8%,结合频数直方图提供的信息,解答下列问题:
(1)七年级(1)班共有多少名学生?
(2)补全频数直方图;
(3)若80分及80分以上为优秀,则优秀人数占全班人数的百分比是多少?
四、当堂练习
解:(1)(2+2)÷8%=50(名).
(2)69.5~79.5分的学生有50-2-2-8-18-8=12(名),补全频数直方图略.
8.某校为了了解九年级1 000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.解答下列问题:(1)这次抽样调查了________名学生,并补全频数直方图;(2)在扇形统计图中,D组的圆心角是______度.
50
72
四、当堂练习
五、课堂小结
频数直方图
条形统计图与频数直方图的联系和区别
数据的表示(频数直方图)
(3)绘制不同:条形统计图各条形分开,频数直方图的条形连在一起.
(2)区别:条形统计图是直观地显示出具体数据,频数直方图是表现频数的分布情况.
(1)联系:它们都可以直观地表示出具体数量,频数直方图是特殊的条形统计图.
频数直方图是一种特殊的条形统计图,它将统计对象的数据进行了分组画在横轴上,纵轴表示各组数据的频数。如果样本中数据较多,数据的差距也比较大时,频数直方图能更清晰、更直观地反映数据的整体状况.
六、作业布置
习题6.4
北师大版 数学 七年级上册
第2课时
3 数据的表示
第六章 数据的收集与整理
学习目标
1.了解频数分布直方图;(重点)
2.会从频数分布直方图中获得数据信息;(重点)
3.能够根据已知题目画出频数分布直方图.(重、难点)
1.圆代表 , 圆中的各个扇形分别代表总体中的不同部分, 扇形的大小反映 的大小。 这样的统计图叫做扇形统计图。
排球18%
足球25%
乒乓球32%
篮球19%
其他6%
一、导入新课
复习回顾
(1)计算总体数目。
2.扇形统计图的画法的步骤:
(2)计算各部分占总体的百分比。
(3)计算扇形的圆心角。
(4)画图。
(5)标上百分比。
(6)标上图形的名称。
总体
部分占总体百分比
2.在扇形统计图中,每部分占总体的百分比等于该部分所对应的__________________与________的比.
扇形圆心角的度数
360°
一、导入新课
情境导入
A
A
B
C
D
A
B
A
A
C
B
A
A
C
B
C
A
A
B
C
A
A
B
A
C
D
A
A
C
D
B
A
C
D
A
A
A
C
D
A
C
B
A
A
C
C
D
A
A
C
书籍是人类进步的阶梯,同学们在课外最爱读那一类书籍?
文学类(A)、漫画类(B)科普类(C)、历史类(D)
下面是小亮调查的七(1)班50位同学喜欢的书籍,结果如下:
根据上面结果,你能很快说出该班同学最喜欢读那一类书吗?他的数据表示方式是什么?
这些数据没有经过统计、整理,必须把A、B、C、D的个数全部数清,才能比较出哪类书是该班同学最喜欢的.数据越多越不方便,所以小亮的数据表示方式不太好.
一、导入新课
情境导入
你能设计出一个比较好的表示方式吗?可以用如下方式表示:
此种表示方式的优点是什么?
简单明了,一眼可以看出哪个最多、哪个最少.
此种表示方式的优点是什么?
直观,一目了然.不仅可以很快判断出哪个最多,哪个最少,还可比较出差别是否悬殊很大.
还可以采用如右图方式表示数据.
5
10
15
20
25
A
B
C
D
学生人数
书的类别
23
8
13
6
二、新知探究
探究:用频数直方图表示数据
右表是某校七年级(2)班的同学入学信息表:
二、新知探究
(1)你能用恰当的统计图表表示该班同学入学时的英语成绩吗?从你的图表中能看出大部分同学处于哪个等级?成绩的整体分布情况怎样?
频数分布表
由于英语成绩仅分为三个等次,因此,用统计表或条形统计图均可以简洁表示英语成绩.
小明采用了表格的形式:
从频数分布表中能看出大部分同学处于优这个等级,班级英语成绩整体较好.
这里的“人数”表示优、良、中出现的频繁程度,因此也称为频数.
二、新知探究
条形统计图
小颖采用了条形统计图的形式:
从条形统计图中能看出大部分同学处于优这个等级,班级英语成绩整体较好.
二、新知探究
(2)你能类比上一题,用恰当的统计图表表示该班同学入学时的语文成绩吗?从你的图表中能看出大部分同学的成绩处于哪个分数段?成绩的整体分布情况怎样?
语文成绩/分 68 72 75 78 79 80 81 82 83
人数(频数) 1 1 1 2 1 2 2 2 3
语文成绩/分 85 86 87 88 89 90 91 92 94
人数(频数) 1 4 1 2 1 1 3 1 1
方法一:表格形式(统计表)
二、新知探究
方法二:条形统计图
二、新知探究
我们可以借鉴英语成绩的表示,将语文成绩按10分的距离分段,统计每个分数段的学生数:
思考:小明觉得上面的方法很复杂,你能帮他改进吗?
成绩段 60~70 70~80 80~90 90~100
人数
1
5
18
6
方法三:将数据分组(频数分布表)
60~70表示大于等于60小于70.
从图中你能看出大部分同学处于哪个分数段?成绩的整体分布情况咋样?
从频数分布表中能看出大部分同学处于80~90分.
二、新知探究
方法五 :频数直方图
方法四 :分组后的条形统计图
我们把图①的横轴(水平的轴叫横轴)略作调整,得到图②,像这样的统计图称为频数直方图.
二、新知探究
知识归纳
1.频数直方图是一种特殊的条形统计图;
2.是将统计对象进行分组后的条形统计图。
3.横轴表示各组,纵轴表示各组数据的频数。
4.特点:如果样本中数据较多,数据的差距也比较大时,频数直方图能更清晰、更直观地反映数据的整体状况.
频数直方图:
二、新知探究
做一做:请将前面表格中的数学成绩按10分的距离分段,用频数直方图表示.
解:
成绩/分 60~70 70~80 80~90 90~100
人数(频数) 1 4 14 11
二、新知探究
知识归纳
思考:条形统计图与频数直方图有什么区别和联系?
(1)联系——用途都是可以直观地表示出具体数量.频数直方图是特殊的条形统计图.
(3)绘制的形式不同——条形统计图各条形分开;频数直方图的条形连在一起.
(2)区别——条形统计图是直观地显示出具体数据;频数直方图是表现频数的分布情况.
例1:为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了100名学生进行统计,并绘成如图所示的频数直方图,已知该校共有1000名学生.据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )
A.280 B.240 C.300 D.260
三、典例精析
A
[解析] A 由频数直方图知样本中参加社团活动时间在8~10小时之间的学生数是100-30-24-10-8=28,占28÷100×100%=28%,采用样本估计总体的方法知该校五一期间参加社团活动时间在8~10小时之间的学生数大约是1000×28%=280.故选A.
例2:某市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出频数分布表和频数直方图(不完整)如下:
请结合图表完成下列各题:(1)求表中a的值;
(2)请把频数直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
三、典例精析
解:(1)a=50-4-8-16-10=12.
(2)如图所示.
四、当堂练习
1.在频数分布表中,各小组的频数之和( )
A.小于数据总数 B.等于数据总数
C.大于数据总数 D.不能确定
2.学校为了了解七年级700名学生上学期参加社会实践活动的时间,随机对该年级50名学生进行了调查.根据收集的数据绘制了如图所示的频数直方图,则以下说法正确的是( )
A.绘制该频数直方图时选取的组距为10,分成的组数为5
B.这50人中大多数学生参加社会实践活动的时间是12~14 h
C.这50人中有64%的学生参加社会实践活动的时间不少于10 h
D.可以估计全年级700人中参加社会实践活动时间为6~8 h的学生约为28人
B
D
4.某班级的一次数学考试成绩统计图如图所示,则下列说法错误的是( )
A.得分在70~80分的人数最多
B.该班的总人数为40
C.人数最少的得分段的频数为2
D.得分及格(≥60)的有12人
3.如图所示是某班45名同学爱心捐款额的频数直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )
A.5~10元 B.10~15元
C.15~20元 D.20~25元
四、当堂练习
D
C
6.某校七(1)班有48人,对本班学生展开零花钱的钱数调查,绘制了如图所示的频数直方图,已知从左到右小长方形的高度之比为2∶3∶4∶2∶1,则零花钱在8元以上的共有________人.
5.某校开展捐书活动,七(1)班同学积极参与,现将捐书数量绘制成频数直方图(如图所示),如果捐书数量在3.5~4.5组别的人数占总人数的30%,那么捐书数量在4.5~5.5组别的人数是________人.
四、当堂练习
16
12
7.某校进行信息技术模拟测试,七年级(1)班的最高分为99分,最低分为40分,课代表将全班同学的成绩(得分取整数)进行整理后分为6个小组,制成如图49—2所示不完整的频数直方图,其中在39.5~59.5分的学生人数占全班学生人数的8%,结合频数直方图提供的信息,解答下列问题:
(1)七年级(1)班共有多少名学生?
(2)补全频数直方图;
(3)若80分及80分以上为优秀,则优秀人数占全班人数的百分比是多少?
四、当堂练习
解:(1)(2+2)÷8%=50(名).
(2)69.5~79.5分的学生有50-2-2-8-18-8=12(名),补全频数直方图略.
8.某校为了了解九年级1 000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.解答下列问题:(1)这次抽样调查了________名学生,并补全频数直方图;(2)在扇形统计图中,D组的圆心角是______度.
50
72
四、当堂练习
五、课堂小结
频数直方图
条形统计图与频数直方图的联系和区别
数据的表示(频数直方图)
(3)绘制不同:条形统计图各条形分开,频数直方图的条形连在一起.
(2)区别:条形统计图是直观地显示出具体数据,频数直方图是表现频数的分布情况.
(1)联系:它们都可以直观地表示出具体数量,频数直方图是特殊的条形统计图.
频数直方图是一种特殊的条形统计图,它将统计对象的数据进行了分组画在横轴上,纵轴表示各组数据的频数。如果样本中数据较多,数据的差距也比较大时,频数直方图能更清晰、更直观地反映数据的整体状况.
六、作业布置
习题6.4
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
