6.3一次函数的图像(第1课时) 同步课件(共26张PPT)
文档属性
| 名称 | 6.3一次函数的图像(第1课时) 同步课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 00:00:00 | ||
图片预览




文档简介
(共26张PPT)
第6章 · 一次函数
6.3 一次函数的图像(1)
第1课时 一次函数的图像
学习目标
1. 通过生活中的实例感受一次函数的图像,知道一次函数的图像是一条直线;
2. 经历一次函数图像的作图过程,初步了解作函数图像的一般步骤,并会选取适当两个点画一次函数的图像.
知识回顾
函数有3种表示方法.
列表法:
函数表达式法:
图像法:
1.函数有几种表示方法?
把自变量的值和对应的函数值列成表格来表示函数关系的方法叫做列表法.
表示两个变量之间函数关系的式子称为函数表达式.
在平面直角坐标系中,以函数的自变量的值为横坐标、对应的函数值为纵坐标的点所组成的图形叫做这个函数的图像.
2.什么是一次函数?
一般地,形如y=kx+b(k、b 是常数,且k≠0)的函数,叫做一次函数,其中x是自变量,y是x的函数.
一次函数的图像是什么样的图形呢?
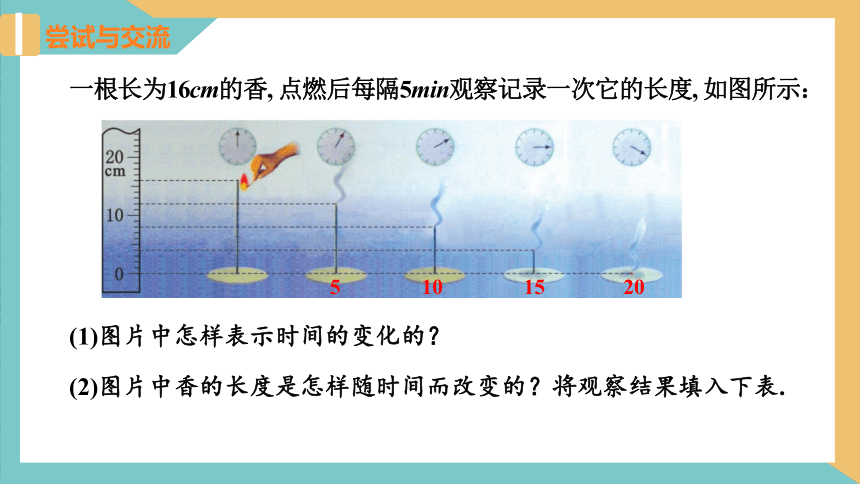
一根长为16cm的香, 点燃后每隔5min观察记录一次它的长度, 如图所示:
尝试与交流
(1)图片中怎样表示时间的变化的?
5
10
15
20
(2)图片中香的长度是怎样随时间而改变的?将观察结果填入下表.
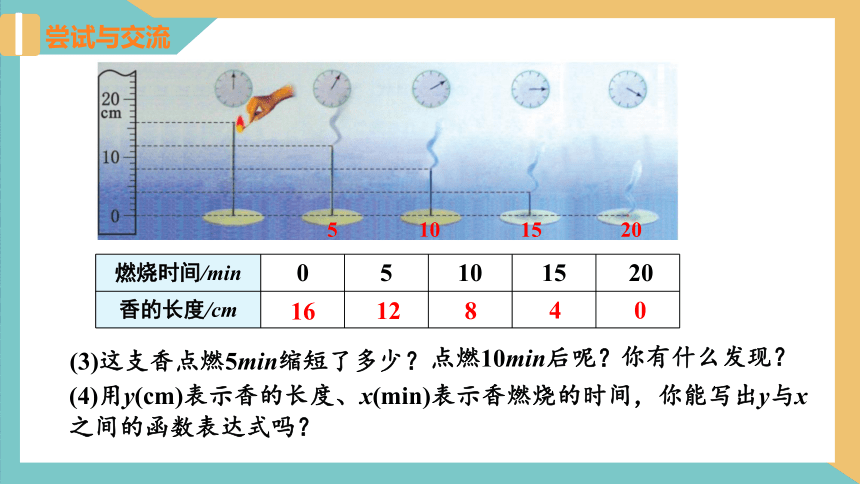
燃烧时间/min 0 5 10 15 20
香的长度/cm
尝试与交流
5
10
15
20
16
12
8
4
0
(3)这支香点燃5min缩短了多少?
点燃10min后呢?
你有什么发现?
(4)用y(cm)表示香的长度、x(min)表示香燃烧的时间,你能写出y与x之间的函数表达式吗?
尝试与交流
5
10
15
20
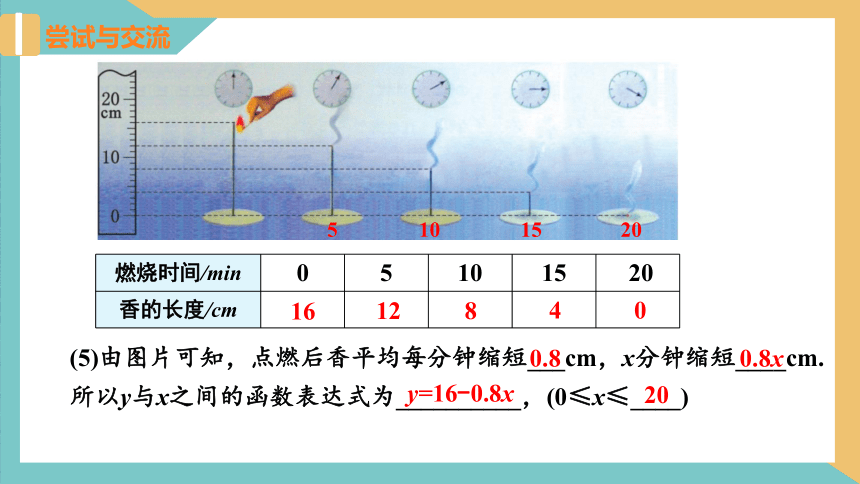
(5)由图片可知,点燃后香平均每分钟缩短___cm,x分钟缩短____cm.所以y与x之间的函数表达式为__________,(0≤x≤____)
0.8
0.8x
y=16-0.8x
20
燃烧时间/min 0 5 10 15 20
香的长度/cm
16
12
8
4
0
尝试与交流
5
10
15
20
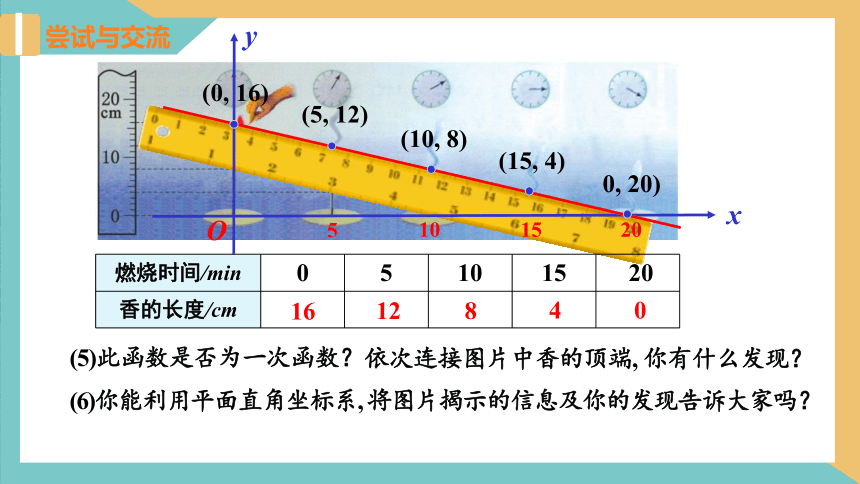
(5)此函数是否为一次函数?
依次连接图片中香的顶端, 你有什么发现?
(6)你能利用平面直角坐标系, 将图片揭示的信息及你的发现告诉大家吗?
(0, 16)
(5, 12)
(10, 8)
(15, 4)
0, 20)
x
y
O
燃烧时间/min 0 5 10 15 20
香的长度/cm
16
12
8
4
0
1
2
y
3
4
5
-2
-3
尝试与交流
按下列步骤,在平面直角坐标系中,画一次函数y=2x+1的图像.
①列表:恰当的选取自变量x的几个值,计算函数y相应的值;
x ··· -2 -1 0 1 2 ···
y ··· ···
-3
-2
1
3
5
4
5
3
2
O
x
1
-1
-2
-1
②描点:以表中各对x、y的值为点的坐标,在平面直角坐标系中描出相应的点;
③连线:顺次连接描出的各点.
y=2x+1
尝试与交流
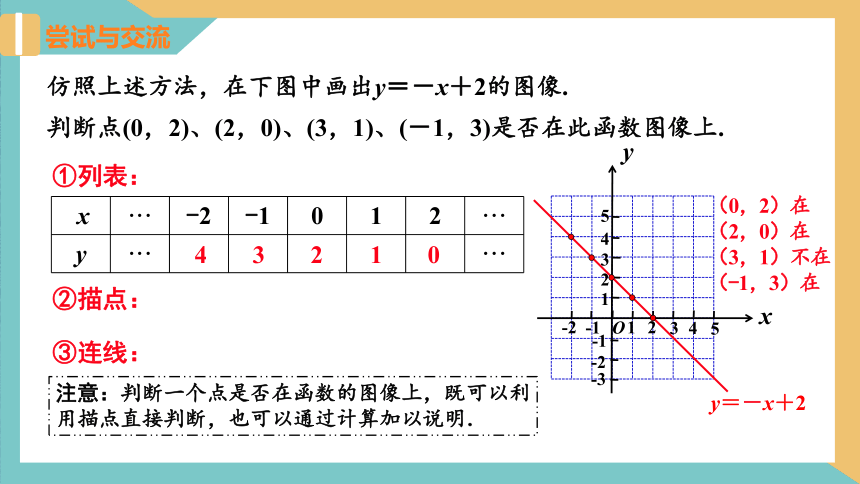
仿照上述方法,在下图中画出y=-x+2的图像.
判断点(0,2)、(2,0)、(3,1)、(-1,3)是否在此函数图像上.
x ··· -2 -1 0 1 2 ···
y ··· ···
4
3
2
1
0
1
2
y
3
4
5
-2
-3
4
5
3
2
O
x
1
-1
-2
-1
y=-x+2
①列表:
②描点:
③连线:
(0,2)在
(2,0)在
(3,1)不在
(-1,3)在
注意:判断一个点是否在函数的图像上,既可以利用描点直接判断,也可以通过计算加以说明.
讨论与交流
思考:1.画一次函数图像的一般步骤是什么?
(1)列表;(2)描点;(3)连线.
先取x的值,再根据函数表达式求出y的值.
2. 在列表时,是先取x的值还是先取y的值?另一个变量的值是如何确定的?连线时要注意什么?
连线时要注意按照顺序用平滑的线连接.
3.一次函数的图像是什么样的图形?
一条直线.
新知归纳
一次函数y=kx+b(k,b都为常数且k≠0)可以用直角坐标系中的一条直线来表示,这条直线也叫做一次函数y=kx+b的图像,以后就称它为:直线 y=kx+b .
思考:画一次函数的图像有没有简捷的方法呢?
取怎样的两点比较方便?
只要确定两个点的位置,这是因为两点确定一条直线.
例题讲解
例1 在直角坐标系中,画一次函数y=-3x+3的图像.
解:把 x=0 代入y=-3x+3,得 y=3.
过点(0,3)、(1,0)画一条直线,这条直线就是函数y=-3x+3的图像.
把 y=0 代入y=-3x+3,得 x=1.
1
2
y
3
4
5
-2
-3
4
5
3
2
O
x
1
-1
-2
-1
y=-3x+3
归纳总结
画一次函数y=kx+b(k≠0)的图像时,只要确定2 个点的位置,
即点(0,___ ),点( ___,0)
b
-
画正比例函数y=kx(k≠0)的图像时,一般确定哪两个点?
一般取(0,0),(1,k)两点画直线.
正比例函数y=kx(k≠0)的图像是经过原点的一条直线.
新知巩固
1. 在同一平面直角坐标系中,画函数y=x+3和y=-4x-5的图像.
点A(2,4)、B(-,-3)分别在哪个图像上?
x 0
y=x+3 0
3
-6
1
2
y
3
4
5
-2
-3
-1
-4
-5
4
5
3
2
O
x
1
-1
-2
-3
-4
-5
-6
y=x+3
x 0
y=-4x-5 0
-5
-
y=-4x-5
新知巩固
x 0
y=2x+1 0
x 0
y=2x-1 0
2. 在同一平面直角坐标系中,画函数y=2x+1、y=2x-1和y=2x的图像.
1
-
1
y
2
-1
2
1
O
x
-1
y=2x+1
-1
y=2x-1
x 0 1
y=2x
0
2
y=2x
这三条直线的位置有什么关系?
这三条直线互相平行.
3. 如图,直线l是一次函数y=kx+b的图像. 求:
(1)这个函数的表达式;
(2)当x=4时,y的值.
1
2
y
3
4
5
-2
-3
4
5
3
2
O
x
1
-1
-2
-1
l
解:(1)一次函数y=kx+b的图像经过(-2,0),(2,2)
两点,依题意,得
解得
所以这个函数的表达式为y=x+1.
(2)当x=4时,y=×4+1=3.
新知巩固
课堂小结
一次函数
的图像
画法
描点法
列表描点连线
图像
一条直线
1. 若点P(2,1)在过原点的一条直线上,则这条直线所对应的函数表达式为( )A.y=-2x B.y=x C.y=2x-1 D.y=1-2x
当堂检测
B
2. 下列两点在函数y=-2x+3图像上的是 ( )
A.原点和点(1,1) B.点(1,1)和点(2,3)
C.点(0,3)和点(1,1) D.点(0,3)和点(2,3)..
C
当堂检测
3.在平面直角坐标系中,一次函数y=x-1的图像是 ( )
B
4. 若点P(a,b)是正比例函数y=-x图像上任意一点,则下列等式一定成立的是( )A.2a+3b=0 B.2a-3b=0 C.3a+2b=0 D.3a-2b=0
A
当堂检测
5. (1)正比例函数y=2x的图像过点(0,___)和点(1,___ );
(2)一次函数y=-x+3的图像过点(0,___)和点(___,0).
0
2
3
3
6. 直线y=2x+3与直线y=2x-1的位置关系是________.
平行
7. 若直线y=kx-3经过点(1,-2)和点(0,b),则k-b的值是____.
4
当堂检测
8. 如图,点A(-3,4)在一次函数y=-3x+b的图像上,该一次函数的图像与y轴的交点为B,那么△AOB的面积为________.
当堂检测
9. 若三点(1,4),(2,7),(a,10)在同一直线上,求a的值.
解:设经过(1,4),(2,7)两点的直线表达式为y=kx+b,∴
∴∴y=3x+1,
将点(a,10)代入表达式,得3a+1=10,
∴a=3.
思维提升
1. 已知一次函数y=kx-2k+1(k≠0),回答下列问题:
(1)若此函数的图像过原点,求k的值;
解:∵一次函数y=kx-2k+1的图像过原点,∴-2k+1=0,解得k=.
(2)无论k取何值, 该函数图像总经过一个定点, 请你求出这个定点的坐标.
解:∵y=kx-2k+1=k(x-2)+1,∴(x-2)k=y-1.∵无论k取何值,该函数图像总经过一个定点,即k有无数个解,∴x-2=0,y-1=0,解得x=2,y=1,∴这个定点的坐标为(2,1).
新知巩固
2.已知一次函数y=x+2与y=-2x+3,
(1)在同一直角坐标系中画出上述函数的图像,并求出它们与坐标轴交点的坐标 .
1
2
y
3
4
5
-2
-3
-1
-4
-5
4
5
3
2
O
x
1
-1
-2
-3
-4
-5
-6
y=x+2
y=-2x+3
解:(1)y=x+2与x轴交点坐标为(-2,0),与y轴交点坐标为(0,2);
y=-2x+3与x轴交点坐标为(,0),与y轴交点坐标为(0,3).
新知巩固
2.已知一次函数y=x+2与y=-2x+3 ,
(2)求这两条直线的交点坐标 .
解:(2)
∴∴交点坐标为(,)
1
2
y
3
4
5
-2
-3
-1
-4
-5
4
5
3
2
O
x
1
-1
-2
-3
-4
-5
-6
y=x+2
y=-2x+3
新知巩固
2.已知一次函数y=x+2与y=-2x+3 ,
(3)求这两条直线与坐标轴所围成的图形面积.
1
2
y
3
4
5
-2
-3
-1
-4
-5
4
5
3
2
O
x
1
-1
-2
-3
-4
-5
-6
y=x+2
y=-2x+3
(,)
解:(3)S=×[]×=
第6章 · 一次函数
6.3 一次函数的图像(1)
第1课时 一次函数的图像
学习目标
1. 通过生活中的实例感受一次函数的图像,知道一次函数的图像是一条直线;
2. 经历一次函数图像的作图过程,初步了解作函数图像的一般步骤,并会选取适当两个点画一次函数的图像.
知识回顾
函数有3种表示方法.
列表法:
函数表达式法:
图像法:
1.函数有几种表示方法?
把自变量的值和对应的函数值列成表格来表示函数关系的方法叫做列表法.
表示两个变量之间函数关系的式子称为函数表达式.
在平面直角坐标系中,以函数的自变量的值为横坐标、对应的函数值为纵坐标的点所组成的图形叫做这个函数的图像.
2.什么是一次函数?
一般地,形如y=kx+b(k、b 是常数,且k≠0)的函数,叫做一次函数,其中x是自变量,y是x的函数.
一次函数的图像是什么样的图形呢?
一根长为16cm的香, 点燃后每隔5min观察记录一次它的长度, 如图所示:
尝试与交流
(1)图片中怎样表示时间的变化的?
5
10
15
20
(2)图片中香的长度是怎样随时间而改变的?将观察结果填入下表.
燃烧时间/min 0 5 10 15 20
香的长度/cm
尝试与交流
5
10
15
20
16
12
8
4
0
(3)这支香点燃5min缩短了多少?
点燃10min后呢?
你有什么发现?
(4)用y(cm)表示香的长度、x(min)表示香燃烧的时间,你能写出y与x之间的函数表达式吗?
尝试与交流
5
10
15
20
(5)由图片可知,点燃后香平均每分钟缩短___cm,x分钟缩短____cm.所以y与x之间的函数表达式为__________,(0≤x≤____)
0.8
0.8x
y=16-0.8x
20
燃烧时间/min 0 5 10 15 20
香的长度/cm
16
12
8
4
0
尝试与交流
5
10
15
20
(5)此函数是否为一次函数?
依次连接图片中香的顶端, 你有什么发现?
(6)你能利用平面直角坐标系, 将图片揭示的信息及你的发现告诉大家吗?
(0, 16)
(5, 12)
(10, 8)
(15, 4)
0, 20)
x
y
O
燃烧时间/min 0 5 10 15 20
香的长度/cm
16
12
8
4
0
1
2
y
3
4
5
-2
-3
尝试与交流
按下列步骤,在平面直角坐标系中,画一次函数y=2x+1的图像.
①列表:恰当的选取自变量x的几个值,计算函数y相应的值;
x ··· -2 -1 0 1 2 ···
y ··· ···
-3
-2
1
3
5
4
5
3
2
O
x
1
-1
-2
-1
②描点:以表中各对x、y的值为点的坐标,在平面直角坐标系中描出相应的点;
③连线:顺次连接描出的各点.
y=2x+1
尝试与交流
仿照上述方法,在下图中画出y=-x+2的图像.
判断点(0,2)、(2,0)、(3,1)、(-1,3)是否在此函数图像上.
x ··· -2 -1 0 1 2 ···
y ··· ···
4
3
2
1
0
1
2
y
3
4
5
-2
-3
4
5
3
2
O
x
1
-1
-2
-1
y=-x+2
①列表:
②描点:
③连线:
(0,2)在
(2,0)在
(3,1)不在
(-1,3)在
注意:判断一个点是否在函数的图像上,既可以利用描点直接判断,也可以通过计算加以说明.
讨论与交流
思考:1.画一次函数图像的一般步骤是什么?
(1)列表;(2)描点;(3)连线.
先取x的值,再根据函数表达式求出y的值.
2. 在列表时,是先取x的值还是先取y的值?另一个变量的值是如何确定的?连线时要注意什么?
连线时要注意按照顺序用平滑的线连接.
3.一次函数的图像是什么样的图形?
一条直线.
新知归纳
一次函数y=kx+b(k,b都为常数且k≠0)可以用直角坐标系中的一条直线来表示,这条直线也叫做一次函数y=kx+b的图像,以后就称它为:直线 y=kx+b .
思考:画一次函数的图像有没有简捷的方法呢?
取怎样的两点比较方便?
只要确定两个点的位置,这是因为两点确定一条直线.
例题讲解
例1 在直角坐标系中,画一次函数y=-3x+3的图像.
解:把 x=0 代入y=-3x+3,得 y=3.
过点(0,3)、(1,0)画一条直线,这条直线就是函数y=-3x+3的图像.
把 y=0 代入y=-3x+3,得 x=1.
1
2
y
3
4
5
-2
-3
4
5
3
2
O
x
1
-1
-2
-1
y=-3x+3
归纳总结
画一次函数y=kx+b(k≠0)的图像时,只要确定2 个点的位置,
即点(0,___ ),点( ___,0)
b
-
画正比例函数y=kx(k≠0)的图像时,一般确定哪两个点?
一般取(0,0),(1,k)两点画直线.
正比例函数y=kx(k≠0)的图像是经过原点的一条直线.
新知巩固
1. 在同一平面直角坐标系中,画函数y=x+3和y=-4x-5的图像.
点A(2,4)、B(-,-3)分别在哪个图像上?
x 0
y=x+3 0
3
-6
1
2
y
3
4
5
-2
-3
-1
-4
-5
4
5
3
2
O
x
1
-1
-2
-3
-4
-5
-6
y=x+3
x 0
y=-4x-5 0
-5
-
y=-4x-5
新知巩固
x 0
y=2x+1 0
x 0
y=2x-1 0
2. 在同一平面直角坐标系中,画函数y=2x+1、y=2x-1和y=2x的图像.
1
-
1
y
2
-1
2
1
O
x
-1
y=2x+1
-1
y=2x-1
x 0 1
y=2x
0
2
y=2x
这三条直线的位置有什么关系?
这三条直线互相平行.
3. 如图,直线l是一次函数y=kx+b的图像. 求:
(1)这个函数的表达式;
(2)当x=4时,y的值.
1
2
y
3
4
5
-2
-3
4
5
3
2
O
x
1
-1
-2
-1
l
解:(1)一次函数y=kx+b的图像经过(-2,0),(2,2)
两点,依题意,得
解得
所以这个函数的表达式为y=x+1.
(2)当x=4时,y=×4+1=3.
新知巩固
课堂小结
一次函数
的图像
画法
描点法
列表描点连线
图像
一条直线
1. 若点P(2,1)在过原点的一条直线上,则这条直线所对应的函数表达式为( )A.y=-2x B.y=x C.y=2x-1 D.y=1-2x
当堂检测
B
2. 下列两点在函数y=-2x+3图像上的是 ( )
A.原点和点(1,1) B.点(1,1)和点(2,3)
C.点(0,3)和点(1,1) D.点(0,3)和点(2,3)..
C
当堂检测
3.在平面直角坐标系中,一次函数y=x-1的图像是 ( )
B
4. 若点P(a,b)是正比例函数y=-x图像上任意一点,则下列等式一定成立的是( )A.2a+3b=0 B.2a-3b=0 C.3a+2b=0 D.3a-2b=0
A
当堂检测
5. (1)正比例函数y=2x的图像过点(0,___)和点(1,___ );
(2)一次函数y=-x+3的图像过点(0,___)和点(___,0).
0
2
3
3
6. 直线y=2x+3与直线y=2x-1的位置关系是________.
平行
7. 若直线y=kx-3经过点(1,-2)和点(0,b),则k-b的值是____.
4
当堂检测
8. 如图,点A(-3,4)在一次函数y=-3x+b的图像上,该一次函数的图像与y轴的交点为B,那么△AOB的面积为________.
当堂检测
9. 若三点(1,4),(2,7),(a,10)在同一直线上,求a的值.
解:设经过(1,4),(2,7)两点的直线表达式为y=kx+b,∴
∴∴y=3x+1,
将点(a,10)代入表达式,得3a+1=10,
∴a=3.
思维提升
1. 已知一次函数y=kx-2k+1(k≠0),回答下列问题:
(1)若此函数的图像过原点,求k的值;
解:∵一次函数y=kx-2k+1的图像过原点,∴-2k+1=0,解得k=.
(2)无论k取何值, 该函数图像总经过一个定点, 请你求出这个定点的坐标.
解:∵y=kx-2k+1=k(x-2)+1,∴(x-2)k=y-1.∵无论k取何值,该函数图像总经过一个定点,即k有无数个解,∴x-2=0,y-1=0,解得x=2,y=1,∴这个定点的坐标为(2,1).
新知巩固
2.已知一次函数y=x+2与y=-2x+3,
(1)在同一直角坐标系中画出上述函数的图像,并求出它们与坐标轴交点的坐标 .
1
2
y
3
4
5
-2
-3
-1
-4
-5
4
5
3
2
O
x
1
-1
-2
-3
-4
-5
-6
y=x+2
y=-2x+3
解:(1)y=x+2与x轴交点坐标为(-2,0),与y轴交点坐标为(0,2);
y=-2x+3与x轴交点坐标为(,0),与y轴交点坐标为(0,3).
新知巩固
2.已知一次函数y=x+2与y=-2x+3 ,
(2)求这两条直线的交点坐标 .
解:(2)
∴∴交点坐标为(,)
1
2
y
3
4
5
-2
-3
-1
-4
-5
4
5
3
2
O
x
1
-1
-2
-3
-4
-5
-6
y=x+2
y=-2x+3
新知巩固
2.已知一次函数y=x+2与y=-2x+3 ,
(3)求这两条直线与坐标轴所围成的图形面积.
1
2
y
3
4
5
-2
-3
-1
-4
-5
4
5
3
2
O
x
1
-1
-2
-3
-4
-5
-6
y=x+2
y=-2x+3
(,)
解:(3)S=×[]×=
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
