6.3 图形的相似 同步课件

(共25张PPT)
6.3 图形的相似
第6章 图形的相似
教学目标
01
了解相似形的概念，会判断两个图形是否为相似形
02
理解相似多边形、相似比的概念，能快速确定相似多边形的对应边和对应角
相似形
Q1-1：在晴朗的中午，树荫下出现的光斑是什么形状？和谁的形状是一致的？
圆形，与太阳的形状一致
01
情境引入Part1
Q1-2：如图所示的“小孔成像”实验中，光屏上呈现了怎样的像，像的形状与原火焰形状相同吗？
倒立、放大的实像，形状相同
01
情境引入Part1
Q2：下列各组图形有什么共同特征？
形状相同，前5组大小不等，第6组大小相等
01
情境引入Part2
相似形
02
知识精讲
形状相同的图形，叫做相似形。
注意：
(1)判断相似形，只需看两个图形的形状是否相同，与位置、大小无关；
(2)形状相同、大小相等的两个图形全等，全等图形是特殊的相似形。
知识精讲
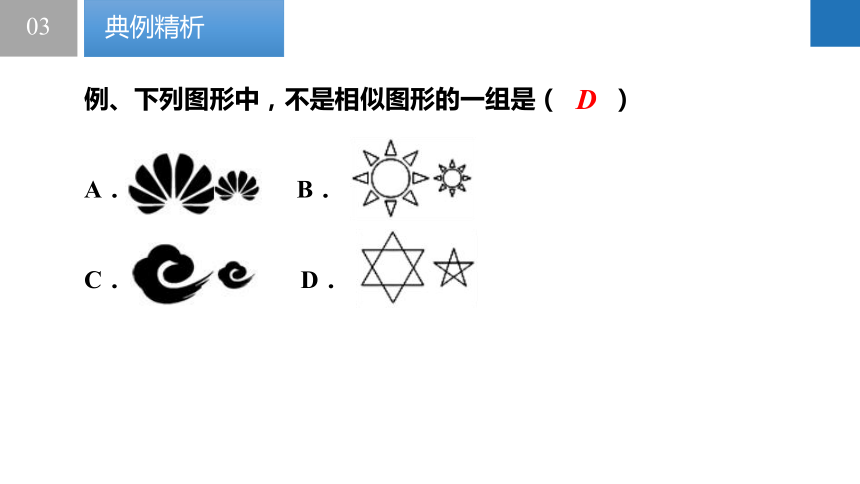
例、下列图形中，不是相似图形的一组是（　　）
A． B．
C． D．
D
03
典例精析
相似多边形
那么，两个多边形究竟要具有怎样的特征才能说它们“形状相同”，称为相似多边形呢？我们借助于几组图来分析~
两个正三角形的各角分别相等，各边成比例
Q1：图(1)中的两个正三角形的边和角分别有怎样的数量关系
C
A’
C’
A
B
B’
图(1)
01
情境引入
通过度量、计算发现：两个三角形的各角相等，各边成比例
C
A’
C’
A
B
B’
图(2)
01
情境引入
Q2：图(2)中的两个三角形的边和角分别有怎样的数量关系
【总结】
∠A=∠A’，∠B=∠B’，∠C=∠C’，==，
△ABC与△A’B’C’相似
两个正方形的各角分别相等，各边成比例
Q3：图(3)中的两个正方形的边和角分别有怎样的数量关系
C
A’
C’
A
B
图(3)
D
B’
D’
01
情境引入
Q4：图(4)中的两个四边形的边和角分别有怎样的数量关系
C
A’
C’
A
B
图(4)
D
B’
D’
通过度量、计算发现：两个四边形的各角相等，各边成比例
01
情境引入
【总结】
∠A=∠A’，∠B=∠B’，∠C=∠C’，∠D=∠D’，===，
四边形ABCD与四边形A’B’C’D’相似
相似多边形
02
知识精讲
像这样，各角分别相等、各边成比例的两个多边形，它们的形状相同，称为相似多边形。
记法与读法：
(1)△ABC与△A’B’C’相似，记作“△ABC∽△A’B’C’”，读作“△ABC相似于△A’B’C’”；
(2)四边形ABCD与四边形A’B’C’D’相似，记作“四边形ABCD∽四边形A’B’C’D’”，读作“四边形ABCD相似于四边形△A’B’C’D’”。
相似比
02
知识精讲
相似多边形的对应角相等，对应边成比例，相似多边形的对应边的比叫做相似比。
C
A’
C’
A
B
图(3)
D
B’
D’
BC=4.5cm
B’C’=3cm
eg：图(3)中的两个正方形的相似比为________。
3:2
议一议1-1：图(5)中的两个矩形是相似多边形吗？为什么？
C
A’
C’
A
B
图(5)
D
B’
D’
不是，两个矩形的各角分别相等，但各边不成比例
02
知识精讲
D’
C
A’
C’
A
B
图(6)
D
B’
02
知识精讲
议一议1-2：图(6)中的两个菱形是相似多边形吗？为什么？
不是，两个菱形的各边成比例，但各角不分别相等
【总结】两个相似多边形必须满足：
①对应角相等；②对应边成比例。（二者缺一不可）
议一议2：△ABC与△A’B’C’相似，可以记作△ABC∽△A’C’B’吗？
不可以，写相似时，字母必须一一对应
02
知识精讲
C
A’
C’
A
B
B’
图(1)
C
A’
C’
A
B
B’
图(2)
知识精讲
例1-1、下列各组图形一定相似的是（　　）
A．有一内角是45°的两个等腰三角形
B．两个等腰三角形
C．两个矩形
D．两个等边三角形
D
【分析】
易错选项A的反例：
顶角45°的等腰三角形与底角45°的等腰三角形不相似。
03
典例精析
知识精讲
例1-2、下列说法正确的是（　　）
A．对应边都成比例的多边形相似
B．对应角都相等的多边形相似
C．边数相同的正多边形不相似
D．两个圆一定相似
【分析】两个相似多边形必须满足：①对应角相等；②对应边成比例，故选项A和B错误；
边数相同的正多边形，形状相同，是相似正多边，故选项C错误。
03
典例精析
D
知识精讲
例2-1、如图所示，若△ABE∽△DCE，分别写出相似图形中的对应角与对应边。
【分析】
对应角：∠A与∠D，∠B与∠C，∠DEC与∠AEB；
对应边：AB与DC，AE与DE，BE与CE。
字母必须要对应
03
典例精析
例2-2、若△ABC的每条边长增加各自的10%得△A′B′C′，则∠B′的度数与其对应角∠B的度数相比（　　）
A．增加了10% B．减少了10%
C．增加了(1+10%) D．没有改变
【分析】∵△ABC的每条边长增加各自的10%得△A′B′C′，
∴△ABC与△A′B′C′的三边对应成比例，
∴△ABC∽△A′B′C′，
∴∠B=∠B′。
03
典例精析
D
知识精讲
例2-3、四边形ABCD和四边形A'B'C'D'是相似图形，点A、B、C、D分别与A'、B'、C'、D'对应，已知BC=3，CD=2.4，B'C′=2，那么C′D'的长是__________。
1.6
【分析】
∵四边形ABCD∽四边形A'B'C'D'，
∴CD:C′D′=BC:B′C′，
∵BC=3，CD=2.4，B'C′=2，
∴C′D′=1.6。
03
典例精析
知识精讲
例3、利用复印机的缩放功能，将原图中边长为5cm的一个正六边形放大成边长为20cm的正六边形，则放大前后的两个正六边形的周长比为__________，面积比为__________。
1:4
1:16
【总结】
若两个相似多边形的对应边之比为m:n，
则两个相似多边形的周长之比为m:n，面积之比为m2:n2。
03
典例精析
课后总结
形状相同的图形，叫做相似形。
注意：
(1)判断相似形，只需看两个图形的形状是否相同，与位置、大小无关；
(2)形状相同、大小相等的两个图形全等，全等图形是特殊的相似形。
像这样，各角分别相等、各边成比例的两个多边形，它们的形状相同，称为相似多边形。
相似多边形的对应角相等，对应边成比例，相似多边形的对应边的比叫做相似比。
若两个相似多边形的对应边之比为m:n，则两个相似多边形的周长之比为m:n，面积之比为m2:n2。