19.9勾股定理(第2课时) 课件(共17张PPT)
文档属性
| 名称 | 19.9勾股定理(第2课时) 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 13:31:22 | ||
图片预览





文档简介
(共17张PPT)
沪教版八年级上册
第 19 章 几何证明
19.9勾股定理(第2课时)
学习目标
1.能用勾股定理解决基本的有关证明和计算问题;
2.通过实际问题的解决增强数学的学习兴趣
谈谈你所见过的勾股定理在生活中的应用:
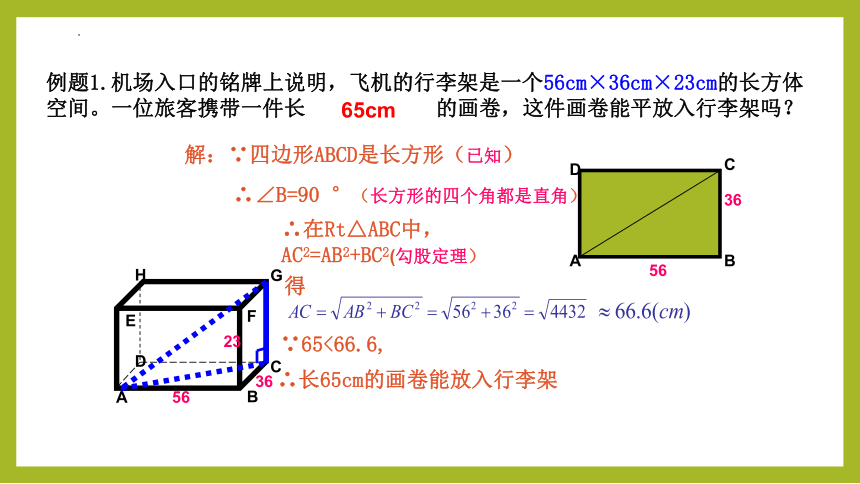
例题1.机场入口的铭牌上说明,飞机的行李架是一个56cm×36cm×23cm的长方体空间。一位旅客携带一件长 的画卷,这件画卷能平放入行李架吗?
36
56
23
A
C
E
B
D
F
G
H
56
36
A
B
C
D
解:∵四边形ABCD是长方形(已知)
∴∠B=90 °(长方形的四个角都是直角)
∴在Rt△ABC中,
AC2=AB2+BC2(勾股定理)
得
∵65<66.6,
∴长65cm的画卷能放入行李架
65cm
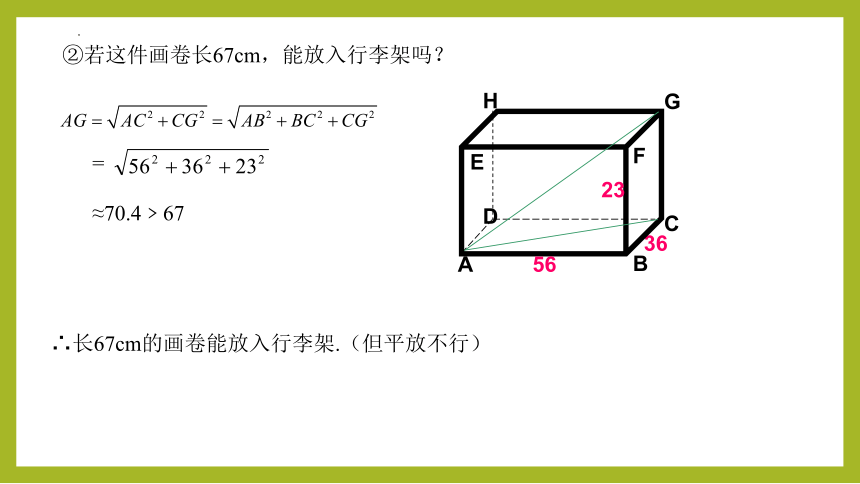
②若这件画卷长67cm,能放入行李架吗?
36
56
23
A
C
E
B
D
F
G
H
=
≈70.4﹥67
∴长67cm的画卷能放入行李架.(但平放不行)
《九章算术》专设勾股章来研究勾股问题,共24个问题.按性质可分为三组,其中第一组的14个问题可以直接利用勾股定理来解决.很多是具有历史地位的世界著名算题.
例题2.《九章算术》勾股章第6题 :
引葭(jiā)赴岸
“今有池方一丈,葭生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.”
现在有一个贮满水的正方形池子,池子的中央长着一株芦苇,水池的边长为10尺,芦苇露出水面1尺。若将芦苇拉到岸边,刚好能达到水池岸与水面的交接线的中点上。请求出水深与芦苇的长各有多少尺?
A
B
C
D
x
x+1
10尺
1尺
(葭:芦苇)
下图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,
旗杆有多高呢?
你能想个办法吗 请你与同伴交流设计方案
小明发现旗杆上的绳子垂到地面还多1米,当他们把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他们把旗杆的高度和绳子的长度计算出来吗?
A
B
C
5
x
x+1
例题3.校园里有一块三角形空地,现准备在这块空地上种植草皮以美化环境,已经测量出它的三边长分别是13、14、15米,若这种草皮每平方米售价120元,则购买这种草皮至少需要支出多少?
15
13
14
A
B
C
D
x
14-x
答:购买这种草皮至少需要支出10080元.
例4:分别作长为
的线段
1
B6
1
B5
1
B4
1
B3
1
B2
1
1
A
B1
C
已知长度为 (n是大于1的整数)的线段,你能作出长度为 的线段吗?
课本练习
【解答】∠ACB =90°,∠A、 ∠ B、 ∠ C所对的边长分别为a、b、c.
2.如图,已知∠A=∠B=∠C=90°,AB=7,AE=6,CD=3,DE=5,求多边形ABCDE的面积
延长CD交AE的延长线于点FF,如图,∵∠A= ∠ B = ∠ C=90°·
∴四边形ABCF是矩形
∠DFE=90°
∴CF =AB =7.AF = BC
∴DF=CF-CD=7-3=4,
1.(2021·上海虹口·八年级期末)直角三角形的两条直角边分别为5和12,那么这个三角形的斜边上的中线长为( )
A.6 B.6.5 C.10 D.13
故选:B.
【点睛】本题主要考查勾股定理及直角三角形斜边中线定理,熟练掌握勾股定理及直角三角形斜边中线定理是解题的关键.
随堂检测
2.甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6 km/h的速度向正东行走,1小时后乙出发,他以5 km/h的速度向正走.上午10:00,甲、乙两人相距多远?
分析:如图已知A是甲、乙的出发点,10:00甲到达B点,乙到达C点.则:
AB=2×6=12(km)
AC=1×5=5(km)
在Rt△ABC中AB +AC =144+25=169
∴BC=13(km)
3.在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
设水池的水深AC为x尺,则这根芦苇长为AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺
由勾股定理得:BC2+AC2=AB2
即 52+x2=(x+1)2
25+x2= x2+2x+1,
2x=24,
∴ x =12, x+1=13 .
答:水池的水深12尺,这根芦苇长13尺.
解:
沪教版八年级上册
第 19 章 几何证明
19.9勾股定理(第2课时)
学习目标
1.能用勾股定理解决基本的有关证明和计算问题;
2.通过实际问题的解决增强数学的学习兴趣
谈谈你所见过的勾股定理在生活中的应用:
例题1.机场入口的铭牌上说明,飞机的行李架是一个56cm×36cm×23cm的长方体空间。一位旅客携带一件长 的画卷,这件画卷能平放入行李架吗?
36
56
23
A
C
E
B
D
F
G
H
56
36
A
B
C
D
解:∵四边形ABCD是长方形(已知)
∴∠B=90 °(长方形的四个角都是直角)
∴在Rt△ABC中,
AC2=AB2+BC2(勾股定理)
得
∵65<66.6,
∴长65cm的画卷能放入行李架
65cm
②若这件画卷长67cm,能放入行李架吗?
36
56
23
A
C
E
B
D
F
G
H
=
≈70.4﹥67
∴长67cm的画卷能放入行李架.(但平放不行)
《九章算术》专设勾股章来研究勾股问题,共24个问题.按性质可分为三组,其中第一组的14个问题可以直接利用勾股定理来解决.很多是具有历史地位的世界著名算题.
例题2.《九章算术》勾股章第6题 :
引葭(jiā)赴岸
“今有池方一丈,葭生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.”
现在有一个贮满水的正方形池子,池子的中央长着一株芦苇,水池的边长为10尺,芦苇露出水面1尺。若将芦苇拉到岸边,刚好能达到水池岸与水面的交接线的中点上。请求出水深与芦苇的长各有多少尺?
A
B
C
D
x
x+1
10尺
1尺
(葭:芦苇)
下图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,
旗杆有多高呢?
你能想个办法吗 请你与同伴交流设计方案
小明发现旗杆上的绳子垂到地面还多1米,当他们把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他们把旗杆的高度和绳子的长度计算出来吗?
A
B
C
5
x
x+1
例题3.校园里有一块三角形空地,现准备在这块空地上种植草皮以美化环境,已经测量出它的三边长分别是13、14、15米,若这种草皮每平方米售价120元,则购买这种草皮至少需要支出多少?
15
13
14
A
B
C
D
x
14-x
答:购买这种草皮至少需要支出10080元.
例4:分别作长为
的线段
1
B6
1
B5
1
B4
1
B3
1
B2
1
1
A
B1
C
已知长度为 (n是大于1的整数)的线段,你能作出长度为 的线段吗?
课本练习
【解答】∠ACB =90°,∠A、 ∠ B、 ∠ C所对的边长分别为a、b、c.
2.如图,已知∠A=∠B=∠C=90°,AB=7,AE=6,CD=3,DE=5,求多边形ABCDE的面积
延长CD交AE的延长线于点FF,如图,∵∠A= ∠ B = ∠ C=90°·
∴四边形ABCF是矩形
∠DFE=90°
∴CF =AB =7.AF = BC
∴DF=CF-CD=7-3=4,
1.(2021·上海虹口·八年级期末)直角三角形的两条直角边分别为5和12,那么这个三角形的斜边上的中线长为( )
A.6 B.6.5 C.10 D.13
故选:B.
【点睛】本题主要考查勾股定理及直角三角形斜边中线定理,熟练掌握勾股定理及直角三角形斜边中线定理是解题的关键.
随堂检测
2.甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6 km/h的速度向正东行走,1小时后乙出发,他以5 km/h的速度向正走.上午10:00,甲、乙两人相距多远?
分析:如图已知A是甲、乙的出发点,10:00甲到达B点,乙到达C点.则:
AB=2×6=12(km)
AC=1×5=5(km)
在Rt△ABC中AB +AC =144+25=169
∴BC=13(km)
3.在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
设水池的水深AC为x尺,则这根芦苇长为AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺
由勾股定理得:BC2+AC2=AB2
即 52+x2=(x+1)2
25+x2= x2+2x+1,
2x=24,
∴ x =12, x+1=13 .
答:水池的水深12尺,这根芦苇长13尺.
解:
