19.9勾股定理(第3课时)(教学课件)-2023-2024学年八年级数学上册同步精品课堂(沪教版)
文档属性
| 名称 | 19.9勾股定理(第3课时)(教学课件)-2023-2024学年八年级数学上册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
沪教版八年级上册
第 19 章 几何证明
19.9勾股定理(第3课时)
1.掌握勾股定理逆定理的概念并理解互逆命题、定
理的概念、关系及勾股数.(重点)
2.能证明勾股定理的逆定理,能利用勾股定理的逆
定理判断一个三角形是直角三角形.(难点)
学习目标
a
b
c
C
B
A
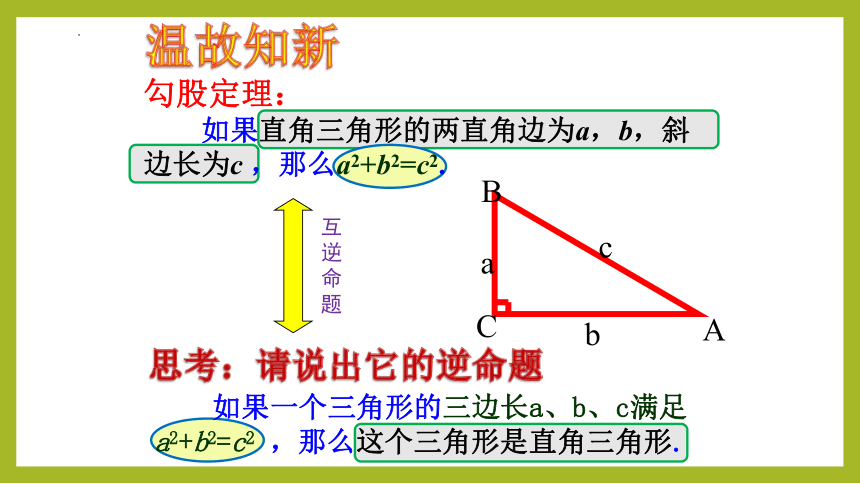
勾股定理:
如果直角三角形的两直角边为a,b,斜边长为c ,那么a2+b2=c2.
如果一个三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形.
互逆命题
新课导入
情景引入
同学们你们知道古埃及人用什么方法得到直角的吗
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(13)
(12)
(11)
(10)
(9)
打13个等距的结,把一根绳子分成等长的12段,然后以3段,4段,5段的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
新课导入
思考:从前面我们知道古埃及人认为一个三角形三边长分别为3,4,5,那么这个三角形为直角三角形.按照这种做法真能得到一个直角三角形吗
大禹治水
相传,我国古代的大禹在治水时也用了类似的方法确定直角.
那么,当
①
时,
三角形ABC是直角三角形吗
当然是!
那么,当
三角形ABC是直角三角形吗
②
时,
想一想,猜一猜!
提出问题
C
A
B
a
b
c
分析问题
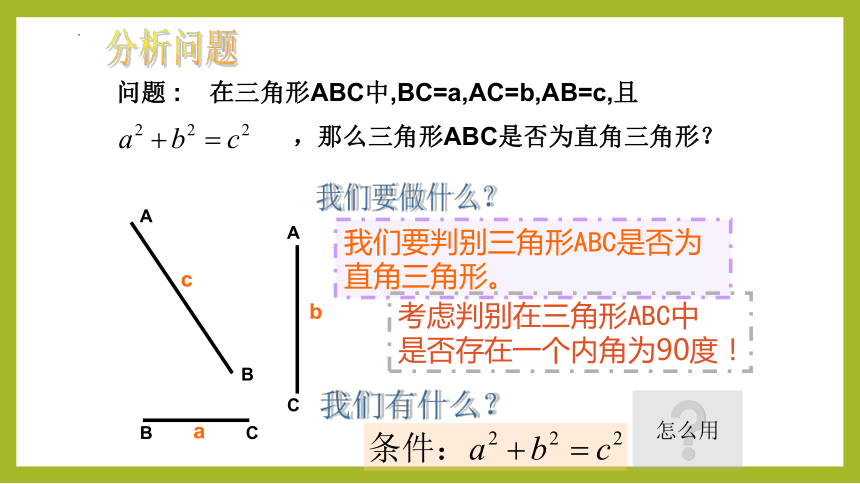
问题 : 在三角形ABC中,BC=a,AC=b,AB=c,且
,那么三角形ABC是否为直角三角形?
B
C
A
B
A
C
a
b
c
我们要判别三角形ABC是否为直角三角形。
我们要做什么?
我们有什么?
考虑判别在三角形ABC中
是否存在一个内角为90度!
怎么用
分析问题
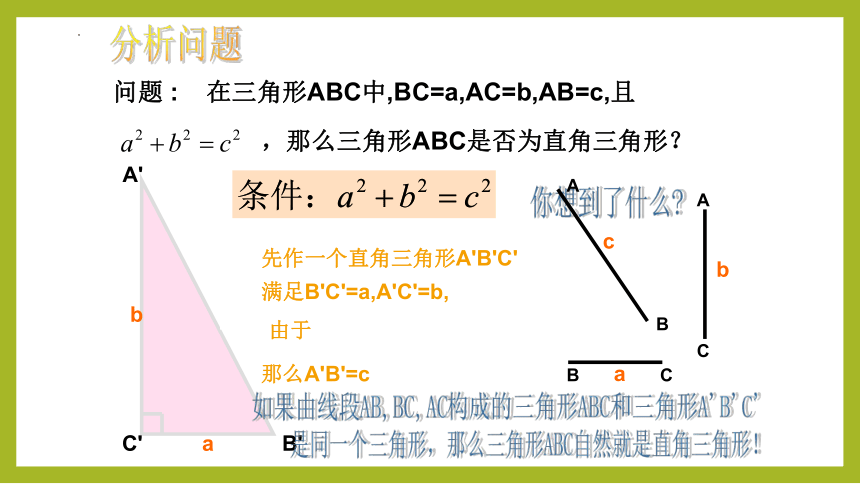
问题 : 在三角形ABC中,BC=a,AC=b,AB=c,且
,那么三角形ABC是否为直角三角形?
C'
A'
B'
a
b
c
先作一个直角三角形A'B'C'
满足B'C'=a,A'C'=b,
那么A'B'=c
你想到了什么
B
C
A
B
A
C
a
b
c
是同一个三角形,那么三角形ABC自然就是直角三角形!
如果由线段AB,BC,AC构成的三角形ABC和三角形A'B'C'
由于
B
A
C
a
b
c
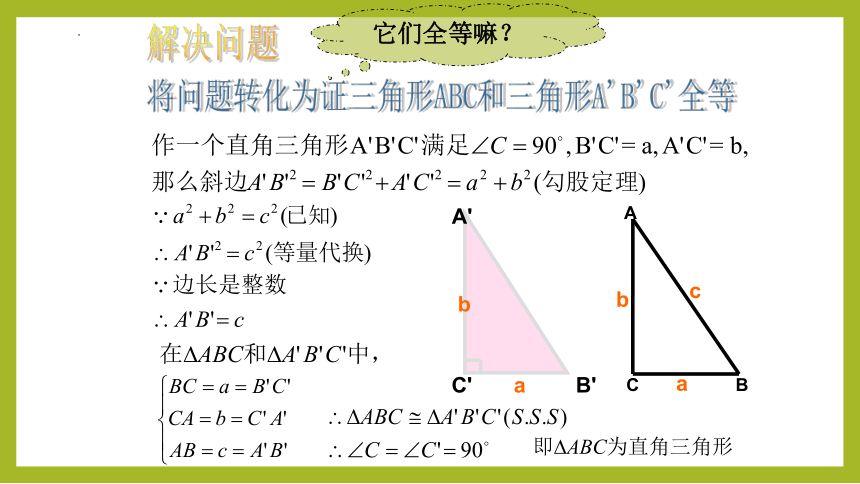
解决问题
将问题转化为证三角形ABC和三角形A'B'C'全等
C'
A'
B'
a
b
它们全等嘛?
结论
在三角形ABC中,BC=a,AC=b,AB=c,且
那么三角形ABC为直角三角形。
如果一个三角形是直角三角形,那么两条直角边的平方和,等于斜边的平方。
如果三角形的一条边的平方等于其他两条边的平方和,那么这个三角形是直角三角形。
由以上证明,我们得出:
题设和结论互换
勾股定理
勾股定理的逆定理
逆命题:第一个命题的题设是第二个命题的结论;第一个命题的结论是第二个命题的题设,这两个命题称为互逆命题。
逆定理:如果一个定理的逆命题经过证明后也是定理,这两个定理互称为逆定理。
结论
勾股定理是直角三角形特有的性质。
C
A
B
a
b
c
勾股定理的逆定理是用来判定三角形
是否为直角三角形的。
B
A
C
a
b
c
例5.三角形三条边长为a,b,c,其中a=8,b=15,c=17,试判断此三角形是否为直角三角形。
解:
因此,这个三角形为直角三角形(勾股定理的逆定理)。
我们发现,通过勾股定理的逆定理,我们可以快速判断一个三角形是否为直角三角形!
A
B
C
D
15
24
20
7
例6.如图为四边形绿地的示意图,求绿地ABCD的面积。
解:联结BD,
在三角形ABD中,
在三角形BCD中,
答:绿地面积为234平方米。
1.判断题:
以0.3、0.4、0.5 为边长的三角形不是直角三角形( )
(2) 以 0.5、1.2、1.3 为边长的三角形是直角三角形.( )
2.在△ABC中,设∠A、 ∠ B、 ∠ C分别所对的边为a、b、c,根据给定条件,判断△ABC 是否是直角三角形.如果是,那么哪一个内角是直角
(1)a=8,b=13,c=11;(2)a=6.5,b=2.5,c=6;(3)a=40,6=41,c=7.
×
√
课本练习
3.如图,△ABC中,已知AB=AC,D是AC上的一点,CD=8,BC=17,BD=15,求AB的长
1 [2022·天津北辰区期末]以下列各组线段为边长作三角形,不能作出直角三角形的是( C )
A.1,2, B.6,8,10
C.3,7,8 D.9,12,15
解析:A.12+22=()2,该组线段能作出直角三角形;B.62+82=102,该组线段能作出直角三角形;C.32+72≠82,该组线段不能作出直角三角形;D.92+122=152,该组线段能作出直角三角形.故选C.
C
随堂检测
2 (易错题)在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,且(a+b)(a-b)=c2,则下列结论正确的是( A )
A.△ABC是直角三角形,且∠A为直角
B.△ABC是直角三角形,且∠B为直角
C.△ABC是直角三角形,且∠C为直角
D.△ABC不是直角三角形
解析:∵(a+b)(a-b)=c2,∴a2-b2=c2,∴a2=b2+c2,∴△ABC是直角三角形,且∠A为直角.故选A.
A
3.一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图2所示,你说这个零件符合要求吗
D
A
B
C
4
3
5
13
12
D
A
B
C
图1
图2
在△BCD中,
所以△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
解:在△ABD中,
所以△ABD 是直角三角形,∠A是直角.
4.一艘在海上朝正北方向航行的轮船,在航行240海里时方位仪坏了,凭经验,船长指挥船左传90°,继续航行70海里,则距出发地250海里,你能判断船转弯后,是否沿正西方向航行?
解:由题意画出相应的图形AB=240海里,BC=70海里,AC=250海里;
在△ABC中AC2-AB2=2502-2402
=4900=702=BC2
即AB2+BC2=AC2∴△ABC是Rt△
答:船转弯后,是沿正西方向航行的。
A
B
C
北
5.如图,哪些是直角三角形,哪些不是,说说你的理由?
①
②
③
④
⑤
⑥
解:
④⑤是直角三角形
①②③⑥不是直角三角形
6.已知△ABC,AB=n -1,BC=2n,AC=n +1(n为大于1的正整数).试问△ABC是直角三角形吗?若是,哪一条边所对的角是直角?请说明理由
先确定AB、BC、AC、
的大小
沪教版八年级上册
第 19 章 几何证明
19.9勾股定理(第3课时)
1.掌握勾股定理逆定理的概念并理解互逆命题、定
理的概念、关系及勾股数.(重点)
2.能证明勾股定理的逆定理,能利用勾股定理的逆
定理判断一个三角形是直角三角形.(难点)
学习目标
a
b
c
C
B
A
勾股定理:
如果直角三角形的两直角边为a,b,斜边长为c ,那么a2+b2=c2.
如果一个三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形.
互逆命题
新课导入
情景引入
同学们你们知道古埃及人用什么方法得到直角的吗
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(13)
(12)
(11)
(10)
(9)
打13个等距的结,把一根绳子分成等长的12段,然后以3段,4段,5段的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
新课导入
思考:从前面我们知道古埃及人认为一个三角形三边长分别为3,4,5,那么这个三角形为直角三角形.按照这种做法真能得到一个直角三角形吗
大禹治水
相传,我国古代的大禹在治水时也用了类似的方法确定直角.
那么,当
①
时,
三角形ABC是直角三角形吗
当然是!
那么,当
三角形ABC是直角三角形吗
②
时,
想一想,猜一猜!
提出问题
C
A
B
a
b
c
分析问题
问题 : 在三角形ABC中,BC=a,AC=b,AB=c,且
,那么三角形ABC是否为直角三角形?
B
C
A
B
A
C
a
b
c
我们要判别三角形ABC是否为直角三角形。
我们要做什么?
我们有什么?
考虑判别在三角形ABC中
是否存在一个内角为90度!
怎么用
分析问题
问题 : 在三角形ABC中,BC=a,AC=b,AB=c,且
,那么三角形ABC是否为直角三角形?
C'
A'
B'
a
b
c
先作一个直角三角形A'B'C'
满足B'C'=a,A'C'=b,
那么A'B'=c
你想到了什么
B
C
A
B
A
C
a
b
c
是同一个三角形,那么三角形ABC自然就是直角三角形!
如果由线段AB,BC,AC构成的三角形ABC和三角形A'B'C'
由于
B
A
C
a
b
c
解决问题
将问题转化为证三角形ABC和三角形A'B'C'全等
C'
A'
B'
a
b
它们全等嘛?
结论
在三角形ABC中,BC=a,AC=b,AB=c,且
那么三角形ABC为直角三角形。
如果一个三角形是直角三角形,那么两条直角边的平方和,等于斜边的平方。
如果三角形的一条边的平方等于其他两条边的平方和,那么这个三角形是直角三角形。
由以上证明,我们得出:
题设和结论互换
勾股定理
勾股定理的逆定理
逆命题:第一个命题的题设是第二个命题的结论;第一个命题的结论是第二个命题的题设,这两个命题称为互逆命题。
逆定理:如果一个定理的逆命题经过证明后也是定理,这两个定理互称为逆定理。
结论
勾股定理是直角三角形特有的性质。
C
A
B
a
b
c
勾股定理的逆定理是用来判定三角形
是否为直角三角形的。
B
A
C
a
b
c
例5.三角形三条边长为a,b,c,其中a=8,b=15,c=17,试判断此三角形是否为直角三角形。
解:
因此,这个三角形为直角三角形(勾股定理的逆定理)。
我们发现,通过勾股定理的逆定理,我们可以快速判断一个三角形是否为直角三角形!
A
B
C
D
15
24
20
7
例6.如图为四边形绿地的示意图,求绿地ABCD的面积。
解:联结BD,
在三角形ABD中,
在三角形BCD中,
答:绿地面积为234平方米。
1.判断题:
以0.3、0.4、0.5 为边长的三角形不是直角三角形( )
(2) 以 0.5、1.2、1.3 为边长的三角形是直角三角形.( )
2.在△ABC中,设∠A、 ∠ B、 ∠ C分别所对的边为a、b、c,根据给定条件,判断△ABC 是否是直角三角形.如果是,那么哪一个内角是直角
(1)a=8,b=13,c=11;(2)a=6.5,b=2.5,c=6;(3)a=40,6=41,c=7.
×
√
课本练习
3.如图,△ABC中,已知AB=AC,D是AC上的一点,CD=8,BC=17,BD=15,求AB的长
1 [2022·天津北辰区期末]以下列各组线段为边长作三角形,不能作出直角三角形的是( C )
A.1,2, B.6,8,10
C.3,7,8 D.9,12,15
解析:A.12+22=()2,该组线段能作出直角三角形;B.62+82=102,该组线段能作出直角三角形;C.32+72≠82,该组线段不能作出直角三角形;D.92+122=152,该组线段能作出直角三角形.故选C.
C
随堂检测
2 (易错题)在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,且(a+b)(a-b)=c2,则下列结论正确的是( A )
A.△ABC是直角三角形,且∠A为直角
B.△ABC是直角三角形,且∠B为直角
C.△ABC是直角三角形,且∠C为直角
D.△ABC不是直角三角形
解析:∵(a+b)(a-b)=c2,∴a2-b2=c2,∴a2=b2+c2,∴△ABC是直角三角形,且∠A为直角.故选A.
A
3.一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图2所示,你说这个零件符合要求吗
D
A
B
C
4
3
5
13
12
D
A
B
C
图1
图2
在△BCD中,
所以△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
解:在△ABD中,
所以△ABD 是直角三角形,∠A是直角.
4.一艘在海上朝正北方向航行的轮船,在航行240海里时方位仪坏了,凭经验,船长指挥船左传90°,继续航行70海里,则距出发地250海里,你能判断船转弯后,是否沿正西方向航行?
解:由题意画出相应的图形AB=240海里,BC=70海里,AC=250海里;
在△ABC中AC2-AB2=2502-2402
=4900=702=BC2
即AB2+BC2=AC2∴△ABC是Rt△
答:船转弯后,是沿正西方向航行的。
A
B
C
北
5.如图,哪些是直角三角形,哪些不是,说说你的理由?
①
②
③
④
⑤
⑥
解:
④⑤是直角三角形
①②③⑥不是直角三角形
6.已知△ABC,AB=n -1,BC=2n,AC=n +1(n为大于1的正整数).试问△ABC是直角三角形吗?若是,哪一条边所对的角是直角?请说明理由
先确定AB、BC、AC、
的大小
