13.1.1 轴对称 课件 25张PPT 人教版八年级数学上册
文档属性
| 名称 | 13.1.1 轴对称 课件 25张PPT 人教版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 767.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 20:58:57 | ||
图片预览





文档简介
(共25张PPT)
第十三章 轴对称
13.1 轴对称
13.1.1 轴对称
学习导航
学习目标
新课导入
概念剖析
典型例题
当堂检测
课堂总结
1.能够识别简单的轴对称图形、两个图形关于直线对称,能指出轴对称图形和两个图形关于直线对称的对称轴和对称点.
2.能通过观察、对比等活动找出轴对称图形与两个图形关于直线对称的区别与联系.
一、学习目标
3.了解垂直平分线的概念和轴对称的性质.
二、新课导入
这些图片什么共同特点?你还能举出其他的例子吗?
三、概念剖析
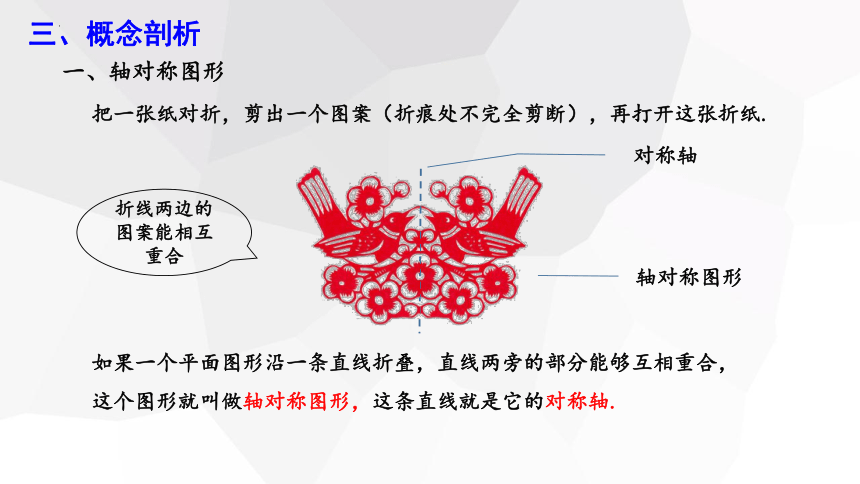
一、轴对称图形
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
折线两边的图案能相互重合
对称轴
轴对称图形
把一张纸对折,剪出一个图案(折痕处不完全剪断),再打开这张折纸.
三、概念剖析
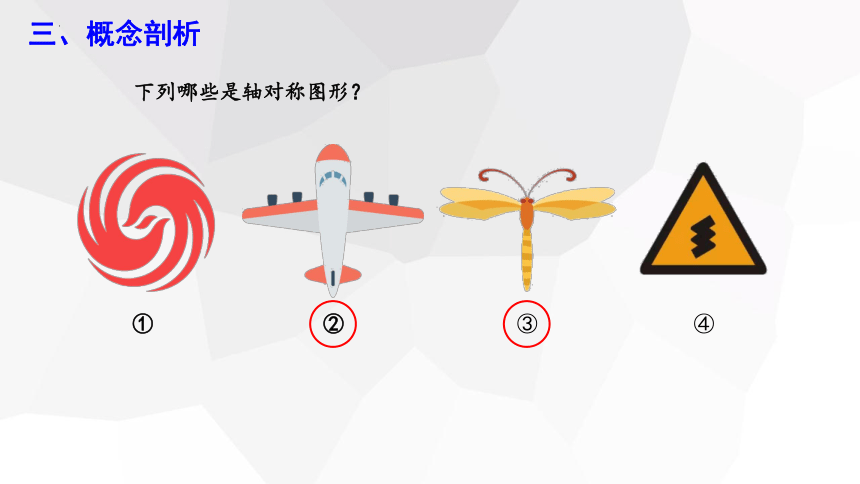
下列哪些是轴对称图形?
①
②
③
④
三、概念剖析
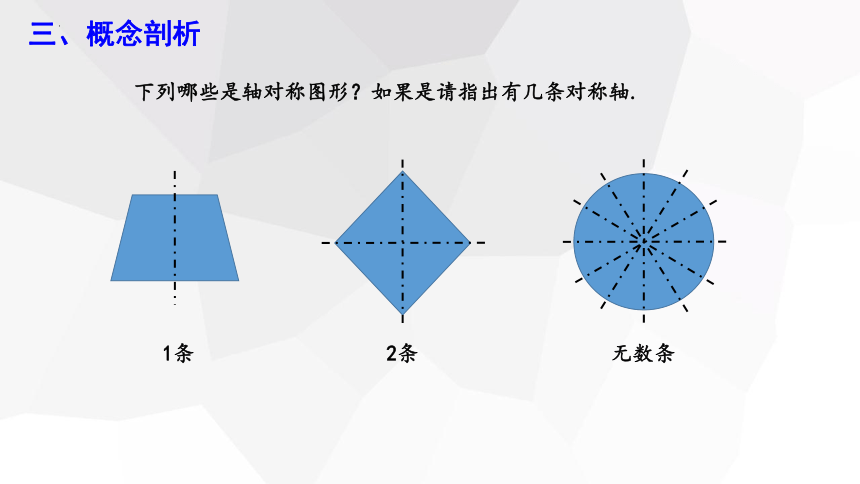
下列哪些是轴对称图形?如果是请指出有几条对称轴.
1条
2条
无数条
三、概念剖析
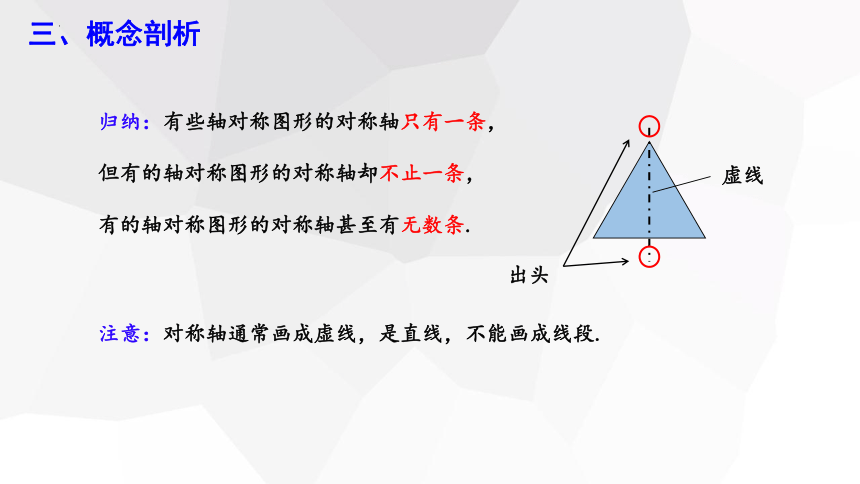
归纳:有些轴对称图形的对称轴只有一条,
但有的轴对称图形的对称轴却不止一条,
有的轴对称图形的对称轴甚至有无数条.
注意:对称轴通常画成虚线,是直线,不能画成线段.
虚线
出头
三、概念剖析
思考:下面的每对图形有什么共同特点
A
B
C
每一对图形沿虚线折叠,左边的图形能与右边的图形重合.
把一个图形沿着一条直线折叠,如果它能与另一个图形重合,那么就说这两个图形关于这条直线成轴对称,这条直线叫做对称轴,
折叠后重合的点是对应点,叫做对称点.
·
A′
B′
·
C′
·
对称点
对称轴
二、轴对称
三、概念剖析
思考:上一章我们学过全等的概念,那么成轴对称的两个图形会全等吗
A
B
C
两个图形沿虚线折叠后,这两个图形能完全重合,说明这两个图形是全等的.
重合
三、概念剖析
观察:轴对称图形和两个图形成轴对称之间的关系
重合
三、概念剖析
观察:轴对称图形和两个图形成轴对称之间的关系
通过观察你能总结归纳出轴对称图形和两个图形成轴对称之间有什么区别和联系吗?
重合
三、概念剖析
区别:
1.轴对称图形是一个图形,两个图形成轴对称是两个图形;
2.轴对称图形可能有多条对称轴,两个图形成轴对称只有一条对称轴.
联系:
1.沿一条直线折叠,直线两旁的部分能够互相重合;
2.都有对称轴;
3.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条直线对称;
如果把两个成轴对称的图形看成一个图形,那么这个图形就是轴对称图形.
三、概念剖析
思考:两个三角形关于直线M对称,点D、E、F分别是点A、B、C的对称点,线段AD、BE、CF与直线M有什么关系?
M
A
B
C
F
D
E
设线段AD与直线M交于P点,
将△ABC沿直线M折叠,点A与D重合,
AP=DP,∠MPA=∠MPD=90°,
点B、C同理,
可以发现线段AD、BE、CF与对称轴垂直相交且中点在对称轴上.
P
·
三、轴对称的性质
三、概念剖析
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
由此我们可以得出图形轴对称的性质:
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
例1.判断下列哪个图形是轴对称图形?并画出对称轴.
四、典型例题
分析:轴对称图形沿对称轴折叠,折叠部分能够互相重合.
解:③存在一条直线使直线两旁的部分沿直线折叠后互相重合,
所以③是轴对称图形;
①②④不存在直线使得图形沿该直线折叠后互相重合,
所以①②④不是轴对称图形.
①
②
③
④
1.下列四个图形中,不是轴对称图形是( )
【当堂检测】
B
2.在等腰三角形、平行四边形、矩形、菱形、正方形、正六边形、圆这7种图形中,一定是轴对称图形的共有_______种.
【当堂检测】
6
分析:直接利用轴对称图形的定义分析得出答案.
正方形、长方形、菱形是特殊的平行四边形,它们是轴对称图形,其它
的平行四边形不是轴对称图形.
一定是轴对称图形的共有等腰三角形、矩形、菱形、正方形、正六边形、
圆6种.
故答案为:6.
例2.如图,已知△ABM和△ACM关于直线AM对称,延长BM、CM,分别交AC、AB于点D、E.请找出图中与DM一定相等的线段,并说明理由.
解:EM=DM,理由如下:
∵△ABM和△ACM关于直线AM对称,
∴∠B=∠C,BM=CM,
在△BME与△CMD中
∴△BME≌△CMD(ASA),
∴EM=DM.
技巧:利用轴对称图形的性质成轴对称的两个图形全等,对称轴垂直平分对称点的连线,进而推导对应的线段、角度相等.
四、典型例题
3.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )
A.AC=A′C′ B.AB∥B′C′
C.AA′⊥MN D.BO=B′O
【当堂检测】
B
分析:根据轴对称的性质对各选项分析判断后利用排除法求解.
∵△ABC与△A′B′C′关于直线MN对称,
∴△ABC≌△A′B′C′,AC=A′C′,AA′⊥MN,BO=B′O,故A、C、D选项正确,
AB∥B′C′不一定成立,故B选项错误,
所以,不一定正确的是B.
4.如图,∠AOB=45°,点P在∠AOB内,且OP=8,点P关于直线OA的对称点P1,点P关于直线OB的对称点P2,连接OP1、OP2、P1P2,则△OP1P2的面积等于_______.
【当堂检测】
32
分析:根据轴对称的性质求出OP1,OP2的长,求出∠P1OP2=90°,根据三角形的面积公式求出即可.
5.如图,∠A=90°,E为BC上的一点,A点和E点关于BD对称;B点、C点关于DE对称,求∠C的度数.
【当堂检测】
解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD.
又B点、C点关于DE对称,
∴∠DBE=∠C,∠ABC=2∠C.
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°,
∴∠C=30°.
四、典型例题
例3.△ABC与△A′B′C′关于直线MN对称,∠C′=90°,∠B=40°,线段AA′长度为4cm,与直线MN相交于P,PQ=5cm,求S△APQ和∠A的度数.
解:∵ △ABC与△A′B′C′关于直线MN对称,
∴△ABC≌△A′B′C′,
又∵点A、B、C的对称点分别是点A′、B′、C′,
∴∠C=∠C′=90°,
又∠B=40°,∴∠A=50°,
对称轴MN是AA′的垂直平分线且AA′=4cm,
∴AP=2cm,又PQ=5cm,
∴S△APQ= ×2×5=5cm2.
A
B
C
N
M
A′
B′
C′
P
Q
6.如图,△ADE和△BDE关于直线DE对称,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是______,若AB=6,则AD=______.
【当堂检测】
13
3
分析:△ADE与△BDE对称,△ADE≌△BDE,
△BEC的周长=BC+BE+EC=AC+BC,
对称轴DE是任何一对对应点所连线段的垂直平分线,
AB=2AD,可求出AD的长度.
五、课堂总结
2.把轴对称的两个图形看成一个整体,它就是一个轴对称图形,把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条轴对称.
3.轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
1.一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴,重合的点是对应点,叫做对称点.
第十三章 轴对称
13.1 轴对称
13.1.1 轴对称
学习导航
学习目标
新课导入
概念剖析
典型例题
当堂检测
课堂总结
1.能够识别简单的轴对称图形、两个图形关于直线对称,能指出轴对称图形和两个图形关于直线对称的对称轴和对称点.
2.能通过观察、对比等活动找出轴对称图形与两个图形关于直线对称的区别与联系.
一、学习目标
3.了解垂直平分线的概念和轴对称的性质.
二、新课导入
这些图片什么共同特点?你还能举出其他的例子吗?
三、概念剖析
一、轴对称图形
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
折线两边的图案能相互重合
对称轴
轴对称图形
把一张纸对折,剪出一个图案(折痕处不完全剪断),再打开这张折纸.
三、概念剖析
下列哪些是轴对称图形?
①
②
③
④
三、概念剖析
下列哪些是轴对称图形?如果是请指出有几条对称轴.
1条
2条
无数条
三、概念剖析
归纳:有些轴对称图形的对称轴只有一条,
但有的轴对称图形的对称轴却不止一条,
有的轴对称图形的对称轴甚至有无数条.
注意:对称轴通常画成虚线,是直线,不能画成线段.
虚线
出头
三、概念剖析
思考:下面的每对图形有什么共同特点
A
B
C
每一对图形沿虚线折叠,左边的图形能与右边的图形重合.
把一个图形沿着一条直线折叠,如果它能与另一个图形重合,那么就说这两个图形关于这条直线成轴对称,这条直线叫做对称轴,
折叠后重合的点是对应点,叫做对称点.
·
A′
B′
·
C′
·
对称点
对称轴
二、轴对称
三、概念剖析
思考:上一章我们学过全等的概念,那么成轴对称的两个图形会全等吗
A
B
C
两个图形沿虚线折叠后,这两个图形能完全重合,说明这两个图形是全等的.
重合
三、概念剖析
观察:轴对称图形和两个图形成轴对称之间的关系
重合
三、概念剖析
观察:轴对称图形和两个图形成轴对称之间的关系
通过观察你能总结归纳出轴对称图形和两个图形成轴对称之间有什么区别和联系吗?
重合
三、概念剖析
区别:
1.轴对称图形是一个图形,两个图形成轴对称是两个图形;
2.轴对称图形可能有多条对称轴,两个图形成轴对称只有一条对称轴.
联系:
1.沿一条直线折叠,直线两旁的部分能够互相重合;
2.都有对称轴;
3.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条直线对称;
如果把两个成轴对称的图形看成一个图形,那么这个图形就是轴对称图形.
三、概念剖析
思考:两个三角形关于直线M对称,点D、E、F分别是点A、B、C的对称点,线段AD、BE、CF与直线M有什么关系?
M
A
B
C
F
D
E
设线段AD与直线M交于P点,
将△ABC沿直线M折叠,点A与D重合,
AP=DP,∠MPA=∠MPD=90°,
点B、C同理,
可以发现线段AD、BE、CF与对称轴垂直相交且中点在对称轴上.
P
·
三、轴对称的性质
三、概念剖析
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
由此我们可以得出图形轴对称的性质:
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
例1.判断下列哪个图形是轴对称图形?并画出对称轴.
四、典型例题
分析:轴对称图形沿对称轴折叠,折叠部分能够互相重合.
解:③存在一条直线使直线两旁的部分沿直线折叠后互相重合,
所以③是轴对称图形;
①②④不存在直线使得图形沿该直线折叠后互相重合,
所以①②④不是轴对称图形.
①
②
③
④
1.下列四个图形中,不是轴对称图形是( )
【当堂检测】
B
2.在等腰三角形、平行四边形、矩形、菱形、正方形、正六边形、圆这7种图形中,一定是轴对称图形的共有_______种.
【当堂检测】
6
分析:直接利用轴对称图形的定义分析得出答案.
正方形、长方形、菱形是特殊的平行四边形,它们是轴对称图形,其它
的平行四边形不是轴对称图形.
一定是轴对称图形的共有等腰三角形、矩形、菱形、正方形、正六边形、
圆6种.
故答案为:6.
例2.如图,已知△ABM和△ACM关于直线AM对称,延长BM、CM,分别交AC、AB于点D、E.请找出图中与DM一定相等的线段,并说明理由.
解:EM=DM,理由如下:
∵△ABM和△ACM关于直线AM对称,
∴∠B=∠C,BM=CM,
在△BME与△CMD中
∴△BME≌△CMD(ASA),
∴EM=DM.
技巧:利用轴对称图形的性质成轴对称的两个图形全等,对称轴垂直平分对称点的连线,进而推导对应的线段、角度相等.
四、典型例题
3.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )
A.AC=A′C′ B.AB∥B′C′
C.AA′⊥MN D.BO=B′O
【当堂检测】
B
分析:根据轴对称的性质对各选项分析判断后利用排除法求解.
∵△ABC与△A′B′C′关于直线MN对称,
∴△ABC≌△A′B′C′,AC=A′C′,AA′⊥MN,BO=B′O,故A、C、D选项正确,
AB∥B′C′不一定成立,故B选项错误,
所以,不一定正确的是B.
4.如图,∠AOB=45°,点P在∠AOB内,且OP=8,点P关于直线OA的对称点P1,点P关于直线OB的对称点P2,连接OP1、OP2、P1P2,则△OP1P2的面积等于_______.
【当堂检测】
32
分析:根据轴对称的性质求出OP1,OP2的长,求出∠P1OP2=90°,根据三角形的面积公式求出即可.
5.如图,∠A=90°,E为BC上的一点,A点和E点关于BD对称;B点、C点关于DE对称,求∠C的度数.
【当堂检测】
解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD.
又B点、C点关于DE对称,
∴∠DBE=∠C,∠ABC=2∠C.
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°,
∴∠C=30°.
四、典型例题
例3.△ABC与△A′B′C′关于直线MN对称,∠C′=90°,∠B=40°,线段AA′长度为4cm,与直线MN相交于P,PQ=5cm,求S△APQ和∠A的度数.
解:∵ △ABC与△A′B′C′关于直线MN对称,
∴△ABC≌△A′B′C′,
又∵点A、B、C的对称点分别是点A′、B′、C′,
∴∠C=∠C′=90°,
又∠B=40°,∴∠A=50°,
对称轴MN是AA′的垂直平分线且AA′=4cm,
∴AP=2cm,又PQ=5cm,
∴S△APQ= ×2×5=5cm2.
A
B
C
N
M
A′
B′
C′
P
Q
6.如图,△ADE和△BDE关于直线DE对称,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是______,若AB=6,则AD=______.
【当堂检测】
13
3
分析:△ADE与△BDE对称,△ADE≌△BDE,
△BEC的周长=BC+BE+EC=AC+BC,
对称轴DE是任何一对对应点所连线段的垂直平分线,
AB=2AD,可求出AD的长度.
五、课堂总结
2.把轴对称的两个图形看成一个整体,它就是一个轴对称图形,把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条轴对称.
3.轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
1.一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴,重合的点是对应点,叫做对称点.
