13.3.1 等腰三角形( 第2课时)课件 19张PPT 人教版八年级数学上册
文档属性
| 名称 | 13.3.1 等腰三角形( 第2课时)课件 19张PPT 人教版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 270.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 21:13:09 | ||
图片预览






文档简介
(共19张PPT)
第十三章 轴对称
13.3.1 等腰三角形
第2课时
学习导航
学习目标
新课导入
概念剖析
典型例题
当堂检测
课堂总结
1.掌握等腰三角形的判定方法.
2.掌握等腰三角形的判定定理,并运用其进行证明和计算.(重点)
一、学习目标
3.了解等腰三角形的尺规作图.
二、新课导入
我们知道,如果一个三角形有两条边相等,那么它们所对的角相等,反过来,如果一个三角形有两个角相等,那么它们所对的边有什么关系?
三、概念剖析
已知:在△ABC中,∠B=∠C(如图).求证:AB=AC.
C
A
B
2
1
D
(
(
在△ABD与△ACD中,
∴△ABD ≌ △ACD.
∴AB=AC(全等三角形的对应边相等).
证明:过A作AD平分∠BAC交BC于点D.
三、概念剖析
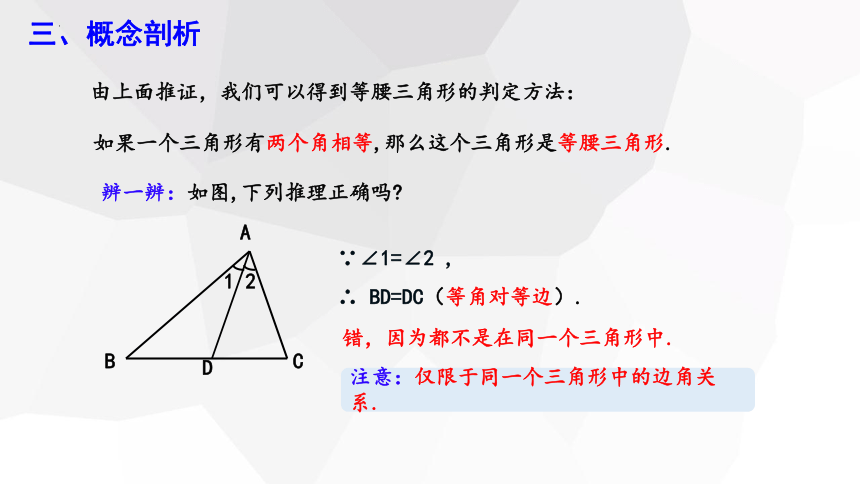
由上面推证,我们可以得到等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.
注意:仅限于同一个三角形中的边角关系.
A
B
C
D
2
1
∵∠1=∠2 , ∴ BD=DC(等角对等边).
辨一辨:如图,下列推理正确吗
错,因为都不是在同一个三角形中.
三、概念剖析
归纳:
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.(简写成“等角对等边”)
A
B
C
∴ AC=AB,(等角对等边)
即△ABC为等腰三角形.
∵∠B=∠C,( 已知 )
在△ABC中,
符号语言:
该判定仅限于同一个三角形中的边角关系,且常用于判定两条线段相等.
例1.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
四、典型例题
分析:要证明AB=AC,
可先证明∠B=∠C,
因为∠1=∠2,
所以可以设法找出∠B,∠C与∠1,∠2的关系.
A
B
C
E
(
(
1
2
D
四、典型例题
证:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).
又∵∠1=∠2,∴∠B=∠C,
∴AB=AC(等角对等边),即△ABC是等腰三角形.
例1.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
A
B
C
E
(
(
1
2
D
1.如图,∠A=36°,∠C=72°,BE为∠ABC的平分线,DE∥BC,则图中等腰三角形的个数有( )
A.6个 B.5个 C.4个 D.3个
【当堂检测】
B
分析:根据三角形内角和定理判定△ABC为等腰三角形,
然后由角平分线、平行线的性质、等角对等边来找图中的等腰三角形.
2.如图,点D是△ABC内部的一点,BD=CD,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,且BE=CF.求证:△ABC为等腰三角形.
【当堂检测】
分析:欲证明AB=AC,只要证明∠ABC=∠ACB即可.
证:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL),
2.如图,点D是△ABC内部的一点,BD=CD,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,且BE=CF.求证:△ABC为等腰三角形.
【当堂检测】
∴∠EBD=∠FCD,
又∵BD=CD,
∴∠DBC=∠DCB,
∴∠DBC+∠EBD=∠DCB+∠FCD,
即∠ABC=∠ACB,
∴AB=AC,△ABC为等腰三角形.
3.如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,BF平分∠ABC交AD于点E,交AC于点F,求证:AE=AF.
【当堂检测】
分析:根据角平分线的定义和余角的性质即可得到结论.
证:∵BF平分∠ABC,
∴∠ABF=∠CBF,
∵∠BAC=90°,AD⊥BC,
∴∠ABF+∠AFB=∠CBF+∠BED=90°,
∴∠AFB=∠BED,
∴∠AFE=∠AEF,
∴AE=AF.
4.将一张长方形纸条ABCD按如图所示折叠,若∠FEC=64°.
(1)求∠1的度数;
【当堂检测】
分析:根据折叠的性质得出∠GEF=64°,利用平行线的性质进行解答即可.
解:∵一张长方形纸条ABCD折叠,
∴∠GEF=∠FEC=64°,
∵AD∥BC,
∴∠1=∠GEB=180°-64°-64°=52°.
4.将一张长方形纸条ABCD按如图所示折叠,若∠FEC=64°.
(2)求证:△EFG是等腰三角形.
【当堂检测】
分析:根据角的度数得出∠GEF=∠GFE,进而证明等腰三角形即可.
证:∵∠FGE=∠1=52°,
∵AD∥BC,
∴∠GFE=∠FEC=64°,
∴∠GEF=∠GFE,
∴GE=GF,
∴△GEF是等腰三角形.
例2.已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形.
作法:(1)作线段AB =a;
(2)作线段AB 的垂直平分线MN,与AB相交于点D;
(3)在MN上取一点C,使DC =h;
(4)连接AC,BC,则△ABC 就是所求作的等腰三角形.
四、典型例题
D
C
A
B
M
N
a
h
5.如图,已知线段a,b,求作等腰三角形,使底边高为a,腰长为b.(a<b,尺规作图,保留作图痕迹)
【当堂检测】
分析:在直线l上取点D,过D点作直线l的垂线,
然后在垂线上截取AD=a,以点A为圆心,b为半径画弧交l于B、C两点,
即可做出满足条件的等腰三角线△ABC.
a
b
解:作直线l在其上取点D,作l′⊥l于D,
在l′上截取AD=a,
然后以点A为圆心,b为半径画弧交l于B、C两点,
连接AB,AC所做出的△ABC满足条件.
5.如图,已知线段a,b,求作等腰三角形,使底边高为a,腰长为b.(a<b,尺规作图,保留作图痕迹).
【当堂检测】
a
b
l
l′
D
A
C
B
·
·
五、课堂总结
如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角对等边”).
等腰三角形的判定:
第十三章 轴对称
13.3.1 等腰三角形
第2课时
学习导航
学习目标
新课导入
概念剖析
典型例题
当堂检测
课堂总结
1.掌握等腰三角形的判定方法.
2.掌握等腰三角形的判定定理,并运用其进行证明和计算.(重点)
一、学习目标
3.了解等腰三角形的尺规作图.
二、新课导入
我们知道,如果一个三角形有两条边相等,那么它们所对的角相等,反过来,如果一个三角形有两个角相等,那么它们所对的边有什么关系?
三、概念剖析
已知:在△ABC中,∠B=∠C(如图).求证:AB=AC.
C
A
B
2
1
D
(
(
在△ABD与△ACD中,
∴△ABD ≌ △ACD.
∴AB=AC(全等三角形的对应边相等).
证明:过A作AD平分∠BAC交BC于点D.
三、概念剖析
由上面推证,我们可以得到等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.
注意:仅限于同一个三角形中的边角关系.
A
B
C
D
2
1
∵∠1=∠2 , ∴ BD=DC(等角对等边).
辨一辨:如图,下列推理正确吗
错,因为都不是在同一个三角形中.
三、概念剖析
归纳:
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.(简写成“等角对等边”)
A
B
C
∴ AC=AB,(等角对等边)
即△ABC为等腰三角形.
∵∠B=∠C,( 已知 )
在△ABC中,
符号语言:
该判定仅限于同一个三角形中的边角关系,且常用于判定两条线段相等.
例1.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
四、典型例题
分析:要证明AB=AC,
可先证明∠B=∠C,
因为∠1=∠2,
所以可以设法找出∠B,∠C与∠1,∠2的关系.
A
B
C
E
(
(
1
2
D
四、典型例题
证:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).
又∵∠1=∠2,∴∠B=∠C,
∴AB=AC(等角对等边),即△ABC是等腰三角形.
例1.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
A
B
C
E
(
(
1
2
D
1.如图,∠A=36°,∠C=72°,BE为∠ABC的平分线,DE∥BC,则图中等腰三角形的个数有( )
A.6个 B.5个 C.4个 D.3个
【当堂检测】
B
分析:根据三角形内角和定理判定△ABC为等腰三角形,
然后由角平分线、平行线的性质、等角对等边来找图中的等腰三角形.
2.如图,点D是△ABC内部的一点,BD=CD,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,且BE=CF.求证:△ABC为等腰三角形.
【当堂检测】
分析:欲证明AB=AC,只要证明∠ABC=∠ACB即可.
证:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL),
2.如图,点D是△ABC内部的一点,BD=CD,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,且BE=CF.求证:△ABC为等腰三角形.
【当堂检测】
∴∠EBD=∠FCD,
又∵BD=CD,
∴∠DBC=∠DCB,
∴∠DBC+∠EBD=∠DCB+∠FCD,
即∠ABC=∠ACB,
∴AB=AC,△ABC为等腰三角形.
3.如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,BF平分∠ABC交AD于点E,交AC于点F,求证:AE=AF.
【当堂检测】
分析:根据角平分线的定义和余角的性质即可得到结论.
证:∵BF平分∠ABC,
∴∠ABF=∠CBF,
∵∠BAC=90°,AD⊥BC,
∴∠ABF+∠AFB=∠CBF+∠BED=90°,
∴∠AFB=∠BED,
∴∠AFE=∠AEF,
∴AE=AF.
4.将一张长方形纸条ABCD按如图所示折叠,若∠FEC=64°.
(1)求∠1的度数;
【当堂检测】
分析:根据折叠的性质得出∠GEF=64°,利用平行线的性质进行解答即可.
解:∵一张长方形纸条ABCD折叠,
∴∠GEF=∠FEC=64°,
∵AD∥BC,
∴∠1=∠GEB=180°-64°-64°=52°.
4.将一张长方形纸条ABCD按如图所示折叠,若∠FEC=64°.
(2)求证:△EFG是等腰三角形.
【当堂检测】
分析:根据角的度数得出∠GEF=∠GFE,进而证明等腰三角形即可.
证:∵∠FGE=∠1=52°,
∵AD∥BC,
∴∠GFE=∠FEC=64°,
∴∠GEF=∠GFE,
∴GE=GF,
∴△GEF是等腰三角形.
例2.已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形.
作法:(1)作线段AB =a;
(2)作线段AB 的垂直平分线MN,与AB相交于点D;
(3)在MN上取一点C,使DC =h;
(4)连接AC,BC,则△ABC 就是所求作的等腰三角形.
四、典型例题
D
C
A
B
M
N
a
h
5.如图,已知线段a,b,求作等腰三角形,使底边高为a,腰长为b.(a<b,尺规作图,保留作图痕迹)
【当堂检测】
分析:在直线l上取点D,过D点作直线l的垂线,
然后在垂线上截取AD=a,以点A为圆心,b为半径画弧交l于B、C两点,
即可做出满足条件的等腰三角线△ABC.
a
b
解:作直线l在其上取点D,作l′⊥l于D,
在l′上截取AD=a,
然后以点A为圆心,b为半径画弧交l于B、C两点,
连接AB,AC所做出的△ABC满足条件.
5.如图,已知线段a,b,求作等腰三角形,使底边高为a,腰长为b.(a<b,尺规作图,保留作图痕迹).
【当堂检测】
a
b
l
l′
D
A
C
B
·
·
五、课堂总结
如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角对等边”).
等腰三角形的判定:
