27.2 相似三角形 同步练习 人教版数学九年级下册(含答案)
文档属性
| 名称 | 27.2 相似三角形 同步练习 人教版数学九年级下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 149.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 21:37:34 | ||
图片预览



文档简介
27.2 相似三角形
一、单选题
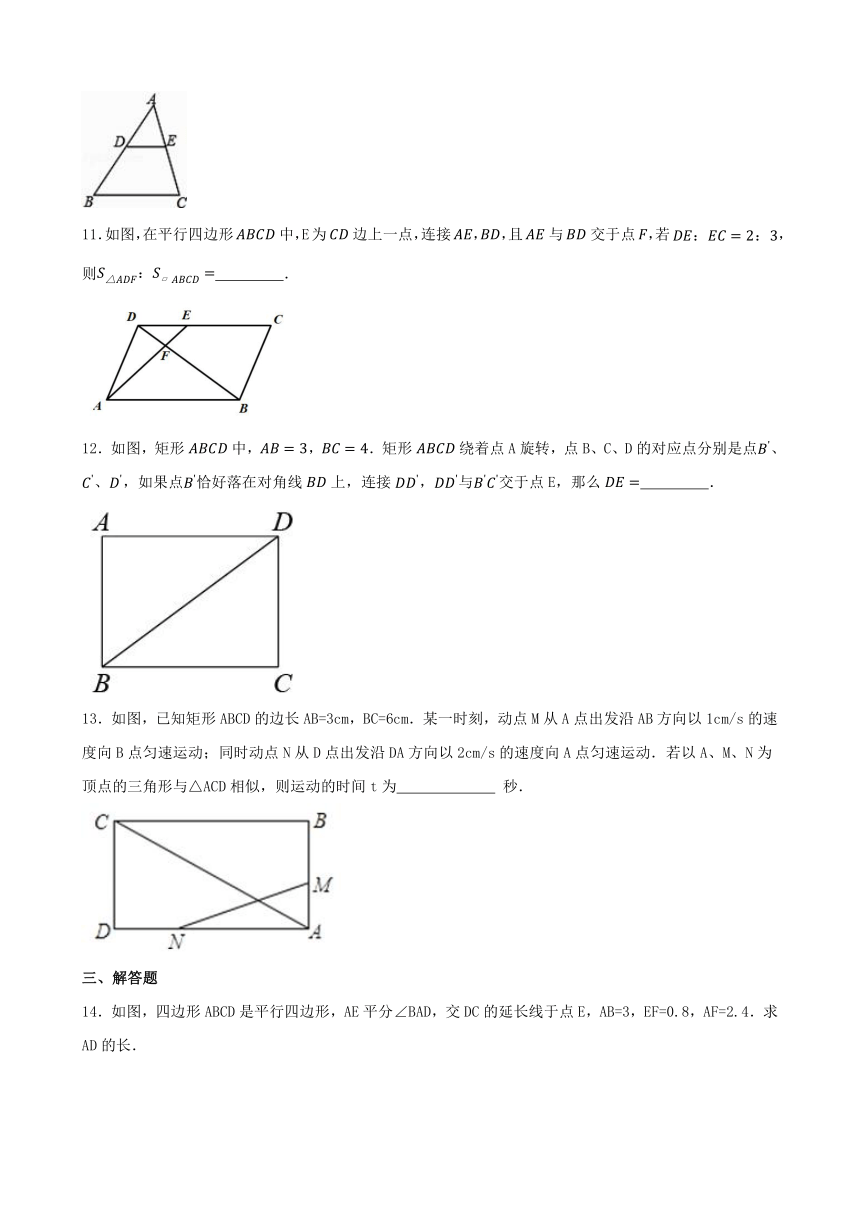
1.如图,□ABCD中,E为AD的中点.已知△DEF的面积为S,则△DCF的面积为( )
A.S B.2S C.3S D.4S
2.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6, ,则EC的长是( ).
A.4.5 B.8 C.10.5 D.14
3.如图,点E为平行四边形ABCD的边AB延长线上的一点,连接DE交BC于点F,则下列结论一定正确的是( )
A. B. C. D.
4.如图,DE是△ABC的中位线,F是DE的中点,BF的延长线交AC于点H,则HE:AH等于( )
A.1:1 B.1:2 C.2:1 D.3:2
5.如图,已知M是 ABCD的AB边的中点,CM交BD于E,则图中阴影部分的面积与 ABCD的面积之比是( )
A. B. C. D.
6.如图,在△ABC中,点D,E分别是AC,AB上的两点,且 = = ,若△ADE的面积为1cm2,则四边形EBCD的面积为( )cm2.
A.2 B.3 C.4 D.5
7.如图,△ABC、△FGH中,D、E两点分别在AB、AC上,F点在DE上,G、H两点在BC上,且DE∥BC,FG∥AB,FH∥AC,若BG:GH:HC=4:6:5,则△ADE与△FGH的面积比为( )
A.4:6 B.9:4 C.5:9 D.5:6
8.如图,在平行四边形ABCD中,E,F分别是边AD,BC的中点,AC分别交BE,DF于G,H,试判断下列结论:①△ABE≌△CDF;②AG=GH=HC;③2EG=BG;④S△ABG:S四边形GHDE=2:3,其中正确的结论是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.已知a,b,c,d是成比例线段,a=3cm,b=2cm,d=6cm,则线段c的长为 cm。
10.如图,在△ABC中,DE∥BC,且AD=2,DB=3,则 = .
11.如图,在平行四边形中,E为边上一点,连接,,且与交于点,若,则 .
12.如图,矩形中,,.矩形绕着点A旋转,点B、C、D的对应点分别是点、、,如果点恰好落在对角线上,连接,与交于点E,那么 .
13.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动.若以A、M、N为顶点的三角形与△ACD相似,则运动的时间t为 秒.
三、解答题
14.如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E,AB=3,EF=0.8,AF=2.4.求AD的长.
15.如图,小明同学用自制的直角三角形纸板 测量树的高度 ,他调整自己的位置,设法使斜边 保持水平,并且边 与点 在同一直线上.已知纸板的两条边 , ,测得边 离地面的高度 , ,求树高 .
16.雯雯和笑笑想利用皮尺和所学的几何知识测量学校操场上旗杆的高度,他们的测量方案如下:当雯雯站在旗杆正前方地面上的点D处时,笑笑在地面上找到一点G,使得点G、雯雯的头顶C以及旗杆的顶部A三点在同一直线上,并测得DG=2.8m;然后雯雯向前移动1.5m到达点F处,笑笑同样在地面上找到一点H,使得点H、雯雯的头顶E以及旗杆的顶部A三点在同一直线上,并测得GH=1.7m,已知图中的所有点均在同一平面内,AB⊥BH,CD⊥BH,EF⊥BH,雯雯的身高CD=EF=1.6m.请你根据以上测量数据,求该校旗杆的高度AB.
17.如图,在 ABCD中,点E、F分别是边AD和对角线AC上的点,连接EF,且∠AEF =∠CAB
(1)求证:ΔAEF∽ΔACD;
(2)若AF=2CF,AE=4、DE=5,求AC的长.
18.如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC、BC及AB的延长线交于点D、E、F,且BF=BC,⊙O是△BEF的外接圆,连接BD.
(1)求证:BD是⊙O的切线;
(2)求证:DE AC=BE CE.
参考答案
1.B
2.B
3.B
4.B
5.C
6.B
7.B
8.D
9.9
10.
11.
12.
13.2.4或1.5
14.解:∵四边形ABCD为平行四边形,
∴AB=DC=3,AB∥DE,
∴△ABF∽△ECF,
∴ .
∵AB=3,EF=0.8,AF=2.4,
∴ ,
∴CE=1,
∴DE=DC+CE=3+1=4.
∵AB∥DE,
∴∠BAE=∠E.
∵AE平分∠BAD,
∴∠BAE=∠DAE.
∴∠E=∠DAE.
∴AD=DE=4.
∴AD的长为4.
15.解:在 中,由勾股得:
即
∴
∵由题意可知: ,
∴
∴
∵ , , ,
∴∴ 米,
∵
∴ 米
答:树高10.5米.
16.解:由题意知,CD=EF=1.6m,DG=2.8m,DF=1.5m,GH=1.7m,
∴FH=2.8﹣1.5+1.7=3m,
∵AB⊥BH,CD⊥BH,EF⊥BH,
∴△CDG∽△ABG,△EFH∽△ABH,
∴,,
∴,即,
解得:BD=21m,
∴,
解得:AB=13.6m.
即该校旗杆的高度AB为13.6m.
17.(1)证明:∵四边形ABCD为平行四边形,
∴ABCD,
∴∠CAB=∠ACD,
∵∠AEF =∠CAB,
∴∠AEF =∠ACD,
∵∠EAF=∠CAD,
∴△AEF∽△ACD;
(2)解:∵△AEF∽△ACD
∴
∵AF=2CF,
∴
AE=4、DE=5,
解得3(负值舍去)
18.(1)证明:如图,连接OB,
∵OB=OC,
∴∠2=∠3,
∵∠ABC=90°、D为AC的中点,
∴AD=CD=BD,∠3+∠4=90°,
∴∠1=∠5,
又∵∠ADF=∠ABC=90°,
∴∠1=90°﹣∠A、∠2=90°﹣∠A,
∴∠1=∠2,
则∠5=∠3,
∴∠5+∠4=90°,
∴BD是⊙O的切线;
(2)证明:在△ABC和△EBF中,
∵ ,
∴△ABC≌△EBF(ASA),
∴AB=BE,
∵∠ABC=∠EDC=90°,∠ACB=∠ECD,
∴△ABC∽△EDC,
∴ = ,即AB CE=DE AC,
∴BE CE=DE AC
一、单选题
1.如图,□ABCD中,E为AD的中点.已知△DEF的面积为S,则△DCF的面积为( )
A.S B.2S C.3S D.4S
2.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6, ,则EC的长是( ).
A.4.5 B.8 C.10.5 D.14
3.如图,点E为平行四边形ABCD的边AB延长线上的一点,连接DE交BC于点F,则下列结论一定正确的是( )
A. B. C. D.
4.如图,DE是△ABC的中位线,F是DE的中点,BF的延长线交AC于点H,则HE:AH等于( )
A.1:1 B.1:2 C.2:1 D.3:2
5.如图,已知M是 ABCD的AB边的中点,CM交BD于E,则图中阴影部分的面积与 ABCD的面积之比是( )
A. B. C. D.
6.如图,在△ABC中,点D,E分别是AC,AB上的两点,且 = = ,若△ADE的面积为1cm2,则四边形EBCD的面积为( )cm2.
A.2 B.3 C.4 D.5
7.如图,△ABC、△FGH中,D、E两点分别在AB、AC上,F点在DE上,G、H两点在BC上,且DE∥BC,FG∥AB,FH∥AC,若BG:GH:HC=4:6:5,则△ADE与△FGH的面积比为( )
A.4:6 B.9:4 C.5:9 D.5:6
8.如图,在平行四边形ABCD中,E,F分别是边AD,BC的中点,AC分别交BE,DF于G,H,试判断下列结论:①△ABE≌△CDF;②AG=GH=HC;③2EG=BG;④S△ABG:S四边形GHDE=2:3,其中正确的结论是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.已知a,b,c,d是成比例线段,a=3cm,b=2cm,d=6cm,则线段c的长为 cm。
10.如图,在△ABC中,DE∥BC,且AD=2,DB=3,则 = .
11.如图,在平行四边形中,E为边上一点,连接,,且与交于点,若,则 .
12.如图,矩形中,,.矩形绕着点A旋转,点B、C、D的对应点分别是点、、,如果点恰好落在对角线上,连接,与交于点E,那么 .
13.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动.若以A、M、N为顶点的三角形与△ACD相似,则运动的时间t为 秒.
三、解答题
14.如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E,AB=3,EF=0.8,AF=2.4.求AD的长.
15.如图,小明同学用自制的直角三角形纸板 测量树的高度 ,他调整自己的位置,设法使斜边 保持水平,并且边 与点 在同一直线上.已知纸板的两条边 , ,测得边 离地面的高度 , ,求树高 .
16.雯雯和笑笑想利用皮尺和所学的几何知识测量学校操场上旗杆的高度,他们的测量方案如下:当雯雯站在旗杆正前方地面上的点D处时,笑笑在地面上找到一点G,使得点G、雯雯的头顶C以及旗杆的顶部A三点在同一直线上,并测得DG=2.8m;然后雯雯向前移动1.5m到达点F处,笑笑同样在地面上找到一点H,使得点H、雯雯的头顶E以及旗杆的顶部A三点在同一直线上,并测得GH=1.7m,已知图中的所有点均在同一平面内,AB⊥BH,CD⊥BH,EF⊥BH,雯雯的身高CD=EF=1.6m.请你根据以上测量数据,求该校旗杆的高度AB.
17.如图,在 ABCD中,点E、F分别是边AD和对角线AC上的点,连接EF,且∠AEF =∠CAB
(1)求证:ΔAEF∽ΔACD;
(2)若AF=2CF,AE=4、DE=5,求AC的长.
18.如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC、BC及AB的延长线交于点D、E、F,且BF=BC,⊙O是△BEF的外接圆,连接BD.
(1)求证:BD是⊙O的切线;
(2)求证:DE AC=BE CE.
参考答案
1.B
2.B
3.B
4.B
5.C
6.B
7.B
8.D
9.9
10.
11.
12.
13.2.4或1.5
14.解:∵四边形ABCD为平行四边形,
∴AB=DC=3,AB∥DE,
∴△ABF∽△ECF,
∴ .
∵AB=3,EF=0.8,AF=2.4,
∴ ,
∴CE=1,
∴DE=DC+CE=3+1=4.
∵AB∥DE,
∴∠BAE=∠E.
∵AE平分∠BAD,
∴∠BAE=∠DAE.
∴∠E=∠DAE.
∴AD=DE=4.
∴AD的长为4.
15.解:在 中,由勾股得:
即
∴
∵由题意可知: ,
∴
∴
∵ , , ,
∴∴ 米,
∵
∴ 米
答:树高10.5米.
16.解:由题意知,CD=EF=1.6m,DG=2.8m,DF=1.5m,GH=1.7m,
∴FH=2.8﹣1.5+1.7=3m,
∵AB⊥BH,CD⊥BH,EF⊥BH,
∴△CDG∽△ABG,△EFH∽△ABH,
∴,,
∴,即,
解得:BD=21m,
∴,
解得:AB=13.6m.
即该校旗杆的高度AB为13.6m.
17.(1)证明:∵四边形ABCD为平行四边形,
∴ABCD,
∴∠CAB=∠ACD,
∵∠AEF =∠CAB,
∴∠AEF =∠ACD,
∵∠EAF=∠CAD,
∴△AEF∽△ACD;
(2)解:∵△AEF∽△ACD
∴
∵AF=2CF,
∴
AE=4、DE=5,
解得3(负值舍去)
18.(1)证明:如图,连接OB,
∵OB=OC,
∴∠2=∠3,
∵∠ABC=90°、D为AC的中点,
∴AD=CD=BD,∠3+∠4=90°,
∴∠1=∠5,
又∵∠ADF=∠ABC=90°,
∴∠1=90°﹣∠A、∠2=90°﹣∠A,
∴∠1=∠2,
则∠5=∠3,
∴∠5+∠4=90°,
∴BD是⊙O的切线;
(2)证明:在△ABC和△EBF中,
∵ ,
∴△ABC≌△EBF(ASA),
∴AB=BE,
∵∠ABC=∠EDC=90°,∠ACB=∠ECD,
∴△ABC∽△EDC,
∴ = ,即AB CE=DE AC,
∴BE CE=DE AC
