2.2 用配方法求解一元二次方程 第1课时课件(共15张PPT)2023-2024学年北师大版九年级上册数学
文档属性
| 名称 | 2.2 用配方法求解一元二次方程 第1课时课件(共15张PPT)2023-2024学年北师大版九年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
2.2 用配方法求解一元二次方程
第1课时
第二章 一元二次方程
1.会用直接开平方法解形如(x+m)2=n(n≥0)的方程.
2.会用配方法解二次项系数为1的一元二次方程.
任务一:会用直接开平方法解形如(x+m)2=n(n≥0)的方程
活动:解下列方程.
解:(1)∵x2=4,
开平方,得x=±2.
(2)∵x2=5,
开平方,得x=± .
(3)∵(x+2)2=5,
开平方,得x+2=± ,
∴x+2= 或x+2=- ,
∴x= -2或x=- -2.
把(x+2)看成一个整体
对于形如x2 =a(a≥0)的方程,根据平方根的定义,可解得 ,这种解一元二次方程的方法叫做开平方法.
思考:a可以是负数吗?
用直接开平方法还可以解形如(x+m)2=n(n≥0)方程
从(x+m)2=n x+m=
实质上:一元二次方程 两个一元一次方程
变形
转化
练一练
利用直接开平方法解下列方程:
(1)(2x+3)2=24; (2)(x-2)2=3.
解:(1)开平方,得2x+3= ,
解得x1= ,x2= .
(2)两边同时乘以3,得(x-2)2=9,
开平方,得x-2=±3,
解得x1=5,x2=-1.
任务二:会用配方法解二次项系数为1的一元二次方程
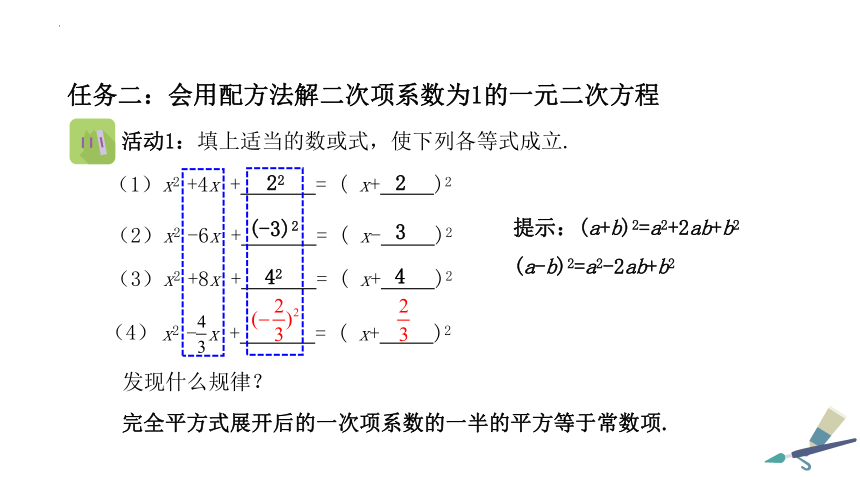
活动1:填上适当的数或式,使下列各等式成立.
(1)x2 +4x + = ( x+ )2
(2)x2 -6x + = ( x- )2
(3)x2 +8x + = ( x+ )2
x2 - x + = ( x+ )2
22
2
(-3)2
3
42
4
(4)
发现什么规律?
完全平方式展开后的一次项系数的一半的平方等于常数项.
提示:(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
形如 x2+bx 的式子,加上一次项系数b的一半的平方,则可配成完全平方式,即
通过配成完全平方式的方法得到了一元二次方程的根,这种解一元二次方程的方法称为配方法.
新知生成
x2 + bx + ( )2 = ( x + )2
活动2:解方程x2+14x+9=0.
解:把常数项移到方程的右边,得
x2+14x=-9 ,
两边都加49(一次项系数14的一半的平方),得
x2+14x+49=-9+49,
即(x+7)2=40 .
两边开平方,得x+7=± ,
即x+7= 或x+7=- .
所以x1= -7,x2=- -7.
活动探究
学习目标
当堂检测
课堂总结
试一试:用配方法解决梯子底部滑动问题:x2 + 12x -15=0 .
试总结用配方法解一元二次方程的步骤.
解:可以把常数项移到方程的右边,得x2+12x=15 ,
两边都加62(一次项系数6的一半的平方),得
x2+12x+62=15+62,
即(x+6)2=51.
两边开平方,得x+6= ,
即x+6= 或x+6= .
所以x1= , x2= .
归纳总结
利用配方法解一元二次方程的步骤:
(1)移项:把常数项移到方程的右边;
(2)配方:方程两边都加上一次项系数一半的平方;
(3)变形:方程左边写成完全平方式,右边合并同类项;
(4)开方:根据平方根的概念,将一元二次方程转化为两个一元一次方程;
(5)求解:解一元一次方程;
(6)定解:写出原方程的解.
活动探究
学习目标
当堂检测
课堂总结
练一练
如果x2-8x+m=0可以通过配方写成(x-n)2=6的形式,那么m、n的值分别为( )
A.10,-4 B.-10,4
C.10,4 D.-10,-4
C
C.4(x-1)2=9,解方程,得4(x-1)=±3, x1= ;
x2=
D.(2x+3)2=25,解方程,得2x+3=±5, x1=1;x2=-4
1.下列解方程的过程中,正确的是( )
A.x2=-2,解方程,得x=±
B.(x-2)2=4,解方程,得x-2=2,x=4
D
2.用配方法解关于x的一元二次方程x2-2x-3=0,配方后的方程可以是( )
A.(x-1)2=4 B.(x+1)2=4
C.(x-1)2=16 D.(x+1)2=16
A
3.用配方法解一元二次方程:
(1)y2-6y+6=0; (2)x2-10x=24.
解:(1)由原式配方,得(y-3)2=3.
故y-3=± .
则y1=3+ ,y2=3- .
(2)由原式配方,得(x-5)2=49.
则x-5=±7.
则x1=12,x2=-2.
针对本节课所学内容,说说你都学到了哪些知识?
用配方法解
一元二次方程
直接开平方法:
基本思路:
解二次项系数为1的一元二次方程步骤
形如(x + m)2 = n (n≥0)
将方程转化为(x + m)2 = n
(n≥0)的形式,再用直接开平方法,
直接求根.
1.移项
3.直接开平方求解
2.配方
2.2 用配方法求解一元二次方程
第1课时
第二章 一元二次方程
1.会用直接开平方法解形如(x+m)2=n(n≥0)的方程.
2.会用配方法解二次项系数为1的一元二次方程.
任务一:会用直接开平方法解形如(x+m)2=n(n≥0)的方程
活动:解下列方程.
解:(1)∵x2=4,
开平方,得x=±2.
(2)∵x2=5,
开平方,得x=± .
(3)∵(x+2)2=5,
开平方,得x+2=± ,
∴x+2= 或x+2=- ,
∴x= -2或x=- -2.
把(x+2)看成一个整体
对于形如x2 =a(a≥0)的方程,根据平方根的定义,可解得 ,这种解一元二次方程的方法叫做开平方法.
思考:a可以是负数吗?
用直接开平方法还可以解形如(x+m)2=n(n≥0)方程
从(x+m)2=n x+m=
实质上:一元二次方程 两个一元一次方程
变形
转化
练一练
利用直接开平方法解下列方程:
(1)(2x+3)2=24; (2)(x-2)2=3.
解:(1)开平方,得2x+3= ,
解得x1= ,x2= .
(2)两边同时乘以3,得(x-2)2=9,
开平方,得x-2=±3,
解得x1=5,x2=-1.
任务二:会用配方法解二次项系数为1的一元二次方程
活动1:填上适当的数或式,使下列各等式成立.
(1)x2 +4x + = ( x+ )2
(2)x2 -6x + = ( x- )2
(3)x2 +8x + = ( x+ )2
x2 - x + = ( x+ )2
22
2
(-3)2
3
42
4
(4)
发现什么规律?
完全平方式展开后的一次项系数的一半的平方等于常数项.
提示:(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
形如 x2+bx 的式子,加上一次项系数b的一半的平方,则可配成完全平方式,即
通过配成完全平方式的方法得到了一元二次方程的根,这种解一元二次方程的方法称为配方法.
新知生成
x2 + bx + ( )2 = ( x + )2
活动2:解方程x2+14x+9=0.
解:把常数项移到方程的右边,得
x2+14x=-9 ,
两边都加49(一次项系数14的一半的平方),得
x2+14x+49=-9+49,
即(x+7)2=40 .
两边开平方,得x+7=± ,
即x+7= 或x+7=- .
所以x1= -7,x2=- -7.
活动探究
学习目标
当堂检测
课堂总结
试一试:用配方法解决梯子底部滑动问题:x2 + 12x -15=0 .
试总结用配方法解一元二次方程的步骤.
解:可以把常数项移到方程的右边,得x2+12x=15 ,
两边都加62(一次项系数6的一半的平方),得
x2+12x+62=15+62,
即(x+6)2=51.
两边开平方,得x+6= ,
即x+6= 或x+6= .
所以x1= , x2= .
归纳总结
利用配方法解一元二次方程的步骤:
(1)移项:把常数项移到方程的右边;
(2)配方:方程两边都加上一次项系数一半的平方;
(3)变形:方程左边写成完全平方式,右边合并同类项;
(4)开方:根据平方根的概念,将一元二次方程转化为两个一元一次方程;
(5)求解:解一元一次方程;
(6)定解:写出原方程的解.
活动探究
学习目标
当堂检测
课堂总结
练一练
如果x2-8x+m=0可以通过配方写成(x-n)2=6的形式,那么m、n的值分别为( )
A.10,-4 B.-10,4
C.10,4 D.-10,-4
C
C.4(x-1)2=9,解方程,得4(x-1)=±3, x1= ;
x2=
D.(2x+3)2=25,解方程,得2x+3=±5, x1=1;x2=-4
1.下列解方程的过程中,正确的是( )
A.x2=-2,解方程,得x=±
B.(x-2)2=4,解方程,得x-2=2,x=4
D
2.用配方法解关于x的一元二次方程x2-2x-3=0,配方后的方程可以是( )
A.(x-1)2=4 B.(x+1)2=4
C.(x-1)2=16 D.(x+1)2=16
A
3.用配方法解一元二次方程:
(1)y2-6y+6=0; (2)x2-10x=24.
解:(1)由原式配方,得(y-3)2=3.
故y-3=± .
则y1=3+ ,y2=3- .
(2)由原式配方,得(x-5)2=49.
则x-5=±7.
则x1=12,x2=-2.
针对本节课所学内容,说说你都学到了哪些知识?
用配方法解
一元二次方程
直接开平方法:
基本思路:
解二次项系数为1的一元二次方程步骤
形如(x + m)2 = n (n≥0)
将方程转化为(x + m)2 = n
(n≥0)的形式,再用直接开平方法,
直接求根.
1.移项
3.直接开平方求解
2.配方
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
