3.4相似三角形的判定与性质分层练习(含答案)
文档属性
| 名称 | 3.4相似三角形的判定与性质分层练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 707.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-09-19 09:59:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
3.4相似三角形的判定与性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在△ABC中,点D,E分别在AB,AC上,若DEBC,=,DE=6cm,则BC的长为( )
A.9cm B.12cm C.15cm D.18cm
2.如图,在等边中,D为边上一点,E为边上一点,且,,,则的边长为( )
A.9 B.12 C.16 D.18
3.两个相似三角形的面积比为,那么它们的对应边的比为( )
A.1:16 B.16:1 C.1:2 D.2:1
4.如图在中,,,,垂足分别为、.则与(本身除外)相似的三角形共有( )
A.4个 B.3个 C.2个 D.1个
5.如图,在平行四边形中,E,F分别为的中点,连接.若的面积为S,则的面积为( )
A. B. C. D.S
6.如图,是等边三角形,被一矩形所截,被截成三等分,,若图中阴影部分的面积是12,则四边形的面积为( )
A.16 B.20 C.36 D.40
7.如图,的顶点B在反比例函数的图象上,边在x轴上,已知,,,则图中阴影部分的面积是( )
A.12 B. C. D.
8.如图,,在边上取点P,使得与相似,则满足条件的点P有( )
A.1个 B.2个 C.3个 D.0个
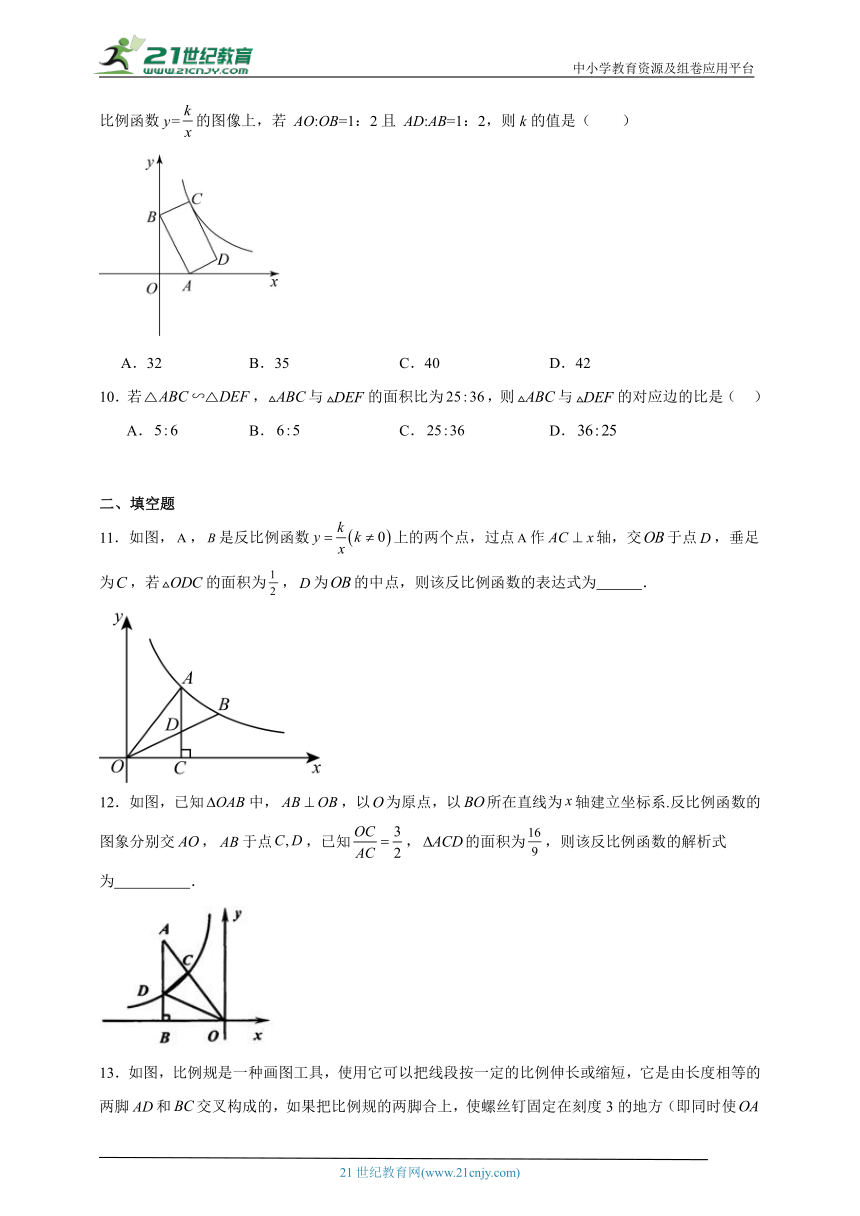
9.如图,在平面直角坐标系xOy中, 四边形ABCD是矩形,点A的坐标为(4,0),顶点C在反比例函数y=的图像上,若 AO:OB=1:2且 AD:AB=1:2,则k的值是( )
A.32 B.35 C.40 D.42
10.若,与的面积比为,则与的对应边的比是( )
A. B. C. D.
二、填空题
11.如图,,是反比例函数上的两个点,过点作轴,交于点,垂足为,若的面积为,为的中点,则该反比例函数的表达式为 .
12.如图,已知中,,以为原点,以所在直线为轴建立坐标系.反比例函数的图象分别交,于点,已知,的面积为,则该反比例函数的解析式为 .
13.如图,比例规是一种画图工具,使用它可以把线段按一定的比例伸长或缩短,它是由长度相等的两脚和交叉构成的,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使=3,=3),然后张开两脚,使、两个尖端分别在线段l的两端上,若=2,则的长是 .
14.如图,M是AC的中点,AB=8,AC=10,当AN= 时,△ABC∽△AMN.
15.如图,在中,是的中点,延长至点,使,延长交于点,则的值为 .
16.如图,在矩形ABCD中,AB=5,BC=8,在AB的右侧有一点E,且AE=AB,BE=BC,则CE= .
17.如图,正方形ABCD中,点E为AB的中点,M、N分别为AD、BC上的点,若,,,则MN的长为 .
18.已知,如图和是的两条高,交于点F,,,,则的长为 .
19.在中,,,,点P是射线AB上一点,且的三边之比为,则AP的长为 .
20.如图,在边长为7的正方形ABCD中放入四个小正方形后形成一个中心对称图形,其中两顶点E,F分别在边BC,AD上,则放入的四个小正方形的面积之和为 .
三、解答题
21.如图,在正方形中,为边的中点,点在边上,且,延长F交的延长线于点G.
(1)求证:;
(2)若,求的长.
22.如图1,已知在矩形ABCD中,AD=10,E是CD上一点,且DE=5,点P是BC上一点,PA=10,∠PAD=2∠DAE.
(1)求证:∠APE=90°;
(2)求AB的长;
(3)如图2,点F在BC边上且CF=4,点Q是边BC上的一动点,且从点C向点B方向运动.连接DQ,M是DQ的中点,将点M绕点Q逆时针旋转90°,点M的对应点是M′,在点Q的运动过程中,①判断∠M′FB是否为定值?若是说明理由.②求AM′的最小值.
23.如图,在中,点在上,连接,点在上,的延长线交射线于点.
(1)若点是边上的中点,且,求的值.
(2)若点是边上的中点,且,求的值.(用含的代数式表示),试写出解答过程.
(3)探究三:若,且,请直接写出的值(不写解答过程).
24.如图,已知中,D、E、F分别是边上的点,且.
(1)设,.试用,表示;
(2)如果的面积是16,求四边形的面积.
25.如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O, 则等于
参考答案:
1.C
2.A
3.C
4.A
5.B
6.B
7.C
8.C
9.C
10.A
11.
12.
13.6
14.
15.
16.
17.9
18.或
19.5或11或20
20.22
21.(1)略
(2)12
22.(1)略;(2)AB=8;(3)①∠M′FB为定值;②当AM'⊥FM'时,AM'的值最小,AM'=2.
23.(1)2;(2);(3)
24.(1)
(2)6
25.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.4相似三角形的判定与性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在△ABC中,点D,E分别在AB,AC上,若DEBC,=,DE=6cm,则BC的长为( )
A.9cm B.12cm C.15cm D.18cm
2.如图,在等边中,D为边上一点,E为边上一点,且,,,则的边长为( )
A.9 B.12 C.16 D.18
3.两个相似三角形的面积比为,那么它们的对应边的比为( )
A.1:16 B.16:1 C.1:2 D.2:1
4.如图在中,,,,垂足分别为、.则与(本身除外)相似的三角形共有( )
A.4个 B.3个 C.2个 D.1个
5.如图,在平行四边形中,E,F分别为的中点,连接.若的面积为S,则的面积为( )
A. B. C. D.S
6.如图,是等边三角形,被一矩形所截,被截成三等分,,若图中阴影部分的面积是12,则四边形的面积为( )
A.16 B.20 C.36 D.40
7.如图,的顶点B在反比例函数的图象上,边在x轴上,已知,,,则图中阴影部分的面积是( )
A.12 B. C. D.
8.如图,,在边上取点P,使得与相似,则满足条件的点P有( )
A.1个 B.2个 C.3个 D.0个
9.如图,在平面直角坐标系xOy中, 四边形ABCD是矩形,点A的坐标为(4,0),顶点C在反比例函数y=的图像上,若 AO:OB=1:2且 AD:AB=1:2,则k的值是( )
A.32 B.35 C.40 D.42
10.若,与的面积比为,则与的对应边的比是( )
A. B. C. D.
二、填空题
11.如图,,是反比例函数上的两个点,过点作轴,交于点,垂足为,若的面积为,为的中点,则该反比例函数的表达式为 .
12.如图,已知中,,以为原点,以所在直线为轴建立坐标系.反比例函数的图象分别交,于点,已知,的面积为,则该反比例函数的解析式为 .
13.如图,比例规是一种画图工具,使用它可以把线段按一定的比例伸长或缩短,它是由长度相等的两脚和交叉构成的,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使=3,=3),然后张开两脚,使、两个尖端分别在线段l的两端上,若=2,则的长是 .
14.如图,M是AC的中点,AB=8,AC=10,当AN= 时,△ABC∽△AMN.
15.如图,在中,是的中点,延长至点,使,延长交于点,则的值为 .
16.如图,在矩形ABCD中,AB=5,BC=8,在AB的右侧有一点E,且AE=AB,BE=BC,则CE= .
17.如图,正方形ABCD中,点E为AB的中点,M、N分别为AD、BC上的点,若,,,则MN的长为 .
18.已知,如图和是的两条高,交于点F,,,,则的长为 .
19.在中,,,,点P是射线AB上一点,且的三边之比为,则AP的长为 .
20.如图,在边长为7的正方形ABCD中放入四个小正方形后形成一个中心对称图形,其中两顶点E,F分别在边BC,AD上,则放入的四个小正方形的面积之和为 .
三、解答题
21.如图,在正方形中,为边的中点,点在边上,且,延长F交的延长线于点G.
(1)求证:;
(2)若,求的长.
22.如图1,已知在矩形ABCD中,AD=10,E是CD上一点,且DE=5,点P是BC上一点,PA=10,∠PAD=2∠DAE.
(1)求证:∠APE=90°;
(2)求AB的长;
(3)如图2,点F在BC边上且CF=4,点Q是边BC上的一动点,且从点C向点B方向运动.连接DQ,M是DQ的中点,将点M绕点Q逆时针旋转90°,点M的对应点是M′,在点Q的运动过程中,①判断∠M′FB是否为定值?若是说明理由.②求AM′的最小值.
23.如图,在中,点在上,连接,点在上,的延长线交射线于点.
(1)若点是边上的中点,且,求的值.
(2)若点是边上的中点,且,求的值.(用含的代数式表示),试写出解答过程.
(3)探究三:若,且,请直接写出的值(不写解答过程).
24.如图,已知中,D、E、F分别是边上的点,且.
(1)设,.试用,表示;
(2)如果的面积是16,求四边形的面积.
25.如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O, 则等于
参考答案:
1.C
2.A
3.C
4.A
5.B
6.B
7.C
8.C
9.C
10.A
11.
12.
13.6
14.
15.
16.
17.9
18.或
19.5或11或20
20.22
21.(1)略
(2)12
22.(1)略;(2)AB=8;(3)①∠M′FB为定值;②当AM'⊥FM'时,AM'的值最小,AM'=2.
23.(1)2;(2);(3)
24.(1)
(2)6
25.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
