5.1 总体平均数与方差的估计分层练习(含答案)
文档属性
| 名称 | 5.1 总体平均数与方差的估计分层练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 489.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-09-19 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
5.1总体平均数与方差的估计
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在测量某物理量的过程中,因为仪器和观察的误差,使得次测量分别得到共个数据,我们规定所测得的物理量的“最佳近似值”是这样一个数据:与其他近似值比较,与各个数据差的平方和最小.若三次测量得到的数据依次为,依据此规定,那么本次测量的“最佳近似值”为( )
A.1.21 B.1.25 C.1.22 D.1.23
2.下列说法正确的是( )
A.的算术平方根是9
B.一组数据的极差、方差或标准差越小,这组数据就越稳定
C.三角形的一个外角等于它的两个内角之和
D.立方根等于自身的数有1和0
3.在一次数学竞赛活动中,五位同学答对题目的个数分别为7,5,3,5,10.则关于这组数据的结论不正确的是( )
A.众数是5 B.平均数是6 C.中位数是5 D.中位数是3
4.在社会实践活动中,某中学对甲、乙、丙、丁四个超市三月份的苹果价格进行调查,它们的价格的平均值均为元,方差分别为,,,.三月份苹果价格最稳定的超市是( )
A.甲 B.乙 C.丙 D.丁
5.数据是某班六位同学定点投篮(每人投10个)的情况,投进篮筐的个数为6,9,8,4,0,3,这组数据的平均数、中位数和极差分别是( )
A.6,6,9 B.6,5,9 C.5,6,6 D.5,5,9
6.若1,2,3,x的平均数是6.且1,2,3,x,y的平均数是7,则y的值为( )
A.7 B.9 C.11 D.13
7.有一句地方民谣“早穿皮袄午穿纱”,说明此地气温的下列特征数中,较大的是( )
A.极差 B.平均数 C.众数 D.中位数
8.教练组对运动员正式比赛前的5次训练成绩进行分析,判断谁的成绩更加稳定,一般需要考察这5次成绩的 ( )
A.平均数或中位数 B.众数或频率 C.方差或极差 D.频数或众数
9.一组数据1,2,1,4的方差为( )
A.1 B.1.5 C.2 D.2.5
10.若一列数据x1,x2,x3,…,xn,的平均数是3,方差是2,则数据x1+5,x2+5,…,xn+5的平均数与方差分别是( )
A.8,7 B.5,5 C.3,2 D.8,2
二、填空题
11.质量检测部门对甲、乙两工厂生产的同样产品抽样调查,计算出甲厂的样本方差为0.99,乙厂的样本方差为1.22.由此可以推断出生产此类产品,质量比较稳定的是 厂.
12.若5个正整数从小到大排序,其中中位数是4,如果这组数据的唯一众数是5,当这5个正整数的和为最大值时,这组数据的方差为 .
13.若样本数据3、6、a、4、2的平均数是4,则其方差是
14.已知1,2,3,4,,,的平均数是8,那么的值 .
15.数据﹣4,﹣2,0,2,4的方差是 .
16.已知5筐苹果的质量分别为(单位:kg):52,49,50,53,51,则这5筐苹果的平均质量为 kg.
17.若1、2、3、a的平均数是3,又4、5、a、b的平均数是5,则样本a+b= ,0、1、2、3、4、a、b的平均数是 .
18.一组数据1,1,x,3,4的平均数为3,则x表示的数为 .
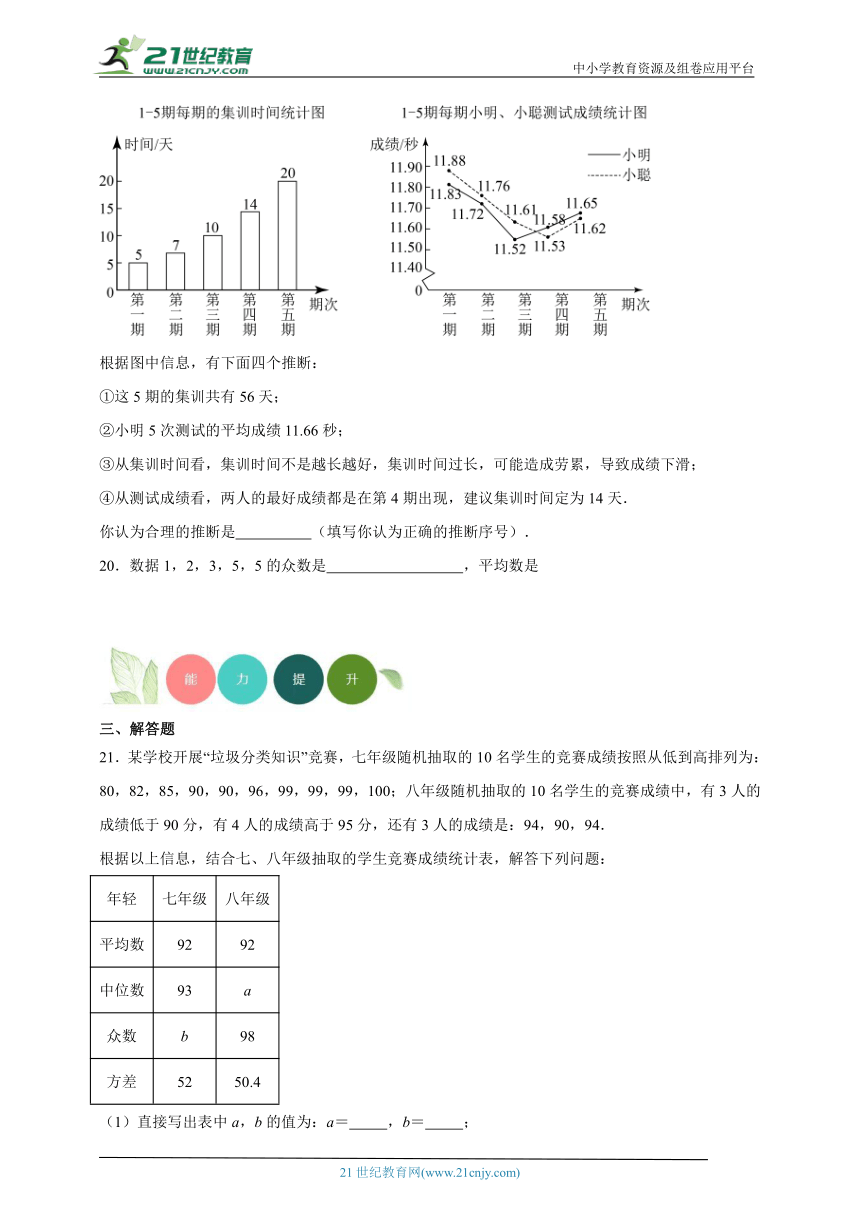
19.小明、小聪参加了跑的5期集训,每期集训结束时进行测试,根据他们的集训时间、测试成绩绘制成如图的两个统计图.
根据图中信息,有下面四个推断:
①这5期的集训共有56天;
②小明5次测试的平均成绩11.66秒;
③从集训时间看,集训时间不是越长越好,集训时间过长,可能造成劳累,导致成绩下滑;
④从测试成绩看,两人的最好成绩都是在第4期出现,建议集训时间定为14天.
你认为合理的推断是 (填写你认为正确的推断序号).
20.数据1,2,3,5,5的众数是 ,平均数是
三、解答题
21.某学校开展“垃圾分类知识”竞赛,七年级随机抽取的10名学生的竞赛成绩按照从低到高排列为:80,82,85,90,90,96,99,99,99,100;八年级随机抽取的10名学生的竞赛成绩中,有3人的成绩低于90分,有4人的成绩高于95分,还有3人的成绩是:94,90,94.
根据以上信息,结合七、八年级抽取的学生竞赛成绩统计表,解答下列问题:
年轻 七年级 八年级
平均数 92 92
中位数 93 a
众数 b 98
方差 52 50.4
(1)直接写出表中a,b的值为:a= ,b= ;
(2)该校七、八年级共200人参加了此次竞赛活动,估计参加此次竞赛活动成绩不低于90分的学生人数是 ;
(3)根据以上数据,你认为该校七、八年级中哪个年级学生掌握垃圾分类知识较好?请说明理由(一条理由即可).
22.2020年6月29日至7月5日是我国第30个全国节能宣传周,主题为“绿水青山,节能增效”.某学校为配合宣传活动,抽查了某班级10天的用电量(单位:度),数据如下表:
度数 8 9 10 13 14 15
天数 1 1 2 3 1 2
(1)这10天用电量的众数是_______度,中位数是_______度;
(2)求这个班级平均每天的用电量.
23.甲、乙两校各组织300名学生参加联赛,为了解两校联赛成绩情况,在两校随机抽取部分学生的联赛成绩,两校抽取的人数相等,结果如下(数据包括左端点不包括右端点).
(1)若小明是乙校的学生,他的成绩是75分,请结合数据分析小明的成绩;
(2)若甲校中一位同学的成绩不纳入计算后,甲校的平均成绩提高了,你认为这位同学的成绩一定不可能在哪个分数段?
(3)请用适当的统计量从两个不同角度分析哪所学校的联赛成绩整体较好?
24.我们约定:如果身高在选定标准的±2%范围之内都称为“普启遍身高”.为了了解某校九年级男生中具有“普遍身高”的人数,我们从该校九年级男生中随机抽出10名男生,分别测量出他们的身高(单位:cm),收集并整理如下统计表:
男生 序号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩
身高x(cm) 163 171 173 159 161 174 164 166 169 164
根据以上信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数、众数;
(2)请你选择其中一个统计量作为选定标准,找出这10名男生中具有“普遍身高”是哪几位男生?并说明理由.
25.在世园会开幕一周年之际,延庆区围绕“践行‘两山’理论,聚力冬奥筹办,建设美丽延庆”主题,同筑生态文明.近年来,在延庆区政府的积极治理下,空气质量得到极大改善.下图是根据延庆区环境保护局公布的2014~2020年各年的全年空气质量优良天数绘制的折线统计图.
请结合统计图解答下列问题:
(1)2020年比2016年的全年空气质量优良天数增加了______天;
(2)这七年的全年空气质量优良天数的中位数是______;
(3)在生态环境部2月25日举行的例行新闻发布会上透露,“十四五”空气质量改善目标指标设置仍然坚持PM和优良天数两个指标;其中,全国优良天数达标指标将提升至%.截止到3月31日,延庆区2021年空气质量优良天数如下:
月份 1月(31天) 2月(28天) 3月(31天)
优良天数/天 28 25 28
①该小区2021年1月1日至3月31日的空气质量优良天数的平均数约为______.
②试根据以上信息预测延庆区2021年(共365天)全年空气质量优良天数能否达标?达标的天数约为多少天?
参考答案:
1.C
2.B
3.D
4.C
5.D
6.C
7.A
8.C
9.B
10.D
11.甲
12.1.36
13.2.
14.46
15.8.
16.51
17. 11 3
18.6
19.①②③
20.5;
21.(1)94,99;(2)140;(3)该校七、八年级中八年级学生掌握垃圾分类知识较好.
22.(1)13,13;(2)10.5度
23.(1)(1)乙校成绩的中位数处于这一组,说明小明的成绩在乙校大致处于中等水平,或乙校成绩的平均数约为6.75分,说明小明的成绩在乙校均水平;(2)不在,这两个分数段内;(3)从平均数看,乙校的平均分75.6分,高于甲校的平均分75分;从中位数看,甲、乙两校的中位数都落在之间;从众数看,甲校的众数落在,乙校的众数落在,所以乙校的联赛成绩整体较好.
24.(1)平均数166.4(cm),中位数 165,众数 164;(2)①⑤⑦⑧⑩男生的身高具有“普遍身高”
25.(1)37天;(2)265天;(3)①27天;②达标;328天.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.1总体平均数与方差的估计
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在测量某物理量的过程中,因为仪器和观察的误差,使得次测量分别得到共个数据,我们规定所测得的物理量的“最佳近似值”是这样一个数据:与其他近似值比较,与各个数据差的平方和最小.若三次测量得到的数据依次为,依据此规定,那么本次测量的“最佳近似值”为( )
A.1.21 B.1.25 C.1.22 D.1.23
2.下列说法正确的是( )
A.的算术平方根是9
B.一组数据的极差、方差或标准差越小,这组数据就越稳定
C.三角形的一个外角等于它的两个内角之和
D.立方根等于自身的数有1和0
3.在一次数学竞赛活动中,五位同学答对题目的个数分别为7,5,3,5,10.则关于这组数据的结论不正确的是( )
A.众数是5 B.平均数是6 C.中位数是5 D.中位数是3
4.在社会实践活动中,某中学对甲、乙、丙、丁四个超市三月份的苹果价格进行调查,它们的价格的平均值均为元,方差分别为,,,.三月份苹果价格最稳定的超市是( )
A.甲 B.乙 C.丙 D.丁
5.数据是某班六位同学定点投篮(每人投10个)的情况,投进篮筐的个数为6,9,8,4,0,3,这组数据的平均数、中位数和极差分别是( )
A.6,6,9 B.6,5,9 C.5,6,6 D.5,5,9
6.若1,2,3,x的平均数是6.且1,2,3,x,y的平均数是7,则y的值为( )
A.7 B.9 C.11 D.13
7.有一句地方民谣“早穿皮袄午穿纱”,说明此地气温的下列特征数中,较大的是( )
A.极差 B.平均数 C.众数 D.中位数
8.教练组对运动员正式比赛前的5次训练成绩进行分析,判断谁的成绩更加稳定,一般需要考察这5次成绩的 ( )
A.平均数或中位数 B.众数或频率 C.方差或极差 D.频数或众数
9.一组数据1,2,1,4的方差为( )
A.1 B.1.5 C.2 D.2.5
10.若一列数据x1,x2,x3,…,xn,的平均数是3,方差是2,则数据x1+5,x2+5,…,xn+5的平均数与方差分别是( )
A.8,7 B.5,5 C.3,2 D.8,2
二、填空题
11.质量检测部门对甲、乙两工厂生产的同样产品抽样调查,计算出甲厂的样本方差为0.99,乙厂的样本方差为1.22.由此可以推断出生产此类产品,质量比较稳定的是 厂.
12.若5个正整数从小到大排序,其中中位数是4,如果这组数据的唯一众数是5,当这5个正整数的和为最大值时,这组数据的方差为 .
13.若样本数据3、6、a、4、2的平均数是4,则其方差是
14.已知1,2,3,4,,,的平均数是8,那么的值 .
15.数据﹣4,﹣2,0,2,4的方差是 .
16.已知5筐苹果的质量分别为(单位:kg):52,49,50,53,51,则这5筐苹果的平均质量为 kg.
17.若1、2、3、a的平均数是3,又4、5、a、b的平均数是5,则样本a+b= ,0、1、2、3、4、a、b的平均数是 .
18.一组数据1,1,x,3,4的平均数为3,则x表示的数为 .
19.小明、小聪参加了跑的5期集训,每期集训结束时进行测试,根据他们的集训时间、测试成绩绘制成如图的两个统计图.
根据图中信息,有下面四个推断:
①这5期的集训共有56天;
②小明5次测试的平均成绩11.66秒;
③从集训时间看,集训时间不是越长越好,集训时间过长,可能造成劳累,导致成绩下滑;
④从测试成绩看,两人的最好成绩都是在第4期出现,建议集训时间定为14天.
你认为合理的推断是 (填写你认为正确的推断序号).
20.数据1,2,3,5,5的众数是 ,平均数是
三、解答题
21.某学校开展“垃圾分类知识”竞赛,七年级随机抽取的10名学生的竞赛成绩按照从低到高排列为:80,82,85,90,90,96,99,99,99,100;八年级随机抽取的10名学生的竞赛成绩中,有3人的成绩低于90分,有4人的成绩高于95分,还有3人的成绩是:94,90,94.
根据以上信息,结合七、八年级抽取的学生竞赛成绩统计表,解答下列问题:
年轻 七年级 八年级
平均数 92 92
中位数 93 a
众数 b 98
方差 52 50.4
(1)直接写出表中a,b的值为:a= ,b= ;
(2)该校七、八年级共200人参加了此次竞赛活动,估计参加此次竞赛活动成绩不低于90分的学生人数是 ;
(3)根据以上数据,你认为该校七、八年级中哪个年级学生掌握垃圾分类知识较好?请说明理由(一条理由即可).
22.2020年6月29日至7月5日是我国第30个全国节能宣传周,主题为“绿水青山,节能增效”.某学校为配合宣传活动,抽查了某班级10天的用电量(单位:度),数据如下表:
度数 8 9 10 13 14 15
天数 1 1 2 3 1 2
(1)这10天用电量的众数是_______度,中位数是_______度;
(2)求这个班级平均每天的用电量.
23.甲、乙两校各组织300名学生参加联赛,为了解两校联赛成绩情况,在两校随机抽取部分学生的联赛成绩,两校抽取的人数相等,结果如下(数据包括左端点不包括右端点).
(1)若小明是乙校的学生,他的成绩是75分,请结合数据分析小明的成绩;
(2)若甲校中一位同学的成绩不纳入计算后,甲校的平均成绩提高了,你认为这位同学的成绩一定不可能在哪个分数段?
(3)请用适当的统计量从两个不同角度分析哪所学校的联赛成绩整体较好?
24.我们约定:如果身高在选定标准的±2%范围之内都称为“普启遍身高”.为了了解某校九年级男生中具有“普遍身高”的人数,我们从该校九年级男生中随机抽出10名男生,分别测量出他们的身高(单位:cm),收集并整理如下统计表:
男生 序号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩
身高x(cm) 163 171 173 159 161 174 164 166 169 164
根据以上信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数、众数;
(2)请你选择其中一个统计量作为选定标准,找出这10名男生中具有“普遍身高”是哪几位男生?并说明理由.
25.在世园会开幕一周年之际,延庆区围绕“践行‘两山’理论,聚力冬奥筹办,建设美丽延庆”主题,同筑生态文明.近年来,在延庆区政府的积极治理下,空气质量得到极大改善.下图是根据延庆区环境保护局公布的2014~2020年各年的全年空气质量优良天数绘制的折线统计图.
请结合统计图解答下列问题:
(1)2020年比2016年的全年空气质量优良天数增加了______天;
(2)这七年的全年空气质量优良天数的中位数是______;
(3)在生态环境部2月25日举行的例行新闻发布会上透露,“十四五”空气质量改善目标指标设置仍然坚持PM和优良天数两个指标;其中,全国优良天数达标指标将提升至%.截止到3月31日,延庆区2021年空气质量优良天数如下:
月份 1月(31天) 2月(28天) 3月(31天)
优良天数/天 28 25 28
①该小区2021年1月1日至3月31日的空气质量优良天数的平均数约为______.
②试根据以上信息预测延庆区2021年(共365天)全年空气质量优良天数能否达标?达标的天数约为多少天?
参考答案:
1.C
2.B
3.D
4.C
5.D
6.C
7.A
8.C
9.B
10.D
11.甲
12.1.36
13.2.
14.46
15.8.
16.51
17. 11 3
18.6
19.①②③
20.5;
21.(1)94,99;(2)140;(3)该校七、八年级中八年级学生掌握垃圾分类知识较好.
22.(1)13,13;(2)10.5度
23.(1)(1)乙校成绩的中位数处于这一组,说明小明的成绩在乙校大致处于中等水平,或乙校成绩的平均数约为6.75分,说明小明的成绩在乙校均水平;(2)不在,这两个分数段内;(3)从平均数看,乙校的平均分75.6分,高于甲校的平均分75分;从中位数看,甲、乙两校的中位数都落在之间;从众数看,甲校的众数落在,乙校的众数落在,所以乙校的联赛成绩整体较好.
24.(1)平均数166.4(cm),中位数 165,众数 164;(2)①⑤⑦⑧⑩男生的身高具有“普遍身高”
25.(1)37天;(2)265天;(3)①27天;②达标;328天.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
