第二章 机械振动单元复习课件(共26张PPT)高二物理(人教版2019选择性必修第一册)(26张ppt)
文档属性
| 名称 | 第二章 机械振动单元复习课件(共26张PPT)高二物理(人教版2019选择性必修第一册)(26张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-13 10:11:58 | ||
图片预览








文档简介
(共26张PPT)
第二章 机械振动
(复习与提升)
01
02
重点突破
知识清单
目录
第一部分:知识清单
钟摆来回摆动
一、简谐运动及其描述
简
谐
运
动
二、两个重要模型
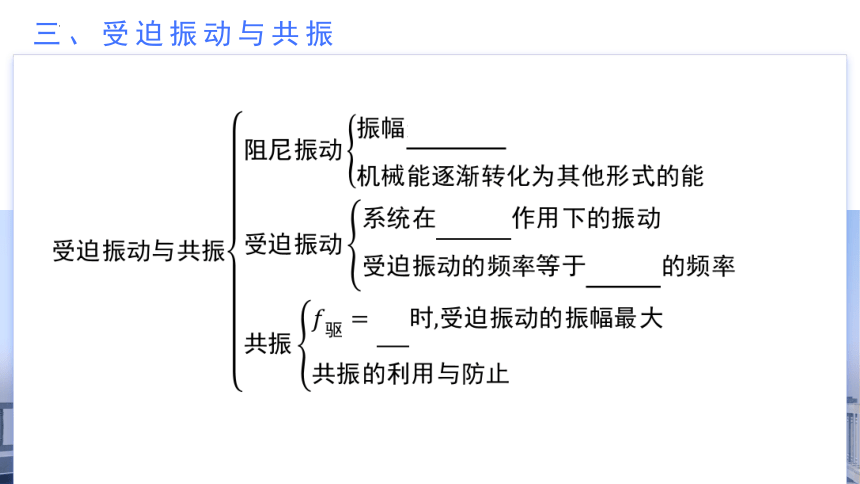
三、受迫振动与共振
第二部分:重点突破
钟摆来回摆动
一、简谐运动的图像及其应用
1.对简谐运动图像的认识
(1)简谐运动的图像是一条正弦曲线,如图所示。
(2)图像反映了质点的位移随时间变化的规律,不代表质点运动的轨迹。
2.图像信息
(1)由图像可以得出质点做简谐运动的振幅、周期和频率。
(2)可以确定某时刻质点离开平衡位置的位移。
(3)可以确定某时刻质点回复力、加速度的方向。因回复力总是指向平衡位置,故回复力和加速度的方向在图像上总是指向t轴。
(4)确定某时刻质点速度的方向。速度的方向可以通过下一时刻位移的变化来判定,若下一时刻位移增加,振动质点的速度方向就是远离t轴,若下一时刻位移减小,振动质点的速度方向就是指向t轴。
(5)比较不同时刻回复力、加速度的大小。
(6)比较不同时刻质点的动能、势能的大小。
一、简谐运动的图像及其应用
【例1】 如图所示是一个质点做简谐运动的图像,根据图像回答下面的问题:
一、简谐运动的图像及其应用
(1)振动质点离开平衡位置的最大距离;
【解析】 由振动图像可以看出,质点振动的振幅为,即此质点离开平衡位置的最大距离
(2) 写出此振动质点的运动表达式;
【解析】 由质点的振动图像可知
,,,所以
【例1】 如图所示是一个质点做简谐运动的图像,根据图像回答下面的问题:
一、简谐运动的图像及其应用
(3) 振动质点在0~0.6 s的时间内通过的路程;
【解析】由振动图像可以看出,质点振动的周期为,,质点是从平衡位置开始振动的,故在0~0.6 s的时间内质点通过的路程为。
【例1】 如图所示是一个质点做简谐运动的图像,根据图像回答下面的问题:
一、简谐运动的图像及其应用
(4) 振动质点在t=0.1 s、0.3 s、0.5 s、0.7 s时的振动方向;
【解析】在时,振动质点处在位移为正值的某一位置上,但若从起取一段极短的时间间隔的话,从图像中可以看出质点的正方向的位移将会增大,由此可以判断得出质点在时的振动方向是沿题中所设的正方向。同理可以判断得出质点在、、时的振动方向分别是沿题中所设的负方向、负方向和正方向。
【例1】 如图所示是一个质点做简谐运动的图像,根据图像回答下面的问题:
一、简谐运动的图像及其应用
(5) 振动质点在0.6~0.8 s这段时间内速度和加速度是怎样变化的?
【解析】 由振动图像可以看出,在0.6~0.8 s这段时间内,质点从负的最大位移处向平衡位置运动,故其速度是越来越大的;而质点所受的回复力是指向平衡位置的,并且逐渐减小,故其加速度的方向指向平衡位置且越来越小。
【例1】 如图所示是一个质点做简谐运动的图像,根据图像回答下面的问题:
一、简谐运动的图像及其应用
(6) 振动质点在0.4~0.8 s这段时间内的动能变化是多少?
【解析】由图像可看出,在0.4~0.8 s这段时间内质点从平衡位置经过半个周期的运动又回到了平衡位置,尽管初、末两个时刻的速度方向相反,但大小是相等的,故这段时间内质点的动能变化为零。
【典例2】图(a)、(b)分别是甲、乙两个单摆在同一位置处做简谐运动的图像,则下列说法中正确的是 ( )
A.甲、乙两单摆的振幅相等
B.t=2 s时,甲单摆的重力势能最小,乙单摆的动能为零
C.甲、乙两单摆的摆长之比为4∶1
D.甲、乙两单摆的摆球在最低点时,向心加速度大小一定相等
一、简谐运动的图像及其应用
一、简谐运动的图像及其应用
【答案】B
二、简谐运动的周期性和对称性
1.周期性
做简谐运动的物体在完成一次全振动后,再次振动时则是重复上一个振动的形式,所以简谐运动具有周期性,因此在处理实际问题时,要注意多解的可能性。
2.对称性
简谐运动过程具有对称性,关于平衡位置对称的两位置上速度、加速度、回复力、位移、动能、势能的大小均相等,且由某点到平衡位置和由平衡位置到该点或对称点的时间相等,由某点到最大位移处和由最大位移处回到该点的时间相等。
二、简谐运动的周期性和对称性
【典例3】弹簧振子以点为平衡位置,在、两点间做简谐运动,在时刻,从、间的点以速度向点运动;在时,振子速度第一次变为;再经过0.30 s时,振子速度第二次变为。
(1) 求弹簧振子振动的周期T;
【解析]】由题意结合简谐运动的对称性知,0.20 s内,振子从点运动到点,又从点第一次回到点,再经0.30 s振子从点经点第一次运动到点关于点的对称点,如图所示。由图可以看出,,。则,所以。
二、简谐运动的周期性和对称性
【典例3】弹簧振子以点为平衡位置,在、两点间做简谐运动,在时刻,从、间的点以速度向点运动;在时,振子速度第一次变为;再经过0.30 s时,振子速度第二次变为。
(2) 若B、C之间的距离为25 cm,求振子在4.0 s内通过的路程。
【解析】振子的振幅,因,所以振子通过的路程。
二、简谐运动的周期性和对称性
【典例4】如图所示,一个做简谐运动的质点,先后以同样大小的速度通过相距10 cm的A、B两点,历时0.5 s,过B点后再经过t=0.5 s质点以方向相反、大小相同的速度再次通过B点,则质点振动的周期是( )
A.0.5 s B.1.0 s
C.2.0 s D.4.0 s
【答案】C
【解析】如图所示,设C、D为质点振动中左方和右方的极端位置,则由对称性可知,质点从B→D→B的时间一定等于质点从A→C→A的时间,即tBDB=tACA=0.5 s。所以,质点振动周期T=tAB+tBDB+tBA+tACA=2 s,故C正确。
三、简谐运动的两种模型
模型 弹簧振子(水平) 单摆
示意图
简谐运动条件 ①弹簧质量要忽略 ②无摩擦等阻力 ③在弹簧弹性限度内 ①摆线为不可伸缩的轻细线
②无空气阻力等
③最大摆角小于等于5°
三、简谐运动的两种模型
回复力 弹簧的弹力提供 摆球重力沿与摆线垂直方向(即切向)的分力
平衡位置 弹簧处于原长处 最低点
周期 与振幅无关 T=2π
能量转化 弹性势能与动能的相互转化,机械能守恒 重力势能与动能的相互转化,机械能守恒
续表
三、简谐运动的两种模型
【典例5】图(a)、(b)分别是甲、乙两个单摆在同一位置处做简谐运动的图像,则下列说法中正确的是 ( )
A.甲、乙两单摆的振幅相等
B.t=2 s时,甲单摆的重力势能最小,乙单摆的动能为零
C.甲、乙两单摆的摆长之比为4∶1
D.甲、乙两单摆的摆球在最低点时,向心加速度大小一定相等
三、简谐运动的两种模型
【答案】 B
三、简谐运动的两种模型
三、简谐运动的两种模型
第二章 机械振动
(复习与提升)
01
02
重点突破
知识清单
目录
第一部分:知识清单
钟摆来回摆动
一、简谐运动及其描述
简
谐
运
动
二、两个重要模型
三、受迫振动与共振
第二部分:重点突破
钟摆来回摆动
一、简谐运动的图像及其应用
1.对简谐运动图像的认识
(1)简谐运动的图像是一条正弦曲线,如图所示。
(2)图像反映了质点的位移随时间变化的规律,不代表质点运动的轨迹。
2.图像信息
(1)由图像可以得出质点做简谐运动的振幅、周期和频率。
(2)可以确定某时刻质点离开平衡位置的位移。
(3)可以确定某时刻质点回复力、加速度的方向。因回复力总是指向平衡位置,故回复力和加速度的方向在图像上总是指向t轴。
(4)确定某时刻质点速度的方向。速度的方向可以通过下一时刻位移的变化来判定,若下一时刻位移增加,振动质点的速度方向就是远离t轴,若下一时刻位移减小,振动质点的速度方向就是指向t轴。
(5)比较不同时刻回复力、加速度的大小。
(6)比较不同时刻质点的动能、势能的大小。
一、简谐运动的图像及其应用
【例1】 如图所示是一个质点做简谐运动的图像,根据图像回答下面的问题:
一、简谐运动的图像及其应用
(1)振动质点离开平衡位置的最大距离;
【解析】 由振动图像可以看出,质点振动的振幅为,即此质点离开平衡位置的最大距离
(2) 写出此振动质点的运动表达式;
【解析】 由质点的振动图像可知
,,,所以
【例1】 如图所示是一个质点做简谐运动的图像,根据图像回答下面的问题:
一、简谐运动的图像及其应用
(3) 振动质点在0~0.6 s的时间内通过的路程;
【解析】由振动图像可以看出,质点振动的周期为,,质点是从平衡位置开始振动的,故在0~0.6 s的时间内质点通过的路程为。
【例1】 如图所示是一个质点做简谐运动的图像,根据图像回答下面的问题:
一、简谐运动的图像及其应用
(4) 振动质点在t=0.1 s、0.3 s、0.5 s、0.7 s时的振动方向;
【解析】在时,振动质点处在位移为正值的某一位置上,但若从起取一段极短的时间间隔的话,从图像中可以看出质点的正方向的位移将会增大,由此可以判断得出质点在时的振动方向是沿题中所设的正方向。同理可以判断得出质点在、、时的振动方向分别是沿题中所设的负方向、负方向和正方向。
【例1】 如图所示是一个质点做简谐运动的图像,根据图像回答下面的问题:
一、简谐运动的图像及其应用
(5) 振动质点在0.6~0.8 s这段时间内速度和加速度是怎样变化的?
【解析】 由振动图像可以看出,在0.6~0.8 s这段时间内,质点从负的最大位移处向平衡位置运动,故其速度是越来越大的;而质点所受的回复力是指向平衡位置的,并且逐渐减小,故其加速度的方向指向平衡位置且越来越小。
【例1】 如图所示是一个质点做简谐运动的图像,根据图像回答下面的问题:
一、简谐运动的图像及其应用
(6) 振动质点在0.4~0.8 s这段时间内的动能变化是多少?
【解析】由图像可看出,在0.4~0.8 s这段时间内质点从平衡位置经过半个周期的运动又回到了平衡位置,尽管初、末两个时刻的速度方向相反,但大小是相等的,故这段时间内质点的动能变化为零。
【典例2】图(a)、(b)分别是甲、乙两个单摆在同一位置处做简谐运动的图像,则下列说法中正确的是 ( )
A.甲、乙两单摆的振幅相等
B.t=2 s时,甲单摆的重力势能最小,乙单摆的动能为零
C.甲、乙两单摆的摆长之比为4∶1
D.甲、乙两单摆的摆球在最低点时,向心加速度大小一定相等
一、简谐运动的图像及其应用
一、简谐运动的图像及其应用
【答案】B
二、简谐运动的周期性和对称性
1.周期性
做简谐运动的物体在完成一次全振动后,再次振动时则是重复上一个振动的形式,所以简谐运动具有周期性,因此在处理实际问题时,要注意多解的可能性。
2.对称性
简谐运动过程具有对称性,关于平衡位置对称的两位置上速度、加速度、回复力、位移、动能、势能的大小均相等,且由某点到平衡位置和由平衡位置到该点或对称点的时间相等,由某点到最大位移处和由最大位移处回到该点的时间相等。
二、简谐运动的周期性和对称性
【典例3】弹簧振子以点为平衡位置,在、两点间做简谐运动,在时刻,从、间的点以速度向点运动;在时,振子速度第一次变为;再经过0.30 s时,振子速度第二次变为。
(1) 求弹簧振子振动的周期T;
【解析]】由题意结合简谐运动的对称性知,0.20 s内,振子从点运动到点,又从点第一次回到点,再经0.30 s振子从点经点第一次运动到点关于点的对称点,如图所示。由图可以看出,,。则,所以。
二、简谐运动的周期性和对称性
【典例3】弹簧振子以点为平衡位置,在、两点间做简谐运动,在时刻,从、间的点以速度向点运动;在时,振子速度第一次变为;再经过0.30 s时,振子速度第二次变为。
(2) 若B、C之间的距离为25 cm,求振子在4.0 s内通过的路程。
【解析】振子的振幅,因,所以振子通过的路程。
二、简谐运动的周期性和对称性
【典例4】如图所示,一个做简谐运动的质点,先后以同样大小的速度通过相距10 cm的A、B两点,历时0.5 s,过B点后再经过t=0.5 s质点以方向相反、大小相同的速度再次通过B点,则质点振动的周期是( )
A.0.5 s B.1.0 s
C.2.0 s D.4.0 s
【答案】C
【解析】如图所示,设C、D为质点振动中左方和右方的极端位置,则由对称性可知,质点从B→D→B的时间一定等于质点从A→C→A的时间,即tBDB=tACA=0.5 s。所以,质点振动周期T=tAB+tBDB+tBA+tACA=2 s,故C正确。
三、简谐运动的两种模型
模型 弹簧振子(水平) 单摆
示意图
简谐运动条件 ①弹簧质量要忽略 ②无摩擦等阻力 ③在弹簧弹性限度内 ①摆线为不可伸缩的轻细线
②无空气阻力等
③最大摆角小于等于5°
三、简谐运动的两种模型
回复力 弹簧的弹力提供 摆球重力沿与摆线垂直方向(即切向)的分力
平衡位置 弹簧处于原长处 最低点
周期 与振幅无关 T=2π
能量转化 弹性势能与动能的相互转化,机械能守恒 重力势能与动能的相互转化,机械能守恒
续表
三、简谐运动的两种模型
【典例5】图(a)、(b)分别是甲、乙两个单摆在同一位置处做简谐运动的图像,则下列说法中正确的是 ( )
A.甲、乙两单摆的振幅相等
B.t=2 s时,甲单摆的重力势能最小,乙单摆的动能为零
C.甲、乙两单摆的摆长之比为4∶1
D.甲、乙两单摆的摆球在最低点时,向心加速度大小一定相等
三、简谐运动的两种模型
【答案】 B
三、简谐运动的两种模型
三、简谐运动的两种模型
