幂函数(1)

课件17张PPT。2.3 幂函数我们先看下面几个具体问题：如果正方形的边长为a，那么正方形的面积s (2) 如果立方体的边长为a，那么立方体的体积v(3) 如果一个正方形场地的面积为S，那么这个 正方形的边长aS=a2，这里S是a的函数；V=a3，这里V是a的函数；(4) 如果某人t s内骑车行进了１km，那么他骑车的平均速度v,这里a是S的函数； km/s,这里v是t的函数.
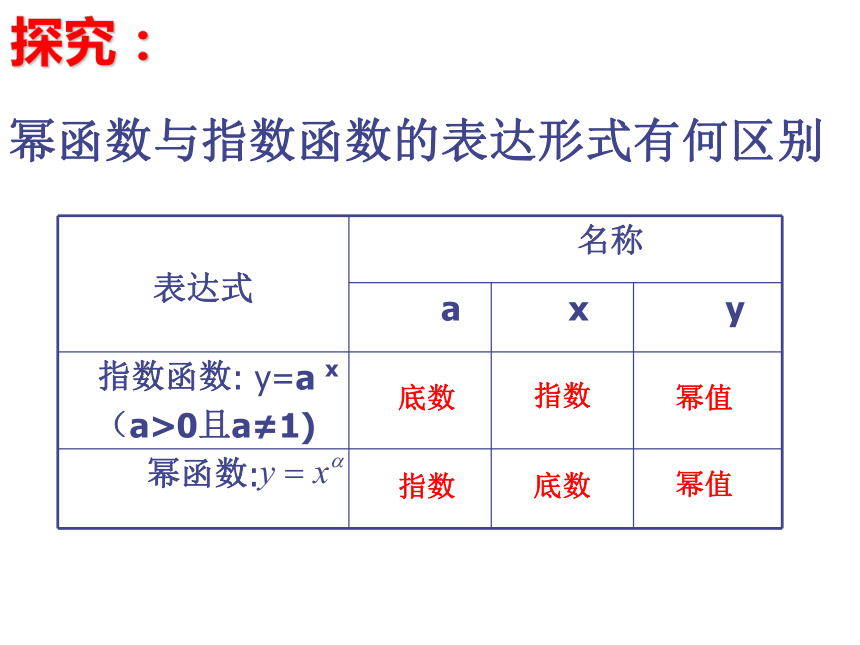
它们有以下共同特点：(1)都是函数；(3) 均是以自变量为底的幂；(2) 指数为常数. 一般地，函数y=xα叫做幂函数，其中x是自变量，α是常数.幂函数中α可以为任意实数.注意:底数
指数指数
底数
幂值幂值探究： 幂函数与指数函数的表达形式有何区别例1:判断下列函数是否为幂函数.归纳：根据幂函数的定义判断．变式：练习3、已知 是幂函数，求m，n的值 例2：写出下列函数的定义域，并分别指出它们的奇偶性。（1）
(2）
R奇函数非奇非偶函数 1、定义域指使函数表达式有意义的x的集合 归纳 2、奇偶性根据定义得出结论作出下列函数的图象:（3）(-∞,0)减(-∞,0]减(1,1)(1,1)(1,1)(1,1)(1,1)公共点(0,+∞)减增增[0,+∞)增增单调性奇非奇非偶奇偶奇奇偶性[0,+∞)R[0,+∞)R值域[0,+∞)ＲＲＲ定义域y=x-1y=x3y=x2y=x 函数
性质幂函数的性质　(1)幂函数的图象都通过点(2) 如果α＞０，
在 区间[0,+∞)上是 如果a＜０，
在区间(0,+∞)上是 当α为偶数时，
幂函数为幂函数的性质增函数减函数(3) 当α为奇数时，
幂函数为偶函数奇函数；(1,1)例3　比较下列各组数的大小；利用幂函数的增减性比较两个数的大小.注意:当不能直接进行比较时,可在两个数中间
插入一个中间数,间接比较上述两个数的大小例4.证明幂函数 在[0,+∞)上是增函数．证明：任取x1,x2∈ [0,+∞)，且x1＜x2，则小结(1) 幂函数的定义；(2) 幂函数的性质；(3) 利用幂函数的单调性判别大小 一般地，函数y=xα叫做幂函数，其中x是自变量，α是常数.作业课本P79 习题第3题
课本P82 第10题拓展探索