18.1勾股定理课件
图片预览








文档简介
课件45张PPT。勾股定理 受台风麦莎影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
毕达哥拉斯
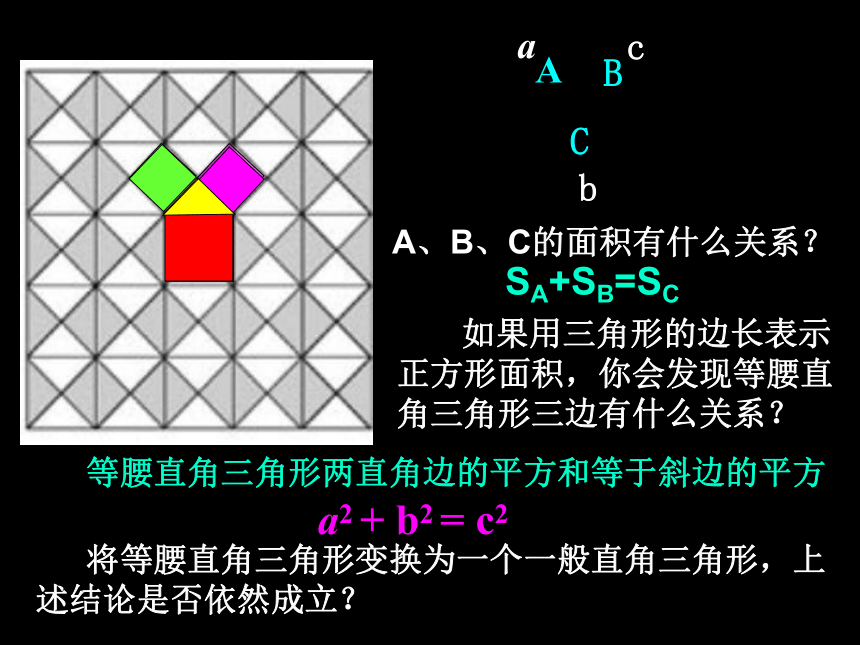
(公元前572----前492年),古希腊著名的哲学家、数学家、天文学家。情境再现 相传2500年前,一次,毕达哥拉斯去朋友家作客.在宴席上他看着朋友家的方砖地面发起呆来.主人觉得非常奇怪,就想过去问他.谁知毕达哥拉斯突然恍然大悟的样子,站起来,大笑着跑回家去了.后来知道是因为他从中发现了直角三角形三边的数量关系,赶着回家证明去了。 那么,他朋友家的地板到底是怎样呢?我们也观察一下看看能发现什么?A、B、C的面积有什么关系? 如果用三角形的边长表示正方形面积,你会发现等腰直角三角形三边有什么关系?SA+SB=SC 等腰直角三角形两直角边的平方和等于斜边的平方 将等腰直角三角形变换为一个一般直角三角形,上述结论是否依然成立? a2 + b2 = c2ABC图1图2491392534sA+sB=sC两直角边的平方和
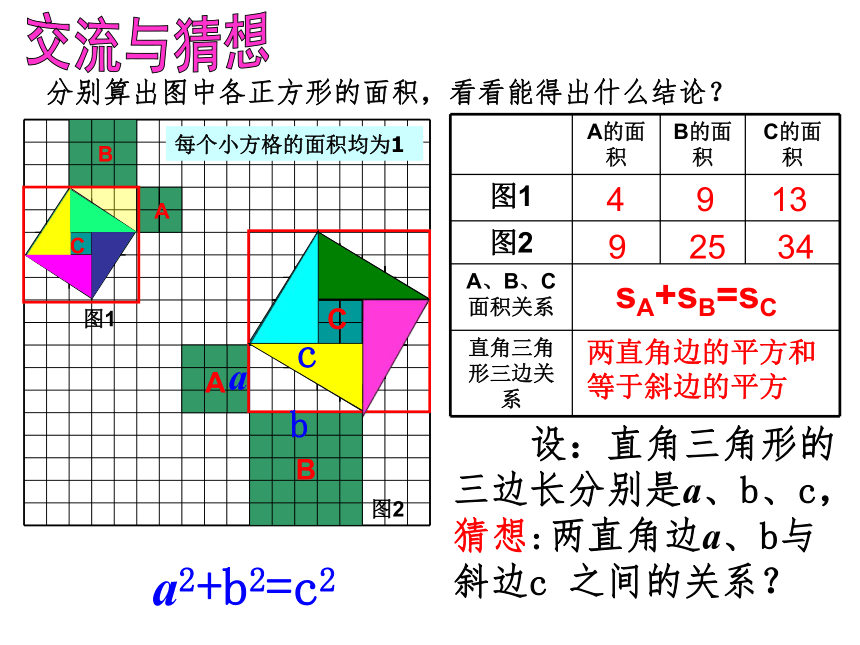
等于斜边的平方分别算出图中各正方形的面积,看看能得出什么结论?交流与猜想 设:直角三角形的三边长分别是a、b、c,猜想:两直角边a、b与斜边c 之间的关系?aba2+b2=c2每个小方格的面积均为1cbCa合作探究 利用准备好的四个全等的直角三角形,a、b表示两条直角边, c表示斜边。动手实践:这四个全等的直角三角形可以拼成一个正方形吗?有些什么不同的方法? 思考:拼出的正方形面积用含a、b、c的式子可以怎么表示?
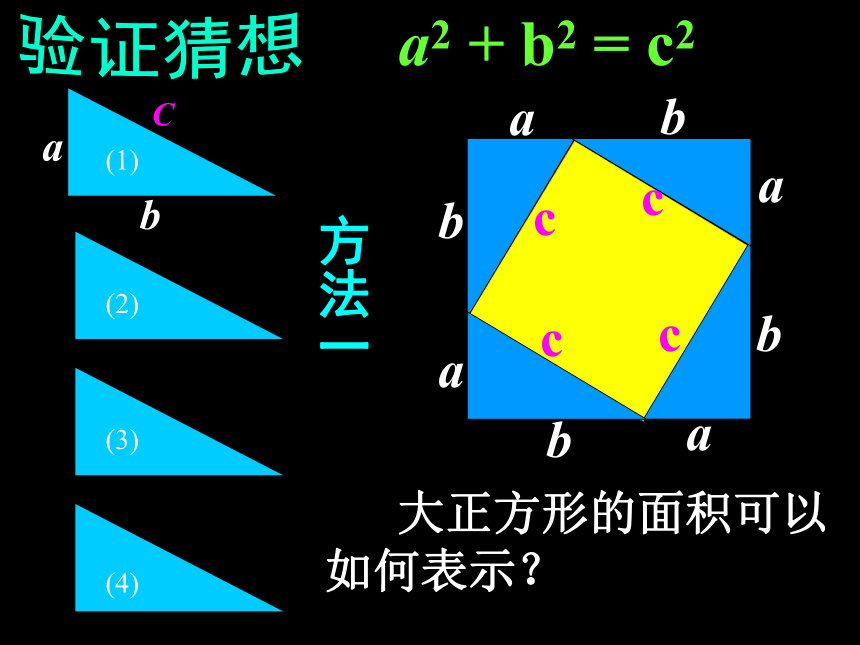
能得到我们要证明的结论吗?方法一验证猜想a2 + b2 = c2bCa 大正方形的面积可以如何表示?
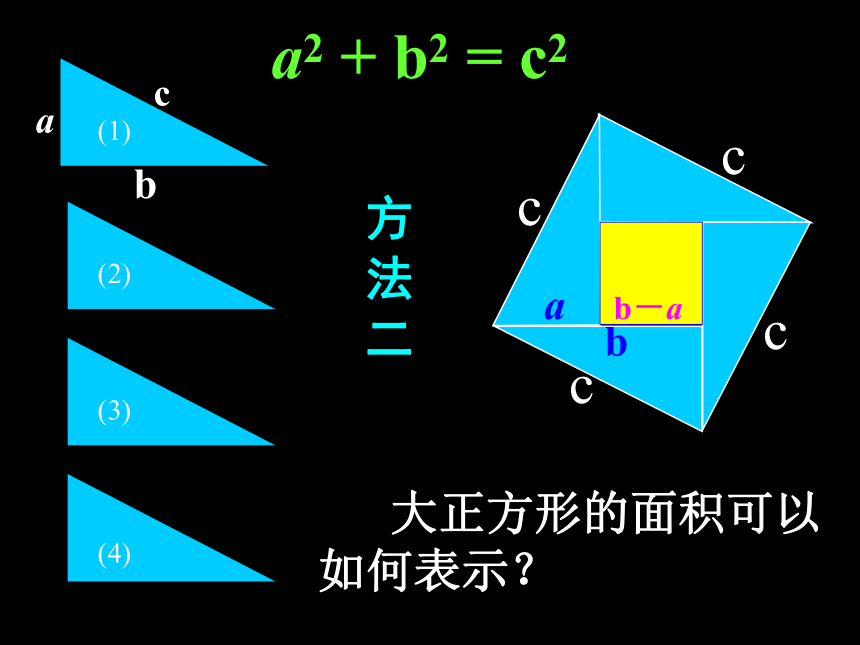
b-a方 法 二aabca2 + b2 = c2b 大正方形的面积可以如何表示? 这个图案公元 3 世纪我国汉代的赵爽在注解《周髀算经》时就已经给出,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形 (黄色).史话弦图赵爽弦图有趣的总统证法:
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 a2 + b2 = c2 在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.勾股定理 如果直角三角形两直角边分别为a、b,斜边为c,那么 即:直角三角形两直角边的平方和等于斜边的平方。a2 + b2 = c2 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方cba公式变形c2=a2 + b2a2=c2-b2b2 =c2-a2 受台风麦莎影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?学以致用 已知直角三角形任意两边求第三边学以致用勾股定理有什么作用呢?一定要在直角三角形中哦! 1.在△ABC中, ∠C=90°,a =6,c=10,
则b=______8牛刀小试2、 ΔABC中,∠C=90o
①若a=3cm, b=4cm,则c= ____cm
②若a=12cm, c=13cm,则b= __ cm
③若c=17cm, a =8cm,则b= __ cm5515 1、 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系. 2、勾股定理: 直角三角形两直角边a、b的平方和, 等于斜边c的平方: 。 3、勾股定理的主要作用是 :在直角三角形中,已知任意两边求第三边的长。 4、我们利用“面积法”证明勾股定理,这体现了数学中数形结合的思想。判断题:
①直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a2+b2 =c2 ( ) . .
②直角三角形的两边长分别是3和4,则第三边长是5. ( )
××能力比拼1、如图已知a=3,b=4
求c=?2、如图已知: c =10,a=6,
求b=?3、如图已知: c =13,a=5,
求阴影部分面积?运用勾股定理时应注意:
⑴在直角三角形中,认准直角边和斜边;
⑵两直角边的平方和等于斜边的平方。4、在? ABC中, ∠ C=90°,若AC=6,CB=8,则?ABC面积为____,斜边为上的高为_____.244.815120 小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错想一想荧屏对角线大约为74厘米勾股定理在实际生活中的应用即 742 = 54763 1、如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了____步路, 却踩伤了花草。 (假设1米为2步)
勾股定理在实际生活中的应用45ABC“路”4 2、如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?8mBCA6m解:根据勾股定理得:
AC2= 62 + 82
=36+64
=100
即:AC=10(不合题意,舍去)
答:梯子至少长10米。 古代笑话一则 有一人拿着一根杆子进屋门,横着拿,不能进,竖着拿,也不能进,干脆将其折断,才解决了问题。请问同学们这样是真正解决了问题了吗?让你做的话,你感觉怎么办合适? 一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?2mDCAB1mcbac2=a2 + b2a2=c2-b2b2 =c2-a2勾股定理:直角三角形两直角边的平方和等于斜边的平方.
1.一个直角三角形的两边长分别为3和4,则第三边长为_______.
2.直角三角形一直角边长为6cm,斜边长为10cm,则这个直角三角形的面积为____,斜边上的高为_______.
3.等腰△ABC的腰长为10cm,底边长为16cm,则底边上的高为____,面积为____________.
5.等腰直角△ABC中,∠C=90°,AC=2cm,那么它的斜边上的高为______.6cmcm 练一练 一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?ACOBD 一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?ACOBD 一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?ACOBD 从题目和图形中,你能得到哪些信息?分析: DB=OD-OB
求BD,可以先求OB、OD. 阿满想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来旗杆的高度吗? ABC5米(x+1)米x米 如图,某公园有这样两棵树,一棵树高8m,另一棵树高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 多少米? 8m2m8m试一试: 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?DABC解:设水池的水深AC为x尺,则这根芦苇长AD =AB =(x+1)尺,在直角三角形ABC中,BC=5尺由勾股定理得:BC2+AC2=AB2即 52 + x2 = (x+1)225 + x2 = x2 +2x + 12x = 24∴ x =12, x+1=13答:水池的水深12尺,这根芦苇长13尺。ADCBDBA说明:在直角三角形中,利用勾股定理计算线段的长,是勾股定理的一个重要的应用.在有直角三角形时,可直接应用;在没有直角三角形时,常作垂线构造直角三角形,为能应用勾股定理创造重要条件. 如图,在△ABC中,AB=15,BC=14,AC=13.求S△ABCCADB 如图,已知:在△ABC中,∠A=90°,AB=AC,CD=CA,DE⊥BC于D,交AB于E,DE=1,求△ABC的周长.ECA111 如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?C解:连结BE∵ DE是AB的中垂线
∴ AE=BE 在Rt△ABC 中
根据勾股定理:设AE = x,则EC=(10-x)BE2=BC2+EC2x2=62+ (10-x)2解得 x = 6.8∴EC=10-6.8=3.2cm折叠问题: 如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕,若AB=9,BC=3,求FC的长?解:由已知AF=FC设AF=x,则FB = 9-x 在R t △FBC中,根据勾股定理:
FC2=FB2+BC2即 x2=(9-x)2+32解得 x=5
即 FC=5折叠问题:D′ x 矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕EF的长。ABCDFEx1010864(8-x)折叠问题:设EF = x 如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长是多少米?183024 在一棵树的10米高的D处有两只猴子,其中一只猴子爬下树走到离树20米的池塘A处,另一只爬到树顶后直接跃向池塘A处,如果两只猴子所经过的直线距离相等,试问这棵树有多高?DABC10米20米┏x 2、在直角三角形中,只知道一边的长度,另外两边只知道它们的关系时,运用勾股定理列方程方法求解。应用勾股定理解决实际问题的一般思路:方程思想是解决数学问题常用的重要思想 1、在解决实际问题时,首先要画出适当的示意图,将实际问题抽象为数学问题,并构建直角三角形模型,再运用勾股定理解决实际问题。感悟与收获请谈谈你的收获……作业:习题18 1第6 8 10 11 12
毕达哥拉斯
(公元前572----前492年),古希腊著名的哲学家、数学家、天文学家。情境再现 相传2500年前,一次,毕达哥拉斯去朋友家作客.在宴席上他看着朋友家的方砖地面发起呆来.主人觉得非常奇怪,就想过去问他.谁知毕达哥拉斯突然恍然大悟的样子,站起来,大笑着跑回家去了.后来知道是因为他从中发现了直角三角形三边的数量关系,赶着回家证明去了。 那么,他朋友家的地板到底是怎样呢?我们也观察一下看看能发现什么?A、B、C的面积有什么关系? 如果用三角形的边长表示正方形面积,你会发现等腰直角三角形三边有什么关系?SA+SB=SC 等腰直角三角形两直角边的平方和等于斜边的平方 将等腰直角三角形变换为一个一般直角三角形,上述结论是否依然成立? a2 + b2 = c2ABC图1图2491392534sA+sB=sC两直角边的平方和
等于斜边的平方分别算出图中各正方形的面积,看看能得出什么结论?交流与猜想 设:直角三角形的三边长分别是a、b、c,猜想:两直角边a、b与斜边c 之间的关系?aba2+b2=c2每个小方格的面积均为1cbCa合作探究 利用准备好的四个全等的直角三角形,a、b表示两条直角边, c表示斜边。动手实践:这四个全等的直角三角形可以拼成一个正方形吗?有些什么不同的方法? 思考:拼出的正方形面积用含a、b、c的式子可以怎么表示?
能得到我们要证明的结论吗?方法一验证猜想a2 + b2 = c2bCa 大正方形的面积可以如何表示?
b-a方 法 二aabca2 + b2 = c2b 大正方形的面积可以如何表示? 这个图案公元 3 世纪我国汉代的赵爽在注解《周髀算经》时就已经给出,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形 (黄色).史话弦图赵爽弦图有趣的总统证法:
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 a2 + b2 = c2 在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.勾股定理 如果直角三角形两直角边分别为a、b,斜边为c,那么 即:直角三角形两直角边的平方和等于斜边的平方。a2 + b2 = c2 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方cba公式变形c2=a2 + b2a2=c2-b2b2 =c2-a2 受台风麦莎影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?学以致用 已知直角三角形任意两边求第三边学以致用勾股定理有什么作用呢?一定要在直角三角形中哦! 1.在△ABC中, ∠C=90°,a =6,c=10,
则b=______8牛刀小试2、 ΔABC中,∠C=90o
①若a=3cm, b=4cm,则c= ____cm
②若a=12cm, c=13cm,则b= __ cm
③若c=17cm, a =8cm,则b= __ cm5515 1、 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系. 2、勾股定理: 直角三角形两直角边a、b的平方和, 等于斜边c的平方: 。 3、勾股定理的主要作用是 :在直角三角形中,已知任意两边求第三边的长。 4、我们利用“面积法”证明勾股定理,这体现了数学中数形结合的思想。判断题:
①直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a2+b2 =c2 ( ) . .
②直角三角形的两边长分别是3和4,则第三边长是5. ( )
××能力比拼1、如图已知a=3,b=4
求c=?2、如图已知: c =10,a=6,
求b=?3、如图已知: c =13,a=5,
求阴影部分面积?运用勾股定理时应注意:
⑴在直角三角形中,认准直角边和斜边;
⑵两直角边的平方和等于斜边的平方。4、在? ABC中, ∠ C=90°,若AC=6,CB=8,则?ABC面积为____,斜边为上的高为_____.244.815120 小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错想一想荧屏对角线大约为74厘米勾股定理在实际生活中的应用即 742 = 54763 1、如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了____步路, 却踩伤了花草。 (假设1米为2步)
勾股定理在实际生活中的应用45ABC“路”4 2、如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?8mBCA6m解:根据勾股定理得:
AC2= 62 + 82
=36+64
=100
即:AC=10(不合题意,舍去)
答:梯子至少长10米。 古代笑话一则 有一人拿着一根杆子进屋门,横着拿,不能进,竖着拿,也不能进,干脆将其折断,才解决了问题。请问同学们这样是真正解决了问题了吗?让你做的话,你感觉怎么办合适? 一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?2mDCAB1mcbac2=a2 + b2a2=c2-b2b2 =c2-a2勾股定理:直角三角形两直角边的平方和等于斜边的平方.
1.一个直角三角形的两边长分别为3和4,则第三边长为_______.
2.直角三角形一直角边长为6cm,斜边长为10cm,则这个直角三角形的面积为____,斜边上的高为_______.
3.等腰△ABC的腰长为10cm,底边长为16cm,则底边上的高为____,面积为____________.
5.等腰直角△ABC中,∠C=90°,AC=2cm,那么它的斜边上的高为______.6cmcm 练一练 一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?ACOBD 一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?ACOBD 一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?ACOBD 从题目和图形中,你能得到哪些信息?分析: DB=OD-OB
求BD,可以先求OB、OD. 阿满想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来旗杆的高度吗? ABC5米(x+1)米x米 如图,某公园有这样两棵树,一棵树高8m,另一棵树高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 多少米? 8m2m8m试一试: 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?DABC解:设水池的水深AC为x尺,则这根芦苇长AD =AB =(x+1)尺,在直角三角形ABC中,BC=5尺由勾股定理得:BC2+AC2=AB2即 52 + x2 = (x+1)225 + x2 = x2 +2x + 12x = 24∴ x =12, x+1=13答:水池的水深12尺,这根芦苇长13尺。ADCBDBA说明:在直角三角形中,利用勾股定理计算线段的长,是勾股定理的一个重要的应用.在有直角三角形时,可直接应用;在没有直角三角形时,常作垂线构造直角三角形,为能应用勾股定理创造重要条件. 如图,在△ABC中,AB=15,BC=14,AC=13.求S△ABCCADB 如图,已知:在△ABC中,∠A=90°,AB=AC,CD=CA,DE⊥BC于D,交AB于E,DE=1,求△ABC的周长.ECA111 如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?C解:连结BE∵ DE是AB的中垂线
∴ AE=BE 在Rt△ABC 中
根据勾股定理:设AE = x,则EC=(10-x)BE2=BC2+EC2x2=62+ (10-x)2解得 x = 6.8∴EC=10-6.8=3.2cm折叠问题: 如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕,若AB=9,BC=3,求FC的长?解:由已知AF=FC设AF=x,则FB = 9-x 在R t △FBC中,根据勾股定理:
FC2=FB2+BC2即 x2=(9-x)2+32解得 x=5
即 FC=5折叠问题:D′ x 矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕EF的长。ABCDFEx1010864(8-x)折叠问题:设EF = x 如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长是多少米?183024 在一棵树的10米高的D处有两只猴子,其中一只猴子爬下树走到离树20米的池塘A处,另一只爬到树顶后直接跃向池塘A处,如果两只猴子所经过的直线距离相等,试问这棵树有多高?DABC10米20米┏x 2、在直角三角形中,只知道一边的长度,另外两边只知道它们的关系时,运用勾股定理列方程方法求解。应用勾股定理解决实际问题的一般思路:方程思想是解决数学问题常用的重要思想 1、在解决实际问题时,首先要画出适当的示意图,将实际问题抽象为数学问题,并构建直角三角形模型,再运用勾股定理解决实际问题。感悟与收获请谈谈你的收获……作业:习题18 1第6 8 10 11 12
