有理数乘法
图片预览







文档简介
课件31张PPT。有理数的乘法 解:5×3 = 15 解: × =计算:
5 × 3
×
0 × 解:0 × = 0我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?问题:怎样计算
(1)
(2)如图,一只蜗牛沿直线l爬行,它现在的位置在l上的点O.lO(1)如果蜗牛一直以每分2CM的速度向右爬行,3分后它在什么位置?
(2)如果蜗牛一直以每分2CM的速度向左爬行,3分后它在什么位置?
(3)如果蜗牛一直以每分2CM的速度向右爬行,3分前它在什么位置?
(4)如果蜗牛一直以每分2CM的速度向左爬行,3分前它在什么位置?规定:向左为负,向右为正.
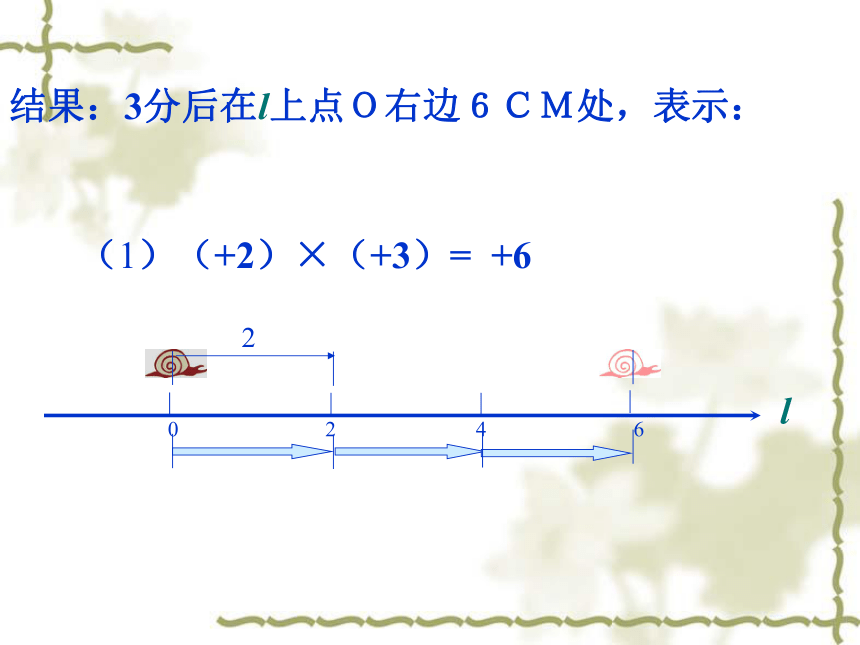
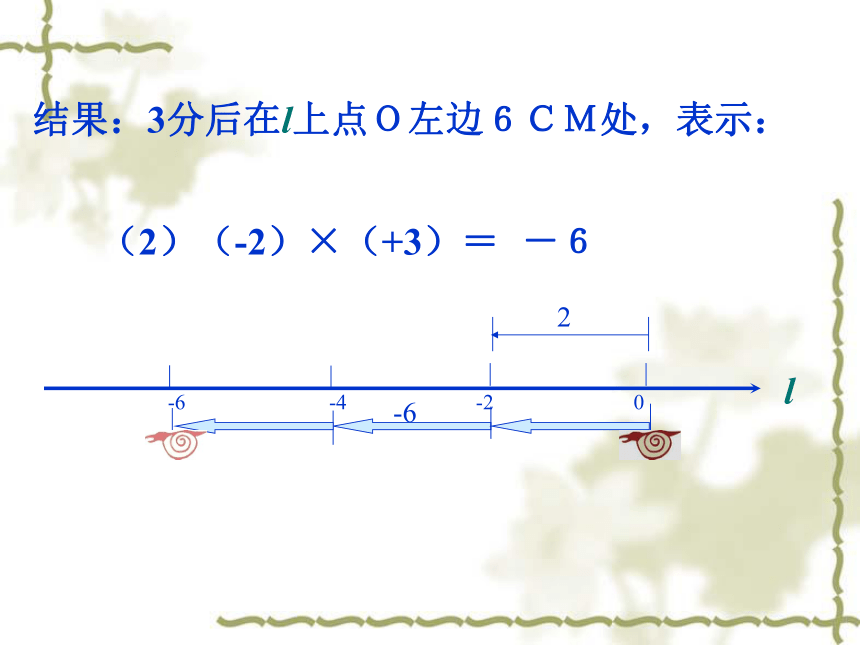
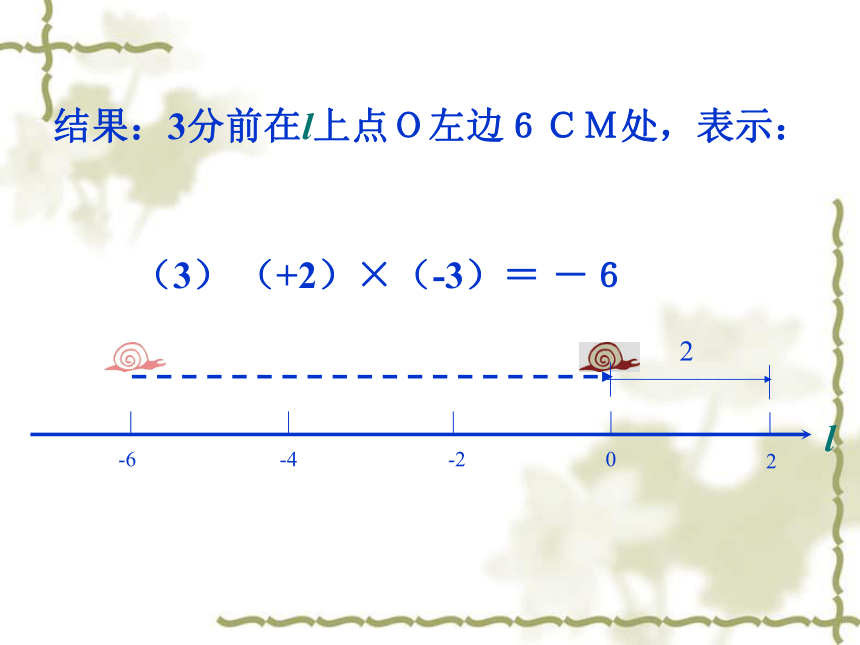
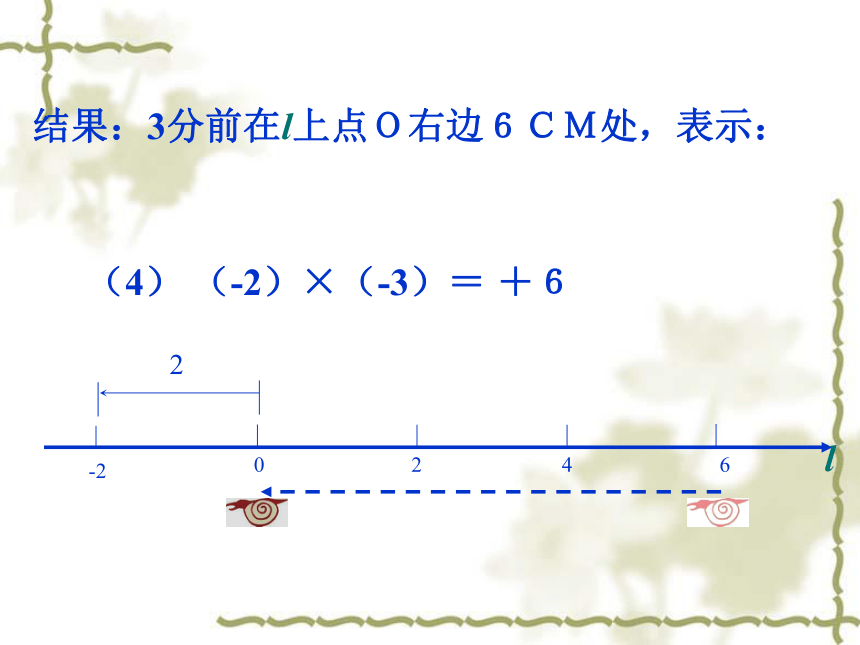
现在前为负,现在后为正.(1)(+2)×(+3)=结果:3分后在l上点O右边6CM处,表示:l+6(2)(-2)×(+3)=结果:3分后在l上点O左边6CM处,表示:-6l(3) (+2)×(-3)=结果:3分前在l上点O左边6CM处,表示:l-6(4) (-2)×(-3)= 结果:3分前在l上点O右边6CM处,表示:+6l观察(1)-(4)式,根据你对有理数乘法的思考,填空:
正数乘正数积为___数;
负数乘正数积为___数;
正数乘负数积为___数;
负数乘负数积为___数;
乘积的绝对值等于各乘数绝对值的___.正正负负积综合如下:
(1) 2×3=6
(2)(-2)×3= -6
(3) 2×(-3)= -6
(4)(-2)×(-3)=6
(5) 被乘数或乘数为0时,结果是0 有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。练习1:确定下列积的符号:
(1) 5×(-3)
(2) (-4)×6
(3) (-7)×(-9)
(4) 0.5×0.7积的符号为负
积的符号为负
积的符号为正
积的符号为正例如 (-5) ×(- 3)(同号两数相乘)(-5)×(- 3)= +( )(得正)5×3 = 15(把绝对值相乘)∴(-5)×(-3)=15又如:(-7)×4(异号两数相乘)(-7)×4= -( )(得负)7×4=28(把绝对值相乘)∴(-7)×4=-28注意:有理数相乘,先确定积的符号,在确定积的值解:(1) (-3) ×9 = -27注意:乘积是1的两个数互为倒数.一个数同+1相乘,得原数,一个数同-1相乘,得原数的相反数。 (3) 7 × (-1) =(4) (-0.8)× 1 = - 7 - 0.8例1 计算:
(1) (-3)×9 (2)( )×
(3) 7 ×(-1) (4) (-0.8)× 1(2) ( ) × =例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?解:(-6)×3=-18答:气温下降18 ℃.-54-24601.计算(口答):
(1)6×(-9)=
(2)(-4)×6=
(3)(-6)×(-1)=
(4)(-6) ×0=
(5) ×(- )=
(6)(- ) × =小结:1.有理数乘法法则: 两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0。2.如何进行两个有理数的运算: 先确定积的符号,再把绝对值相乘,当有一个因数为零时,积为零。有理数的乘法(1)算一算⑴ 2× ⑵ 0 ×7.5
⑶ 1×56 ⑷ 2×3
⑸ (-2)+(-2)+(-2)=-6式子(-2)+(-2)+(-2)
能写成乘法的形式吗?想一想,做一做:如何计算(-2)×3呢?由(-2)+(-2)+(-2)=-6.可知:(-2)×3=-6.观察与发现:观察: 2 × 3 = 6
比较:
(-2)× 3 = -6相反数相反数不 变发现:由(-2)×3=-6猜想:(-2)×(-3)=? 两数相乘,若把一个乘数换乘它的相反数,则所得积是原来的_______数.相反(-2)× 3 = -6
(-2)×(-3)=-(-6)=6 探讨:(-2)×(-3)=?不 变相反数相反数(-2)×(-3)=____.6 2 ×3 = 6 ⑴
(-2)×3 =-6 ⑵
(-2)×(-3)= 6 ⑶观察并填空:正数×正数=___数
正数×负数=___数
负数×负数=___数乘积的绝对值等于各乘数的绝对值的_____.正负正乘积归纳:有理数的乘法法则: 两数相乘,同号得___;异号得___;并把____相乘.正负绝对值应用:例1 计算:
⑴(-3)×9 ⑵(-5)×
⑶(-7)×1 ⑷(-4)×(-1)应用法则:有理数相乘,先确定积的_____;再确定积的_______.绝对值符号看谁做得又对又快:⑴6×(-9); ⑵(-4)×6;
⑶(-6)×(-1);⑷(-6)×9;
⑸ × ; ⑹ × .通过观察例1并结合小学学习的乘法法则讨论:⑴一个数同1相乘;得_______.
⑵一个数同-1相乘;得_________.
⑶一个数同0相乘;得_______.
⑷乘积是1的两个数是________.合作与交流原数原数相反数0互为倒数例2:用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1Km气温的变化量为-6oC,攀登3Km后,气温有什么变化?1.写出下列各数的倒数:
1,-1, , ,5, -5, , .动手又动脑2.观察并讨论:
⑴0有没有倒数?
⑵一个数的倒数等于它的本身,那么这个数是_____.
⑶如果两数互为相反数(0除外),那么它们的倒数也是互为相反数吗?课堂小结有理数的乘法法则: 两数相乘,同号得___;异号得___;并把_______相乘.有理数相乘,先确定积的_____;再确定积的______.符号绝对值绝对值正负GOODBYE!
5 × 3
×
0 × 解:0 × = 0我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?问题:怎样计算
(1)
(2)如图,一只蜗牛沿直线l爬行,它现在的位置在l上的点O.lO(1)如果蜗牛一直以每分2CM的速度向右爬行,3分后它在什么位置?
(2)如果蜗牛一直以每分2CM的速度向左爬行,3分后它在什么位置?
(3)如果蜗牛一直以每分2CM的速度向右爬行,3分前它在什么位置?
(4)如果蜗牛一直以每分2CM的速度向左爬行,3分前它在什么位置?规定:向左为负,向右为正.
现在前为负,现在后为正.(1)(+2)×(+3)=结果:3分后在l上点O右边6CM处,表示:l+6(2)(-2)×(+3)=结果:3分后在l上点O左边6CM处,表示:-6l(3) (+2)×(-3)=结果:3分前在l上点O左边6CM处,表示:l-6(4) (-2)×(-3)= 结果:3分前在l上点O右边6CM处,表示:+6l观察(1)-(4)式,根据你对有理数乘法的思考,填空:
正数乘正数积为___数;
负数乘正数积为___数;
正数乘负数积为___数;
负数乘负数积为___数;
乘积的绝对值等于各乘数绝对值的___.正正负负积综合如下:
(1) 2×3=6
(2)(-2)×3= -6
(3) 2×(-3)= -6
(4)(-2)×(-3)=6
(5) 被乘数或乘数为0时,结果是0 有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。练习1:确定下列积的符号:
(1) 5×(-3)
(2) (-4)×6
(3) (-7)×(-9)
(4) 0.5×0.7积的符号为负
积的符号为负
积的符号为正
积的符号为正例如 (-5) ×(- 3)(同号两数相乘)(-5)×(- 3)= +( )(得正)5×3 = 15(把绝对值相乘)∴(-5)×(-3)=15又如:(-7)×4(异号两数相乘)(-7)×4= -( )(得负)7×4=28(把绝对值相乘)∴(-7)×4=-28注意:有理数相乘,先确定积的符号,在确定积的值解:(1) (-3) ×9 = -27注意:乘积是1的两个数互为倒数.一个数同+1相乘,得原数,一个数同-1相乘,得原数的相反数。 (3) 7 × (-1) =(4) (-0.8)× 1 = - 7 - 0.8例1 计算:
(1) (-3)×9 (2)( )×
(3) 7 ×(-1) (4) (-0.8)× 1(2) ( ) × =例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?解:(-6)×3=-18答:气温下降18 ℃.-54-24601.计算(口答):
(1)6×(-9)=
(2)(-4)×6=
(3)(-6)×(-1)=
(4)(-6) ×0=
(5) ×(- )=
(6)(- ) × =小结:1.有理数乘法法则: 两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0。2.如何进行两个有理数的运算: 先确定积的符号,再把绝对值相乘,当有一个因数为零时,积为零。有理数的乘法(1)算一算⑴ 2× ⑵ 0 ×7.5
⑶ 1×56 ⑷ 2×3
⑸ (-2)+(-2)+(-2)=-6式子(-2)+(-2)+(-2)
能写成乘法的形式吗?想一想,做一做:如何计算(-2)×3呢?由(-2)+(-2)+(-2)=-6.可知:(-2)×3=-6.观察与发现:观察: 2 × 3 = 6
比较:
(-2)× 3 = -6相反数相反数不 变发现:由(-2)×3=-6猜想:(-2)×(-3)=? 两数相乘,若把一个乘数换乘它的相反数,则所得积是原来的_______数.相反(-2)× 3 = -6
(-2)×(-3)=-(-6)=6 探讨:(-2)×(-3)=?不 变相反数相反数(-2)×(-3)=____.6 2 ×3 = 6 ⑴
(-2)×3 =-6 ⑵
(-2)×(-3)= 6 ⑶观察并填空:正数×正数=___数
正数×负数=___数
负数×负数=___数乘积的绝对值等于各乘数的绝对值的_____.正负正乘积归纳:有理数的乘法法则: 两数相乘,同号得___;异号得___;并把____相乘.正负绝对值应用:例1 计算:
⑴(-3)×9 ⑵(-5)×
⑶(-7)×1 ⑷(-4)×(-1)应用法则:有理数相乘,先确定积的_____;再确定积的_______.绝对值符号看谁做得又对又快:⑴6×(-9); ⑵(-4)×6;
⑶(-6)×(-1);⑷(-6)×9;
⑸ × ; ⑹ × .通过观察例1并结合小学学习的乘法法则讨论:⑴一个数同1相乘;得_______.
⑵一个数同-1相乘;得_________.
⑶一个数同0相乘;得_______.
⑷乘积是1的两个数是________.合作与交流原数原数相反数0互为倒数例2:用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1Km气温的变化量为-6oC,攀登3Km后,气温有什么变化?1.写出下列各数的倒数:
1,-1, , ,5, -5, , .动手又动脑2.观察并讨论:
⑴0有没有倒数?
⑵一个数的倒数等于它的本身,那么这个数是_____.
⑶如果两数互为相反数(0除外),那么它们的倒数也是互为相反数吗?课堂小结有理数的乘法法则: 两数相乘,同号得___;异号得___;并把_______相乘.有理数相乘,先确定积的_____;再确定积的______.符号绝对值绝对值正负GOODBYE!
