1.1 探索勾股定理 第1课时 北师大版八年级上册数学 课件(19张PPT)
文档属性
| 名称 | 1.1 探索勾股定理 第1课时 北师大版八年级上册数学 课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
第1课时
第一章 勾股定理
1.1 探索勾股定理
1.会用数格子的办法探索勾股定理,体会数学与现实生活的紧密联系.
一、学习目标
2.知道直角三角形的三边之间的数量关系,并能用勾股定理解决一些简单的实际问题.
二、新课导入
由于安全问题,工人小戴打算加一条钢索用来稳固
电线杆.从电线杆离地面8m处向地面拉一条钢索,如果这
条钢索在地面的固定点距离电线杆底部6m,那么工人小戴应准备多长的钢索?
三、概念剖析
想一想
(1)在纸上画若干个直角三角形,分别测量它们的三条边,看看三条边的平方之间有怎样的关系?与同伴进行交流.
三、概念剖析
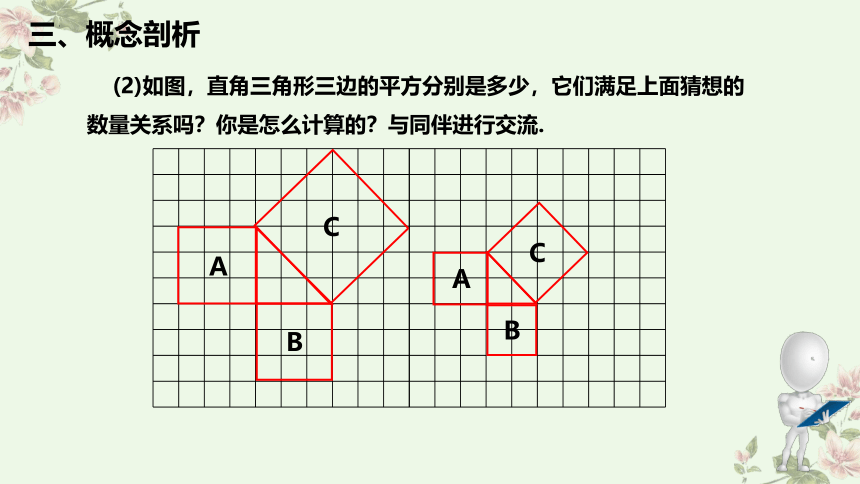
(2)如图,直角三角形三边的平方分别是多少,它们满足上面猜想的数量关系吗?你是怎么计算的?与同伴进行交流.
A
A
B
B
C
C
三、概念剖析
A
B
C
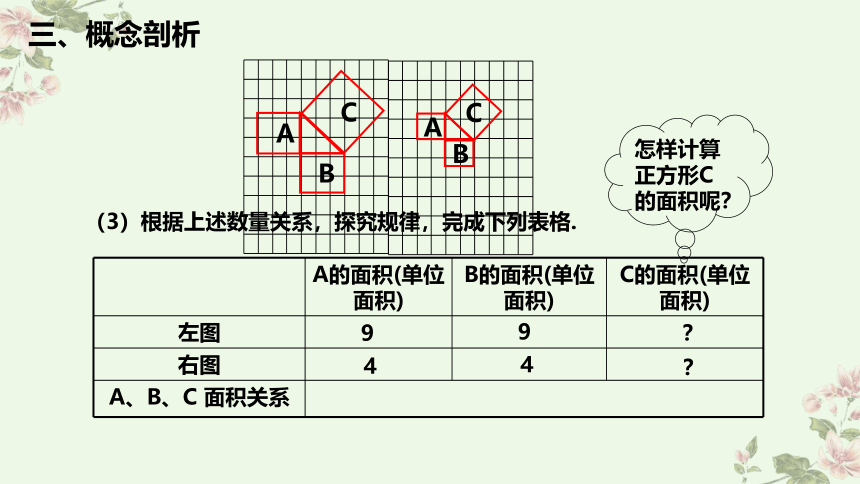
(3)根据上述数量关系,探究规律,完成下列表格.
A的面积(单位
面积) B的面积(单位
面积) C的面积(单位
面积)
左图
右图
A、B、C 面积关系
A
B
C
4
4
?
9
9
?
怎样计算正方形C的面积呢?
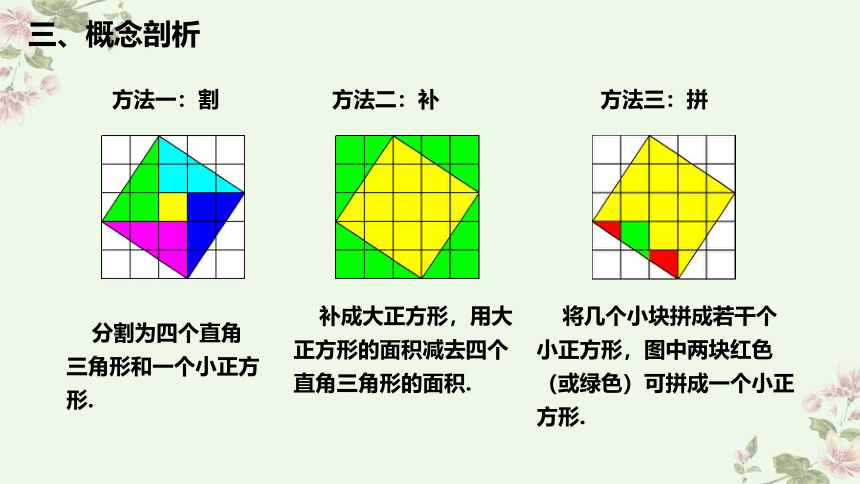
方法一:割
方法二:补
方法三:拼
分割为四个直角三角形和一个小正方形.
补成大正方形,用大正方形的面积减去四个直角三角形的面积.
将几个小块拼成若干个小正方形,图中两块红色(或绿色)可拼成一个小正方形.
三、概念剖析
三、概念剖析
A
B
C
(3)根据上述数量关系,探究规律,完成下列表格.
A的面积(单位
面积) B的面积(单位
面积) C的面积(单位
面积)
左图
右图
A、B、C 面积关系
A
B
C
4
4
8
9
9
18
SA+SB=SC
三、概念剖析
(3)对于下图中的直角三角形是否还满足上述的数量关系?
A
A
B
B
C
C
三、概念剖析
通过上述活动,我们可以发现,直角三角形两直角边的平方和等于斜边的平方和.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.因此,我国称此结论为勾股定理.
A
B
C
a
b
c
勾股定理:直角三角形两直角边的平方和等于斜边的平方
SA=a2
SB=b2
SC=c2
a2+b2=c2
SA+SB=SC
四、典型例题
8
6
A
B
C
例1:求图中直角三角形的未知边的长度.
解:在Rt△ABC中,∠B=90°,AB=8,BC=6.
根据勾股定理可得:
AC2=AB2+BC2=82+62=100
∴AC= 10
四、典型例题
例2:如图,每个小正方形的边长为1,a,b,c是△ABC的三边,求△ABC的周长.
解:由网格可知:
b= =5;
a= = ;
c=4;
a+b+c=5+ +4=9+
∴△ABC的周长是9+
四、典型例题
归纳总结
在运用勾股定理时,首先要正确识别哪个角是直角,从而确定哪条边是斜边,然后准确写出勾股定理表达式进行求解.
【当堂检测】
1.图中,每个小正方形的边长为1,△ABC的三边a、b、c的大小关系是( )
A.a<c<b
B.a<b<c
C.c<a<b
D.c<b<a
C
【当堂检测】
2.求斜边长为17 cm、一条直角边长为15 cm的直角三角形的面积.
解:设另一条直角边长是x cm.由勾股定理得:
152+ x2 =172,x2=172-152=289–225=64,
解得 x=±8(负值舍去),
所以另一直角边长为8 cm,
故直角三角形的面积是:
(cm2).
四、典型例题
例3: 一架5 m的梯子斜靠在一竖直的墙上,这时梯子的顶端距墙角4 m,若梯子的顶端下滑1 m,底端水平滑动多少米?
解:底端水平滑动1米
在Rt△ABC中,BC2=AB2-AC2=52-42=32,
即BC=3,在Rt△DCE中,CE=AC-AE=3,DE=5,
所以DC2=DE2-CE2=52-32=42,
即DC=4,所以BD=4-3=1(米)
【当堂检测】
3.如图,是一长方形公园,如果某人从景点A走到景点D,则至少要走( ) 米.
A. 15 B. 17 C. 19 D. 21
B
A
B
C
D
8米
15米
【当堂检测】
4.一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少
A
B
C
解:在Rt△ABC中,根据勾股定理,得:
BC2=AB2-AC2 =2.52-2.42 =0.49,
所以BC=0.7.
答:梯脚与墙的距离是0.7米.
五、课堂总结
认识勾股定理
直角三角形两直角边的平方和等于斜边的平方.如果用a、b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2 .
第1课时
第一章 勾股定理
1.1 探索勾股定理
1.会用数格子的办法探索勾股定理,体会数学与现实生活的紧密联系.
一、学习目标
2.知道直角三角形的三边之间的数量关系,并能用勾股定理解决一些简单的实际问题.
二、新课导入
由于安全问题,工人小戴打算加一条钢索用来稳固
电线杆.从电线杆离地面8m处向地面拉一条钢索,如果这
条钢索在地面的固定点距离电线杆底部6m,那么工人小戴应准备多长的钢索?
三、概念剖析
想一想
(1)在纸上画若干个直角三角形,分别测量它们的三条边,看看三条边的平方之间有怎样的关系?与同伴进行交流.
三、概念剖析
(2)如图,直角三角形三边的平方分别是多少,它们满足上面猜想的数量关系吗?你是怎么计算的?与同伴进行交流.
A
A
B
B
C
C
三、概念剖析
A
B
C
(3)根据上述数量关系,探究规律,完成下列表格.
A的面积(单位
面积) B的面积(单位
面积) C的面积(单位
面积)
左图
右图
A、B、C 面积关系
A
B
C
4
4
?
9
9
?
怎样计算正方形C的面积呢?
方法一:割
方法二:补
方法三:拼
分割为四个直角三角形和一个小正方形.
补成大正方形,用大正方形的面积减去四个直角三角形的面积.
将几个小块拼成若干个小正方形,图中两块红色(或绿色)可拼成一个小正方形.
三、概念剖析
三、概念剖析
A
B
C
(3)根据上述数量关系,探究规律,完成下列表格.
A的面积(单位
面积) B的面积(单位
面积) C的面积(单位
面积)
左图
右图
A、B、C 面积关系
A
B
C
4
4
8
9
9
18
SA+SB=SC
三、概念剖析
(3)对于下图中的直角三角形是否还满足上述的数量关系?
A
A
B
B
C
C
三、概念剖析
通过上述活动,我们可以发现,直角三角形两直角边的平方和等于斜边的平方和.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.因此,我国称此结论为勾股定理.
A
B
C
a
b
c
勾股定理:直角三角形两直角边的平方和等于斜边的平方
SA=a2
SB=b2
SC=c2
a2+b2=c2
SA+SB=SC
四、典型例题
8
6
A
B
C
例1:求图中直角三角形的未知边的长度.
解:在Rt△ABC中,∠B=90°,AB=8,BC=6.
根据勾股定理可得:
AC2=AB2+BC2=82+62=100
∴AC= 10
四、典型例题
例2:如图,每个小正方形的边长为1,a,b,c是△ABC的三边,求△ABC的周长.
解:由网格可知:
b= =5;
a= = ;
c=4;
a+b+c=5+ +4=9+
∴△ABC的周长是9+
四、典型例题
归纳总结
在运用勾股定理时,首先要正确识别哪个角是直角,从而确定哪条边是斜边,然后准确写出勾股定理表达式进行求解.
【当堂检测】
1.图中,每个小正方形的边长为1,△ABC的三边a、b、c的大小关系是( )
A.a<c<b
B.a<b<c
C.c<a<b
D.c<b<a
C
【当堂检测】
2.求斜边长为17 cm、一条直角边长为15 cm的直角三角形的面积.
解:设另一条直角边长是x cm.由勾股定理得:
152+ x2 =172,x2=172-152=289–225=64,
解得 x=±8(负值舍去),
所以另一直角边长为8 cm,
故直角三角形的面积是:
(cm2).
四、典型例题
例3: 一架5 m的梯子斜靠在一竖直的墙上,这时梯子的顶端距墙角4 m,若梯子的顶端下滑1 m,底端水平滑动多少米?
解:底端水平滑动1米
在Rt△ABC中,BC2=AB2-AC2=52-42=32,
即BC=3,在Rt△DCE中,CE=AC-AE=3,DE=5,
所以DC2=DE2-CE2=52-32=42,
即DC=4,所以BD=4-3=1(米)
【当堂检测】
3.如图,是一长方形公园,如果某人从景点A走到景点D,则至少要走( ) 米.
A. 15 B. 17 C. 19 D. 21
B
A
B
C
D
8米
15米
【当堂检测】
4.一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少
A
B
C
解:在Rt△ABC中,根据勾股定理,得:
BC2=AB2-AC2 =2.52-2.42 =0.49,
所以BC=0.7.
答:梯脚与墙的距离是0.7米.
五、课堂总结
认识勾股定理
直角三角形两直角边的平方和等于斜边的平方.如果用a、b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2 .
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
