1.2 矩形的性质与判定 第1课时 北师大版九年级上册数学 课件(15张PPT)
文档属性
| 名称 | 1.2 矩形的性质与判定 第1课时 北师大版九年级上册数学 课件(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 09:05:38 | ||
图片预览




文档简介
(共15张PPT)
1.2 矩形的性质与判定
第1课时
第一章 特殊平行四边形
1.理解矩形的定义,知道矩形是特殊的平行四边形.
2.掌握矩形和直角三角形的性质定理,会进行有关的计算与证明.
任务一:掌握矩形和直角三角形的性质定理
活动1:请观察下面平行四边形的变化,完成下列问题.
(1)当平行四边形一个角是直角时停止,这个图形有何特点 它还是平行四边形吗?请举出身边类似图形的例子.
(2)平行四边形一定是矩形吗 矩形一定是平行四边形吗 由此你能得出什么结论,请说一说.
有一个角是直角的平行四边形叫做矩形.
矩形是特殊的平行四边形.平行四边形不一定是矩形.
活动2:动手做一做.
(1)任意度量身边一个矩形物体的每个角的度数,如数学书本、课桌等.
(2)拿出一张A4纸,分别画出它的两条对角线,再分别量出两条对角线的长度.
通过(1)(2)的操作说说你的猜想,并加以验证.
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
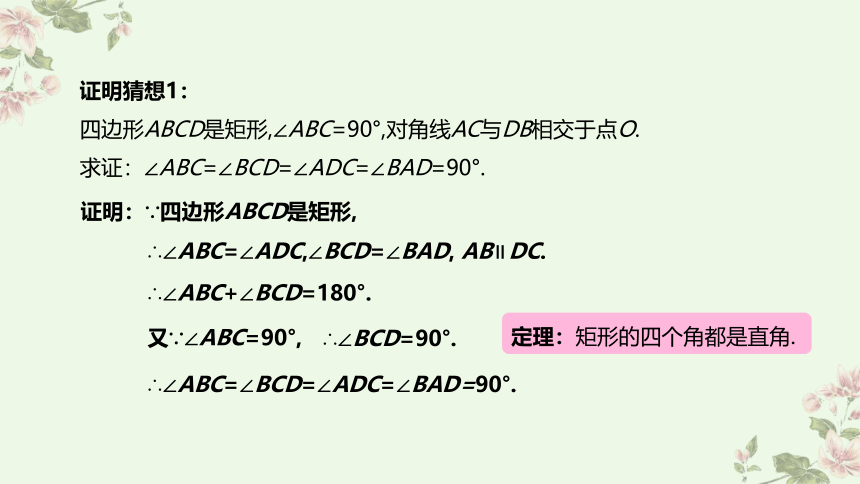
证明猜想1:
四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.
求证:∠ABC=∠BCD=∠ADC=∠BAD=90°.
证明:∵四边形ABCD是矩形,
∴∠ABC=∠ADC,∠BCD=∠BAD, AB∥DC.
∴∠ABC+∠BCD=180°.
又∵∠ABC=90°,
∴∠BCD=90°.
∴∠ABC=∠BCD=∠ADC=∠BAD=90°.
定理:矩形的四个角都是直角.
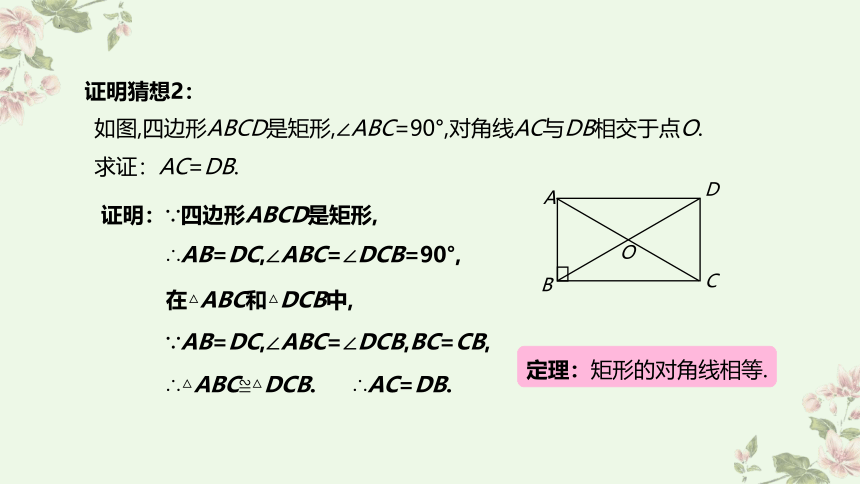
如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.
求证:AC=DB.
A
B
C
D
O
证明:∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC=CB,
∴△ABC≌△DCB.
∴AC=DB.
证明猜想2:
定理:矩形的对角线相等.
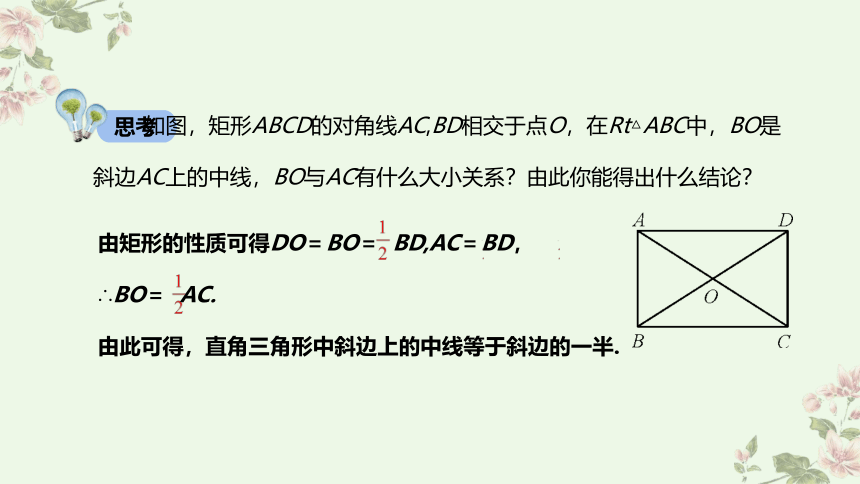
思考
如图,矩形ABCD的对角线AC,BD相交于点O,在Rt△ABC中,BO是斜边AC上的中线,BO与AC有什么大小关系?由此你能得出什么结论?
由矩形的性质可得DO=BO= BD,AC=BD,
∴BO= AC.
由此可得,直角三角形中斜边上的中线等于斜边的一半.
练一练
如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的_______.
活动:解决下列问题,简要归纳所用到的性质或方法.
(1)在矩形ABCD中,两条对角线AC,BD相交于点O,
∠AOB=60°,AB=4,求矩形对角线的长.
(2)已知:如图2,矩形ABCD中,E是BC上一点,
DF⊥AE于点F,若AE=BC.求证:CE=EF
图2
任务二:能运用矩形和直角三角形的性质定理解决相关问题
(1)在矩形ABCD中,两条对角线AC,BD相交于点O,∠AOB=60°,AB=4,求矩形对角线的长.
解:(1)∵四边形ABCD是矩形,
∴AC与BD相等且互相平分,
∴OA=OB.
又∵∠AOB=60°,
∴△OAB是等边三角形,
∴OA=AB=4,
∴AC=BD=2OA=8.
(2)已知:如图2,矩形ABCD中,E是BC上一点,DF⊥AE于点F,若AE=BC.
求证:CE=EF.
图2
证明:∵ 四边形ABCD是矩形,∴∠B=90°,AD∥BC,且AD=BC.
∴∠1=∠2,AE=AD.
∵DF⊥AE,∴∠DFA=90°.
在△ABE与△DFA中,
∠B=∠DFA,
AE=AD,
∠1=∠2,
∴△ABE≌△DFA(AAS),∴AF=BE,∴EF=EC.
练一练
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是AB边上的中线,若AD=3,CE=5,求CD的长.
解:∵在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=5,
∵AD=3,
∵CD为AB边上的高,
∴在Rt△CDE中,CE2=CD2+DE2,
∴DE=AE-AD=5-3=2,
∴AE=CE=5,
即52=CD2+22,
∴CD= .
1.如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD
C.OA=OB D.OA=AD
D
2.矩形的两条对角线的一个夹角为60°,一条对角线与短边的和是15,则对角线长为 ,短边长为 .
10
5
3.如图,在矩形ABCD中,点E是CD边上的中点.求证:AE=BE.
证明:∵四边形ABCD是矩形,
∴AD=BC,∠D=∠C=90°,
∵E为CD边上的中点,
∴DE=CE,
∴△ADE≌△BCE(SAS),
∴AE=BE.
针对本节课所学内容,说说你都学到了哪些知识?
计算与论证
1.2 矩形的性质与判定
第1课时
第一章 特殊平行四边形
1.理解矩形的定义,知道矩形是特殊的平行四边形.
2.掌握矩形和直角三角形的性质定理,会进行有关的计算与证明.
任务一:掌握矩形和直角三角形的性质定理
活动1:请观察下面平行四边形的变化,完成下列问题.
(1)当平行四边形一个角是直角时停止,这个图形有何特点 它还是平行四边形吗?请举出身边类似图形的例子.
(2)平行四边形一定是矩形吗 矩形一定是平行四边形吗 由此你能得出什么结论,请说一说.
有一个角是直角的平行四边形叫做矩形.
矩形是特殊的平行四边形.平行四边形不一定是矩形.
活动2:动手做一做.
(1)任意度量身边一个矩形物体的每个角的度数,如数学书本、课桌等.
(2)拿出一张A4纸,分别画出它的两条对角线,再分别量出两条对角线的长度.
通过(1)(2)的操作说说你的猜想,并加以验证.
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
证明猜想1:
四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.
求证:∠ABC=∠BCD=∠ADC=∠BAD=90°.
证明:∵四边形ABCD是矩形,
∴∠ABC=∠ADC,∠BCD=∠BAD, AB∥DC.
∴∠ABC+∠BCD=180°.
又∵∠ABC=90°,
∴∠BCD=90°.
∴∠ABC=∠BCD=∠ADC=∠BAD=90°.
定理:矩形的四个角都是直角.
如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.
求证:AC=DB.
A
B
C
D
O
证明:∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC=CB,
∴△ABC≌△DCB.
∴AC=DB.
证明猜想2:
定理:矩形的对角线相等.
思考
如图,矩形ABCD的对角线AC,BD相交于点O,在Rt△ABC中,BO是斜边AC上的中线,BO与AC有什么大小关系?由此你能得出什么结论?
由矩形的性质可得DO=BO= BD,AC=BD,
∴BO= AC.
由此可得,直角三角形中斜边上的中线等于斜边的一半.
练一练
如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的_______.
活动:解决下列问题,简要归纳所用到的性质或方法.
(1)在矩形ABCD中,两条对角线AC,BD相交于点O,
∠AOB=60°,AB=4,求矩形对角线的长.
(2)已知:如图2,矩形ABCD中,E是BC上一点,
DF⊥AE于点F,若AE=BC.求证:CE=EF
图2
任务二:能运用矩形和直角三角形的性质定理解决相关问题
(1)在矩形ABCD中,两条对角线AC,BD相交于点O,∠AOB=60°,AB=4,求矩形对角线的长.
解:(1)∵四边形ABCD是矩形,
∴AC与BD相等且互相平分,
∴OA=OB.
又∵∠AOB=60°,
∴△OAB是等边三角形,
∴OA=AB=4,
∴AC=BD=2OA=8.
(2)已知:如图2,矩形ABCD中,E是BC上一点,DF⊥AE于点F,若AE=BC.
求证:CE=EF.
图2
证明:∵ 四边形ABCD是矩形,∴∠B=90°,AD∥BC,且AD=BC.
∴∠1=∠2,AE=AD.
∵DF⊥AE,∴∠DFA=90°.
在△ABE与△DFA中,
∠B=∠DFA,
AE=AD,
∠1=∠2,
∴△ABE≌△DFA(AAS),∴AF=BE,∴EF=EC.
练一练
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是AB边上的中线,若AD=3,CE=5,求CD的长.
解:∵在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=5,
∵AD=3,
∵CD为AB边上的高,
∴在Rt△CDE中,CE2=CD2+DE2,
∴DE=AE-AD=5-3=2,
∴AE=CE=5,
即52=CD2+22,
∴CD= .
1.如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD
C.OA=OB D.OA=AD
D
2.矩形的两条对角线的一个夹角为60°,一条对角线与短边的和是15,则对角线长为 ,短边长为 .
10
5
3.如图,在矩形ABCD中,点E是CD边上的中点.求证:AE=BE.
证明:∵四边形ABCD是矩形,
∴AD=BC,∠D=∠C=90°,
∵E为CD边上的中点,
∴DE=CE,
∴△ADE≌△BCE(SAS),
∴AE=BE.
针对本节课所学内容,说说你都学到了哪些知识?
计算与论证
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
