4.3 相似多边形 课件(14张PPT) 北师大版数学九年级上册
文档属性
| 名称 | 4.3 相似多边形 课件(14张PPT) 北师大版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 09:29:26 | ||
图片预览





文档简介
(共14张PPT)
4.3 相似多边形
第四章 图形的相似
1.经历相似多边形概念的形成过程,了解相似多边形的含义.
2.会根据条件判断两个多边形是否为相似多边形.
观察下列图形,小组讨论,回答下列问题.
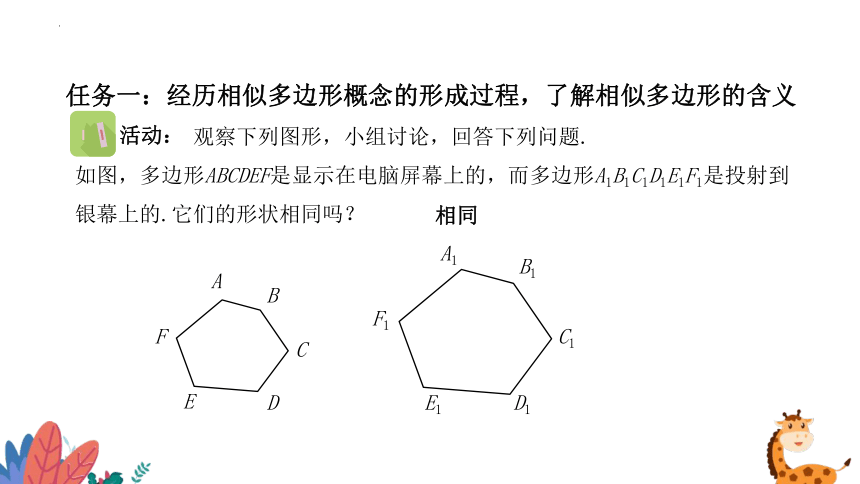
如图,多边形ABCDEF是显示在电脑屏幕上的,而多边形A1B1C1D1E1F1是投射到银幕上的.它们的形状相同吗?
活动:
任务一:经历相似多边形概念的形成过程,了解相似多边形的含义
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
相同
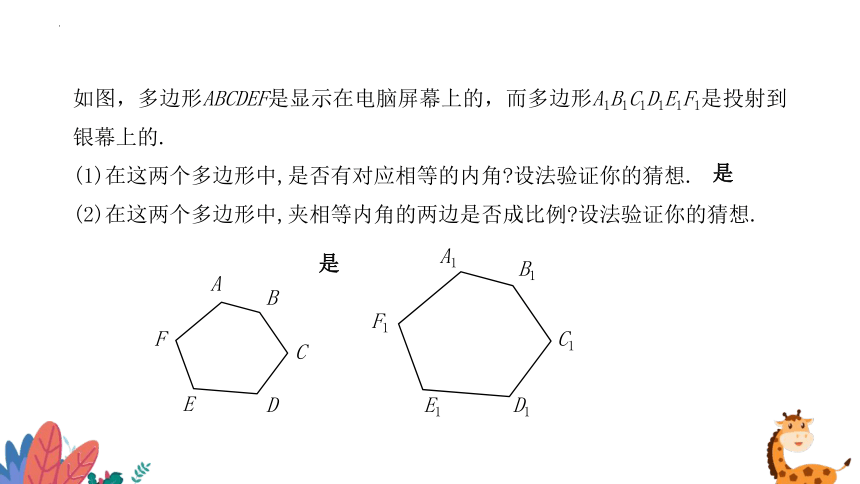
如图,多边形ABCDEF是显示在电脑屏幕上的,而多边形A1B1C1D1E1F1是投射到银幕上的.
(1)在这两个多边形中,是否有对应相等的内角 设法验证你的猜想.
(2)在这两个多边形中,夹相等内角的两边是否成比例 设法验证你的猜想.
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
是
是
新知生成
各角分别相等、各边成比例的两个多边形叫做相似多边形.
相似多边形的对应边的比叫做相似比.
相似多边形的对应角相等,对应边成比例.
3.相似比:
2.相似多边形的性质:
1.相似多边形的概念:
相似多边形用符号“∽”表示,读作“相似于”.
思考1:任意两个等边三角形相似吗?任意两个正方形呢?任意正n边形呢?
思考2:任意的两个菱形是否相似?
归纳:任意两个边数相等正多边形都相似.
任意两个菱形满足“各边成比例”,但不一定满足“各角分别相等”的条件.因此,任意两个菱形不一定相似.如下图两个菱形不相似.
活动探究
学习目标
当堂检测
课堂总结
练一练
下列判断正确的是( )
A.所有的直角三角形都相似
B.所有的等腰直角三角形都相似
C.所有的菱形都相似
D.所有的矩形都相似
B
活动:如图,矩形ABCD的长AB=30,宽BC=20.完成下列问题.
问题:(1)如图①,若沿矩形ABCD四周有宽为1的环形区域,图中所形成的两个矩形ABCD与A'B'C'D'相似吗 请说明理由.
又∵AB=30,BC=20,∴A'B'=28,B'C'=18,
∴矩形ABCD和矩形A'B'C'D'不相似.
解:(1)∵四边形ABCD和四边形A'B'C'D'为矩形,
∴对应角相等,均为90°,
任务二:会根据条件判断两个多边形是否为相似多边形
如图,矩形ABCD的长AB=30,宽BC=20.
(2)如图②,x为多少时,图中的两个矩形ABCD与A'B'C'D'相似
1
1
解:(2)当矩形ABCD∽矩形A'B'C'D',有
即
解得:x=1.5;
当矩形ABCD∽矩形B'C'D'A',有
即
解得:x=9;
综上所述:x=1.5或9时,矩形ABCD与A'B'C'D'相似.
归纳总结
判断两个多边形相似,必须同时满足的条件:
①对应角相等;
②对应边长度的比相等.
注意:1.二者缺一不可.
2.在记两个多边形相似时,要把表示对应角顶点的字母写在对应的位置上.
活动探究
学习目标
当堂检测
课堂总结
练一练
填空.
(1) 如图①是两个相似的四边形,
则x= ,y = ,
α= ;
(2) 如图②是两个相似的矩形,
x= .
2.5
1.5
90°
22.5
╰
65°
╯
80°
α
╭
125°
╯
80°
╮
3
x
y
图①
3
5
30
20
15
x
图②
6
1.五边形ABCDE相似于五边形A'B'C'D'E',它们的相似比为1 : 3,
(1)若∠D=135°,则∠D'=______;
(2)若A'B'=15cm,则AB=______.
135°
5cm
2.一个多边形的边长分别是2、3、4、5、6,另一个和它相似的多边形的最短边长为6,则这个多边形的最长边为______.
18
3.如图,已知:∠ACB =∠ADC =90°,AD=2,CD= ,当AB为何值时,△ACB与△ADC相似.
C
A
B
D
解:∵∠ADC=90°,AD=2,CD= ,
∴在Rt△ADC中,AC= .
当△ACB∽△ADC时,AB:AC=AC:AD,
即 ,
∴AB=3.
当△ACB∽△CDA时,AB:AC=AC:CD,
即 ,
综上所述:AB=3或 时,△ACB与△ADC相似.
针对本节课所学内容,说说你都学到了哪些知识?
相似多边形
概念
性质:相似多边形的对应角相等,对应边成比例.
相似比
4.3 相似多边形
第四章 图形的相似
1.经历相似多边形概念的形成过程,了解相似多边形的含义.
2.会根据条件判断两个多边形是否为相似多边形.
观察下列图形,小组讨论,回答下列问题.
如图,多边形ABCDEF是显示在电脑屏幕上的,而多边形A1B1C1D1E1F1是投射到银幕上的.它们的形状相同吗?
活动:
任务一:经历相似多边形概念的形成过程,了解相似多边形的含义
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
相同
如图,多边形ABCDEF是显示在电脑屏幕上的,而多边形A1B1C1D1E1F1是投射到银幕上的.
(1)在这两个多边形中,是否有对应相等的内角 设法验证你的猜想.
(2)在这两个多边形中,夹相等内角的两边是否成比例 设法验证你的猜想.
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
是
是
新知生成
各角分别相等、各边成比例的两个多边形叫做相似多边形.
相似多边形的对应边的比叫做相似比.
相似多边形的对应角相等,对应边成比例.
3.相似比:
2.相似多边形的性质:
1.相似多边形的概念:
相似多边形用符号“∽”表示,读作“相似于”.
思考1:任意两个等边三角形相似吗?任意两个正方形呢?任意正n边形呢?
思考2:任意的两个菱形是否相似?
归纳:任意两个边数相等正多边形都相似.
任意两个菱形满足“各边成比例”,但不一定满足“各角分别相等”的条件.因此,任意两个菱形不一定相似.如下图两个菱形不相似.
活动探究
学习目标
当堂检测
课堂总结
练一练
下列判断正确的是( )
A.所有的直角三角形都相似
B.所有的等腰直角三角形都相似
C.所有的菱形都相似
D.所有的矩形都相似
B
活动:如图,矩形ABCD的长AB=30,宽BC=20.完成下列问题.
问题:(1)如图①,若沿矩形ABCD四周有宽为1的环形区域,图中所形成的两个矩形ABCD与A'B'C'D'相似吗 请说明理由.
又∵AB=30,BC=20,∴A'B'=28,B'C'=18,
∴矩形ABCD和矩形A'B'C'D'不相似.
解:(1)∵四边形ABCD和四边形A'B'C'D'为矩形,
∴对应角相等,均为90°,
任务二:会根据条件判断两个多边形是否为相似多边形
如图,矩形ABCD的长AB=30,宽BC=20.
(2)如图②,x为多少时,图中的两个矩形ABCD与A'B'C'D'相似
1
1
解:(2)当矩形ABCD∽矩形A'B'C'D',有
即
解得:x=1.5;
当矩形ABCD∽矩形B'C'D'A',有
即
解得:x=9;
综上所述:x=1.5或9时,矩形ABCD与A'B'C'D'相似.
归纳总结
判断两个多边形相似,必须同时满足的条件:
①对应角相等;
②对应边长度的比相等.
注意:1.二者缺一不可.
2.在记两个多边形相似时,要把表示对应角顶点的字母写在对应的位置上.
活动探究
学习目标
当堂检测
课堂总结
练一练
填空.
(1) 如图①是两个相似的四边形,
则x= ,y = ,
α= ;
(2) 如图②是两个相似的矩形,
x= .
2.5
1.5
90°
22.5
╰
65°
╯
80°
α
╭
125°
╯
80°
╮
3
x
y
图①
3
5
30
20
15
x
图②
6
1.五边形ABCDE相似于五边形A'B'C'D'E',它们的相似比为1 : 3,
(1)若∠D=135°,则∠D'=______;
(2)若A'B'=15cm,则AB=______.
135°
5cm
2.一个多边形的边长分别是2、3、4、5、6,另一个和它相似的多边形的最短边长为6,则这个多边形的最长边为______.
18
3.如图,已知:∠ACB =∠ADC =90°,AD=2,CD= ,当AB为何值时,△ACB与△ADC相似.
C
A
B
D
解:∵∠ADC=90°,AD=2,CD= ,
∴在Rt△ADC中,AC= .
当△ACB∽△ADC时,AB:AC=AC:AD,
即 ,
∴AB=3.
当△ACB∽△CDA时,AB:AC=AC:CD,
即 ,
综上所述:AB=3或 时,△ACB与△ADC相似.
针对本节课所学内容,说说你都学到了哪些知识?
相似多边形
概念
性质:相似多边形的对应角相等,对应边成比例.
相似比
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
