第一章 勾股定理复习课课件 21张PPT 北师大版八年级上册数学
文档属性
| 名称 | 第一章 勾股定理复习课课件 21张PPT 北师大版八年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 534.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 09:55:52 | ||
图片预览





文档简介
(共21张PPT)
第一章 勾股定理
复习课
2.能把简单的立体图形转化为平面图形,构造直角三角形求线段长.
一、学习目标
1.知道勾股定理及其逆定理,并会灵活运用解决简单的几何问题和生活实际问题.
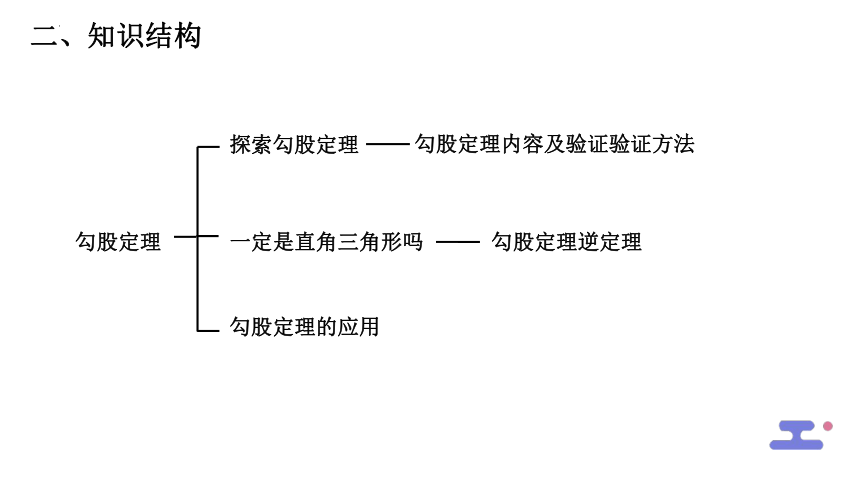
二、知识结构
探索勾股定理
勾股定理的应用
勾股定理
一定是直角三角形吗
勾股定理内容及验证验证方法
勾股定理逆定理
三、概念剖析
(一)勾股定理
勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用a、b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2 .
勾股定理的验证:可以采用测量、数格子、割补法,通过构造几何图形,并计算图形面积得出一个等式,从而验证勾股定理.
三、概念剖析
(二)勾股定理逆定理
勾股定理逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
勾股数:满足a2+b2=c2的三个正整数,称为勾股数.
勾股定理逆定理是用来判断一个三角形是否是直角三角形,应用时首先确定该三角形的最大边,当其余两边的平方和等于最大边的平方时,该三角形才是直角三角形.
三、概念剖析
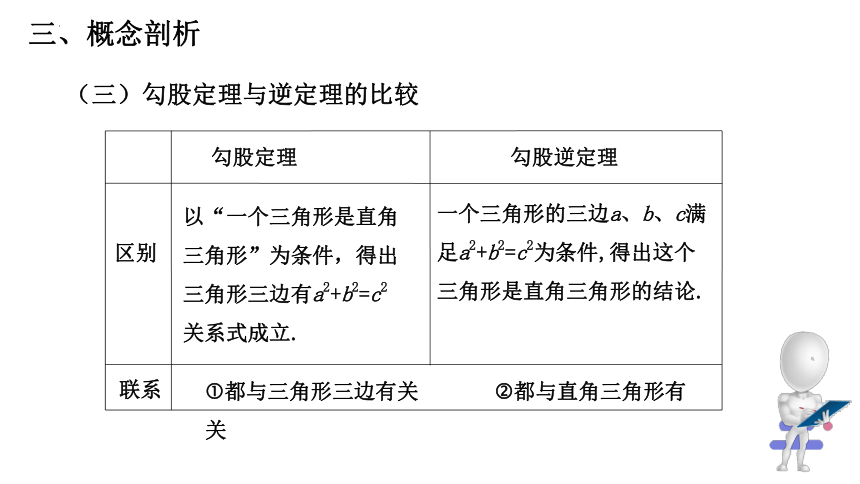
(三)勾股定理与逆定理的比较
以“一个三角形是直角三角形”为条件,得出三角形三边有a2+b2=c2
关系式成立.
一个三角形的三边a、b、c满足a2+b2=c2为条件,得出这个
三角形是直角三角形的结论.
都与三角形三边有关 都与直角三角形有关
勾股定理
勾股逆定理
区别
联系
四、典型例题
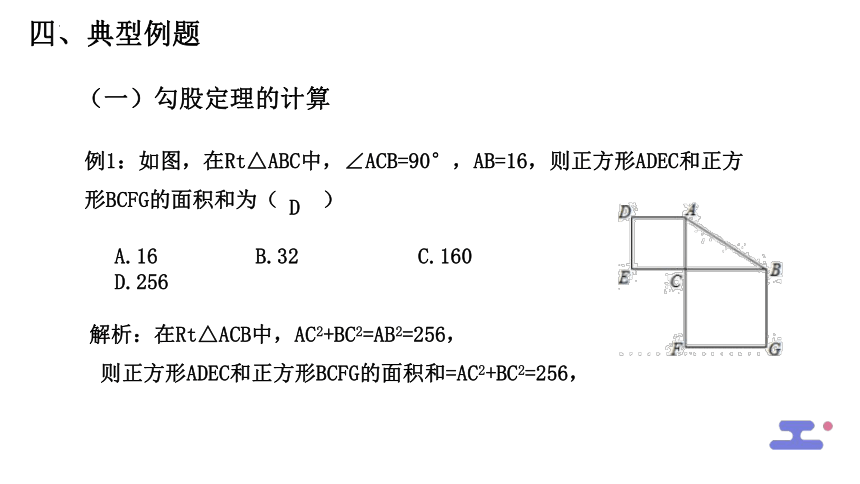
例1:如图,在Rt△ABC中,∠ACB=90°,AB=16,则正方形ADEC和正方形BCFG的面积和为( )
(一)勾股定理的计算
A.16 B.32 C.160 D.256
解析:在Rt△ACB中,AC2+BC2=AB2=256,
则正方形ADEC和正方形BCFG的面积和=AC2+BC2=256,
D
【当堂检测】
1.某直角三角形的一直角边长为8,另一直角边长与斜边长的和为32,则斜边的长为( )
A. 8 B. 10 C. 15 D. 17
解析:设直角三角形的斜边长为x,
由勾股定理得,x2=82+(32-x)2,
解得,x=17,
D
四、典型例题
(二)勾股定理的验证
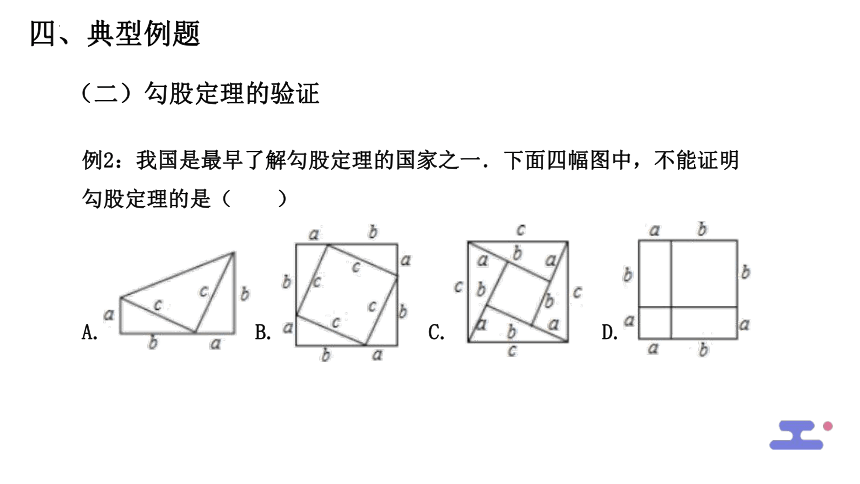
例2:我国是最早了解勾股定理的国家之一.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
四、典型例题
解析:A ab+ c2+ ab= (a+b)(a+b),
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
B、∵4× ab+c2=(a+b)2,
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
C、∵4× ab+(b-a)2=c2,
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
D、根据图形不能证明勾股定理,故本选项符合题意;故选D.
A. B. C. D.
四、典型例题
(三)勾股定理逆定理
例3:如图,在4×4的正方形网格中,每个小正方形的边长都是1.线段AB,AE分别是图中两个1×3的长方形的对角线,请你说明:AB⊥AE.
解:如图,连接BE.
因为AE2=12+32=10,AB2=12+32=10,
BE2=22+42=20,所以AE2+AB2=BE2.
所以△ABE是直角三角形,且∠BAE=90°,
即AB⊥AE.
【当堂检测】
2.有下面的判断:
①若△ABC中,a2+b2≠c2,则△ABC不是直角三角形;
②△ABC是直角三角形,∠C=90°,则a2+b2=c2;
③若△ABC中,a2-b2=c2,则△ABC是直角三角形;
④若△ABC是直角三角形,则(a+b)(a-b)=c2.
其中判断正确的有___________.
② ③
四、典型例题
例4:葛藤是一种多年生草本植物,为获得更多的雨露和阳光,其茎蔓常绕着附近的树干沿最短路线盘旋而上,如果把树干看成圆柱体,它的底面周长是12cm,当一段葛藤绕树干盘旋1圈升高9cm时,这段葛藤的长是多少?
(四)最短路径问题
A
B
解:如图所示:由题意可得,
展开图中AB=12cm,BC=9cm,
则在Rt△ABC中,
AC2=AB2+BC2=122+92=152
答:这段葛藤的长是15cm
A
B
A'
B'
四、典型例题
【当堂检测】
3.一根长90cm的灯管上,缠满了彩色丝带,已知可近似地将灯管看做圆柱体,且底面周长为4cm,彩色丝带均匀地缠绕了30圈,问:丝带共有多长?
A
B
D
C
解:如图所示:
由题意可得,展开图中CD=90cm
∵彩带缠绕了30圈,且底面周长为4cm
∴AD=30×4=120cm
∴AC2=AD2+CD2=902+1202=1502
答:丝带共有150cm.
四、典型例题
(五)运用勾股定理及其逆定理解决问题
例5:在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围半径250米范围内不得进入,问:在进行爆破时,公路AB段是否有危险?是否需要暂时封锁?请用你学过的知识加以解答.
解:如图,过C作CD⊥AB于D.
因为BC=400米,AC=300米,∠ACB=90°,
所以根据勾股定理有AB2=AC2+AB2=5002.
因为S△ABC= AB·CD= BC·AC
所以CD= = =240(米).
由于240米<250米,故有危险,
因此AB段公路需要暂时封锁.
D
四、典型例题
【当堂检测】
4.为修建高速铁路需凿通隧道AC,测得∠BAC=50°,∠B=40°,AB=15km,BC=12km,若每天可凿隧道0.3km,需要几天才能把隧道AC凿通?
解:∵∠A=50°,∠B=40°,
∴∠C=90°.
∵AB=15km,BC=12km,
∴AC2=AB2 BC2=152 122=92
∴ =30(天)
答:需要30天才能将隧道凿通.
【当堂检测】
5.如图,已知某开发区有一块四边形空地ABCD,现计划在该空地上种植草皮,经测量∠ADC=90°,CD=6m,AD=8m,BC=24cm,AB=26m,
若每平方米草皮需200元,则在该空地上种植草皮共需多少钱?
【当堂检测】
解:连接AC,
在Rt△ACD中,AC2=CD2+AD2=62+82=102,
在△ABC中,AB2=262,BC2=242,
而102+242=262,即AC2+BC2=AB2,
∴∠ACB=90°,
S 四边形ABCD=S△ACB-S△ACD= AC BC﹣ AD CD,
= ×10×24﹣ ×8×6 = 96.
所以需费用96×200=19200(元).
五、课堂总结
探索勾股定理
勾股定理的应用
勾股定理
一定是直角三角形吗
验证方法:测量,数格子算面积,割补验证
勾股定理的内容
直角三角形的判别条件:如果三角形的边长a,b,c满足a2+b2=c2
勾股数:满足a2+b2=c2的三个正整数
立体图形表面上两点之间的最短距离
用勾股定理及其逆定理解决实际问题
第一章 勾股定理
复习课
2.能把简单的立体图形转化为平面图形,构造直角三角形求线段长.
一、学习目标
1.知道勾股定理及其逆定理,并会灵活运用解决简单的几何问题和生活实际问题.
二、知识结构
探索勾股定理
勾股定理的应用
勾股定理
一定是直角三角形吗
勾股定理内容及验证验证方法
勾股定理逆定理
三、概念剖析
(一)勾股定理
勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用a、b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2 .
勾股定理的验证:可以采用测量、数格子、割补法,通过构造几何图形,并计算图形面积得出一个等式,从而验证勾股定理.
三、概念剖析
(二)勾股定理逆定理
勾股定理逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
勾股数:满足a2+b2=c2的三个正整数,称为勾股数.
勾股定理逆定理是用来判断一个三角形是否是直角三角形,应用时首先确定该三角形的最大边,当其余两边的平方和等于最大边的平方时,该三角形才是直角三角形.
三、概念剖析
(三)勾股定理与逆定理的比较
以“一个三角形是直角三角形”为条件,得出三角形三边有a2+b2=c2
关系式成立.
一个三角形的三边a、b、c满足a2+b2=c2为条件,得出这个
三角形是直角三角形的结论.
都与三角形三边有关 都与直角三角形有关
勾股定理
勾股逆定理
区别
联系
四、典型例题
例1:如图,在Rt△ABC中,∠ACB=90°,AB=16,则正方形ADEC和正方形BCFG的面积和为( )
(一)勾股定理的计算
A.16 B.32 C.160 D.256
解析:在Rt△ACB中,AC2+BC2=AB2=256,
则正方形ADEC和正方形BCFG的面积和=AC2+BC2=256,
D
【当堂检测】
1.某直角三角形的一直角边长为8,另一直角边长与斜边长的和为32,则斜边的长为( )
A. 8 B. 10 C. 15 D. 17
解析:设直角三角形的斜边长为x,
由勾股定理得,x2=82+(32-x)2,
解得,x=17,
D
四、典型例题
(二)勾股定理的验证
例2:我国是最早了解勾股定理的国家之一.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
四、典型例题
解析:A ab+ c2+ ab= (a+b)(a+b),
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
B、∵4× ab+c2=(a+b)2,
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
C、∵4× ab+(b-a)2=c2,
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
D、根据图形不能证明勾股定理,故本选项符合题意;故选D.
A. B. C. D.
四、典型例题
(三)勾股定理逆定理
例3:如图,在4×4的正方形网格中,每个小正方形的边长都是1.线段AB,AE分别是图中两个1×3的长方形的对角线,请你说明:AB⊥AE.
解:如图,连接BE.
因为AE2=12+32=10,AB2=12+32=10,
BE2=22+42=20,所以AE2+AB2=BE2.
所以△ABE是直角三角形,且∠BAE=90°,
即AB⊥AE.
【当堂检测】
2.有下面的判断:
①若△ABC中,a2+b2≠c2,则△ABC不是直角三角形;
②△ABC是直角三角形,∠C=90°,则a2+b2=c2;
③若△ABC中,a2-b2=c2,则△ABC是直角三角形;
④若△ABC是直角三角形,则(a+b)(a-b)=c2.
其中判断正确的有___________.
② ③
四、典型例题
例4:葛藤是一种多年生草本植物,为获得更多的雨露和阳光,其茎蔓常绕着附近的树干沿最短路线盘旋而上,如果把树干看成圆柱体,它的底面周长是12cm,当一段葛藤绕树干盘旋1圈升高9cm时,这段葛藤的长是多少?
(四)最短路径问题
A
B
解:如图所示:由题意可得,
展开图中AB=12cm,BC=9cm,
则在Rt△ABC中,
AC2=AB2+BC2=122+92=152
答:这段葛藤的长是15cm
A
B
A'
B'
四、典型例题
【当堂检测】
3.一根长90cm的灯管上,缠满了彩色丝带,已知可近似地将灯管看做圆柱体,且底面周长为4cm,彩色丝带均匀地缠绕了30圈,问:丝带共有多长?
A
B
D
C
解:如图所示:
由题意可得,展开图中CD=90cm
∵彩带缠绕了30圈,且底面周长为4cm
∴AD=30×4=120cm
∴AC2=AD2+CD2=902+1202=1502
答:丝带共有150cm.
四、典型例题
(五)运用勾股定理及其逆定理解决问题
例5:在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围半径250米范围内不得进入,问:在进行爆破时,公路AB段是否有危险?是否需要暂时封锁?请用你学过的知识加以解答.
解:如图,过C作CD⊥AB于D.
因为BC=400米,AC=300米,∠ACB=90°,
所以根据勾股定理有AB2=AC2+AB2=5002.
因为S△ABC= AB·CD= BC·AC
所以CD= = =240(米).
由于240米<250米,故有危险,
因此AB段公路需要暂时封锁.
D
四、典型例题
【当堂检测】
4.为修建高速铁路需凿通隧道AC,测得∠BAC=50°,∠B=40°,AB=15km,BC=12km,若每天可凿隧道0.3km,需要几天才能把隧道AC凿通?
解:∵∠A=50°,∠B=40°,
∴∠C=90°.
∵AB=15km,BC=12km,
∴AC2=AB2 BC2=152 122=92
∴ =30(天)
答:需要30天才能将隧道凿通.
【当堂检测】
5.如图,已知某开发区有一块四边形空地ABCD,现计划在该空地上种植草皮,经测量∠ADC=90°,CD=6m,AD=8m,BC=24cm,AB=26m,
若每平方米草皮需200元,则在该空地上种植草皮共需多少钱?
【当堂检测】
解:连接AC,
在Rt△ACD中,AC2=CD2+AD2=62+82=102,
在△ABC中,AB2=262,BC2=242,
而102+242=262,即AC2+BC2=AB2,
∴∠ACB=90°,
S 四边形ABCD=S△ACB-S△ACD= AC BC﹣ AD CD,
= ×10×24﹣ ×8×6 = 96.
所以需费用96×200=19200(元).
五、课堂总结
探索勾股定理
勾股定理的应用
勾股定理
一定是直角三角形吗
验证方法:测量,数格子算面积,割补验证
勾股定理的内容
直角三角形的判别条件:如果三角形的边长a,b,c满足a2+b2=c2
勾股数:满足a2+b2=c2的三个正整数
立体图形表面上两点之间的最短距离
用勾股定理及其逆定理解决实际问题
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
