北师大版九年级上册数学 4.7 相似三角形的性质 第1课时课件(共13张PPT)
文档属性
| 名称 | 北师大版九年级上册数学 4.7 相似三角形的性质 第1课时课件(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 10:12:38 | ||
图片预览





文档简介
(共13张PPT)
4.7 相似三角形的性质
第1课时
第四章 图形的相似
1.了解相似三角形中对应线段与相似比的关系.
2.能运用相似三角形的性质解决相关问题.
活动:小组合作讨论,完成下列问题.
问题1:如图,小王依据图纸上的△ABC,以1:2的比例建造了模型房梁△A'B'C',CD和C’D’分别是它们的立柱.
(1)△ACD与△A'C'D'相似吗?为什么?如果相似,指出它们的相似比.
(2)如果CD=1.5cm,那么模型房的房梁立柱有多高?
任务一:了解相似三角形中对应线段与相似比的关系
解:(1)∵△ACD∽△A'C'D',理由是∠A=∠A',∠BAD=∠B'A'C'=90°.相似比是1:2.
(2)由CD:C'D'=1:2,得C'D'=2CD=3cm,
即模型房的房梁立柱高3cm.
问题2:如图,△ABC ∽△A'B'C',相似比为k,它们对应高的比是多少?
A
B
C
A'
B'
C'
D
D'
∵△ABC∽△A'B'C',∴∠B=∠B',
解:分别作△ABC和△A'B'C'的高AD和A'D',
则∠ADB=∠A'D'B'=90°.
∴△ABD∽△A'B'D' ,
思考:把上图中的高改为中线、角平分线,那么它们对应中线的比,对应角平分线的比等于多少?
活动探究
学习目标
当堂检测
课堂总结
已知:△ABC∽△A′B′C′,相似比为k,即 ,AD、A′D′分别为对应边上的中线.求证:
证明:∵ △ABC∽△A′B′C′.
∴ ∠B′= ∠B, .
又AD,AD′分别为对应边的中线.
∴ △ABD∽△A′B′D′.
A'
B'
D'
C'
A
B
C
D
验证猜想1
活动探究
学习目标
当堂检测
课堂总结
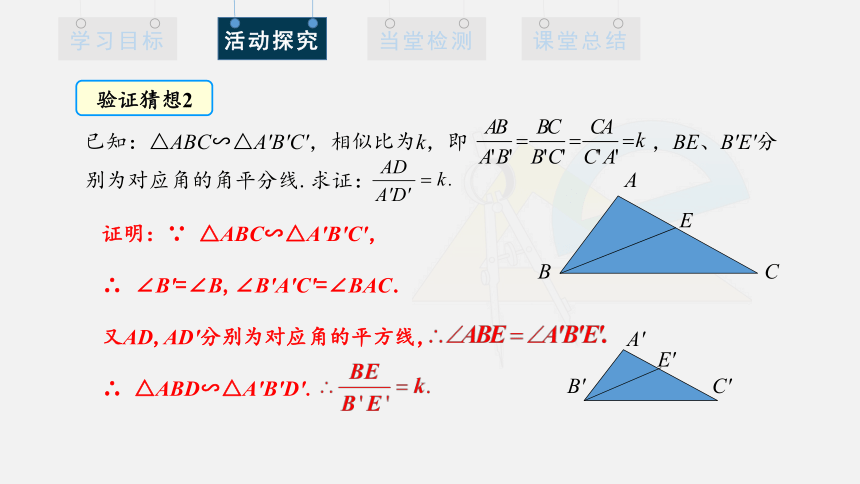
已知:△ABC∽△A′B′C′,相似比为k,即 ,BE、B′E′分别为对应角的角平分线.求证:
A'
B'
C'
E'
A
B
C
E
验证猜想2
证明:∵ △ABC∽△A′B′C′,
∴ ∠B′=∠B,∠B′A′C′=∠BAC.
又AD,AD′分别为对应角的平方线,
∴ △ABD∽△A′B′D′.
归纳总结
相似三角形对应高的比、对应角平分线的比、对应中线的比
都等于相似比.
活动:运用相似三角形的性质完成下列问题.
两个相似三角形的对应边的高分别是6cm和8cm,如果它们对应的两条中线与两条角平分线的和为70cm,中线和与角平分线和的比为2:3,求这两条对应中线的长分别是多少?
任务二:能运用相似三角形的性质解决相关问题
解:设较长的中线长为x cm,
∵中线和+角平分线和=70cm,中线和:角平分线和=2:3.
∴中线和为28cm,
∴较短的中线长为(28-x)cm,
∵两个三角形相似,
解得:x=16,28-x=12,
答:这两条对应中线长分别为12cm、16cm.
1.ΔABC∽ΔA1B1C1 ,BD和B1D1是它们的中线,已知AC是A1C1的1.5倍,
B1D1=4cm,则BD= cm.
2.ΔABC∽ΔA1B1C1, AD和A1D1是对应角平分线,已知AD=8cm, A1D1=2cm ,则ΔABC与ΔA1B1C1的对应高之比为 .
活动探究
学习目标
当堂检测
课堂总结
练一练
6
4
1.ΔABC∽ ΔA1B1C1, AD和A1D1是对应角平分线,已知AD=8cm, A1D1=3cm ,则 ΔABC与ΔA1B1C1的对应高之比为 .
8:3
2.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=4m,点P到CD的距离是3m,则P到AB的距离是 m.
1.5
P
A
D
B
C
2
4
A
G
B
C
D
E
F
H
解:∵ △ABC∽△DEF,
,
解得EH=3.2(cm).
答:EH的长为3.2cm.
3.已知△ABC∽△DEF,BG、EH分△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
针对本节课所学内容,说说你都学到了哪些知识?
相似三角形的性质
相似三角形对应高的比等于相似比
相似三角形对应角平分线的比等于相似比
相似三角形对应中线的比等于相似比
4.7 相似三角形的性质
第1课时
第四章 图形的相似
1.了解相似三角形中对应线段与相似比的关系.
2.能运用相似三角形的性质解决相关问题.
活动:小组合作讨论,完成下列问题.
问题1:如图,小王依据图纸上的△ABC,以1:2的比例建造了模型房梁△A'B'C',CD和C’D’分别是它们的立柱.
(1)△ACD与△A'C'D'相似吗?为什么?如果相似,指出它们的相似比.
(2)如果CD=1.5cm,那么模型房的房梁立柱有多高?
任务一:了解相似三角形中对应线段与相似比的关系
解:(1)∵△ACD∽△A'C'D',理由是∠A=∠A',∠BAD=∠B'A'C'=90°.相似比是1:2.
(2)由CD:C'D'=1:2,得C'D'=2CD=3cm,
即模型房的房梁立柱高3cm.
问题2:如图,△ABC ∽△A'B'C',相似比为k,它们对应高的比是多少?
A
B
C
A'
B'
C'
D
D'
∵△ABC∽△A'B'C',∴∠B=∠B',
解:分别作△ABC和△A'B'C'的高AD和A'D',
则∠ADB=∠A'D'B'=90°.
∴△ABD∽△A'B'D' ,
思考:把上图中的高改为中线、角平分线,那么它们对应中线的比,对应角平分线的比等于多少?
活动探究
学习目标
当堂检测
课堂总结
已知:△ABC∽△A′B′C′,相似比为k,即 ,AD、A′D′分别为对应边上的中线.求证:
证明:∵ △ABC∽△A′B′C′.
∴ ∠B′= ∠B, .
又AD,AD′分别为对应边的中线.
∴ △ABD∽△A′B′D′.
A'
B'
D'
C'
A
B
C
D
验证猜想1
活动探究
学习目标
当堂检测
课堂总结
已知:△ABC∽△A′B′C′,相似比为k,即 ,BE、B′E′分别为对应角的角平分线.求证:
A'
B'
C'
E'
A
B
C
E
验证猜想2
证明:∵ △ABC∽△A′B′C′,
∴ ∠B′=∠B,∠B′A′C′=∠BAC.
又AD,AD′分别为对应角的平方线,
∴ △ABD∽△A′B′D′.
归纳总结
相似三角形对应高的比、对应角平分线的比、对应中线的比
都等于相似比.
活动:运用相似三角形的性质完成下列问题.
两个相似三角形的对应边的高分别是6cm和8cm,如果它们对应的两条中线与两条角平分线的和为70cm,中线和与角平分线和的比为2:3,求这两条对应中线的长分别是多少?
任务二:能运用相似三角形的性质解决相关问题
解:设较长的中线长为x cm,
∵中线和+角平分线和=70cm,中线和:角平分线和=2:3.
∴中线和为28cm,
∴较短的中线长为(28-x)cm,
∵两个三角形相似,
解得:x=16,28-x=12,
答:这两条对应中线长分别为12cm、16cm.
1.ΔABC∽ΔA1B1C1 ,BD和B1D1是它们的中线,已知AC是A1C1的1.5倍,
B1D1=4cm,则BD= cm.
2.ΔABC∽ΔA1B1C1, AD和A1D1是对应角平分线,已知AD=8cm, A1D1=2cm ,则ΔABC与ΔA1B1C1的对应高之比为 .
活动探究
学习目标
当堂检测
课堂总结
练一练
6
4
1.ΔABC∽ ΔA1B1C1, AD和A1D1是对应角平分线,已知AD=8cm, A1D1=3cm ,则 ΔABC与ΔA1B1C1的对应高之比为 .
8:3
2.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=4m,点P到CD的距离是3m,则P到AB的距离是 m.
1.5
P
A
D
B
C
2
4
A
G
B
C
D
E
F
H
解:∵ △ABC∽△DEF,
,
解得EH=3.2(cm).
答:EH的长为3.2cm.
3.已知△ABC∽△DEF,BG、EH分△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
针对本节课所学内容,说说你都学到了哪些知识?
相似三角形的性质
相似三角形对应高的比等于相似比
相似三角形对应角平分线的比等于相似比
相似三角形对应中线的比等于相似比
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
