北师大版数学八年级上册 第三章 位置与坐标 复习 课件 (共30张PPT)
文档属性
| 名称 | 北师大版数学八年级上册 第三章 位置与坐标 复习 课件 (共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 343.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 10:18:49 | ||
图片预览







文档简介
(共30张PPT)
第三章 位置与坐标
复习课
1.能灵活运用不同的方式确定物体位置.
2.进一步加深对平面直角坐标系的理解,在给定的直角坐标系中描出点的位置,由点的位置写出点的坐标,能正确应用坐标变化与图形变换的关系解决问题.
3.能够建立恰当的直角坐标系,描述物体的位置.
一、学习目标
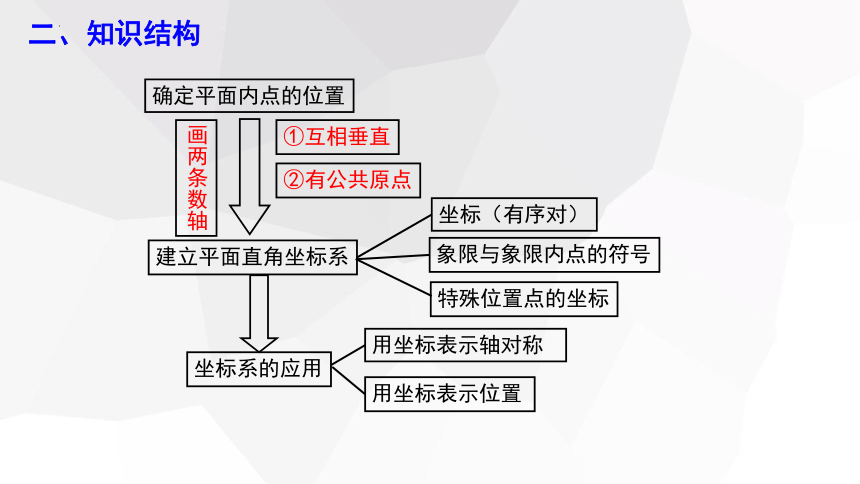
二、知识结构
确定平面内点的位置
①互相垂直
②有公共原点
建立平面直角坐标系
象限与象限内点的符号
特殊位置点的坐标
坐标系的应用
画两条数轴
坐标(有序对)
用坐标表示位置
用坐标表示轴对称
三、知识梳理
(一)物体位置的确定
在平面内,确定物体位置一般需要 个数据.
物体位置确定的方法:有序对、区域法、经纬度、方位法等.
2
三、知识梳理
(二)平面直角坐标系
1.在平面内,两条_________且有_________的_______组成平面直角坐标系.通常,两条数轴分别置于_______位置与_______位置,取_______与_______的方向分别为两条数轴的正方向._______的数轴叫做x轴或横轴,_______的数轴叫做y轴或纵轴,x轴和y轴统称_______,它们的公共原点O称为直角坐标系的_______.
相互垂直
公共原点
数轴
水平
铅直
向右
向上
水平
铅直
坐标轴
原点
三、知识梳理
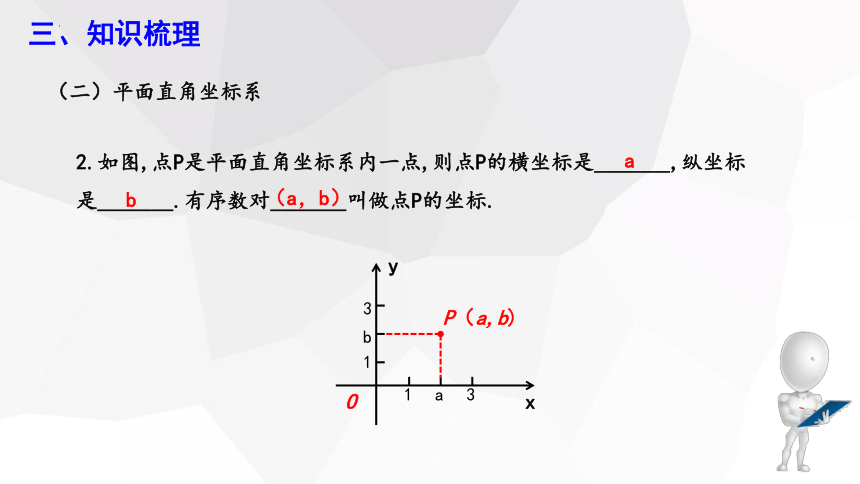
(二)平面直角坐标系
2.如图,点P是平面直角坐标系内一点,则点P的横坐标是_______,纵坐标是_______.有序数对_______叫做点P的坐标.
1
a
3
1
b
3
O
x
y
P(a,b)
a
b
(a,b)
三、知识梳理
(二)平面直角坐标系
3.在平面直角坐标系中,两条坐标轴将平面分成了四个象限,请在图中标出各象限的名称,并在括号内写出这个象限的符号特征.
第一象限
+ +
第二象限
- +
第三象限
- -
第四象限
+ -
三、知识梳理
(二)平面直角坐标系
4.坐标轴上的点_______(填“在”或“不在”)任何一个象限内.
5.x轴上的点的_____坐标为0;y轴上的点的______坐标为0.
6.平行于x轴的直线上各点的_____坐标相同;平行于y轴的直线上各点的_____坐标相同.
不在
纵
横
纵
横
三、知识梳理
(三)点的变化与轴对称
在直角坐标系内,关于x轴对称的两个点的坐标,横坐标______,纵坐标___________;
关于y轴对称的两个点的坐标,纵坐标______,横坐标__________.
相同
互为相反数
相同
互为相反数
四、典型例题
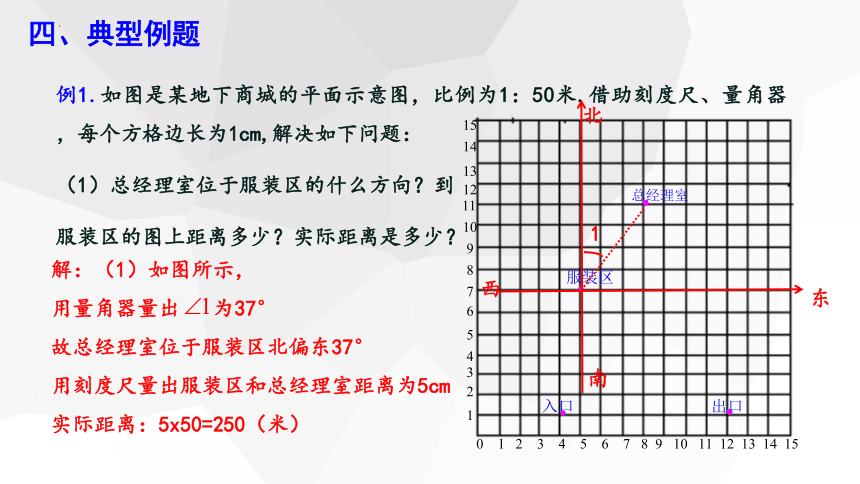
例1.如图是某地下商城的平面示意图,比例为1:50米.借助刻度尺、量角器,每个方格边长为1cm,解决如下问题:
(1)总经理室位于服装区的什么方向?到
服装区的图上距离多少?实际距离是多少?
总经理室
.
.
.
.
出口
入口
服装区
8
7
6
5
4
3
2
1
13
11
12
9
10
15
14
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
解:(1)如图所示,
用量角器量出 为37°
故总经理室位于服装区北偏东37°
用刻度尺量出服装区和总经理室距离为5cm
实际距离:5x50=250(米)
东
北
西
南
1
四、典型例题
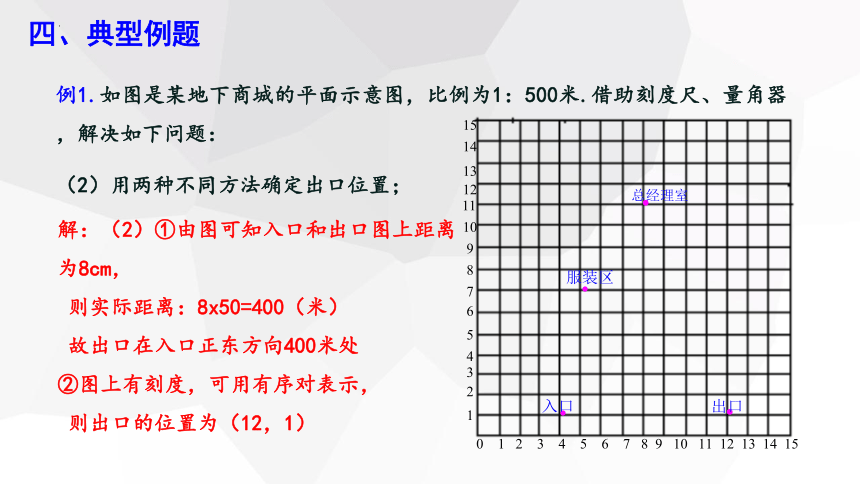
例1.如图是某地下商城的平面示意图,比例为1:500米.借助刻度尺、量角器,解决如下问题:
(2)用两种不同方法确定出口位置;
总经理室
.
.
.
.
出口
入口
服装区
8
7
6
5
4
3
2
1
13
11
12
9
10
15
14
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
解:(2)①由图可知入口和出口图上距离为8cm,
则实际距离:8x50=400(米)
故出口在入口正东方向400米处
②图上有刻度,可用有序对表示,
则出口的位置为(12,1)
四、典型例题
例1.如图是某地下商城的平面示意图,比例为1:500米.借助刻度尺、量角器,解决如下问题:
(3)确定服装区的位置.
总经理室
.
.
.
.
出口
入口
服装区
8
7
6
5
4
3
2
1
13
11
12
9
10
15
14
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
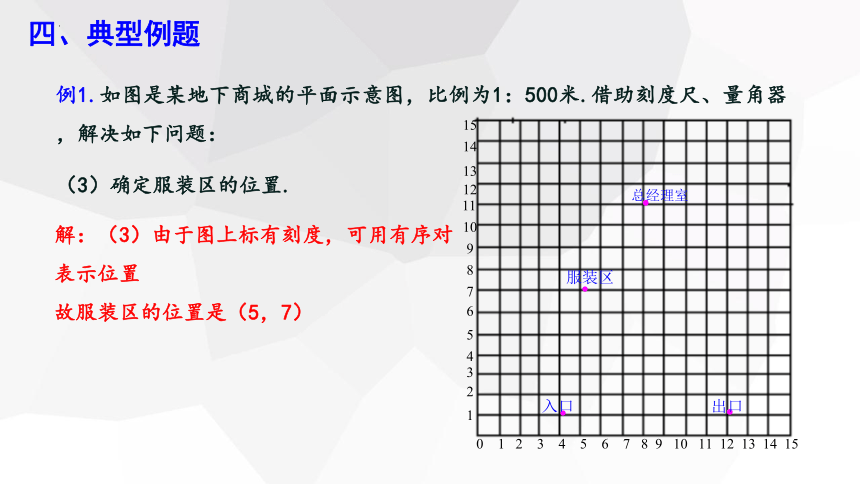
解:(3)由于图上标有刻度,可用有序对表示位置
故服装区的位置是(5,7)
【当堂检测】
1.在平面内,下列数据能否确定物体位置;不能的话修改正确.
电影院2号厅4排
解放路
东经120°,北纬30°
北偏西40°
不能,改为4排8号(答案不唯一)
不能,改为解放路一街(答案不唯一)
不能,改为北偏西40°200米 (答案不唯一)
能
排号和座位号
区域法:区域和区域
经纬度:经度和纬度
方位法:方位角和距离
四、典型例题
例2.如图是某市市区几个旅游景点的平面示意图,(1)选取某一景点为坐标原点,建立平面直角坐标系;(2)在所建立的平面直角坐标系中,写出其余各景点的坐标。
动物园
山陕会馆
金凤广场
光岳楼
湖心岛
四、典型例题
解:(1)以金凤广场为坐标原点,如图:
动物园
山陕会馆
金凤广场
光岳楼
湖心岛
x
y
(2)湖心岛的坐标为(1,4);
光岳楼的坐标为(2,2);
山陕会馆的坐标为(4,1);
动物园的坐标为(6,6).
【当堂检测】
2.中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(0,-2),“马”位于点(4,-2),则“兵”位于点 .
(-1,1)
分析:如图所示,可得原点位置,则“兵”位于点(-1,1).
x
y
O
【当堂检测】
3.如图,在正方形网格中,若A(0,1),B(1,0),则点C的坐标为( )
A.(-2,2) B.(3,-2)
C.(-2,-2) D.(2,-2)
D
【当堂检测】
4.在平面直角坐标系中有A、B两点,若以B点为原点建立直角坐标系,则A点的坐标为(2,3);若以A点为原点建立直角坐标系(两直角坐标系x轴、y轴方向一致),则B点的坐标是( )
A.(-2,-3) B.(-2,3)
C.(2,-3) D.(2,3)
A
x
y
A
B
x
y
分析:如图所示
四、典型例题
例3.在平面直角坐标系中,已知点M(m,2m+3).
(1)若点M在x轴上,求m的值;
解:∵点M在x轴上,
∴2m+3=0,
解得:m=-1.5
四、典型例题
例3.在平面直角坐标系中,已知点M(m,2m+3).
(2)若点M在第二象限内,已知点M到x轴的距离为1,求点M的坐标;
解:∵点M在第二象限内,
∴点M的坐标为(-,+)
又∵点M到x轴的距离为1,
∴2m+3=1,解得m=-1,
∴点M的坐标为(-1,1)
四、典型例题
例3.在平面直角坐标系中,已知点M(m,2m+3).
(3)点N(4,5),若线段MN平行于y轴,求点M的坐标.
解:∵线段MN平行于y轴
∴点N与点M的横坐标相同
∴m=4
则2m+3=11,
∴点M的坐标为(4,11)
【当堂检测】
4.在x轴上的点P到y轴的距离为3,则点P的坐标为( )
A.(3,0) C.(3,0)或(-3,0)
B.(0,3) D.(0,3)或(0,-3)
分析:∵点P在x轴上
∴P的坐标为(a,0),
由题可知:|a|=3
∴a=3或-3
故P的坐标为(3,0)或(-3,0)
B
易错点:只写一个坐标
【当堂检测】
5.给出下列四个命题:
(1)坐标平面内的点与有序实数对一一对应;
(2)若a>0,b不大于0,则P(-a,b)在第三象限内;
(3)在x轴上的点纵坐标都为0;
(4)当m不为0时,P(m,-m)在第四象限内.
其中说法正确的是 .
(1)、(3)
点P只能确定横坐标-a为负,
故在第三象限或x轴上
点P横、纵坐标异号,根据象限内点坐标特点可知:点P在第二或第四象限
【当堂检测】
6.已知线段MN=4,MN平行于y轴,若点M的坐标为(-1,2),求点N的坐标.
解:MN平行于y轴,则点M与点N的横坐标相同,
即:N的坐标为(-1,y)
所以MN的长度为点M与点N的纵坐标的差的绝对值
点N有两种情况:在点M的正上方或正下方
在点M的正上方,则MN=4=y-2,可得:y=6,此时点N的坐标为(-1,6)
在点M的正下方,则MN=4=2-y,可得:y=-2,此时点N的坐标为(-1,-2)
综上所述:点N的坐标为(-1,-2)或(-1,6)
易错点:只考虑一种情况
四、典型例题
例4.将图中的点(3,0),(7,0),(2,2)(3,2),(7,2),(8,2),(5,4)做如下变化,画出图形,说说变化前后图形的关系.
(1)纵坐标不变,横坐标分别乘以-1.
解:(1)坐标变化如下表,
根据坐标描出对应点,并依次连线
结果如图.
所得图形与原图形关于y轴对称
2 3 4 5 6 7 8
3
2
4
5
变化前 (3,0) (7,0) (2,2) (3,2) (7,2) (8,2) (5,4)
变化后 (-3,0) (-7,0) (-2,2) (-3,2) (-7,2) (-8,2) (-5,4)
-8
-7
-3
-6
-5
-4
-2
-1
关于y轴对称的点的坐标:
纵坐标相同,横坐标互为相反数
四、典型例题
例4.将图中的点(3,0),(7,0),(2,2)(3,2),(7,2),(8,2),(5,4)做如下变化,画出图形,说说变化前后图形的关系.
(2)横坐标不变,纵坐标分别乘以-1.
2 3 4 5 6 7 8
3
2
4
5
解:(1)坐标变化如下表,
根据坐标描出对应点,并依次连线
结果如图.
所得图形与原图形关于x轴对称
变化前 (3,0) (7,0) (2,2) (3,2) (7,2) (8,2) (5,4)
变化后 (3,0) (7,0) (2,-2) (3,-2) (7,-2) (8,-2) (5,-4)
-1
-2
-3
-4
关于x轴对称的点的坐标:
横坐标相同,纵坐标互为相反数
【当堂检测】
7.点A(-3,2a)关于x轴对称点P的坐标是(3b,4),则a= ,b= .
分析:∵点A和点P关于x轴对称
∴-3=3b,2a=-4
(关于x轴对称的点的横坐标相同,纵坐标互为相反数)
可得:a=-2,b=-1
-2
-1
【当堂检测】
8.△ABC与△DEF在平面直角坐标系中的位置如图
若点P(m,n)是△ABC内部一点,则在△DEF内的对应点P'的坐标为 .
(-m,n)
分析:由图可知,两个三角形关于y轴对称,即:对应点关于y轴对称
五、课堂总结
1.平面内确定物体的位置,一般需要2个数据;生活中确定位置的方法有方位法、有序对、经纬度、区域法等.
2.一个平面直角坐标系有四个象限,其点的坐标特点:
第一象限(+,+),第二象限(-,+)
第三象限(-,-),第四象限(+,-)
3.坐标轴上的点不属于任何象限,其坐标特点:
x轴上(a,0),y轴上(0,b)(其中a,b均为不为0的任何数)
五、课堂总结
4.平行于x轴的线上的点:横坐标不同,纵坐标相同
平行于y轴的线上的点:横坐标相同,纵坐标不同
5.关于x轴对称的点的坐标:横坐标相同,纵坐标互为相反数
关于y轴对称的点的坐标:横坐标互为相反数,纵坐标相同
第三章 位置与坐标
复习课
1.能灵活运用不同的方式确定物体位置.
2.进一步加深对平面直角坐标系的理解,在给定的直角坐标系中描出点的位置,由点的位置写出点的坐标,能正确应用坐标变化与图形变换的关系解决问题.
3.能够建立恰当的直角坐标系,描述物体的位置.
一、学习目标
二、知识结构
确定平面内点的位置
①互相垂直
②有公共原点
建立平面直角坐标系
象限与象限内点的符号
特殊位置点的坐标
坐标系的应用
画两条数轴
坐标(有序对)
用坐标表示位置
用坐标表示轴对称
三、知识梳理
(一)物体位置的确定
在平面内,确定物体位置一般需要 个数据.
物体位置确定的方法:有序对、区域法、经纬度、方位法等.
2
三、知识梳理
(二)平面直角坐标系
1.在平面内,两条_________且有_________的_______组成平面直角坐标系.通常,两条数轴分别置于_______位置与_______位置,取_______与_______的方向分别为两条数轴的正方向._______的数轴叫做x轴或横轴,_______的数轴叫做y轴或纵轴,x轴和y轴统称_______,它们的公共原点O称为直角坐标系的_______.
相互垂直
公共原点
数轴
水平
铅直
向右
向上
水平
铅直
坐标轴
原点
三、知识梳理
(二)平面直角坐标系
2.如图,点P是平面直角坐标系内一点,则点P的横坐标是_______,纵坐标是_______.有序数对_______叫做点P的坐标.
1
a
3
1
b
3
O
x
y
P(a,b)
a
b
(a,b)
三、知识梳理
(二)平面直角坐标系
3.在平面直角坐标系中,两条坐标轴将平面分成了四个象限,请在图中标出各象限的名称,并在括号内写出这个象限的符号特征.
第一象限
+ +
第二象限
- +
第三象限
- -
第四象限
+ -
三、知识梳理
(二)平面直角坐标系
4.坐标轴上的点_______(填“在”或“不在”)任何一个象限内.
5.x轴上的点的_____坐标为0;y轴上的点的______坐标为0.
6.平行于x轴的直线上各点的_____坐标相同;平行于y轴的直线上各点的_____坐标相同.
不在
纵
横
纵
横
三、知识梳理
(三)点的变化与轴对称
在直角坐标系内,关于x轴对称的两个点的坐标,横坐标______,纵坐标___________;
关于y轴对称的两个点的坐标,纵坐标______,横坐标__________.
相同
互为相反数
相同
互为相反数
四、典型例题
例1.如图是某地下商城的平面示意图,比例为1:50米.借助刻度尺、量角器,每个方格边长为1cm,解决如下问题:
(1)总经理室位于服装区的什么方向?到
服装区的图上距离多少?实际距离是多少?
总经理室
.
.
.
.
出口
入口
服装区
8
7
6
5
4
3
2
1
13
11
12
9
10
15
14
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
解:(1)如图所示,
用量角器量出 为37°
故总经理室位于服装区北偏东37°
用刻度尺量出服装区和总经理室距离为5cm
实际距离:5x50=250(米)
东
北
西
南
1
四、典型例题
例1.如图是某地下商城的平面示意图,比例为1:500米.借助刻度尺、量角器,解决如下问题:
(2)用两种不同方法确定出口位置;
总经理室
.
.
.
.
出口
入口
服装区
8
7
6
5
4
3
2
1
13
11
12
9
10
15
14
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
解:(2)①由图可知入口和出口图上距离为8cm,
则实际距离:8x50=400(米)
故出口在入口正东方向400米处
②图上有刻度,可用有序对表示,
则出口的位置为(12,1)
四、典型例题
例1.如图是某地下商城的平面示意图,比例为1:500米.借助刻度尺、量角器,解决如下问题:
(3)确定服装区的位置.
总经理室
.
.
.
.
出口
入口
服装区
8
7
6
5
4
3
2
1
13
11
12
9
10
15
14
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
解:(3)由于图上标有刻度,可用有序对表示位置
故服装区的位置是(5,7)
【当堂检测】
1.在平面内,下列数据能否确定物体位置;不能的话修改正确.
电影院2号厅4排
解放路
东经120°,北纬30°
北偏西40°
不能,改为4排8号(答案不唯一)
不能,改为解放路一街(答案不唯一)
不能,改为北偏西40°200米 (答案不唯一)
能
排号和座位号
区域法:区域和区域
经纬度:经度和纬度
方位法:方位角和距离
四、典型例题
例2.如图是某市市区几个旅游景点的平面示意图,(1)选取某一景点为坐标原点,建立平面直角坐标系;(2)在所建立的平面直角坐标系中,写出其余各景点的坐标。
动物园
山陕会馆
金凤广场
光岳楼
湖心岛
四、典型例题
解:(1)以金凤广场为坐标原点,如图:
动物园
山陕会馆
金凤广场
光岳楼
湖心岛
x
y
(2)湖心岛的坐标为(1,4);
光岳楼的坐标为(2,2);
山陕会馆的坐标为(4,1);
动物园的坐标为(6,6).
【当堂检测】
2.中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(0,-2),“马”位于点(4,-2),则“兵”位于点 .
(-1,1)
分析:如图所示,可得原点位置,则“兵”位于点(-1,1).
x
y
O
【当堂检测】
3.如图,在正方形网格中,若A(0,1),B(1,0),则点C的坐标为( )
A.(-2,2) B.(3,-2)
C.(-2,-2) D.(2,-2)
D
【当堂检测】
4.在平面直角坐标系中有A、B两点,若以B点为原点建立直角坐标系,则A点的坐标为(2,3);若以A点为原点建立直角坐标系(两直角坐标系x轴、y轴方向一致),则B点的坐标是( )
A.(-2,-3) B.(-2,3)
C.(2,-3) D.(2,3)
A
x
y
A
B
x
y
分析:如图所示
四、典型例题
例3.在平面直角坐标系中,已知点M(m,2m+3).
(1)若点M在x轴上,求m的值;
解:∵点M在x轴上,
∴2m+3=0,
解得:m=-1.5
四、典型例题
例3.在平面直角坐标系中,已知点M(m,2m+3).
(2)若点M在第二象限内,已知点M到x轴的距离为1,求点M的坐标;
解:∵点M在第二象限内,
∴点M的坐标为(-,+)
又∵点M到x轴的距离为1,
∴2m+3=1,解得m=-1,
∴点M的坐标为(-1,1)
四、典型例题
例3.在平面直角坐标系中,已知点M(m,2m+3).
(3)点N(4,5),若线段MN平行于y轴,求点M的坐标.
解:∵线段MN平行于y轴
∴点N与点M的横坐标相同
∴m=4
则2m+3=11,
∴点M的坐标为(4,11)
【当堂检测】
4.在x轴上的点P到y轴的距离为3,则点P的坐标为( )
A.(3,0) C.(3,0)或(-3,0)
B.(0,3) D.(0,3)或(0,-3)
分析:∵点P在x轴上
∴P的坐标为(a,0),
由题可知:|a|=3
∴a=3或-3
故P的坐标为(3,0)或(-3,0)
B
易错点:只写一个坐标
【当堂检测】
5.给出下列四个命题:
(1)坐标平面内的点与有序实数对一一对应;
(2)若a>0,b不大于0,则P(-a,b)在第三象限内;
(3)在x轴上的点纵坐标都为0;
(4)当m不为0时,P(m,-m)在第四象限内.
其中说法正确的是 .
(1)、(3)
点P只能确定横坐标-a为负,
故在第三象限或x轴上
点P横、纵坐标异号,根据象限内点坐标特点可知:点P在第二或第四象限
【当堂检测】
6.已知线段MN=4,MN平行于y轴,若点M的坐标为(-1,2),求点N的坐标.
解:MN平行于y轴,则点M与点N的横坐标相同,
即:N的坐标为(-1,y)
所以MN的长度为点M与点N的纵坐标的差的绝对值
点N有两种情况:在点M的正上方或正下方
在点M的正上方,则MN=4=y-2,可得:y=6,此时点N的坐标为(-1,6)
在点M的正下方,则MN=4=2-y,可得:y=-2,此时点N的坐标为(-1,-2)
综上所述:点N的坐标为(-1,-2)或(-1,6)
易错点:只考虑一种情况
四、典型例题
例4.将图中的点(3,0),(7,0),(2,2)(3,2),(7,2),(8,2),(5,4)做如下变化,画出图形,说说变化前后图形的关系.
(1)纵坐标不变,横坐标分别乘以-1.
解:(1)坐标变化如下表,
根据坐标描出对应点,并依次连线
结果如图.
所得图形与原图形关于y轴对称
2 3 4 5 6 7 8
3
2
4
5
变化前 (3,0) (7,0) (2,2) (3,2) (7,2) (8,2) (5,4)
变化后 (-3,0) (-7,0) (-2,2) (-3,2) (-7,2) (-8,2) (-5,4)
-8
-7
-3
-6
-5
-4
-2
-1
关于y轴对称的点的坐标:
纵坐标相同,横坐标互为相反数
四、典型例题
例4.将图中的点(3,0),(7,0),(2,2)(3,2),(7,2),(8,2),(5,4)做如下变化,画出图形,说说变化前后图形的关系.
(2)横坐标不变,纵坐标分别乘以-1.
2 3 4 5 6 7 8
3
2
4
5
解:(1)坐标变化如下表,
根据坐标描出对应点,并依次连线
结果如图.
所得图形与原图形关于x轴对称
变化前 (3,0) (7,0) (2,2) (3,2) (7,2) (8,2) (5,4)
变化后 (3,0) (7,0) (2,-2) (3,-2) (7,-2) (8,-2) (5,-4)
-1
-2
-3
-4
关于x轴对称的点的坐标:
横坐标相同,纵坐标互为相反数
【当堂检测】
7.点A(-3,2a)关于x轴对称点P的坐标是(3b,4),则a= ,b= .
分析:∵点A和点P关于x轴对称
∴-3=3b,2a=-4
(关于x轴对称的点的横坐标相同,纵坐标互为相反数)
可得:a=-2,b=-1
-2
-1
【当堂检测】
8.△ABC与△DEF在平面直角坐标系中的位置如图
若点P(m,n)是△ABC内部一点,则在△DEF内的对应点P'的坐标为 .
(-m,n)
分析:由图可知,两个三角形关于y轴对称,即:对应点关于y轴对称
五、课堂总结
1.平面内确定物体的位置,一般需要2个数据;生活中确定位置的方法有方位法、有序对、经纬度、区域法等.
2.一个平面直角坐标系有四个象限,其点的坐标特点:
第一象限(+,+),第二象限(-,+)
第三象限(-,-),第四象限(+,-)
3.坐标轴上的点不属于任何象限,其坐标特点:
x轴上(a,0),y轴上(0,b)(其中a,b均为不为0的任何数)
五、课堂总结
4.平行于x轴的线上的点:横坐标不同,纵坐标相同
平行于y轴的线上的点:横坐标相同,纵坐标不同
5.关于x轴对称的点的坐标:横坐标相同,纵坐标互为相反数
关于y轴对称的点的坐标:横坐标互为相反数,纵坐标相同
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
