北师大版八年级上册数学 3.2 平面直角坐标系 第3课时课件 (共16张PPT)
文档属性
| 名称 | 北师大版八年级上册数学 3.2 平面直角坐标系 第3课时课件 (共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 351.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 10:19:34 | ||
图片预览




文档简介
(共16张PPT)
第三章 坐标与位置
3.2 平面直角坐标系
第3课时
1.探究并理解平面直角坐标系及其应用.
2.能够根据图形特点建立适当的坐标系,并能写出各顶点的坐标
一、学习目标
二、新课导入
在一次“寻宝”游戏中,寻宝人已经找到了坐标为(3,2)和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4,4),除此之外不知道其他信息.
如何确定直角坐标系
找到宝藏?
三、典型例题
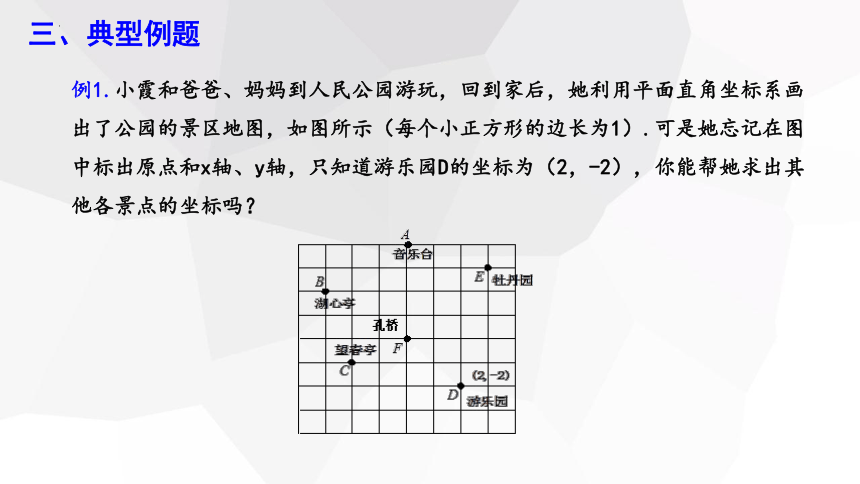
例1.小霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示(每个小正方形的边长为1).可是她忘记在图中标出原点和x轴、y轴,只知道游乐园D的坐标为(2,-2),你能帮她求出其他各景点的坐标吗?
三、典型例题
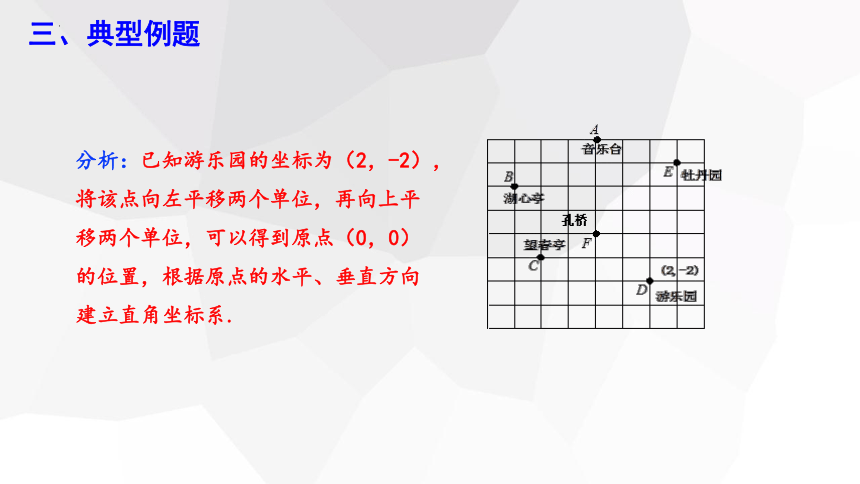
分析:已知游乐园的坐标为(2,-2),将该点向左平移两个单位,再向上平移两个单位,可以得到原点(0,0)的位置,根据原点的水平、垂直方向建立直角坐标系.
三、典型例题
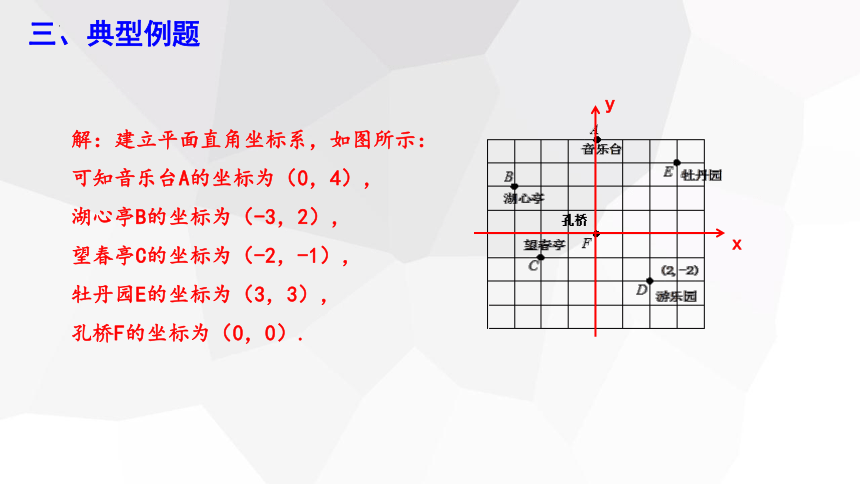
解:建立平面直角坐标系,如图所示:
可知音乐台A的坐标为(0,4),
湖心亭B的坐标为(-3,2),
望春亭C的坐标为(-2,-1),
牡丹园E的坐标为(3,3),
孔桥F的坐标为(0,0).
x
y
【当堂检测】
1.2019年4月29日中国世界园艺博览会在北京延庆开幕,大会以“绿色生活,美丽家园”为主题.如图,是北京世界园艺博览会部分导游图,若国际馆的坐标为(4,2),植物馆的坐标为(-4,-1),则中国馆的坐标为_________.
分析:根据国际馆和植物馆的坐标,确定坐标轴,如图,得出中国馆的坐标为(0,0).
(0,0)
x
y
O
【当堂检测】
2.建立平面直角坐标系,使点C的坐标为(4,0),写出点A、B、D、E、F、G的坐标.
解:如图所示,以B为坐标原点,BC所在直线为x轴,过点B且垂直于x轴的直线为y轴建立平面直角坐标系,则
A(-2,3),B(0,0),D(6,1),
E(5,3),F(3,2),G(1,5).
x
y
【当堂检测】
3.如图,在8×8的方格纸中,△ABC是格点三角形,且A(-2,4),C(0,3).
在8×8的方格纸中建立平面直角坐标系,并求出B点坐标;
解:建立平面直角坐标系如图所示:
点B的坐标为(-4,1)
x
y
三、典型例题
例2.如图,已知在△ABC中,AB=6,AC=BC=5,建立适当的平面直角坐标系,写出△ABC各顶点的坐标.
解:如图,以点A为原点,以AB所在直线为
x轴,过点A垂直于AB的直线为y轴,建立平
面直角坐标系.过点C作CD⊥AB于点D.易知D
为AB的中点.
∵AB=6,∴AD=BD=3,
∴CD=
∴点A的坐标为(0,0),点C的坐标为(3,4),点B的坐标为(6,0).
A
B
C
x
y
D
三、典型例题
归纳总结:
在确定坐标系时,要先看图形的已知条件或给出已知点的位置,同时要看此到坐标轴的距离(必要时做图形的辅助线),进而计算点到坐标轴的距离.
【当堂检测】
4.直角梯形ABCD在直角坐标系中的位置如图,若AD=5,A点的坐标为(-2,7),则D点的坐标为___________.
(3,7)
分析:作DE⊥BC
∵A点的坐标为(-2,5),直角梯形ABCD
∴DE=5,BO=2
∵AD=BE=5,∴OE=3
∵D在第一象限,∴D(3,5)
E
【当堂检测】
5.如图,长方形ABCD的两条边长分别为3、4.请建立一个直角坐标系,使x轴与BC平行,且点C的坐标是(1,-2),并写出其他三点的坐标.
解:建立平面直角坐标系,如右图所示:
x
y
点A的坐标为(-3,1),
B点坐标为(-3,-2),
D点坐标为(1,1).
【当堂检测】
6.解决“寻宝”游戏问题:
寻宝人已经找到了坐标为(3,2)和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4,4),除此之外不知道其他信息.如何确定直角坐标系.
【当堂检测】
6.解决“寻宝”游戏问题:
寻宝人已经找到了坐标为(3,2)和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4,4),除此之外不知道其他信息.如何确定直角坐标系.
解:根据已知两个标志点,建立方格平面直角坐标系,如右图所示:
A(3,2)
B(3,-2)
(4,4)
从而得出藏宝点的位置.
四、课堂总结
平面直角坐标系
能写出各顶点的坐标
能够根据图形特点建立适当的坐标系
第三章 坐标与位置
3.2 平面直角坐标系
第3课时
1.探究并理解平面直角坐标系及其应用.
2.能够根据图形特点建立适当的坐标系,并能写出各顶点的坐标
一、学习目标
二、新课导入
在一次“寻宝”游戏中,寻宝人已经找到了坐标为(3,2)和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4,4),除此之外不知道其他信息.
如何确定直角坐标系
找到宝藏?
三、典型例题
例1.小霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示(每个小正方形的边长为1).可是她忘记在图中标出原点和x轴、y轴,只知道游乐园D的坐标为(2,-2),你能帮她求出其他各景点的坐标吗?
三、典型例题
分析:已知游乐园的坐标为(2,-2),将该点向左平移两个单位,再向上平移两个单位,可以得到原点(0,0)的位置,根据原点的水平、垂直方向建立直角坐标系.
三、典型例题
解:建立平面直角坐标系,如图所示:
可知音乐台A的坐标为(0,4),
湖心亭B的坐标为(-3,2),
望春亭C的坐标为(-2,-1),
牡丹园E的坐标为(3,3),
孔桥F的坐标为(0,0).
x
y
【当堂检测】
1.2019年4月29日中国世界园艺博览会在北京延庆开幕,大会以“绿色生活,美丽家园”为主题.如图,是北京世界园艺博览会部分导游图,若国际馆的坐标为(4,2),植物馆的坐标为(-4,-1),则中国馆的坐标为_________.
分析:根据国际馆和植物馆的坐标,确定坐标轴,如图,得出中国馆的坐标为(0,0).
(0,0)
x
y
O
【当堂检测】
2.建立平面直角坐标系,使点C的坐标为(4,0),写出点A、B、D、E、F、G的坐标.
解:如图所示,以B为坐标原点,BC所在直线为x轴,过点B且垂直于x轴的直线为y轴建立平面直角坐标系,则
A(-2,3),B(0,0),D(6,1),
E(5,3),F(3,2),G(1,5).
x
y
【当堂检测】
3.如图,在8×8的方格纸中,△ABC是格点三角形,且A(-2,4),C(0,3).
在8×8的方格纸中建立平面直角坐标系,并求出B点坐标;
解:建立平面直角坐标系如图所示:
点B的坐标为(-4,1)
x
y
三、典型例题
例2.如图,已知在△ABC中,AB=6,AC=BC=5,建立适当的平面直角坐标系,写出△ABC各顶点的坐标.
解:如图,以点A为原点,以AB所在直线为
x轴,过点A垂直于AB的直线为y轴,建立平
面直角坐标系.过点C作CD⊥AB于点D.易知D
为AB的中点.
∵AB=6,∴AD=BD=3,
∴CD=
∴点A的坐标为(0,0),点C的坐标为(3,4),点B的坐标为(6,0).
A
B
C
x
y
D
三、典型例题
归纳总结:
在确定坐标系时,要先看图形的已知条件或给出已知点的位置,同时要看此到坐标轴的距离(必要时做图形的辅助线),进而计算点到坐标轴的距离.
【当堂检测】
4.直角梯形ABCD在直角坐标系中的位置如图,若AD=5,A点的坐标为(-2,7),则D点的坐标为___________.
(3,7)
分析:作DE⊥BC
∵A点的坐标为(-2,5),直角梯形ABCD
∴DE=5,BO=2
∵AD=BE=5,∴OE=3
∵D在第一象限,∴D(3,5)
E
【当堂检测】
5.如图,长方形ABCD的两条边长分别为3、4.请建立一个直角坐标系,使x轴与BC平行,且点C的坐标是(1,-2),并写出其他三点的坐标.
解:建立平面直角坐标系,如右图所示:
x
y
点A的坐标为(-3,1),
B点坐标为(-3,-2),
D点坐标为(1,1).
【当堂检测】
6.解决“寻宝”游戏问题:
寻宝人已经找到了坐标为(3,2)和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4,4),除此之外不知道其他信息.如何确定直角坐标系.
【当堂检测】
6.解决“寻宝”游戏问题:
寻宝人已经找到了坐标为(3,2)和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4,4),除此之外不知道其他信息.如何确定直角坐标系.
解:根据已知两个标志点,建立方格平面直角坐标系,如右图所示:
A(3,2)
B(3,-2)
(4,4)
从而得出藏宝点的位置.
四、课堂总结
平面直角坐标系
能写出各顶点的坐标
能够根据图形特点建立适当的坐标系
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
