14.3.1提公因式法课件
图片预览







文档简介
课件23张PPT。 14.3提公因式法分解因式教学目标1.初步了解什么叫因式分解?
2. 了解整式乘法与因式分解的区别和联系是什么。
3. 理解什么是公因式?知道如何找公因式。
4. 初步掌握提公因式法。带着以上问题,自学课本仔细阅读课本,完成下列各题1、因式分解:把一个多项式化成几个整式的____的形式叫做把这个多项式因式分解。2、公因式:多项式的各项都含有一个________的因式,我们把这个因式叫做这个多项式的各项的公因式。 3、提公因式法:把多项式各项中的________提取出来,这种分解因式的方法叫做提公因式法 。积相同公因式1、计算下列各式:
x(x+1)= ;
(x+1)(x-1)= .复习与回顾:整式的乘法x2 + xx2-12、请把下列多项式写成整式乘积的形式.把一个多项式化成几个整式积的形式,这种变形叫做把这个多项式因式分解(或分解因式).想一想:因式分解与整式乘法有何关系? x2 + x
一个多项式因式分解与整式乘法是互逆过程.积的形式练习一 理解概念 判断下列各式哪些是整式乘法?哪些是因式分解?或者两者都不是?
(1) x2-(2y)2=(x+2y)(x-2y);
(2) 2x(x-3y)=2x2-6xy
(3)2πR+ 2πr= 2π(R+r)
(4) x2+4x+4=x(x+2)+4;
因式分解整式乘法因式分解不是因式分解也不是整式乘法经验提升:是否是因式分解看结果--乘积形式积的形式观察下列各式的结构有什么特点:(2) ma+mb(3) cx-cy+cz公共特点:各式中的各项都含有一个相同的因数或因式情景一:想一想探究新知多项式各项都含有的相同因式(或公共因式) 叫做这个多项式各项的公因式。
(1) 2πR+2πr(2) ma+mb(1) 2πR+2πr(3) cx-cy+cz合作探究用心观察,找到答案(2)多项式中的公因式是如何确定的?(合作交流探索)44a4a2b过关秘密武器:正确找出多项式各项公因式的关键是:公因式的系数是各项整数系数的 最大公约数。 定系数:取各项的相同的字母相同字母的指数取次数最低的,
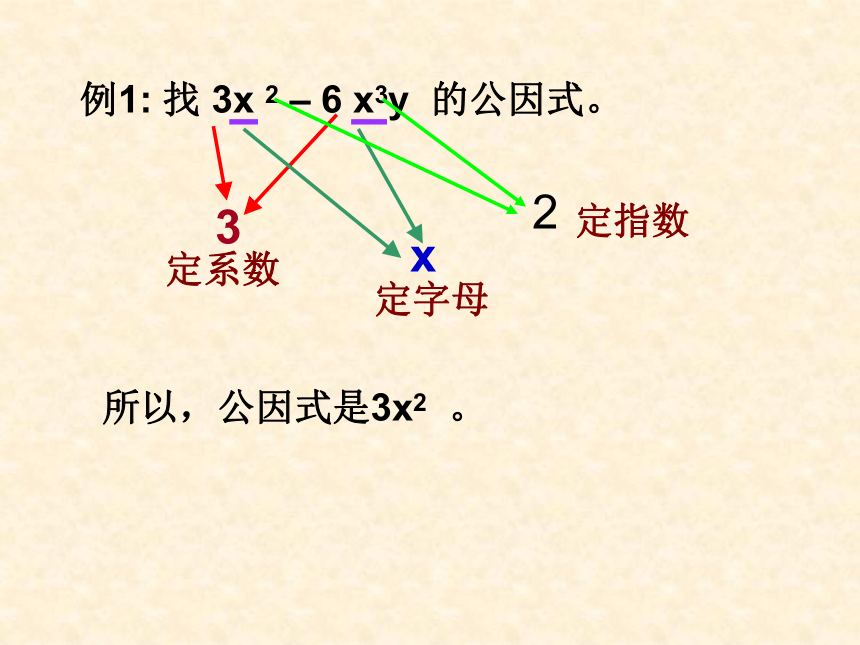
即相同字母最低次幂定字母:定指数:例1: 找 3x 2 – 6 x3y 的公因式。定系数3定字母x 所以,公因式是3x2 。定指数2快速出击1、分别写出下列多项式的公因式:(3)(1)(2)( a )( 3x2y )( 5a2b )探究新知 上例各式含有相同的数,将乘法分配律逆运用,把相同的因数写在括号外面,可使运算简便. 解: (1). 3.8x5+5.3x5+1.9x5=(3.8+5.3+1.9)x5=11x5=55(2). 20052-2005x2004=2005(2005-2004)=20052.请用简便的方法计算下列式子:(1). 3.8x5+5.3x5+1.9x5 (2).20052-2004x2005a m+b m +c m=( a + b + c ) m
= m( a + b + c )
a2 - a b = a ( a- b )上例中,多项式的各项含有公因式,将乘法分配律逆运用,把这个公因式提出来,使多项式化成两个因式积的形式.这种分解因式的方法叫做提公因式法.3.85.31.9abc=( a + b + c )a2=a×a知识储备解:原式=(1)7x2 - 21x7xx-3x←不能漏掉×知识储备(8a2b-12b2c)知识储备(3) 2a(b+c) - 3(b+c)分析:提公因式法步骤(分两步)
第一步:找出公因式;
第二步:提取公因式 ,即将多项式化为两个因式的乘积。
解:原式=(b+c)注意:公因式既可以是一个单项式的形式,
也可以是一个多项式的形式整体思想是数学中一种重要而且常用的思想方法。(2a-3)问题竞猜好礼等你拿小亮解的有误吗?试说明理由,并给出正解当多项式的某一项和公因式相同时,提公因式后剩余的项是1。错误注意:某项提出莫漏1。正确解:原式=3x.x-6y.x+1.x
=x(3x-6y+1) 若对多项式6a-18ax进行分解
因式,正确的选项( )
(A)6(a-3ax ) (B)3a(1+3x)
(C)3a(2-6x) (D)6a(1-3x)
D圣诞帽分解下列多项式解:原式=迷你音箱 若多项式(a+b)xy+(a+b)x要分解
因式,则要提的公因式是 .把 分解因式后得________ 应用拓展先分解因式,再求解:
已知a+b=5,ab=3,求a2b+ab2的值.解:卡西欧数码相机谈谈今天的收获2、确定公因式的方法:3、用提公因式法分解因式的步骤:1、什么叫公因式、提公因式法?4、用提公因式法分解因式应注意的问题:(1)小心漏项(如:1);(2)公因式可以是多项式形式。 1)定系数 2)定字母 3)定指数第一步,找出公因式;
第二步,提公因式( 把多项式化为两个因式的乘积)作业
课本 习题14.3:1题
同步练习再 见祝同学们:
天天快乐,
学业有成。
2. 了解整式乘法与因式分解的区别和联系是什么。
3. 理解什么是公因式?知道如何找公因式。
4. 初步掌握提公因式法。带着以上问题,自学课本仔细阅读课本,完成下列各题1、因式分解:把一个多项式化成几个整式的____的形式叫做把这个多项式因式分解。2、公因式:多项式的各项都含有一个________的因式,我们把这个因式叫做这个多项式的各项的公因式。 3、提公因式法:把多项式各项中的________提取出来,这种分解因式的方法叫做提公因式法 。积相同公因式1、计算下列各式:
x(x+1)= ;
(x+1)(x-1)= .复习与回顾:整式的乘法x2 + xx2-12、请把下列多项式写成整式乘积的形式.把一个多项式化成几个整式积的形式,这种变形叫做把这个多项式因式分解(或分解因式).想一想:因式分解与整式乘法有何关系? x2 + x
一个多项式因式分解与整式乘法是互逆过程.积的形式练习一 理解概念 判断下列各式哪些是整式乘法?哪些是因式分解?或者两者都不是?
(1) x2-(2y)2=(x+2y)(x-2y);
(2) 2x(x-3y)=2x2-6xy
(3)2πR+ 2πr= 2π(R+r)
(4) x2+4x+4=x(x+2)+4;
因式分解整式乘法因式分解不是因式分解也不是整式乘法经验提升:是否是因式分解看结果--乘积形式积的形式观察下列各式的结构有什么特点:(2) ma+mb(3) cx-cy+cz公共特点:各式中的各项都含有一个相同的因数或因式情景一:想一想探究新知多项式各项都含有的相同因式(或公共因式) 叫做这个多项式各项的公因式。
(1) 2πR+2πr(2) ma+mb(1) 2πR+2πr(3) cx-cy+cz合作探究用心观察,找到答案(2)多项式中的公因式是如何确定的?(合作交流探索)44a4a2b过关秘密武器:正确找出多项式各项公因式的关键是:公因式的系数是各项整数系数的 最大公约数。 定系数:取各项的相同的字母相同字母的指数取次数最低的,
即相同字母最低次幂定字母:定指数:例1: 找 3x 2 – 6 x3y 的公因式。定系数3定字母x 所以,公因式是3x2 。定指数2快速出击1、分别写出下列多项式的公因式:(3)(1)(2)( a )( 3x2y )( 5a2b )探究新知 上例各式含有相同的数,将乘法分配律逆运用,把相同的因数写在括号外面,可使运算简便. 解: (1). 3.8x5+5.3x5+1.9x5=(3.8+5.3+1.9)x5=11x5=55(2). 20052-2005x2004=2005(2005-2004)=20052.请用简便的方法计算下列式子:(1). 3.8x5+5.3x5+1.9x5 (2).20052-2004x2005a m+b m +c m=( a + b + c ) m
= m( a + b + c )
a2 - a b = a ( a- b )上例中,多项式的各项含有公因式,将乘法分配律逆运用,把这个公因式提出来,使多项式化成两个因式积的形式.这种分解因式的方法叫做提公因式法.3.85.31.9abc=( a + b + c )a2=a×a知识储备解:原式=(1)7x2 - 21x7xx-3x←不能漏掉×知识储备(8a2b-12b2c)知识储备(3) 2a(b+c) - 3(b+c)分析:提公因式法步骤(分两步)
第一步:找出公因式;
第二步:提取公因式 ,即将多项式化为两个因式的乘积。
解:原式=(b+c)注意:公因式既可以是一个单项式的形式,
也可以是一个多项式的形式整体思想是数学中一种重要而且常用的思想方法。(2a-3)问题竞猜好礼等你拿小亮解的有误吗?试说明理由,并给出正解当多项式的某一项和公因式相同时,提公因式后剩余的项是1。错误注意:某项提出莫漏1。正确解:原式=3x.x-6y.x+1.x
=x(3x-6y+1) 若对多项式6a-18ax进行分解
因式,正确的选项( )
(A)6(a-3ax ) (B)3a(1+3x)
(C)3a(2-6x) (D)6a(1-3x)
D圣诞帽分解下列多项式解:原式=迷你音箱 若多项式(a+b)xy+(a+b)x要分解
因式,则要提的公因式是 .把 分解因式后得________ 应用拓展先分解因式,再求解:
已知a+b=5,ab=3,求a2b+ab2的值.解:卡西欧数码相机谈谈今天的收获2、确定公因式的方法:3、用提公因式法分解因式的步骤:1、什么叫公因式、提公因式法?4、用提公因式法分解因式应注意的问题:(1)小心漏项(如:1);(2)公因式可以是多项式形式。 1)定系数 2)定字母 3)定指数第一步,找出公因式;
第二步,提公因式( 把多项式化为两个因式的乘积)作业
课本 习题14.3:1题
同步练习再 见祝同学们:
天天快乐,
学业有成。
