人教版七年级下册9.2一元一次不等式 教学设计
文档属性
| 名称 | 人教版七年级下册9.2一元一次不等式 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 36.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 00:00:00 | ||
图片预览


文档简介
一元一次不等式 教学设计
基本信息
学段 初中 学科 数学
使用教材版本 人教版七年级下册
课题 9.2一元一次不等式(第1课时)
课型 新授课 章/单元复习课□ 专题复习课□ 习题/试卷讲评课□ 学科实践活动课□ 其他□
1.单元教学内容分析
本课时是七年级下册第九章不等式与不等式组中的一节内容,本章第一节介绍了不等式的概念以及解法,类比等式的性质得到不等式的性质,第二节类比一元一次方程得到一元一次不等式的概念及解法,以及如何根据实际问题列不等式,进而解决实际问题,第三节介绍一元一次不等式组的概念以及解法,如数轴法、口诀法。本章主要培养学生的抽象能力,以及数形结合的思想,将实际问题抽象成数学问题,通过所学知识帮助解决实际问题。
2.本课时教学内容分析
本课时位于第二节第一课时,主要介绍一元一次不等式的概念及解法,通过类比一元一次方程的概念及解法,学生更容易掌握本课时内容,加强了对学生类比思维能力的培养,在解出不等式后,学生可将借助之前学习的数轴,将不等式的解集在数轴上表示出来,更好的体会数形结合的思想。
3.学习者分析
学生在学习本课时之前已经学习了不等式的概念和解法,并且学习过一元一次方程的概念和解法,以及数轴的相关知识。学生在学习本课时时可能碰到的困难是求解不等式时不等号方向的改变,以及用数轴表示解集时解集的画法。
4.教学目标
1.了解一元一次不等式的概念,掌握一元一次不等式的解法. 2.会用不等式的性质,类比一元一次方程的解法得到一元一次不等式的解法,体会知识的迁移. 3.通过讨论、交流的过程体验充满着探索性和创造性.
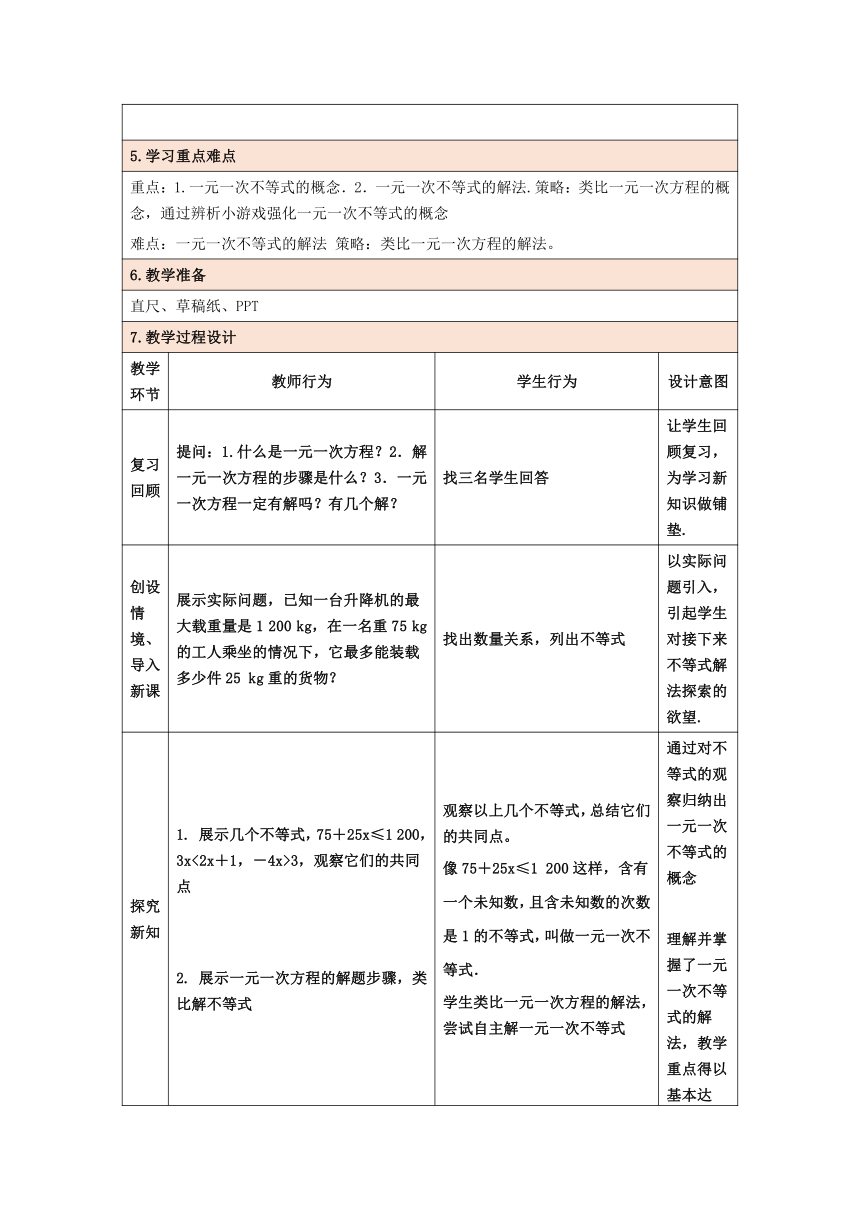
5.学习重点难点
重点:1.一元一次不等式的概念.2.一元一次不等式的解法.策略:类比一元一次方程的概念,通过辨析小游戏强化一元一次不等式的概念 难点:一元一次不等式的解法 策略:类比一元一次方程的解法。
6.教学准备
直尺、草稿纸、PPT
7.教学过程设计
教学环节 教师行为 学生行为 设计意图
复习回顾 提问:1.什么是一元一次方程?2.解一元一次方程的步骤是什么?3.一元一次方程一定有解吗?有几个解? 找三名学生回答 让学生回顾复习,为学习新知识做铺垫.
创设情境、导入新课 展示实际问题,已知一台升降机的最大载重量是1 200 kg,在一名重75 kg的工人乘坐的情况下,它最多能装载多少件25 kg重的货物? 找出数量关系,列出不等式 以实际问题引入,引起学生对接下来不等式解法探索的欲望.
探究新知 展示几个不等式,75+25x≤1 200,3x<2x+1,-4x>3,观察它们的共同点 展示一元一次方程的解题步骤,类比解不等式 观察以上几个不等式,总结它们的共同点。 像75+25x≤1 200这样,含有一个未知数,且含未知数的次数是1的不等式,叫做一元一次不等式. 学生类比一元一次方程的解法,尝试自主解一元一次不等式 通过对不等式的观察归纳出一元一次不等式的概念 理解并掌握了一元一次不等式的解法,教学重点得以基本达成,教学难点也取得相应突破.
课堂练习 例 (教材第122页例1)解下列不等式,并在数轴上表示解集: (1)2(1+x)<3;(2)≥. 【变式训练】 解下列不等式,并在数轴上表示解集: (1)3(x-1)<4(x-)-3;(2)-≤1. 解:(1)去括号,得2+2x<3. 移项,得2x<3-2. 合并同类项,得2x<1. 系数化为1,得x<. 这个不等式的解集在数轴上的表示如图所示: (2)去分母,得3(2+x)≥2(2x-1). 去括号,得6+3x≥4x-2. 移项,得3x-4x≥-2-6. 合并同类项,得-x≥-8. 系数化为1,得x≤8. 这个不等式的解集在数轴上表示如图: 解:(1)去括号,得3x-3<4x-2-3. 移项,得3x-4x<3-2-3. 合并同类项,得-x<-2. 系数化为1,得x>2. 其解集在数轴上表示为: (2)去分母,得2(2x-1)-(9x+2)≤6. 去括号,得4x-2-9x-2≤6. 移项,得4x-9x≤6+2+2. 合并同类项,得-5x≤10. 系数化为1,得x≥-2. 其解集在数轴上表示为: 通过例题和变式训练,及时巩固所学知识,反馈学生的学习情况,培养学生综合运用不等式的性质解决问题的能力,进一步提升学习效果.
课堂检测 【课堂检测】 1.不等式5x-1>2x+5的解集在数轴上表示正确的是(A) 2.在下列解不等式>的过程中,错误的一步是(D) A.去分母,得5(2+x)>3(2x-1) B.去括号,得10+5x>6x-3 C.移项,得5x-6x>-3-10 D.合并同类项、系数化为1,得x>13 3.与不等式-x≤-1的解集相同的不等式是(D) A.-2x≤-1 B.-2x≤x-10 C.-4x≥x-10 D.-4x≤x-10 4.若关于x的方程4x-2m+1=5x-8的解是负数,则m的取值范围为(A) A.m> B.m<0 C.m< D.m>0 5.3(x+1)≥5x-3的正整数解是1,2,3. 6.解不等式,并把解集在数轴上表示出来: (1)2(x-1)+5<3x; 解:去括号,得2x-2+5<3x. 移项,得2x-3x<2-5. 合并同类项,得-x<-3. 系数化为1,得x>3. 其解集在数轴上表示为: 课堂检测及时获知学生对所学知识的掌握情况,并最大限度地调动全体学生学习数学的积极性,使每个学生都能有所收益、有所提高。
课堂小结 课堂小结: 学生试述:解一元一次不等式的一般步骤和注意事项. 注重课堂小结,激发学生参与课堂总结的主动性,为每一个学生的发展与表现创造机会
8.板书设计
9.2一元一次不等式(第1课时) 复习回顾 情景引入 探索新知 一元一次不等式的概念: 含有一个未知数,且含未知数的次数是1的不等式,叫做一元一次不等式. 2.一元一次不等式的解题步骤 课堂练习 课堂小结
9.作业与拓展学习设计
(1)教材第124页练习. (2)教材第126页习题9.2第1,2,3题.
10.教学反思与改进
在整个教学过程中,学生参与度高,对知识的掌握比较顺利,并且能够灵活应用,学习目标顺利达成,教学重点难点都有顺利突破。 改进点:可在以后的教学过程中增加小组讨论,培养学生合作探究的意识。
基本信息
学段 初中 学科 数学
使用教材版本 人教版七年级下册
课题 9.2一元一次不等式(第1课时)
课型 新授课 章/单元复习课□ 专题复习课□ 习题/试卷讲评课□ 学科实践活动课□ 其他□
1.单元教学内容分析
本课时是七年级下册第九章不等式与不等式组中的一节内容,本章第一节介绍了不等式的概念以及解法,类比等式的性质得到不等式的性质,第二节类比一元一次方程得到一元一次不等式的概念及解法,以及如何根据实际问题列不等式,进而解决实际问题,第三节介绍一元一次不等式组的概念以及解法,如数轴法、口诀法。本章主要培养学生的抽象能力,以及数形结合的思想,将实际问题抽象成数学问题,通过所学知识帮助解决实际问题。
2.本课时教学内容分析
本课时位于第二节第一课时,主要介绍一元一次不等式的概念及解法,通过类比一元一次方程的概念及解法,学生更容易掌握本课时内容,加强了对学生类比思维能力的培养,在解出不等式后,学生可将借助之前学习的数轴,将不等式的解集在数轴上表示出来,更好的体会数形结合的思想。
3.学习者分析
学生在学习本课时之前已经学习了不等式的概念和解法,并且学习过一元一次方程的概念和解法,以及数轴的相关知识。学生在学习本课时时可能碰到的困难是求解不等式时不等号方向的改变,以及用数轴表示解集时解集的画法。
4.教学目标
1.了解一元一次不等式的概念,掌握一元一次不等式的解法. 2.会用不等式的性质,类比一元一次方程的解法得到一元一次不等式的解法,体会知识的迁移. 3.通过讨论、交流的过程体验充满着探索性和创造性.
5.学习重点难点
重点:1.一元一次不等式的概念.2.一元一次不等式的解法.策略:类比一元一次方程的概念,通过辨析小游戏强化一元一次不等式的概念 难点:一元一次不等式的解法 策略:类比一元一次方程的解法。
6.教学准备
直尺、草稿纸、PPT
7.教学过程设计
教学环节 教师行为 学生行为 设计意图
复习回顾 提问:1.什么是一元一次方程?2.解一元一次方程的步骤是什么?3.一元一次方程一定有解吗?有几个解? 找三名学生回答 让学生回顾复习,为学习新知识做铺垫.
创设情境、导入新课 展示实际问题,已知一台升降机的最大载重量是1 200 kg,在一名重75 kg的工人乘坐的情况下,它最多能装载多少件25 kg重的货物? 找出数量关系,列出不等式 以实际问题引入,引起学生对接下来不等式解法探索的欲望.
探究新知 展示几个不等式,75+25x≤1 200,3x<2x+1,-4x>3,观察它们的共同点 展示一元一次方程的解题步骤,类比解不等式 观察以上几个不等式,总结它们的共同点。 像75+25x≤1 200这样,含有一个未知数,且含未知数的次数是1的不等式,叫做一元一次不等式. 学生类比一元一次方程的解法,尝试自主解一元一次不等式 通过对不等式的观察归纳出一元一次不等式的概念 理解并掌握了一元一次不等式的解法,教学重点得以基本达成,教学难点也取得相应突破.
课堂练习 例 (教材第122页例1)解下列不等式,并在数轴上表示解集: (1)2(1+x)<3;(2)≥. 【变式训练】 解下列不等式,并在数轴上表示解集: (1)3(x-1)<4(x-)-3;(2)-≤1. 解:(1)去括号,得2+2x<3. 移项,得2x<3-2. 合并同类项,得2x<1. 系数化为1,得x<. 这个不等式的解集在数轴上的表示如图所示: (2)去分母,得3(2+x)≥2(2x-1). 去括号,得6+3x≥4x-2. 移项,得3x-4x≥-2-6. 合并同类项,得-x≥-8. 系数化为1,得x≤8. 这个不等式的解集在数轴上表示如图: 解:(1)去括号,得3x-3<4x-2-3. 移项,得3x-4x<3-2-3. 合并同类项,得-x<-2. 系数化为1,得x>2. 其解集在数轴上表示为: (2)去分母,得2(2x-1)-(9x+2)≤6. 去括号,得4x-2-9x-2≤6. 移项,得4x-9x≤6+2+2. 合并同类项,得-5x≤10. 系数化为1,得x≥-2. 其解集在数轴上表示为: 通过例题和变式训练,及时巩固所学知识,反馈学生的学习情况,培养学生综合运用不等式的性质解决问题的能力,进一步提升学习效果.
课堂检测 【课堂检测】 1.不等式5x-1>2x+5的解集在数轴上表示正确的是(A) 2.在下列解不等式>的过程中,错误的一步是(D) A.去分母,得5(2+x)>3(2x-1) B.去括号,得10+5x>6x-3 C.移项,得5x-6x>-3-10 D.合并同类项、系数化为1,得x>13 3.与不等式-x≤-1的解集相同的不等式是(D) A.-2x≤-1 B.-2x≤x-10 C.-4x≥x-10 D.-4x≤x-10 4.若关于x的方程4x-2m+1=5x-8的解是负数,则m的取值范围为(A) A.m> B.m<0 C.m< D.m>0 5.3(x+1)≥5x-3的正整数解是1,2,3. 6.解不等式,并把解集在数轴上表示出来: (1)2(x-1)+5<3x; 解:去括号,得2x-2+5<3x. 移项,得2x-3x<2-5. 合并同类项,得-x<-3. 系数化为1,得x>3. 其解集在数轴上表示为: 课堂检测及时获知学生对所学知识的掌握情况,并最大限度地调动全体学生学习数学的积极性,使每个学生都能有所收益、有所提高。
课堂小结 课堂小结: 学生试述:解一元一次不等式的一般步骤和注意事项. 注重课堂小结,激发学生参与课堂总结的主动性,为每一个学生的发展与表现创造机会
8.板书设计
9.2一元一次不等式(第1课时) 复习回顾 情景引入 探索新知 一元一次不等式的概念: 含有一个未知数,且含未知数的次数是1的不等式,叫做一元一次不等式. 2.一元一次不等式的解题步骤 课堂练习 课堂小结
9.作业与拓展学习设计
(1)教材第124页练习. (2)教材第126页习题9.2第1,2,3题.
10.教学反思与改进
在整个教学过程中,学生参与度高,对知识的掌握比较顺利,并且能够灵活应用,学习目标顺利达成,教学重点难点都有顺利突破。 改进点:可在以后的教学过程中增加小组讨论,培养学生合作探究的意识。
