3.1.2 函数的表示法课件——高中数学人教A版(2019)必修第一册
文档属性
| 名称 | 3.1.2 函数的表示法课件——高中数学人教A版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 16:31:12 | ||
图片预览








文档简介
(共33张PPT)
人教高中A版必修一数学课件
第2课时 函数的表示法
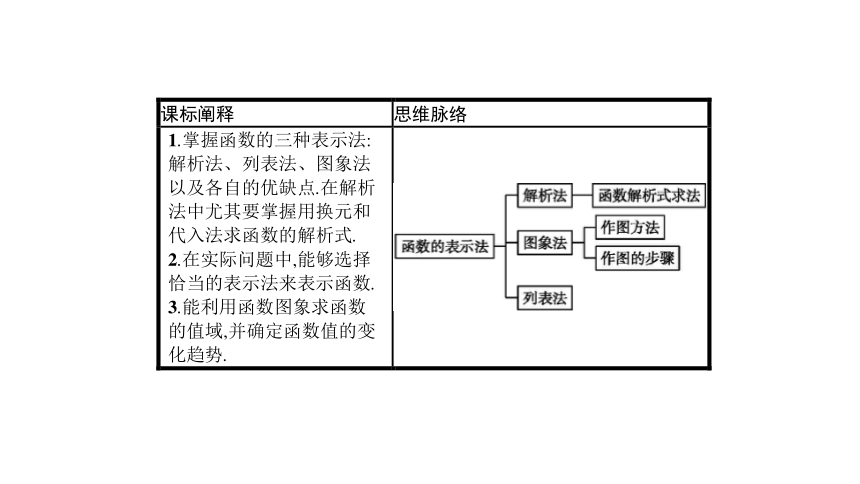
学习目标
01
一
二
一、函数的表示法
1.(1)初中学过的3种常用的函数的表示方法是如何定义的
提示:①解析法:用数学表达式表示两个变量之间的对应关系;②图象法:用图象表示两个变量之间的对应关系;③列表法:列出表格来表示两个变量之间的对应关系.
(2)教材P60~P61问题1~问题4,分别是用什么方法表示函数的
提示:问题1、2是用解析法,问题3是用图象法,问题4是用列表法.
一
二
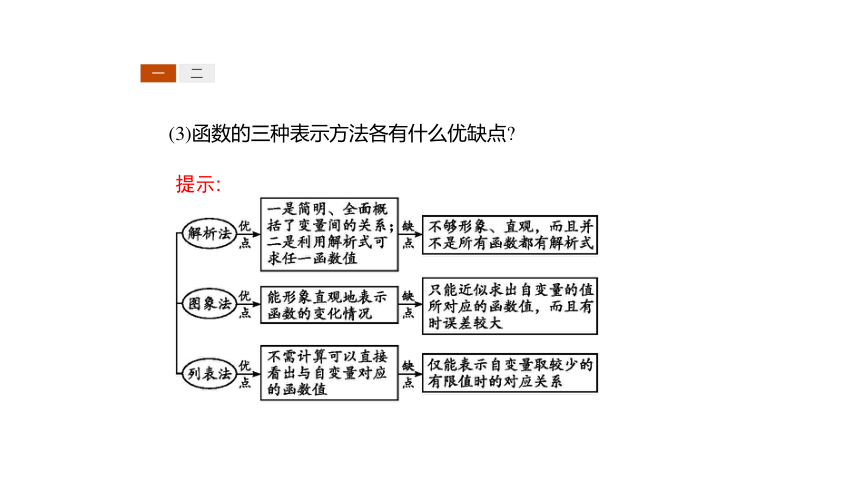
(3)函数的三种表示方法各有什么优缺点
一
二
(4)做一做
某同学计划买x(x∈{1,2,3,4,5})支2B铅笔,每支铅笔的价格为0.5元,共需y元,于是y与x之间建立起了一个函数关系.
①函数的定义域是什么
提示:{1,2,3,4,5}
②y与x有何关系
提示:y=0.5x
③试用表格表示y与x之间的关系.
提示:表格如下:
一
二
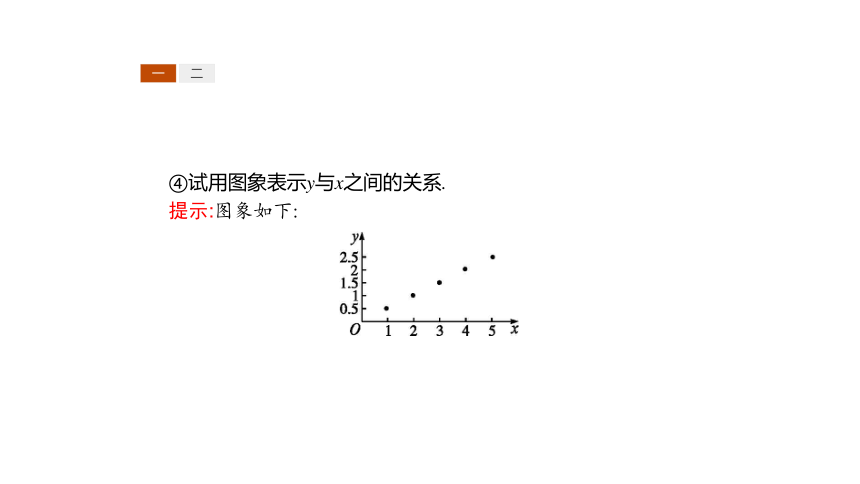
④试用图象表示y与x之间的关系.
提示:图象如下:
一
二
二、函数的图象
1.(1)初中我们已研究过直线、反比例函数及二次函数的图象,请作出y=2x-1,y= ,y=x2的图象.观察这些图象有什么共同特点
提示:共同的特点是由满足一定条件的点构成的,具体地说就是将函数y=f(x)中的自变量x作为横坐标、对应因变量y作为纵坐标描成点,所有的点即构成该函数的图象.
(2)如何作出函数y=f(x)的图象
提示:将自变量的一个值x0作为横坐标就得到坐标平面上的一个点(x0,f(x0)),自变量取遍函数定义域A的每个值时,就得到一系列这样的点,所有这些点组成的集合(点集)为{(x,y)|y=f(x),x∈A},这些点组成的曲线就是函数y=f(x)的图象.
一
二
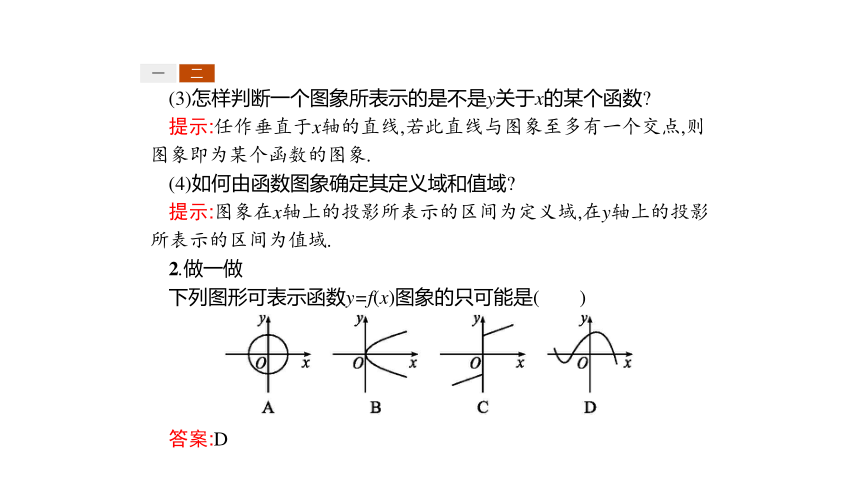
(3)怎样判断一个图象所表示的是不是y关于x的某个函数
提示:任作垂直于x轴的直线,若此直线与图象至多有一个交点,则图象即为某个函数的图象.
(4)如何由函数图象确定其定义域和值域
提示:图象在x轴上的投影所表示的区间为定义域,在y轴上的投影所表示的区间为值域.
2.做一做
下列图形可表示函数y=f(x)图象的只可能是( )
答案:D
新知探究
02
探究一
探究二
探究三
思维辨析
随堂演练
列表法表示函数
例1 (一题多空题)已知函数f(x),g(x)分别由下表给出:
则f(g(1))= ;当g(f(x))=2时,x= .
分析:这是用列表法表示的函数求值问题,在解答时,找准变量对应的值即可.
解析:由g(x)的对应表,知g(1)=3,∴f(g(1))=f(3).
由f(x)的对应表,知f(3)=1,∴f(g(1))=f(3)=1.
由g(x)的对应表,知当x=2时,g(2)=2.
又g(f(x))=2,∴f(x)=2.又由f(x)的对应表,知当x=1时,f(1)=2.∴x=1.
答案:1 1
探究一
探究二
探究三
思维辨析
随堂演练
反思感悟 列表法是表示函数的重要方法,这如同我们在画函数图象时所列的表,它的明显优点是变量对应的函数值在表中可直接找到,不需要计算.
探究一
探究二
探究三
思维辨析
随堂演练
延伸探究在本例已知条件下,g(f(1))= ;当f(g(x))=2时,x= .
解析:∵f(1)=2,∴g(f(1))=g(2)=2.
∵f(g(x))=2,∴g(x)=1,∴x=3.
答案:2 3
探究一
探究二
探究三
思维辨析
随堂演练
求函数的解析式
例2 (1)已知f(x+1)=x2-3x+2,求f(x);
(2)已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x,求f(x)的解析式;
(3)已知函数f(x)对于任意的x都有f(x)+2f(-x)=3x-2,求f(x).
分析:(1)(方法一)令x+1=t,将x=t-1代入f(x+1)=x2-3x+2可得f(t),即可得f(x);(方法二)由于f(x+1)中x+1的地位与f(x)中x的地位相同,因此还可以将f(x+1)变形为f(x+1)=(x+1)2-5(x+1)+6.(2)设出f(x)=ax2+bx+c(a≠0),再根据条件列出方程组求出a,b,c的值.(3)将f(x)+2f(-x)=3x-2中的x用-x代替,解关于f(x)与f(-x)的方程组即可.
探究一
探究二
探究三
思维辨析
随堂演练
解:(1)(方法一)令x+1=t,则x=t-1.
将x=t-1代入f(x+1)=x2-3x+2,
得f(t)=(t-1)2-3(t-1)+2=t2-5t+6,
∴f(x)=x2-5x+6.
(方法二)∵f(x+1)=x2-3x+2=x2+2x+1-5x-5+6=(x+1)2-5(x+1)+6,
∴f(x)=x2-5x+6.
(2)设所求的二次函数为f(x)=ax2+bx+c(a≠0).
∵f(0)=1,∴c=1,则f(x)=ax2+bx+1.
∵f(x+1)-f(x)=2x对任意的x∈R都成立,
∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x,
探究一
探究二
探究三
思维辨析
随堂演练
(3)∵对于任意的x都有f(x)+2f(-x)=3x-2,
∴将x替换为-x,得f(-x)+2f(x)=-3x-2,联立方程组消去f(-x),可得f(x)=-3x- .
探究一
探究二
探究三
思维辨析
随堂演练
反思感悟 求函数解析式的四种常用方法
1.直接法(代入法):已知f(x)的解析式,求f(g(x))的解析式,直接将g(x)代入即可.
2.待定系数法:若已知函数的类型,可用待定系数法求解,即由函数类型设出函数解析式,再根据条件列方程(或方程组),通过解方程(组)求出待定系数,进而求出函数解析式.
3.换元法(有时可用“配凑法”):已知函数f(g(x))的解析式求f(x)的解析式可用换元法(或“配凑法”),即令g(x)=t,反解出x,然后代入f(g(x))中求出f(t),从而求出f(x).
4.解方程组法或消元法:在已知式子中,含有关于两个不同变量的函数,而这两个变量有着某种关系,这时就要依据两个变量的关系,建立一个新的关于两个变量的式子,由两个式子建立方程组,通过解方程组消去一个变量,得到目标变量的解析式,这种方法叫做解方程组法或消元法.
探究一
探究二
探究三
思维辨析
随堂演练
变式训练1(1)已知f(x)是一次函数,且f(f(x))=2x-1,求f(x)的解析式;
解:(1)∵f(x)为一次函数,
∴可设f(x)=ax+b(a≠0).
∵f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b=2x-1.
探究一
探究二
探究三
思维辨析
随堂演练
故所求函数的解析式为f(x)=x2-1,其中x≥1.
探究一
探究二
探究三
思维辨析
随堂演练
函数的图象及应用
例3 作出下列函数的图象,并求其值域:
(1)y=1-x(x∈Z);(2)y=2x2-4x-3(0≤x<3).
分析:看函数的类型→看函数的定义域→描点、连线、成图.
解:(1)因为x∈Z,所以函数图象为一条直线上的孤立点(如图①),由图象知,y∈Z.
(2)因为x∈[0,3),所以函数图象是抛物线的一段(如图②),由图象知,y∈[-5,3).
探究一
探究二
探究三
思维辨析
随堂演练
反思感悟 1.作函数图象最基本的方法是描点法:主要有三个步骤——列表、描点、连线.作图象时一般先确定函数的定义域,再在定义域内化简函数解析式,最后列表画出图象.
2.函数的图象可能是平滑的曲线,也可能是一群孤立的点,画图时要注意特殊点.如图象与坐标轴的交点、区间端点、二次函数的顶点等,还要分清这些特殊点是实心点还是空心点.
如本题(1)中图象是由一些散点构成的,这里不能将其用平滑曲线连起来;(2)中描出两个端点及顶点,依据二次函数的图象特征作出函数图象,注意3不在定义域内,从而点(3,3)处用空心点.
探究一
探究二
探究三
思维辨析
随堂演练
变式训练2作出下列函数的图象,并写出其值域.
(1)y=2x+1,x∈[0,2];
解:(1)当x=0时,y=1;当x=1时,y=3;当x=2时,y=5.
函数图象过点(0,1),(1,3),(2,5).
图象如图所示.
由图可知,函数的值域为[0,5].
由图可知,函数的值域为(0,1].
巩固练习
03
探究一
探究二
探究三
思维辨析
随堂演练
因忽略变量的实际意义而致错
典例如图,在矩形ABCD中,BA=3,CB=4,点P在AD上移动,CQ⊥BP,Q为垂足.设BP=x,CQ=y,试求y关于x的函数表达式,并画出函数的图象.
错解由题意,得△CQB∽△BAP,
探究一
探究二
探究三
思维辨析
随堂演练
以上解题过程中都有哪些错误 出错的原因是什么 你如何改正 如何防范
提示:以上解题过程中没有考虑x的实际意义,从而扩大了x的取值范围而导致出错.
探究一
探究二
探究三
思维辨析
随堂演练
正解:由题意,得△CQB∽△BAP,
防范措施从实际问题中得到的函数,求其定义域时,不仅要使函数有意义,而且还要使实际问题有意义.
探究一
探究二
探究三
思维辨析
随堂演练
变式训练已知一个面积为100 cm2的等腰梯形,上底长为x cm,下底长为上底长的3倍,则把它的高y表示成x的函数为( )
答案:C
拓展延伸
04
探究一
探究二
探究三
思维辨析
随堂演练
1.已知一次函数的图象过点(1,0)和(0,1),则该一次函数的解析式为( )
A.f(x)=-x B.f(x)=x-1
C.f(x)=x+1 D.f(x)=-x+1
所以a=-1,b=1,即f(x)=-x+1.
答案:D
探究一
探究二
探究三
思维辨析
随堂演练
2.某天早上,小明骑车上学,出发时感到时间较紧,然后加速前进,后来发现时间还比较充裕,于是放慢了速度,与以上事件吻合得最好的图象是( )
解析:因为选项A,D第一段都是匀速前进,不合题意,故排除选项A,D,首先加速前进,然后放慢速度,说明图象上升的速度先快后慢,故选C.
答案:C
探究一
探究二
探究三
思维辨析
随堂演练
3.已知函数f(x),g(x)对应值如下表:
则g(f(g(-1)))的值为( )
A.1 B.0
C.-1 D.无法确定
解析:g(-1)=1,
则f(g(-1))=f(1)=0,
则g(f(g(-1)))=g(0)=-1.
答案:C
探究一
探究二
探究三
思维辨析
随堂演练
4.若一个长方体的高为80 cm,长比宽多10 cm,则这个长方体的体积y(单位:cm3)与长方体的宽x(单位:cm)之间的函数表达式是 .
解析:由题意可知,长方体的长为(x+10)cm,从而长方体的体积y=80x(x+10),x>0.
答案:y=80x(x+10),x∈(0,+∞)
探究一
探究二
探究三
思维辨析
随堂演练
5.已知函数f(x)=x2-2x(-1≤x≤2).
(1)画出f(x)的图象;
(2)根据图象写出f(x)的值域.
解:(1)f(x)的图象如图所示.
(2)观察f(x)的图象可知,f(x)图象上所有点的纵坐标的取值范围是[-1,3],故f(x)的值域是[-1,3].
人教高中A版必修一数学课件
第2课时 函数的表示法
学习目标
01
一
二
一、函数的表示法
1.(1)初中学过的3种常用的函数的表示方法是如何定义的
提示:①解析法:用数学表达式表示两个变量之间的对应关系;②图象法:用图象表示两个变量之间的对应关系;③列表法:列出表格来表示两个变量之间的对应关系.
(2)教材P60~P61问题1~问题4,分别是用什么方法表示函数的
提示:问题1、2是用解析法,问题3是用图象法,问题4是用列表法.
一
二
(3)函数的三种表示方法各有什么优缺点
一
二
(4)做一做
某同学计划买x(x∈{1,2,3,4,5})支2B铅笔,每支铅笔的价格为0.5元,共需y元,于是y与x之间建立起了一个函数关系.
①函数的定义域是什么
提示:{1,2,3,4,5}
②y与x有何关系
提示:y=0.5x
③试用表格表示y与x之间的关系.
提示:表格如下:
一
二
④试用图象表示y与x之间的关系.
提示:图象如下:
一
二
二、函数的图象
1.(1)初中我们已研究过直线、反比例函数及二次函数的图象,请作出y=2x-1,y= ,y=x2的图象.观察这些图象有什么共同特点
提示:共同的特点是由满足一定条件的点构成的,具体地说就是将函数y=f(x)中的自变量x作为横坐标、对应因变量y作为纵坐标描成点,所有的点即构成该函数的图象.
(2)如何作出函数y=f(x)的图象
提示:将自变量的一个值x0作为横坐标就得到坐标平面上的一个点(x0,f(x0)),自变量取遍函数定义域A的每个值时,就得到一系列这样的点,所有这些点组成的集合(点集)为{(x,y)|y=f(x),x∈A},这些点组成的曲线就是函数y=f(x)的图象.
一
二
(3)怎样判断一个图象所表示的是不是y关于x的某个函数
提示:任作垂直于x轴的直线,若此直线与图象至多有一个交点,则图象即为某个函数的图象.
(4)如何由函数图象确定其定义域和值域
提示:图象在x轴上的投影所表示的区间为定义域,在y轴上的投影所表示的区间为值域.
2.做一做
下列图形可表示函数y=f(x)图象的只可能是( )
答案:D
新知探究
02
探究一
探究二
探究三
思维辨析
随堂演练
列表法表示函数
例1 (一题多空题)已知函数f(x),g(x)分别由下表给出:
则f(g(1))= ;当g(f(x))=2时,x= .
分析:这是用列表法表示的函数求值问题,在解答时,找准变量对应的值即可.
解析:由g(x)的对应表,知g(1)=3,∴f(g(1))=f(3).
由f(x)的对应表,知f(3)=1,∴f(g(1))=f(3)=1.
由g(x)的对应表,知当x=2时,g(2)=2.
又g(f(x))=2,∴f(x)=2.又由f(x)的对应表,知当x=1时,f(1)=2.∴x=1.
答案:1 1
探究一
探究二
探究三
思维辨析
随堂演练
反思感悟 列表法是表示函数的重要方法,这如同我们在画函数图象时所列的表,它的明显优点是变量对应的函数值在表中可直接找到,不需要计算.
探究一
探究二
探究三
思维辨析
随堂演练
延伸探究在本例已知条件下,g(f(1))= ;当f(g(x))=2时,x= .
解析:∵f(1)=2,∴g(f(1))=g(2)=2.
∵f(g(x))=2,∴g(x)=1,∴x=3.
答案:2 3
探究一
探究二
探究三
思维辨析
随堂演练
求函数的解析式
例2 (1)已知f(x+1)=x2-3x+2,求f(x);
(2)已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x,求f(x)的解析式;
(3)已知函数f(x)对于任意的x都有f(x)+2f(-x)=3x-2,求f(x).
分析:(1)(方法一)令x+1=t,将x=t-1代入f(x+1)=x2-3x+2可得f(t),即可得f(x);(方法二)由于f(x+1)中x+1的地位与f(x)中x的地位相同,因此还可以将f(x+1)变形为f(x+1)=(x+1)2-5(x+1)+6.(2)设出f(x)=ax2+bx+c(a≠0),再根据条件列出方程组求出a,b,c的值.(3)将f(x)+2f(-x)=3x-2中的x用-x代替,解关于f(x)与f(-x)的方程组即可.
探究一
探究二
探究三
思维辨析
随堂演练
解:(1)(方法一)令x+1=t,则x=t-1.
将x=t-1代入f(x+1)=x2-3x+2,
得f(t)=(t-1)2-3(t-1)+2=t2-5t+6,
∴f(x)=x2-5x+6.
(方法二)∵f(x+1)=x2-3x+2=x2+2x+1-5x-5+6=(x+1)2-5(x+1)+6,
∴f(x)=x2-5x+6.
(2)设所求的二次函数为f(x)=ax2+bx+c(a≠0).
∵f(0)=1,∴c=1,则f(x)=ax2+bx+1.
∵f(x+1)-f(x)=2x对任意的x∈R都成立,
∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x,
探究一
探究二
探究三
思维辨析
随堂演练
(3)∵对于任意的x都有f(x)+2f(-x)=3x-2,
∴将x替换为-x,得f(-x)+2f(x)=-3x-2,联立方程组消去f(-x),可得f(x)=-3x- .
探究一
探究二
探究三
思维辨析
随堂演练
反思感悟 求函数解析式的四种常用方法
1.直接法(代入法):已知f(x)的解析式,求f(g(x))的解析式,直接将g(x)代入即可.
2.待定系数法:若已知函数的类型,可用待定系数法求解,即由函数类型设出函数解析式,再根据条件列方程(或方程组),通过解方程(组)求出待定系数,进而求出函数解析式.
3.换元法(有时可用“配凑法”):已知函数f(g(x))的解析式求f(x)的解析式可用换元法(或“配凑法”),即令g(x)=t,反解出x,然后代入f(g(x))中求出f(t),从而求出f(x).
4.解方程组法或消元法:在已知式子中,含有关于两个不同变量的函数,而这两个变量有着某种关系,这时就要依据两个变量的关系,建立一个新的关于两个变量的式子,由两个式子建立方程组,通过解方程组消去一个变量,得到目标变量的解析式,这种方法叫做解方程组法或消元法.
探究一
探究二
探究三
思维辨析
随堂演练
变式训练1(1)已知f(x)是一次函数,且f(f(x))=2x-1,求f(x)的解析式;
解:(1)∵f(x)为一次函数,
∴可设f(x)=ax+b(a≠0).
∵f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b=2x-1.
探究一
探究二
探究三
思维辨析
随堂演练
故所求函数的解析式为f(x)=x2-1,其中x≥1.
探究一
探究二
探究三
思维辨析
随堂演练
函数的图象及应用
例3 作出下列函数的图象,并求其值域:
(1)y=1-x(x∈Z);(2)y=2x2-4x-3(0≤x<3).
分析:看函数的类型→看函数的定义域→描点、连线、成图.
解:(1)因为x∈Z,所以函数图象为一条直线上的孤立点(如图①),由图象知,y∈Z.
(2)因为x∈[0,3),所以函数图象是抛物线的一段(如图②),由图象知,y∈[-5,3).
探究一
探究二
探究三
思维辨析
随堂演练
反思感悟 1.作函数图象最基本的方法是描点法:主要有三个步骤——列表、描点、连线.作图象时一般先确定函数的定义域,再在定义域内化简函数解析式,最后列表画出图象.
2.函数的图象可能是平滑的曲线,也可能是一群孤立的点,画图时要注意特殊点.如图象与坐标轴的交点、区间端点、二次函数的顶点等,还要分清这些特殊点是实心点还是空心点.
如本题(1)中图象是由一些散点构成的,这里不能将其用平滑曲线连起来;(2)中描出两个端点及顶点,依据二次函数的图象特征作出函数图象,注意3不在定义域内,从而点(3,3)处用空心点.
探究一
探究二
探究三
思维辨析
随堂演练
变式训练2作出下列函数的图象,并写出其值域.
(1)y=2x+1,x∈[0,2];
解:(1)当x=0时,y=1;当x=1时,y=3;当x=2时,y=5.
函数图象过点(0,1),(1,3),(2,5).
图象如图所示.
由图可知,函数的值域为[0,5].
由图可知,函数的值域为(0,1].
巩固练习
03
探究一
探究二
探究三
思维辨析
随堂演练
因忽略变量的实际意义而致错
典例如图,在矩形ABCD中,BA=3,CB=4,点P在AD上移动,CQ⊥BP,Q为垂足.设BP=x,CQ=y,试求y关于x的函数表达式,并画出函数的图象.
错解由题意,得△CQB∽△BAP,
探究一
探究二
探究三
思维辨析
随堂演练
以上解题过程中都有哪些错误 出错的原因是什么 你如何改正 如何防范
提示:以上解题过程中没有考虑x的实际意义,从而扩大了x的取值范围而导致出错.
探究一
探究二
探究三
思维辨析
随堂演练
正解:由题意,得△CQB∽△BAP,
防范措施从实际问题中得到的函数,求其定义域时,不仅要使函数有意义,而且还要使实际问题有意义.
探究一
探究二
探究三
思维辨析
随堂演练
变式训练已知一个面积为100 cm2的等腰梯形,上底长为x cm,下底长为上底长的3倍,则把它的高y表示成x的函数为( )
答案:C
拓展延伸
04
探究一
探究二
探究三
思维辨析
随堂演练
1.已知一次函数的图象过点(1,0)和(0,1),则该一次函数的解析式为( )
A.f(x)=-x B.f(x)=x-1
C.f(x)=x+1 D.f(x)=-x+1
所以a=-1,b=1,即f(x)=-x+1.
答案:D
探究一
探究二
探究三
思维辨析
随堂演练
2.某天早上,小明骑车上学,出发时感到时间较紧,然后加速前进,后来发现时间还比较充裕,于是放慢了速度,与以上事件吻合得最好的图象是( )
解析:因为选项A,D第一段都是匀速前进,不合题意,故排除选项A,D,首先加速前进,然后放慢速度,说明图象上升的速度先快后慢,故选C.
答案:C
探究一
探究二
探究三
思维辨析
随堂演练
3.已知函数f(x),g(x)对应值如下表:
则g(f(g(-1)))的值为( )
A.1 B.0
C.-1 D.无法确定
解析:g(-1)=1,
则f(g(-1))=f(1)=0,
则g(f(g(-1)))=g(0)=-1.
答案:C
探究一
探究二
探究三
思维辨析
随堂演练
4.若一个长方体的高为80 cm,长比宽多10 cm,则这个长方体的体积y(单位:cm3)与长方体的宽x(单位:cm)之间的函数表达式是 .
解析:由题意可知,长方体的长为(x+10)cm,从而长方体的体积y=80x(x+10),x>0.
答案:y=80x(x+10),x∈(0,+∞)
探究一
探究二
探究三
思维辨析
随堂演练
5.已知函数f(x)=x2-2x(-1≤x≤2).
(1)画出f(x)的图象;
(2)根据图象写出f(x)的值域.
解:(1)f(x)的图象如图所示.
(2)观察f(x)的图象可知,f(x)图象上所有点的纵坐标的取值范围是[-1,3],故f(x)的值域是[-1,3].
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
