3.4 函数的应用(一) 课件(共39张PPT)——高中数学人教A版(2019)必修第一册
文档属性
| 名称 | 3.4 函数的应用(一) 课件(共39张PPT)——高中数学人教A版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 00:00:00 | ||
图片预览











文档简介
(共39张PPT)
人教高中A版必修一数学课件
3.4 函数的应用(一)
数学建模活动:决定苹果的最佳出售时间点
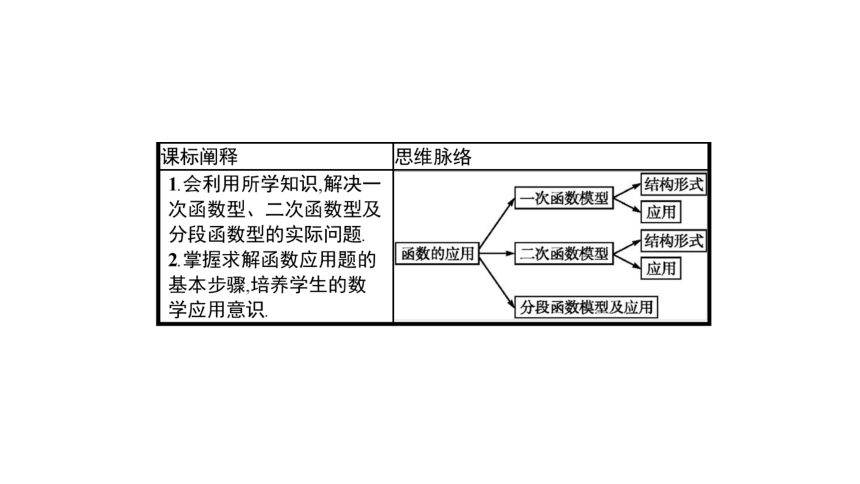
学习目标
01
一
二
知识点一、函数模型
1.思考
(1)在函数建模中,怎样确立两个变量是哪种函数关系
提示:通常需要先画出函数图像,根据图像来确定两个变量的关系,选择函数类型.
(2)函数模型在实际应用中,函数的自变量有什么特点
提示:在实际应用中,函数的自变量x往往具有实际意义,如x表示长度时,x≥0;x表示件数时,x≥0,且x∈Z等.在解答时,必须要考虑这些实际意义.
一
二
(3)已知某商场经营一批进价为12元/个的小商品,在4天的试销中,对此商品的销售单价x(元)与相应的日销售量y(个)进行了统计,其数据如下表:
你能否找到一种函数,使它反映y关于x的函数关系 若能,写出函数解析式.
一
二
提示:观察x,y的数据,可大体看到y与x是一次函数关系,
令y=kx+b(k≠0).
因为当x=16时,y=42,当x=20时,y=30,
即y=-3x+90.
显然当x=24时,y=18;当x=28时,y=6.
对照数据,可以看出y=-3x+90即为所求的函数解析式.
考虑到x的实际意义及y的取整性,所以y=-3x+90,x∈{1,2,3,…,30}.
一
二
2.填空
(1)一次函数模型
解析式:y=kx+b(k≠0).
(2)二次函数模型
①一般式:y=ax2+bx+c(a≠0);
②顶点式:y=a(x-h)2+k(a≠0),其中顶点坐标为(h,k).
(3)分段函数模型
有些实际问题,在事物的某个阶段对应的变化规律不尽相同,此时我们可以选择利用分段函数模型来刻画它,由于分段函数在不同的区间中具有不同的解析式,因此分段函数在研究条件变化的实际问题中,或者在某一特定条件下的实际问题中具有广泛的应用.
一
二
归纳提高1.在求其解析式时,应先确定分“段”,即函数分成几段,并抓住“分界点”,确保分界点“不重,不漏”.
2.在求函数值时,先确定自变量的值所属的区间,再代入;同样,已知函数值,求解自变量的值时,就是解方程的过程,即每段都令y取已知函数值,解出相应x的值,再判断是否属于所在区间.
一
二
知识点二、解决数学应用题的一般步骤
1.思考对教材例3中的“客房问题”你有什么体会 在现实问题中,有没有与它类似的问题 如果有,请举例说明.
提示:“客房问题”反映的规律性在实际生活中有很多典例,实际归结到最后,“客房问题”是一个二次函数模型的具体应用,在现实生活中的“调价问题”与其类似,其模型为:
当某类商品在销售价格为b元时,可售出a件,现欲提价,若单价每提高m元,则销售量平均减少n件,求提高多少元时销售的总收入最高
设将商品售价提高x个m元,
则总收入为y=(b+xm)·(a-xn)=-mnx2+(am-bn)x+ab.
它是一个自变量为自然数的二次函数,且其二次项系数小于零,根据二次函数的知识知它有最大值.
一
二
2.做一做
某家报刊销售点从报社买进报纸的价格是每份0.35元,卖出的价格是每份0.50元,卖不掉的报纸还可以以每份0.08元的价格退回报社,在一个月(30天)里有20天每天可以卖出报纸400份,其余10天每天只能卖出250份.若每天从报社买进报纸的数量相同,则每天应该从报社买进多少份报纸,才能使每月所获得的利润最大 并计算该销售点一个月最多可赚多少元
解:设每天应从报社买x份报纸,由题意知250≤x≤400,设每月赚y元,根据题意得y=0.5x·20+0.5×250×10+(x-250)×0.08×10-0.35x·30=0.3x+1 050,x∈[250,400].
因为y=0.3x+1 050是定义域上的增函数,所以当x=400时,ymax=120+1 050=1 170(元).
答:每天应该从报社买进400份报纸,才能使每月所获得的利润最大,每月最多可赚1 170元.
新知探究
02
探究一
探究二
探究三
思维辨析
一次函数模型的应用
例1 (1)某厂日生产文具盒的总成本y(元)与日产量x(套)之间的关系为y=6x+30 000.而出厂价格为每套12元,要使该厂不亏本,至少日生产文具盒( )
A.2 000套 B.3 000套
C.4 000套 D.5 000套
(2)商店出售茶壶和茶杯,茶壶定价为每个20元,茶杯每个5元,该商店推出两种优惠办法:
①买一个茶壶赠一个茶杯;
②按总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯x(个),付款y(元),分别建立两种优惠办法中y与x之间的函数解析式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更优惠
当堂检测
探究一
探究二
探究三
思维辨析
(1)解析:因利润z=12x-(6x+30 000),所以z=6x-30 000,由z≥0解得x≥5 000,故至少日生产文具盒5 000套.
答案:D
(2)解:由优惠办法①可得函数解析式为y1=20×4+5(x-4)=5x+60(x≥4,且x∈N).
由优惠办法②可得y2=(5x+20×4)×92%=4.6x+73.6(x≥4,且x∈N).
y1-y2=0.4x-13.6(x≥4,且x∈N),
令y1-y2=0,得x=34.
所以,当购买34个茶杯时,两种办法付款相同;
当4≤x<34时,y1当x>34时,y1>y2,优惠办法②更省钱.
当堂检测
探究一
探究二
探究三
思维辨析
反思感悟1.一次函数模型的实际应用:
一次函数模型应用时,本着“问什么,设什么,列什么”这一原则.
2.一次函数的最值求解:
一次函数求最值,常转化为求解不等式ax+b≥0(或≤0),解答时,注意系数a的正负,也可以结合函数图像或其单调性来求最值.
当堂检测
探究一
探究二
探究三
思维辨析
变式训练1若一根蜡烛长20 cm,点燃后每小时燃烧5 cm,则燃烧剩下的高度h(cm)与燃烧时间t(h)的函数关系用图像表示为图中的( )
解析:蜡烛剩下的长度随时间增加而缩短,根据实际意义不可能是D,更不可能是A,C.故选B.
答案:B
当堂检测
探究一
探究二
探究三
思维辨析
二次函数模型的应用
例2 某水果批发商销售每箱进价为40元的苹果,假设每箱售价不得低于50元且不得高于55元.市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天的销售量y(箱)与销售单价x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润w(元)与销售单价x(元/箱)之间的函数关系式;
(3)当每箱苹果的售价为多少元时,可以获得最大利润 最大利润是多少
当堂检测
探究一
探究二
探究三
思维辨析
分析:本题中平均每天的销售量y(箱)与销售单价x(元/箱)是一个一次函数关系,虽然x∈[50,55],x∈N,但仍可把问题看成一次函数模型的应用问题;平均每天的销售利润w(元)与销售单价x(元/箱)是一个二次函数关系,可看成是一个二次函数模型的应用题.
解:(1)根据题意,得y=90-3(x-50),
化简,得y=-3x+240(50≤x≤55,x∈N).
(2)因为该批发商平均每天的销售利润=平均每天的销售量×每箱销售利润.
所以w=(x-40)(-3x+240)=-3x2+360x-9 600(50≤x≤55,x∈N).
(3)因为w=-3x2+360x-9 600=-3(x-60)2+1 200,
所以当x<60时,w随x的增大而增大.
又50≤x≤55,x∈N,所以当x=55时,w有最大值,最大值为1 125.
所以当每箱苹果的售价为55元时,可以获得最大利润,且最大利润为1 125元.
当堂检测
探究一
探究二
探究三
思维辨析
反思感悟二次函数的实际应用
1.在根据实际问题建立函数解析式后,可利用配方法、判别式法、换元法、函数的单调性等方法来求函数的最值,从而解决实际问题中的最值问题.二次函数求最值最好结合二次函数的图像来解答.
2.对于本题要清楚平均每天的销售利润=平均每天的销售量×每箱销售利润.
当堂检测
探究一
探究二
探究三
思维辨析
变式训练2有A,B两城相距100 km,在A,B两城之间距A城x km的D地建一核电站给这两城供电.为保证城市安全,核电站与城市距离不得少于10 km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数λ=0.25.若A城供电量为20亿度/月,B城供电量为10亿度/月.
(1)把月供电总费用y表示成x的函数,并求定义域;
(2)核电站建在距A城多远时,才能使供电费用最小
当堂检测
探究一
探究二
探究三
思维辨析
分段函数模型的应用
例3 WAP手机上网每月使用量在500 min以下(包括500 min),按30元计费;超过500 min的部分按0.15元/min计费.假如上网时间过短(小于60 min)使用量在1 min以下不计费,在1 min以上(包括1 min)按0.5元/min计费.WAP手机上网不收通话费和漫游费.
(1)写出上网时间x min与所付费用y元之间的函数关系式.
(2)12月份小王WAP上网使用量为20 h,要付多少钱
(3)小王10月份付了90元的WAP上网费,那么他上网的时间是多少
分析:由于上网时间不同,收费标准不同,因此对所付费用作分段讨论,以确定付费标准,建立函数关系式,解决付费与上网时间的问题.
当堂检测
探究一
探究二
探究三
思维辨析
解:(1)设上网时间为x min,由已知条件所付费用y关于x的函数关系式为
(2)当x=20×60=1 200(min)时,x>500,应付y=30+0.15×(1 200-500)=135(元).
(3)90元已超过30元,所以上网时间超过500 min,由解析式可得上网时间为900 min.
当堂检测
探究一
探究二
探究三
思维辨析
反思感悟分段函数的实际应用
1.在刻画实际问题中,变量之间的关系因自变量x取值范围的不同,对应的函数关系不能用同一个解析式表示时,常用分段函数建立函数模型解决问题.
2.分段函数是指自变量在不同的范围内有着不同对应法则的函数.求解分段函数的最值问题时应注意:分段函数的最大值是各段函数最大值中较大的一个,分段函数的最小值是各段函数最小值中较小的一个.
当堂检测
探究一
探究二
探究三
思维辨析
延伸探究为支持福利事业,解决残疾人就业问题,银行决定给某福利企业免息贷款46.8万元,用于经营某种商品.已知该种商品的进价为每件40元,每月销售量q(单位:百件)与销售价p(单位:元/件)之间满足关系式: 该企业职工每人每月工资为1 200元,其他经营性费用为每月13 200元.
(1)如果暂时不考虑还贷的前提下,当销售价p为52元/件,每月刚好收支平衡,求该企业的职工人数;
(2)若该企业只有20名职工,在保证职工工资及其他经营性支出外,剩余的利润都用来偿还贷款,试问最早几年后还清贷款
当堂检测
探究一
探究二
探究三
思维辨析
解:(1)设该企业职工人数为t,依题意当p=52时,q=36,则(52-40)×36×100=1 200t+13 200,∴t=25.
即该企业有25名职工.
(2)设每个月的利润为f(p),则f(p)=
∵当p=55时,[(-2p+140)(p-40)]max=450,
当p=61时,[(-p+82)(p-40)]max=441,
∵450>441,
∴当p=55时,能更早还清贷款,
又(100×450-1 200×20-13 200)×12=93 600,
∴当定价为55元时,最早5年后能还清贷款.
当堂检测
巩固练习
03
探究一
探究二
探究三
思维辨析
因忽视实际问题中x的范围而致误
典例 如图所示,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB,AD,CB,CD上分别截取AE=AH=CF=CG=x(x>0),设四边形EFGH的面积为y.
(1)写出四边形EFGH的面积y与x之间的函数关系式;
(2)求当x为何值时,y取得最大值,最大值是多少
当堂检测
探究一
探究二
探究三
思维辨析
当堂检测
探究一
探究二
探究三
思维辨析
以上解答过程中都有哪些错误 出错的原因是什么 你如何订正 你怎么防范
提示:错解过程中一是没注意实际问题中x的取值范围,二是求函数最值时没有讨论对称轴与区间的关系,但从根本上错误的根源是第(1)问中没有明确定义域.
当堂检测
探究一
探究二
探究三
思维辨析
当堂检测
探究一
探究二
探究三
思维辨析
防范措施1.对实际问题中的函数解析式一定要注意自变量x要受实际问题的约束,养成遇到实际问题“定义域优先”的习惯.
2.有时一个小细节的失误,会导致严重错误的产生.因此解决实际问题时,要充分考虑问题的背景、实际意义、隐含条件等.
当堂检测
探究一
探究二
探究三
思维辨析
变式训练某企业实行裁员增效.已知现有员工a人,每人每年可创纯收益(已扣工资等)1万元,据评估,在生产条件不变的条件下,每裁员一人,则留岗人员每人每年可多创收0.01万元,但每年需付给每位下岗工人0.4万元生活费,并且企业正常运转所需人数不得少于现有员工的 ,设该企业裁员x人后年纯收益为y万元.
(1)写出y关于x的函数解析式,并指出x的取值范围;
(2)当140当堂检测
探究一
探究二
探究三
思维辨析
当堂检测
拓展延伸
04
探究一
探究二
探究三
思维辨析
当堂检测
1.一个等腰三角形的周长是20,则底边长y是关于腰长x的函数,其解析式为( )
A.y=20-2x(x≤10) B.y=20-2x(x<10)
C.y=20-2x(5≤x≤10) D.y=20-2x(5答案:D
探究一
探究二
探究三
思维辨析
当堂检测
2.某生产厂家的生产总成本y(万元)与产量x(件)之间的关系式为y=x2-80x,若每件产品的售价为25万元,则该厂获得最大利润时,生产的产品件数为( )
A.52 B.52.5 C.53 D.52或53
解析:因为利润=收入-成本,当产量为x件时(x∈N),利润f(x)=25x-(x2-80x),
所以x=52或x=53时,f(x)有最大值.
答案:D
探究一
探究二
探究三
思维辨析
当堂检测
3.某商店进货单价为45元,若按50元一个销售,能卖出50个;若销售单价每涨1元,其销售量就减少2个,为了获得最大利润,此商品的最佳售价应为每个 元.
解析:设涨价x元,销售的利润为y元,
则y=(50+x-45)(50-2x)=-2x2+40x+250=-2(x-10)2+450,
所以当x=10,即销售价为60元时,y取得最大值.
答案:60
探究一
探究二
探究三
思维辨析
当堂检测
4.已知直角梯形ABCD,如图(1)所示,动点P从点B出发,由B→C→D→A沿边运动,设点P运动的路程为x,△ABP的面积为f(x).如果函数y=f(x)的图像如图(2)所示,则△ABC的面积为 .
解析:由题中图像可知BC=4,CD=5,DA=5,
答案:16
探究一
探究二
探究三
思维辨析
当堂检测
5.南博汽车城销售某种型号的汽车,进货单价为每辆25万元,市场调研表明:当销售单价为每辆29万元时,平均每周能售出8辆,而当销售单价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元(每辆车的销售利润=销售单价-进货单价).
(1)求y与x之间的函数关系式,并在保证商家不亏本的前提下,写出x的取值范围;
(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3)当每辆汽车的销售单价为多少万元时,平均每周的销售利润最大 最大利润是多少
探究一
探究二
探究三
思维辨析
当堂检测
解:(1)因为y=29-25-x,所以y=-x+4(0≤x≤4,x=0.5n,n∈N).
(0≤x≤4,x=0.5n,n∈N).
(3)由(2)知,z=-8x2+24x+32=-8(x-1.5)2+50(0≤x≤4,x=0.5n,n∈N),故当x=1.5时,zmax=50.
所以当销售单价为每辆29-1.5=27.5(万元)时,每周的销售利润最大,最大利润为50万元.
人教高中A版必修一数学课件
3.4 函数的应用(一)
数学建模活动:决定苹果的最佳出售时间点
学习目标
01
一
二
知识点一、函数模型
1.思考
(1)在函数建模中,怎样确立两个变量是哪种函数关系
提示:通常需要先画出函数图像,根据图像来确定两个变量的关系,选择函数类型.
(2)函数模型在实际应用中,函数的自变量有什么特点
提示:在实际应用中,函数的自变量x往往具有实际意义,如x表示长度时,x≥0;x表示件数时,x≥0,且x∈Z等.在解答时,必须要考虑这些实际意义.
一
二
(3)已知某商场经营一批进价为12元/个的小商品,在4天的试销中,对此商品的销售单价x(元)与相应的日销售量y(个)进行了统计,其数据如下表:
你能否找到一种函数,使它反映y关于x的函数关系 若能,写出函数解析式.
一
二
提示:观察x,y的数据,可大体看到y与x是一次函数关系,
令y=kx+b(k≠0).
因为当x=16时,y=42,当x=20时,y=30,
即y=-3x+90.
显然当x=24时,y=18;当x=28时,y=6.
对照数据,可以看出y=-3x+90即为所求的函数解析式.
考虑到x的实际意义及y的取整性,所以y=-3x+90,x∈{1,2,3,…,30}.
一
二
2.填空
(1)一次函数模型
解析式:y=kx+b(k≠0).
(2)二次函数模型
①一般式:y=ax2+bx+c(a≠0);
②顶点式:y=a(x-h)2+k(a≠0),其中顶点坐标为(h,k).
(3)分段函数模型
有些实际问题,在事物的某个阶段对应的变化规律不尽相同,此时我们可以选择利用分段函数模型来刻画它,由于分段函数在不同的区间中具有不同的解析式,因此分段函数在研究条件变化的实际问题中,或者在某一特定条件下的实际问题中具有广泛的应用.
一
二
归纳提高1.在求其解析式时,应先确定分“段”,即函数分成几段,并抓住“分界点”,确保分界点“不重,不漏”.
2.在求函数值时,先确定自变量的值所属的区间,再代入;同样,已知函数值,求解自变量的值时,就是解方程的过程,即每段都令y取已知函数值,解出相应x的值,再判断是否属于所在区间.
一
二
知识点二、解决数学应用题的一般步骤
1.思考对教材例3中的“客房问题”你有什么体会 在现实问题中,有没有与它类似的问题 如果有,请举例说明.
提示:“客房问题”反映的规律性在实际生活中有很多典例,实际归结到最后,“客房问题”是一个二次函数模型的具体应用,在现实生活中的“调价问题”与其类似,其模型为:
当某类商品在销售价格为b元时,可售出a件,现欲提价,若单价每提高m元,则销售量平均减少n件,求提高多少元时销售的总收入最高
设将商品售价提高x个m元,
则总收入为y=(b+xm)·(a-xn)=-mnx2+(am-bn)x+ab.
它是一个自变量为自然数的二次函数,且其二次项系数小于零,根据二次函数的知识知它有最大值.
一
二
2.做一做
某家报刊销售点从报社买进报纸的价格是每份0.35元,卖出的价格是每份0.50元,卖不掉的报纸还可以以每份0.08元的价格退回报社,在一个月(30天)里有20天每天可以卖出报纸400份,其余10天每天只能卖出250份.若每天从报社买进报纸的数量相同,则每天应该从报社买进多少份报纸,才能使每月所获得的利润最大 并计算该销售点一个月最多可赚多少元
解:设每天应从报社买x份报纸,由题意知250≤x≤400,设每月赚y元,根据题意得y=0.5x·20+0.5×250×10+(x-250)×0.08×10-0.35x·30=0.3x+1 050,x∈[250,400].
因为y=0.3x+1 050是定义域上的增函数,所以当x=400时,ymax=120+1 050=1 170(元).
答:每天应该从报社买进400份报纸,才能使每月所获得的利润最大,每月最多可赚1 170元.
新知探究
02
探究一
探究二
探究三
思维辨析
一次函数模型的应用
例1 (1)某厂日生产文具盒的总成本y(元)与日产量x(套)之间的关系为y=6x+30 000.而出厂价格为每套12元,要使该厂不亏本,至少日生产文具盒( )
A.2 000套 B.3 000套
C.4 000套 D.5 000套
(2)商店出售茶壶和茶杯,茶壶定价为每个20元,茶杯每个5元,该商店推出两种优惠办法:
①买一个茶壶赠一个茶杯;
②按总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯x(个),付款y(元),分别建立两种优惠办法中y与x之间的函数解析式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更优惠
当堂检测
探究一
探究二
探究三
思维辨析
(1)解析:因利润z=12x-(6x+30 000),所以z=6x-30 000,由z≥0解得x≥5 000,故至少日生产文具盒5 000套.
答案:D
(2)解:由优惠办法①可得函数解析式为y1=20×4+5(x-4)=5x+60(x≥4,且x∈N).
由优惠办法②可得y2=(5x+20×4)×92%=4.6x+73.6(x≥4,且x∈N).
y1-y2=0.4x-13.6(x≥4,且x∈N),
令y1-y2=0,得x=34.
所以,当购买34个茶杯时,两种办法付款相同;
当4≤x<34时,y1
当堂检测
探究一
探究二
探究三
思维辨析
反思感悟1.一次函数模型的实际应用:
一次函数模型应用时,本着“问什么,设什么,列什么”这一原则.
2.一次函数的最值求解:
一次函数求最值,常转化为求解不等式ax+b≥0(或≤0),解答时,注意系数a的正负,也可以结合函数图像或其单调性来求最值.
当堂检测
探究一
探究二
探究三
思维辨析
变式训练1若一根蜡烛长20 cm,点燃后每小时燃烧5 cm,则燃烧剩下的高度h(cm)与燃烧时间t(h)的函数关系用图像表示为图中的( )
解析:蜡烛剩下的长度随时间增加而缩短,根据实际意义不可能是D,更不可能是A,C.故选B.
答案:B
当堂检测
探究一
探究二
探究三
思维辨析
二次函数模型的应用
例2 某水果批发商销售每箱进价为40元的苹果,假设每箱售价不得低于50元且不得高于55元.市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天的销售量y(箱)与销售单价x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润w(元)与销售单价x(元/箱)之间的函数关系式;
(3)当每箱苹果的售价为多少元时,可以获得最大利润 最大利润是多少
当堂检测
探究一
探究二
探究三
思维辨析
分析:本题中平均每天的销售量y(箱)与销售单价x(元/箱)是一个一次函数关系,虽然x∈[50,55],x∈N,但仍可把问题看成一次函数模型的应用问题;平均每天的销售利润w(元)与销售单价x(元/箱)是一个二次函数关系,可看成是一个二次函数模型的应用题.
解:(1)根据题意,得y=90-3(x-50),
化简,得y=-3x+240(50≤x≤55,x∈N).
(2)因为该批发商平均每天的销售利润=平均每天的销售量×每箱销售利润.
所以w=(x-40)(-3x+240)=-3x2+360x-9 600(50≤x≤55,x∈N).
(3)因为w=-3x2+360x-9 600=-3(x-60)2+1 200,
所以当x<60时,w随x的增大而增大.
又50≤x≤55,x∈N,所以当x=55时,w有最大值,最大值为1 125.
所以当每箱苹果的售价为55元时,可以获得最大利润,且最大利润为1 125元.
当堂检测
探究一
探究二
探究三
思维辨析
反思感悟二次函数的实际应用
1.在根据实际问题建立函数解析式后,可利用配方法、判别式法、换元法、函数的单调性等方法来求函数的最值,从而解决实际问题中的最值问题.二次函数求最值最好结合二次函数的图像来解答.
2.对于本题要清楚平均每天的销售利润=平均每天的销售量×每箱销售利润.
当堂检测
探究一
探究二
探究三
思维辨析
变式训练2有A,B两城相距100 km,在A,B两城之间距A城x km的D地建一核电站给这两城供电.为保证城市安全,核电站与城市距离不得少于10 km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数λ=0.25.若A城供电量为20亿度/月,B城供电量为10亿度/月.
(1)把月供电总费用y表示成x的函数,并求定义域;
(2)核电站建在距A城多远时,才能使供电费用最小
当堂检测
探究一
探究二
探究三
思维辨析
分段函数模型的应用
例3 WAP手机上网每月使用量在500 min以下(包括500 min),按30元计费;超过500 min的部分按0.15元/min计费.假如上网时间过短(小于60 min)使用量在1 min以下不计费,在1 min以上(包括1 min)按0.5元/min计费.WAP手机上网不收通话费和漫游费.
(1)写出上网时间x min与所付费用y元之间的函数关系式.
(2)12月份小王WAP上网使用量为20 h,要付多少钱
(3)小王10月份付了90元的WAP上网费,那么他上网的时间是多少
分析:由于上网时间不同,收费标准不同,因此对所付费用作分段讨论,以确定付费标准,建立函数关系式,解决付费与上网时间的问题.
当堂检测
探究一
探究二
探究三
思维辨析
解:(1)设上网时间为x min,由已知条件所付费用y关于x的函数关系式为
(2)当x=20×60=1 200(min)时,x>500,应付y=30+0.15×(1 200-500)=135(元).
(3)90元已超过30元,所以上网时间超过500 min,由解析式可得上网时间为900 min.
当堂检测
探究一
探究二
探究三
思维辨析
反思感悟分段函数的实际应用
1.在刻画实际问题中,变量之间的关系因自变量x取值范围的不同,对应的函数关系不能用同一个解析式表示时,常用分段函数建立函数模型解决问题.
2.分段函数是指自变量在不同的范围内有着不同对应法则的函数.求解分段函数的最值问题时应注意:分段函数的最大值是各段函数最大值中较大的一个,分段函数的最小值是各段函数最小值中较小的一个.
当堂检测
探究一
探究二
探究三
思维辨析
延伸探究为支持福利事业,解决残疾人就业问题,银行决定给某福利企业免息贷款46.8万元,用于经营某种商品.已知该种商品的进价为每件40元,每月销售量q(单位:百件)与销售价p(单位:元/件)之间满足关系式: 该企业职工每人每月工资为1 200元,其他经营性费用为每月13 200元.
(1)如果暂时不考虑还贷的前提下,当销售价p为52元/件,每月刚好收支平衡,求该企业的职工人数;
(2)若该企业只有20名职工,在保证职工工资及其他经营性支出外,剩余的利润都用来偿还贷款,试问最早几年后还清贷款
当堂检测
探究一
探究二
探究三
思维辨析
解:(1)设该企业职工人数为t,依题意当p=52时,q=36,则(52-40)×36×100=1 200t+13 200,∴t=25.
即该企业有25名职工.
(2)设每个月的利润为f(p),则f(p)=
∵当p=55时,[(-2p+140)(p-40)]max=450,
当p=61时,[(-p+82)(p-40)]max=441,
∵450>441,
∴当p=55时,能更早还清贷款,
又(100×450-1 200×20-13 200)×12=93 600,
∴当定价为55元时,最早5年后能还清贷款.
当堂检测
巩固练习
03
探究一
探究二
探究三
思维辨析
因忽视实际问题中x的范围而致误
典例 如图所示,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB,AD,CB,CD上分别截取AE=AH=CF=CG=x(x>0),设四边形EFGH的面积为y.
(1)写出四边形EFGH的面积y与x之间的函数关系式;
(2)求当x为何值时,y取得最大值,最大值是多少
当堂检测
探究一
探究二
探究三
思维辨析
当堂检测
探究一
探究二
探究三
思维辨析
以上解答过程中都有哪些错误 出错的原因是什么 你如何订正 你怎么防范
提示:错解过程中一是没注意实际问题中x的取值范围,二是求函数最值时没有讨论对称轴与区间的关系,但从根本上错误的根源是第(1)问中没有明确定义域.
当堂检测
探究一
探究二
探究三
思维辨析
当堂检测
探究一
探究二
探究三
思维辨析
防范措施1.对实际问题中的函数解析式一定要注意自变量x要受实际问题的约束,养成遇到实际问题“定义域优先”的习惯.
2.有时一个小细节的失误,会导致严重错误的产生.因此解决实际问题时,要充分考虑问题的背景、实际意义、隐含条件等.
当堂检测
探究一
探究二
探究三
思维辨析
变式训练某企业实行裁员增效.已知现有员工a人,每人每年可创纯收益(已扣工资等)1万元,据评估,在生产条件不变的条件下,每裁员一人,则留岗人员每人每年可多创收0.01万元,但每年需付给每位下岗工人0.4万元生活费,并且企业正常运转所需人数不得少于现有员工的 ,设该企业裁员x人后年纯收益为y万元.
(1)写出y关于x的函数解析式,并指出x的取值范围;
(2)当140
探究一
探究二
探究三
思维辨析
当堂检测
拓展延伸
04
探究一
探究二
探究三
思维辨析
当堂检测
1.一个等腰三角形的周长是20,则底边长y是关于腰长x的函数,其解析式为( )
A.y=20-2x(x≤10) B.y=20-2x(x<10)
C.y=20-2x(5≤x≤10) D.y=20-2x(5
探究一
探究二
探究三
思维辨析
当堂检测
2.某生产厂家的生产总成本y(万元)与产量x(件)之间的关系式为y=x2-80x,若每件产品的售价为25万元,则该厂获得最大利润时,生产的产品件数为( )
A.52 B.52.5 C.53 D.52或53
解析:因为利润=收入-成本,当产量为x件时(x∈N),利润f(x)=25x-(x2-80x),
所以x=52或x=53时,f(x)有最大值.
答案:D
探究一
探究二
探究三
思维辨析
当堂检测
3.某商店进货单价为45元,若按50元一个销售,能卖出50个;若销售单价每涨1元,其销售量就减少2个,为了获得最大利润,此商品的最佳售价应为每个 元.
解析:设涨价x元,销售的利润为y元,
则y=(50+x-45)(50-2x)=-2x2+40x+250=-2(x-10)2+450,
所以当x=10,即销售价为60元时,y取得最大值.
答案:60
探究一
探究二
探究三
思维辨析
当堂检测
4.已知直角梯形ABCD,如图(1)所示,动点P从点B出发,由B→C→D→A沿边运动,设点P运动的路程为x,△ABP的面积为f(x).如果函数y=f(x)的图像如图(2)所示,则△ABC的面积为 .
解析:由题中图像可知BC=4,CD=5,DA=5,
答案:16
探究一
探究二
探究三
思维辨析
当堂检测
5.南博汽车城销售某种型号的汽车,进货单价为每辆25万元,市场调研表明:当销售单价为每辆29万元时,平均每周能售出8辆,而当销售单价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元(每辆车的销售利润=销售单价-进货单价).
(1)求y与x之间的函数关系式,并在保证商家不亏本的前提下,写出x的取值范围;
(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3)当每辆汽车的销售单价为多少万元时,平均每周的销售利润最大 最大利润是多少
探究一
探究二
探究三
思维辨析
当堂检测
解:(1)因为y=29-25-x,所以y=-x+4(0≤x≤4,x=0.5n,n∈N).
(0≤x≤4,x=0.5n,n∈N).
(3)由(2)知,z=-8x2+24x+32=-8(x-1.5)2+50(0≤x≤4,x=0.5n,n∈N),故当x=1.5时,zmax=50.
所以当销售单价为每辆29-1.5=27.5(万元)时,每周的销售利润最大,最大利润为50万元.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
