4.5.2 函数的最大(小)值 课件(共33张PPT)——高中数学人教A版(2019)必修第一册
文档属性
| 名称 | 4.5.2 函数的最大(小)值 课件(共33张PPT)——高中数学人教A版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 16:58:01 | ||
图片预览









文档简介
(共33张PPT)
人教高中A版必修一数学课件
第2课时 函数的最大(小)值
学习目标
01
新知探究
02
一
二
一、函数的最大(小)值的定义
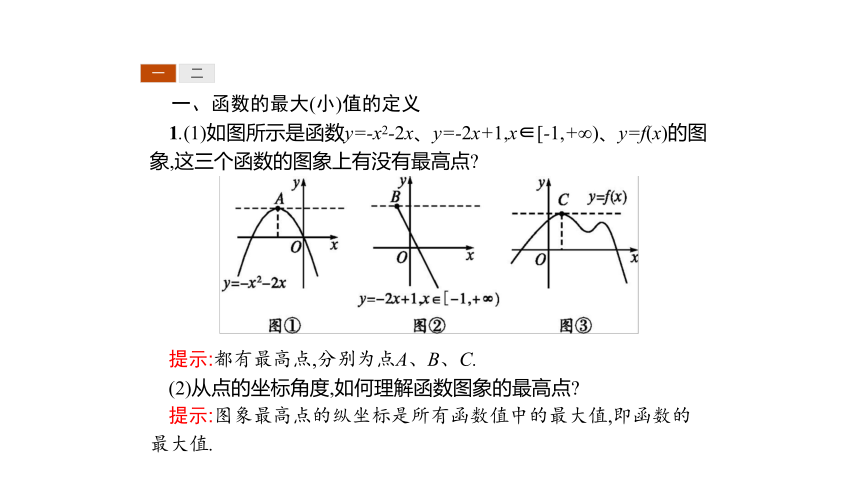
1.(1)如图所示是函数y=-x2-2x、y=-2x+1,x∈[-1,+∞)、y=f(x)的图象,这三个函数的图象上有没有最高点
提示:都有最高点,分别为点A、B、C.
(2)从点的坐标角度,如何理解函数图象的最高点
提示:图象最高点的纵坐标是所有函数值中的最大值,即函数的最大值.
一
二
(3)如图③所示,图象上最高点C的坐标为(x0,f(x0)),在图象上任取一点A(x,f(x)),f(x)与f(x0)有什么关系
提示:点C是图象的最高点,即对定义域内任意x,均有f(x)≤f(x0)成立.
(4)一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:①对 x∈I,都有f(x)≤M;
② x0∈I,使得f(x0)=M,那么我们就称M是函数y=f(x)的最大值.
其几何意义:函数y=f(x)的最大值是图象最高点的纵坐标.
(5)类比函数最大值的定义,请你给出最小值的定义及其几何意义.
提示:一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
① x∈I,都有f(x)≥M;
② x0∈I,使得f(x0)=M.那么,称M是函数y=f(x)的最小值.
函数最小值的几何意义:函数图象上最低点的纵坐标.
一
二
(6)是否每个函数都有最大值、最小值 如果有最值,取最值的点有几个 举例说明.
提示:一个函数不一定有最值,例如y= 在定义域内没有最大值也没有最小值.有的函数可能只有一个最大(或小)值,例如y=-2x+1,x∈[-1,+∞).如果一个函数存在最值,那么函数的最大值和最小值都是唯一的,但取最值时的自变量可以有多个,如y=x2,x∈[-2,2],最大值只有一个为4,而取最大值的x有x=±2两个.
一
二
2.做一做
已知函数f(x)在[-2,2]上的图象如图所示,则该函数的最小值、最大值分别是( )
A.f(-2),0 B.0,2
C.f(-2),2 D.f(2),2
解析:由题图可知,该函数的最小值为f(-2),最大值为f(1)=2.
答案:C
一
二
二、函数的单调性与最大(小)值
1.(1)若函数y=f(x)在区间[a,b]上是增函数或减函数,它一定有最值吗 如果有,最值是什么
提示:若函数y=f(x)在区间[a,b]上是增函数,则函数的最小值为ymin=f(a),最大值为ymax=f(b);若函数y=f(x)在区间[a,b]上是减函数,则函数的最小值为ymin=f(b),最大值为ymax=f(a).
(2)若函数y=f(x)在区间(a,b)上是增(或减)函数,这个函数有最值吗
活动方案:启发学生画一个符合条件的函数草图,注意端点不在区间内,然后回答.
提示:不存在最值,但可以说函数y=f(x)在区间(a,b)上的值域为(f(a),f(b))[或(f(b),f(a))].
一
二
(3)已知函数y=f(x)的定义域是[a,b],a提示:因为当x∈[a,c]时,f(x)是单调增函数,所以对于任意x∈[a,c],都有f(x)≤f(c).又因为当x∈[c,b]时,f(x)是单调减函数,所以对于任意x∈[c,b],都有f(x)≤f(c).因此,对于任意x∈[a,b]都有f(x)≤f(c),即f(x)在x=c时取得最大值.
2.做一做
函数y=x2-4x+1在[-2,0]上的最大值是 ,最小值是 .
解析:函数y=x2-4x+1在[-2,0]上单调递减,故当x=2时,ymax=13,当x=0时,ymin=1.
答案:13 1
探究一
探究二
探究三
思想方法
随堂演练
利用函数的图象求函数的最值
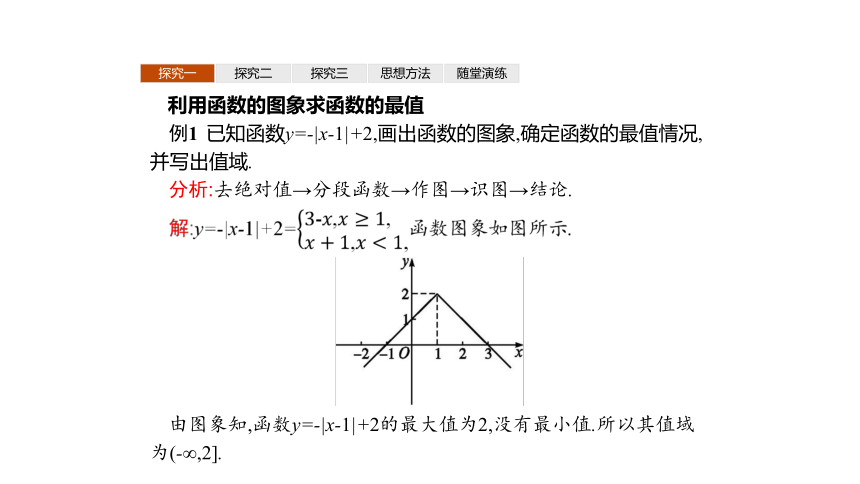
例1 已知函数y=-|x-1|+2,画出函数的图象,确定函数的最值情况,并写出值域.
分析:去绝对值→分段函数→作图→识图→结论.
由图象知,函数y=-|x-1|+2的最大值为2,没有最小值.所以其值域为(-∞,2].
探究一
探究二
探究三
思想方法
随堂演练
反思感悟
探究一
探究二
探究三
思想方法
随堂演练
(1)画出f(x)的图象;
(2)利用图象写出该函数的最大值和最小值.
解:(1)函数f(x)的图象如图所示.
(2)由图象可知f(x)的最小值为f(1)=1,无最大值.
探究一
探究二
探究三
思想方法
随堂演练
利用函数的单调性求最值
例2 已知函数f(x)=x+ .
(1)判断f(x)在区间[1,2]上的单调性;
(2)根据f(x)的单调性求出f(x)在区间[1,2]上的最值.
分析:(1)证明单调性的流程:取值→作差→变形→判断符号→结论;
(2)借助最值与单调性的关系,写出最值.
探究一
探究二
探究三
思想方法
随堂演练
∵x10,1∴f(x1)>f(x2),即f(x)在区间[1,2]上是减函数.
(2)由(1)知f(x)的最小值为f(2),f(2)=2+ =4;f(x)的最大值为f(1).
∵f(1)=1+4=5,∴f(x)的最小值为4,最大值为5.
探究一
探究二
探究三
思想方法
随堂演练
反思感悟 1.利用单调性求函数最值的一般步骤:
(1)判断函数的单调性;(2)利用单调性写出最值.
2.函数的最值与单调性的关系:
(1)若函数f(x)在区间[a,b]上是增(减)函数,则f(x)在区间[a,b]上的最小(大)值是f(a),最大(小)值是f(b).
(2)若函数f(x)在区间[a,b]上是增(减)函数,在区间(b,c]上是减(增)函数,则f(x)在区间[a,c]上的最大(小)值是f(b),最小(大)值是f(a)与f(c)中较小(大)的一个.
(3)若函数f(x)在区间[a,b]上的图象是一条连续不断的曲线,则函数f(x)在区间[a,b]上一定有最值.
(4)求最值时一定要注意所给区间的开闭,若是开区间,则不一定有最大(小)值.
探究一
探究二
探究三
思想方法
随堂演练
延伸探究本例已知条件不变,判断f(x)在区间[1,3]上的单调性,并求f(x)在区间[1,3]上的最值.
当1≤x1f(x2),f(x)在区间[1,2]上为减函数;
当20,40,∴f(x1)探究一
探究二
探究三
思想方法
随堂演练
与最值有关的应用问题
例3 某租赁公司拥有汽车100辆,当每辆车的月租金为3 000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金为3 600元时,能租出多少辆
(2)当每辆车的月租金为多少元时,租赁公司的月收益最大 最大月收益是多少
分析:读题→提取信息→建模→解模→解决实际问题
探究一
探究二
探究三
思想方法
随堂演练
解:(1)当每辆车的月租金为3 600元时,
所以当x=4 050,即每辆车的租金为4 050元时,租赁公司的月收益最大,最大月收益是307 050元.
探究一
探究二
探究三
思想方法
随堂演练
反思感悟 1.本题建立的是二次函数模型,应利用配方法求函数的最值.
2.解函数应用题的一般程序是:
(1)审题.弄清题意,分清条件和结论,理顺数量关系.
(2)建模.将文字语言转化成数学语言,用数学知识建立相应的数学模型.
(3)求模.求解数学模型,得到数学结论.
(4)还原.将用数学方法得到的结论还原为实际问题的意义.
(5)反思回顾.对于数学模型得到的数学解,必须验证这个数学解对实际问题的合理性.
探究一
探究二
探究三
思想方法
随堂演练
变式训练2某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需增加投入100元,已知总收益满足函数:
解:(1)设月产量为x台,则总成本为20 000+100x,
∴当x=300时,f(x)max=25 000,
当x>400时,f(x)=60 000-100x是减函数,
f(x)<60 000-100×400<25 000.∴当x=300时,f(x)max=25 000.
即每月生产300台仪器时利润最大,最大利润为25 000元.
巩固练习
03
探究一
探究二
探究三
思想方法
随堂演练
利用数形结合思想与分类讨论思想求二次函数的最值
典例 求函数y=x2-2ax-1在区间[0,2]上的最值.
【审题视角】可变对称轴x=a→与定区间[0,2]的
相对位置关系→结合单调性与图象求解
解:y=(x-a)2-1-a2.
当a<0时,[0,2]是函数的递增区间,如图①.
故函数在x=0处取得最小值-1,
在x=2处取得最大值3-4a.
当0≤a≤1时,结合函数图象(如图②)知,
函数在x=a处取得最小值-a2-1,
在x=2处取得最大值3-4a.
探究一
探究二
探究三
思想方法
随堂演练
当1函数在x=a处取得最小值-a2-1,
在x=0处取得最大值-1.
当a>2时,[0,2]是函数的递减区间,如图④.
函数在x=0处取得最大值-1,在x=2处取得最小值3-4a.
综上,当a<0时,函数在区间[0,2]上的最小值为-1,最大值为3-4a;
当0≤a≤1时,函数在区间[0,2]上的最小值为-a2-1,最大值为3-4a;
当1当a>2时,函数在区间[0,2]上的最小值为3-4a,最大值为-1.
探究一
探究二
探究三
思想方法
随堂演练
方法点睛 1.探求二次函数在给定区间上的最值问题,一般要先作出y=f(x)的草图,再根据图象的增减性进行研究.特别要注意二次函数图象的对称轴与所给区间的位置关系,它是求解二次函数在已知区间上最值问题的主要依据.二次函数图象的对称轴与所给区间的位置关系通常有三种:(1)对称轴在所给区间的右侧;(2)对称轴在所给区间的左侧;(3)对称轴在所给区间内.
探究一
探究二
探究三
思想方法
随堂演练
2.对于二次函数f(x)=a(x-h)2+k(a>0)在区间[m,n]上的最值可作如下讨论:
探究一
探究二
探究三
思想方法
随堂演练
变式训练函数f(x)=x2-2x+2(其中x∈[t,t+1],t∈R)的最小值为g(t),求g(t)的表达式.
解:由函数f(x)=x2-2x+2知其图象的开口向上,对称轴为x=1.下面分三种情况讨论:
图①
当t+1≤1,即t≤0时,如图①所示,此时函数f(x)在[t,t+1]上为减函数,∴g(t)=f(t+1)=(t+1)2-2(t+1)+2=t2+1.
探究一
探究二
探究三
思想方法
随堂演练
如图②所示,此时,函数f(x)在[t,1]上为减函数,
在(1,t+1]上为增函数,
∴g(t)=f(1)=1.
当t≥1时,如图③所示,此时,函数f(x)在[t,t+1]上为增函数,
∴g(t)=f(t)=t2-2t+2.
拓展延伸
04
探究一
探究二
探究三
思想方法
随堂演练
答案:A
2.函数y=|x+1|+2的最小值是( )
A.0 B.-1 C.2 D.3
解析:y=|x+1|+2的图象如图所示.
由图可知函数的最小值为2.
答案:C
探究一
探究二
探究三
思想方法
随堂演练
3.函数y=x2-2x,x∈[0,3]的值域为( )
A.[0,3] B.[-1,0]
C.[-1,+∞) D.[-1,3]
解析:∵函数y=x2-2x=(x-1)2-1,x∈[0,3],∴当x=1时,函数y取得最小值为-1,当x=3时,函数取得最大值为3,故函数的值域为[-1,3],故选D.
答案:D
解析:当x∈[1,2]时,f(x)为增函数,其最大值为f(2)=10;当x∈[-4,1]时,f(x)为减函数,其最大值为f(-4)=11.故函数f(x)的最大值为11.
答案:11
探究一
探究二
探究三
思想方法
随堂演练
5.把长为12 cm的细铁丝截成两段,各自围成一个正方形,求这两个正方形面积之和的最小值.
人教高中A版必修一数学课件
第2课时 函数的最大(小)值
人教高中A版必修一数学课件
第2课时 函数的最大(小)值
学习目标
01
新知探究
02
一
二
一、函数的最大(小)值的定义
1.(1)如图所示是函数y=-x2-2x、y=-2x+1,x∈[-1,+∞)、y=f(x)的图象,这三个函数的图象上有没有最高点
提示:都有最高点,分别为点A、B、C.
(2)从点的坐标角度,如何理解函数图象的最高点
提示:图象最高点的纵坐标是所有函数值中的最大值,即函数的最大值.
一
二
(3)如图③所示,图象上最高点C的坐标为(x0,f(x0)),在图象上任取一点A(x,f(x)),f(x)与f(x0)有什么关系
提示:点C是图象的最高点,即对定义域内任意x,均有f(x)≤f(x0)成立.
(4)一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:①对 x∈I,都有f(x)≤M;
② x0∈I,使得f(x0)=M,那么我们就称M是函数y=f(x)的最大值.
其几何意义:函数y=f(x)的最大值是图象最高点的纵坐标.
(5)类比函数最大值的定义,请你给出最小值的定义及其几何意义.
提示:一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
① x∈I,都有f(x)≥M;
② x0∈I,使得f(x0)=M.那么,称M是函数y=f(x)的最小值.
函数最小值的几何意义:函数图象上最低点的纵坐标.
一
二
(6)是否每个函数都有最大值、最小值 如果有最值,取最值的点有几个 举例说明.
提示:一个函数不一定有最值,例如y= 在定义域内没有最大值也没有最小值.有的函数可能只有一个最大(或小)值,例如y=-2x+1,x∈[-1,+∞).如果一个函数存在最值,那么函数的最大值和最小值都是唯一的,但取最值时的自变量可以有多个,如y=x2,x∈[-2,2],最大值只有一个为4,而取最大值的x有x=±2两个.
一
二
2.做一做
已知函数f(x)在[-2,2]上的图象如图所示,则该函数的最小值、最大值分别是( )
A.f(-2),0 B.0,2
C.f(-2),2 D.f(2),2
解析:由题图可知,该函数的最小值为f(-2),最大值为f(1)=2.
答案:C
一
二
二、函数的单调性与最大(小)值
1.(1)若函数y=f(x)在区间[a,b]上是增函数或减函数,它一定有最值吗 如果有,最值是什么
提示:若函数y=f(x)在区间[a,b]上是增函数,则函数的最小值为ymin=f(a),最大值为ymax=f(b);若函数y=f(x)在区间[a,b]上是减函数,则函数的最小值为ymin=f(b),最大值为ymax=f(a).
(2)若函数y=f(x)在区间(a,b)上是增(或减)函数,这个函数有最值吗
活动方案:启发学生画一个符合条件的函数草图,注意端点不在区间内,然后回答.
提示:不存在最值,但可以说函数y=f(x)在区间(a,b)上的值域为(f(a),f(b))[或(f(b),f(a))].
一
二
(3)已知函数y=f(x)的定义域是[a,b],a
2.做一做
函数y=x2-4x+1在[-2,0]上的最大值是 ,最小值是 .
解析:函数y=x2-4x+1在[-2,0]上单调递减,故当x=2时,ymax=13,当x=0时,ymin=1.
答案:13 1
探究一
探究二
探究三
思想方法
随堂演练
利用函数的图象求函数的最值
例1 已知函数y=-|x-1|+2,画出函数的图象,确定函数的最值情况,并写出值域.
分析:去绝对值→分段函数→作图→识图→结论.
由图象知,函数y=-|x-1|+2的最大值为2,没有最小值.所以其值域为(-∞,2].
探究一
探究二
探究三
思想方法
随堂演练
反思感悟
探究一
探究二
探究三
思想方法
随堂演练
(1)画出f(x)的图象;
(2)利用图象写出该函数的最大值和最小值.
解:(1)函数f(x)的图象如图所示.
(2)由图象可知f(x)的最小值为f(1)=1,无最大值.
探究一
探究二
探究三
思想方法
随堂演练
利用函数的单调性求最值
例2 已知函数f(x)=x+ .
(1)判断f(x)在区间[1,2]上的单调性;
(2)根据f(x)的单调性求出f(x)在区间[1,2]上的最值.
分析:(1)证明单调性的流程:取值→作差→变形→判断符号→结论;
(2)借助最值与单调性的关系,写出最值.
探究一
探究二
探究三
思想方法
随堂演练
∵x1
(2)由(1)知f(x)的最小值为f(2),f(2)=2+ =4;f(x)的最大值为f(1).
∵f(1)=1+4=5,∴f(x)的最小值为4,最大值为5.
探究一
探究二
探究三
思想方法
随堂演练
反思感悟 1.利用单调性求函数最值的一般步骤:
(1)判断函数的单调性;(2)利用单调性写出最值.
2.函数的最值与单调性的关系:
(1)若函数f(x)在区间[a,b]上是增(减)函数,则f(x)在区间[a,b]上的最小(大)值是f(a),最大(小)值是f(b).
(2)若函数f(x)在区间[a,b]上是增(减)函数,在区间(b,c]上是减(增)函数,则f(x)在区间[a,c]上的最大(小)值是f(b),最小(大)值是f(a)与f(c)中较小(大)的一个.
(3)若函数f(x)在区间[a,b]上的图象是一条连续不断的曲线,则函数f(x)在区间[a,b]上一定有最值.
(4)求最值时一定要注意所给区间的开闭,若是开区间,则不一定有最大(小)值.
探究一
探究二
探究三
思想方法
随堂演练
延伸探究本例已知条件不变,判断f(x)在区间[1,3]上的单调性,并求f(x)在区间[1,3]上的最值.
当1≤x1
当2
探究二
探究三
思想方法
随堂演练
与最值有关的应用问题
例3 某租赁公司拥有汽车100辆,当每辆车的月租金为3 000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金为3 600元时,能租出多少辆
(2)当每辆车的月租金为多少元时,租赁公司的月收益最大 最大月收益是多少
分析:读题→提取信息→建模→解模→解决实际问题
探究一
探究二
探究三
思想方法
随堂演练
解:(1)当每辆车的月租金为3 600元时,
所以当x=4 050,即每辆车的租金为4 050元时,租赁公司的月收益最大,最大月收益是307 050元.
探究一
探究二
探究三
思想方法
随堂演练
反思感悟 1.本题建立的是二次函数模型,应利用配方法求函数的最值.
2.解函数应用题的一般程序是:
(1)审题.弄清题意,分清条件和结论,理顺数量关系.
(2)建模.将文字语言转化成数学语言,用数学知识建立相应的数学模型.
(3)求模.求解数学模型,得到数学结论.
(4)还原.将用数学方法得到的结论还原为实际问题的意义.
(5)反思回顾.对于数学模型得到的数学解,必须验证这个数学解对实际问题的合理性.
探究一
探究二
探究三
思想方法
随堂演练
变式训练2某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需增加投入100元,已知总收益满足函数:
解:(1)设月产量为x台,则总成本为20 000+100x,
∴当x=300时,f(x)max=25 000,
当x>400时,f(x)=60 000-100x是减函数,
f(x)<60 000-100×400<25 000.∴当x=300时,f(x)max=25 000.
即每月生产300台仪器时利润最大,最大利润为25 000元.
巩固练习
03
探究一
探究二
探究三
思想方法
随堂演练
利用数形结合思想与分类讨论思想求二次函数的最值
典例 求函数y=x2-2ax-1在区间[0,2]上的最值.
【审题视角】可变对称轴x=a→与定区间[0,2]的
相对位置关系→结合单调性与图象求解
解:y=(x-a)2-1-a2.
当a<0时,[0,2]是函数的递增区间,如图①.
故函数在x=0处取得最小值-1,
在x=2处取得最大值3-4a.
当0≤a≤1时,结合函数图象(如图②)知,
函数在x=a处取得最小值-a2-1,
在x=2处取得最大值3-4a.
探究一
探究二
探究三
思想方法
随堂演练
当1
在x=0处取得最大值-1.
当a>2时,[0,2]是函数的递减区间,如图④.
函数在x=0处取得最大值-1,在x=2处取得最小值3-4a.
综上,当a<0时,函数在区间[0,2]上的最小值为-1,最大值为3-4a;
当0≤a≤1时,函数在区间[0,2]上的最小值为-a2-1,最大值为3-4a;
当1
探究一
探究二
探究三
思想方法
随堂演练
方法点睛 1.探求二次函数在给定区间上的最值问题,一般要先作出y=f(x)的草图,再根据图象的增减性进行研究.特别要注意二次函数图象的对称轴与所给区间的位置关系,它是求解二次函数在已知区间上最值问题的主要依据.二次函数图象的对称轴与所给区间的位置关系通常有三种:(1)对称轴在所给区间的右侧;(2)对称轴在所给区间的左侧;(3)对称轴在所给区间内.
探究一
探究二
探究三
思想方法
随堂演练
2.对于二次函数f(x)=a(x-h)2+k(a>0)在区间[m,n]上的最值可作如下讨论:
探究一
探究二
探究三
思想方法
随堂演练
变式训练函数f(x)=x2-2x+2(其中x∈[t,t+1],t∈R)的最小值为g(t),求g(t)的表达式.
解:由函数f(x)=x2-2x+2知其图象的开口向上,对称轴为x=1.下面分三种情况讨论:
图①
当t+1≤1,即t≤0时,如图①所示,此时函数f(x)在[t,t+1]上为减函数,∴g(t)=f(t+1)=(t+1)2-2(t+1)+2=t2+1.
探究一
探究二
探究三
思想方法
随堂演练
如图②所示,此时,函数f(x)在[t,1]上为减函数,
在(1,t+1]上为增函数,
∴g(t)=f(1)=1.
当t≥1时,如图③所示,此时,函数f(x)在[t,t+1]上为增函数,
∴g(t)=f(t)=t2-2t+2.
拓展延伸
04
探究一
探究二
探究三
思想方法
随堂演练
答案:A
2.函数y=|x+1|+2的最小值是( )
A.0 B.-1 C.2 D.3
解析:y=|x+1|+2的图象如图所示.
由图可知函数的最小值为2.
答案:C
探究一
探究二
探究三
思想方法
随堂演练
3.函数y=x2-2x,x∈[0,3]的值域为( )
A.[0,3] B.[-1,0]
C.[-1,+∞) D.[-1,3]
解析:∵函数y=x2-2x=(x-1)2-1,x∈[0,3],∴当x=1时,函数y取得最小值为-1,当x=3时,函数取得最大值为3,故函数的值域为[-1,3],故选D.
答案:D
解析:当x∈[1,2]时,f(x)为增函数,其最大值为f(2)=10;当x∈[-4,1]时,f(x)为减函数,其最大值为f(-4)=11.故函数f(x)的最大值为11.
答案:11
探究一
探究二
探究三
思想方法
随堂演练
5.把长为12 cm的细铁丝截成两段,各自围成一个正方形,求这两个正方形面积之和的最小值.
人教高中A版必修一数学课件
第2课时 函数的最大(小)值
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
