人教版六年级数学上册第七单元扇形统计图(知识点梳理+能力百分练)四(含答案)
文档属性
| 名称 | 人教版六年级数学上册第七单元扇形统计图(知识点梳理+能力百分练)四(含答案) |  | |
| 格式 | docx | ||
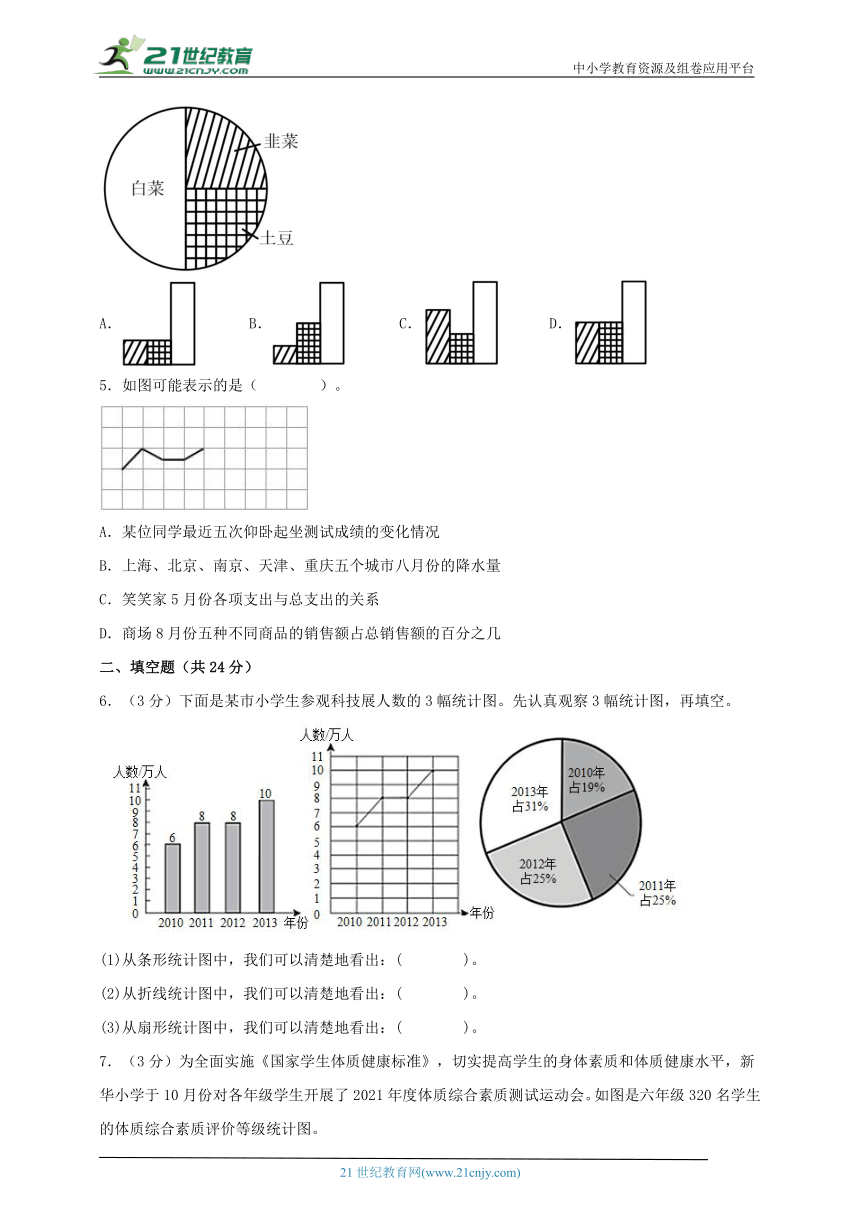
| 文件大小 | 743.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 14:55:59 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版六年级数学上册第七单元扇形统计图(知识点梳理+能力百分练)四
知识点梳理
1、扇形统计图的意义:用整个圆的面积表示总数,用圆内各个扇形面积表示各部分数量同总数之间的关系,也就是各部分数量占总数的百分比。
2、常用统计图的优点:条形统计图;可以清楚的看出各种数量的多少;折线统计图:不仅可以看出各种数量的多少,还可以清晰看出数量的增减变化情况;扇形统计图;能够清楚的反映出各部分数量同总数之间的关系。
能力百分练
一、选择题(共10分)
1.妈妈想清楚地表示家里每月收入与各项消费的支出、储蓄理财等之间的关系,应该选用( )统计图比较好。
A.扇形 B.折线 C.条形 D.以上三种统计图任选一个
2.601班有40名学生在投票选举班长活动中,得票情况如下:小何20票,小赵10票,小邓6票,小李4票。下面图( )最能反映每人得票情况所占百分比。
A. B. C. D.
3.六(2)班有40名学生,选举优秀班干部的得票数为:小红20票,小明10票,小兰6票,小华4票。下列四幅图中,能正确地表示这一结果的是( )。
A. B.
C. D.
4.爷爷在菜园里种了三种菜(如图),用条形统计图表示各种菜占地面积的关系,应该是图( )。
A. B. C. D.
5.如图可能表示的是( )。
A.某位同学最近五次仰卧起坐测试成绩的变化情况
B.上海、北京、南京、天津、重庆五个城市八月份的降水量
C.笑笑家5月份各项支出与总支出的关系
D.商场8月份五种不同商品的销售额占总销售额的百分之几
二、填空题(共24分)
6.(3分)下面是某市小学生参观科技展人数的3幅统计图。先认真观察3幅统计图,再填空。
(1)从条形统计图中,我们可以清楚地看出:( )。
(2)从折线统计图中,我们可以清楚地看出:( )。
(3)从扇形统计图中,我们可以清楚地看出:( )。
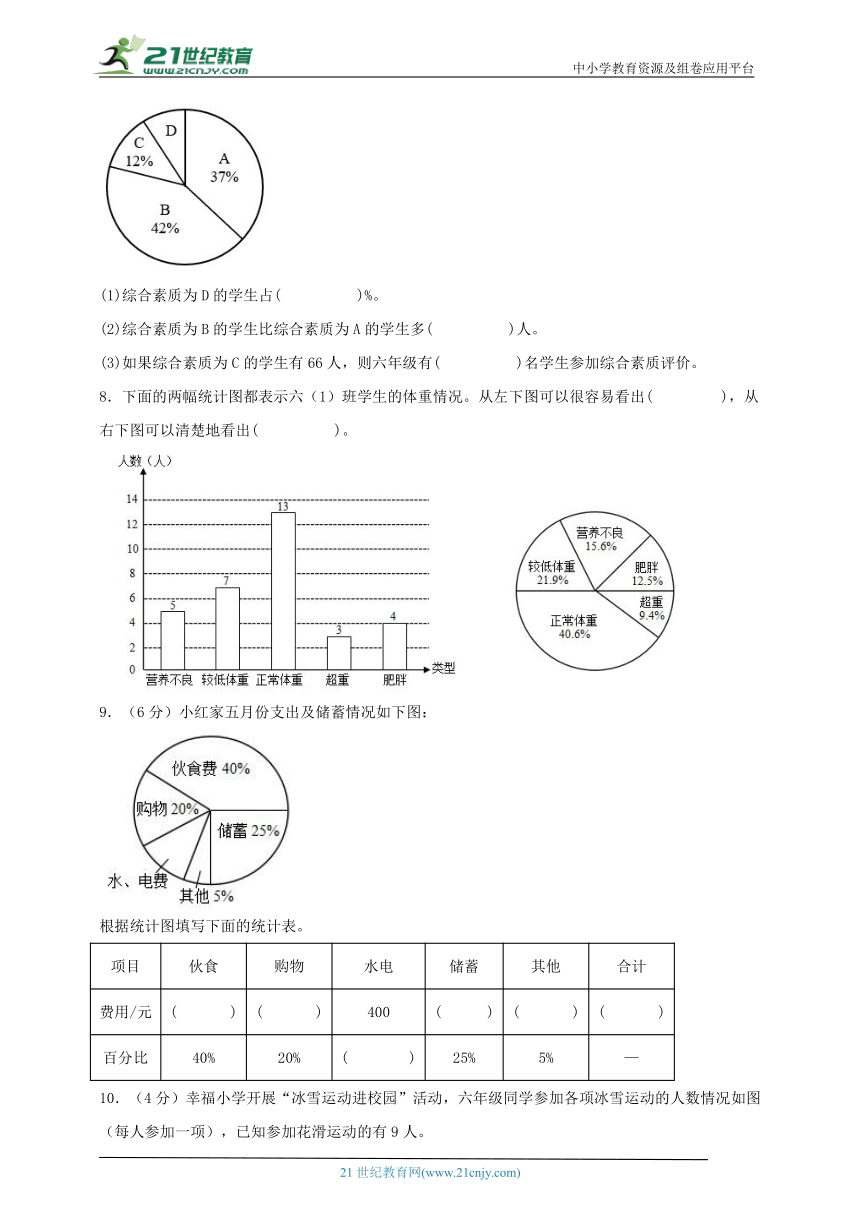
7.(3分)为全面实施《国家学生体质健康标准》,切实提高学生的身体素质和体质健康水平,新华小学于10月份对各年级学生开展了2021年度体质综合素质测试运动会。如图是六年级320名学生的体质综合素质评价等级统计图。
(1)综合素质为D的学生占( )%。
(2)综合素质为B的学生比综合素质为A的学生多( )人。
(3)如果综合素质为C的学生有66人,则六年级有( )名学生参加综合素质评价。
8.下面的两幅统计图都表示六(1)班学生的体重情况。从左下图可以很容易看出( ),从右下图可以清楚地看出( )。
9.(6分)小红家五月份支出及储蓄情况如下图:
根据统计图填写下面的统计表。
项目 伙食 购物 水电 储蓄 其他 合计
费用/元 ( ) ( ) 400 ( ) ( ) ( )
百分比 40% 20% ( ) 25% 5% —
10.(4分)幸福小学开展“冰雪运动进校园”活动,六年级同学参加各项冰雪运动的人数情况如图(每人参加一项),已知参加花滑运动的有9人。
(1)六年级共有( )人参加了冰雪运动。
(2)参加( )运动的人数最多,有( )人。
(3)参加旱地冰壶运动的人数比参加雪地足球运动的少( )%。
11.(6分)下图是六(2)班学生喜欢球类运动的扇形统计图。
(1)六(2)班喜欢球类的人数占全班总人数的百分比之和应该是( )%。
(2)喜欢( )球的人数最多,占全班人数的( )%。
(3)若六(2)班有40人,则喜欢足球的有( )人,喜欢篮球的有( )人。
(4)若喜欢羽毛球的有12人,那么六(2)班一共有( )人。
三、判断题(共8分)
12.小明记录分析自己各单元数学测试成绩的波动情况,用条形统计图比较合适。( )
13.某小学学生用手机查资料的人数占69.4%,玩游戏的占51.2%,这些统计数据可以用扇形统计图表示。( )
14.要反映某地区2022年全年降水量的变化情况,应绘制折线统计图。( )
15.条形统计图能清楚的表示出数量的多少,折线统计图更容易看出数量增减变化的情况,扇形统计图可以看出各部分与整体的关系。( )
四、作图题(共6分)
16.(6分)为响应“光盘行动”,让同学们珍惜粮食。某校在某日午餐后,随机抽查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制了如下所示的不完整统计图,请你根据信息补充完统计图。
五、解答题(共52分)
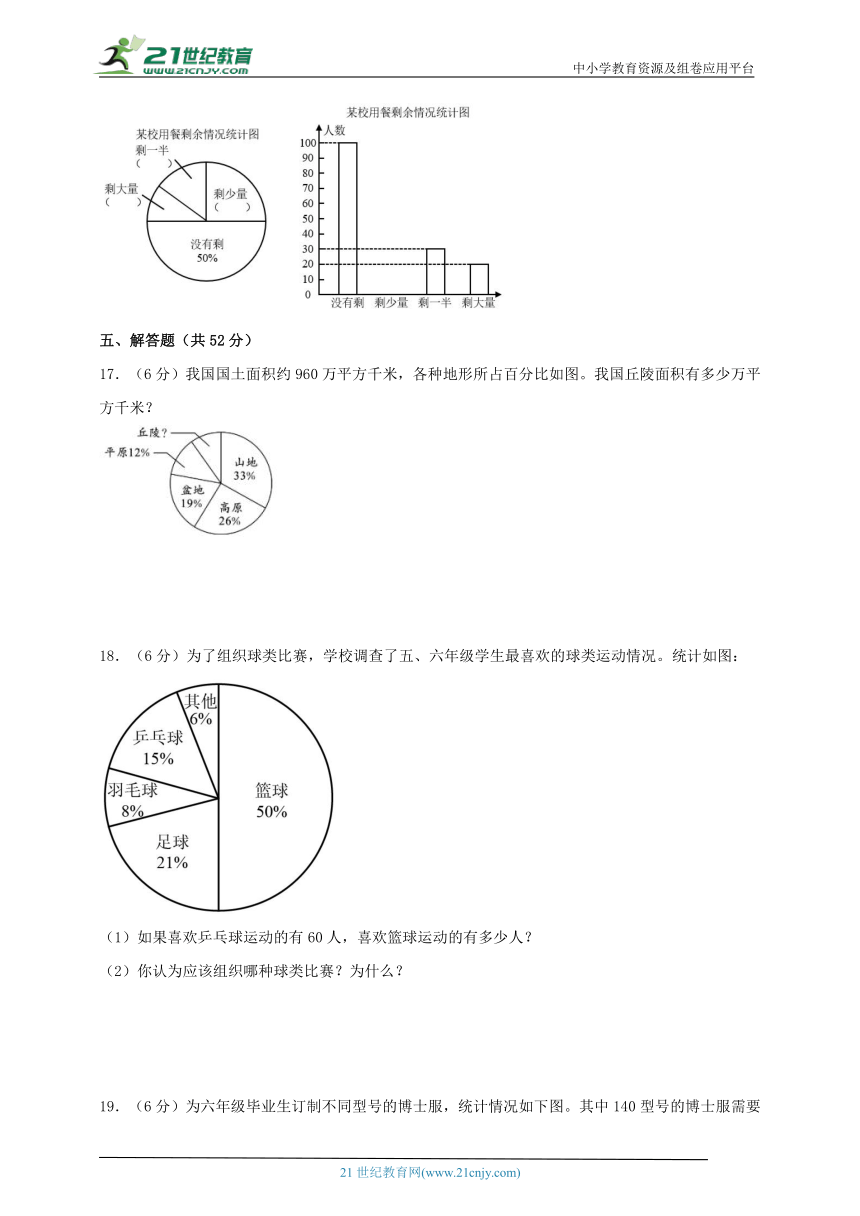
17.(6分)我国国土面积约960万平方千米,各种地形所占百分比如图。我国丘陵面积有多少万平方千米?
18.(6分)为了组织球类比赛,学校调查了五、六年级学生最喜欢的球类运动情况。统计如图:
(1)如果喜欢乒乓球运动的有60人,喜欢篮球运动的有多少人?
(2)你认为应该组织哪种球类比赛?为什么?
19.(6分)为六年级毕业生订制不同型号的博士服,统计情况如下图。其中140型号的博士服需要做64件,那么150型号的博士服需要做多少件?
20.(12分)根据统计表完成下面各题,下面是六年级一班半期检测成绩统计表。
六年级一班半期检测成绩统计表
分数 90分及以上 80—90分以下 60—80分以下 60分以下
人数 10人 10人 5人
(1)80—90分以下的占全班人数的50%,请根据这一信息,完成统计表。
(2)六年级一班的优生率是多少?(提示:90分及以上为优生)
(3)六年级一班的不合格率是多少?(提示:60分以下为不合格)
(4)请把扇形统计图补充完整。
21.(11分)近年来,北京市把保护环境提到了新的高度,大力倡导绿色出行。聪聪调查了某学校教师的出行方式情况,并制成了两幅统计图。
(1)一共调查了( )名教师。
(2)坐公交的有( )人。
(3)开车的占( )%。
(4)将条形统计图和扇形统计图补充完整。
(5)你认为这所学校的教师在“绿色出行”方面做得怎么样?写出你的理由。
22.(11分)如今,很多人都是“手机不离手”。疫情发生以来,有的人手机使用时间比以前更长了,也有人养成了健康、有节律的手机使用习惯。近日,中国青年报社对中学生、大学生和上班族进行了一项抽样调查,记者把调查结果绘制成如下的统计图(如下图)。
(1)结合两幅统计图中的数据,可以算出接受调查的一共有( )人。
(2)每天使用手机5小时以上的占全部受调查人数的( )%,有( )人,请在统计图(2)上补充完整。
(3)88.5%的受调查者坦言最近手机使用时长增加了,主要用手机刷短视频、上网课和沟通工作。由于长时间观看手机屏幕会使眼睛疲劳、干涩,引发视力下降,所以,养成健康、自律的手机使用意识和习惯很重要。对此,你有什么好的建议?(至少写出两条)
参考答案
1.A
【分析】条形统计图可以清楚地看出数量的多少;
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况;
扇形统计图表示各部分数量与总数之间的关系。
【详解】妈妈想清楚地表示家里每月收入与各项消费的支出、储蓄理财等之间的关系,应该选用扇形统计图比较好。
故答案为:A
【点睛】理解掌握条形统计图、折线统计图、扇形统计图的特点是选择统计图的关键。
2.C
【分析】先求出4人所占的百分比,再分别乘上360°求出所对应的度数,最后和各选项做对比即可,包含四个度数的选项就是正确选项。
【详解】小何:20÷40×100%=50%,50%×360°=180°。
小赵:10÷40×100%=25%,25%×360°=90°。
小邓:6÷40×100%=15%,15%×360°=54°。
小李:4÷40×100%=10%,10%×360°=36°。
故答案为:C
【点睛】此题考查扇形统计图的应用,求出百分比所对应的度数是解题的关键。
3.A
【分析】先用加法求出总票数是40票,把总票数看作单位“1”,根据“求一个数占另一个数的百分之几”,用除法求出小红、小明、以及小兰与小华的票数之和分别占总票数的百分比,再通过分析比较,确定哪幅图能正确地表示这一结果。
【详解】总票数:20+10+6+4=40(票)
小红占:
20÷40×100%
=0.5×100%
=50%
小明占:
10÷40×100%
=0.25×100%
=25%
小兰和小华共占:
(6+4)÷40×100%
=10÷40×100%
=0.25×100%
=25%
综上所述,小红占50%,小明占25%,小兰和小华共占25%,且小兰的占比稍大于小华的占比;
A.每个人的占比都正确地表示出来了,符合题意;
B.没有表示出小红占50%、小明占25%,不符合题意;
C.没有表示出小明占25%、小兰和小华共占25%,不符合题意;
D.没有表示出每个人的占比,不符合题意。
故答案为:A
【点睛】扇形统计图清楚地看出各部分数量与总数量之间的关系,先求出每人的票数占总票数的百分之几,再选择正确的扇形统计图。
4.D
【分析】扇形统计图中用整个圆表示总数量,圆内各个扇形的大小表示各部分数量占总数量的百分比,观察扇形统计图可知,白菜的种植面积最大,占菜地总面积的50%,韭菜和土豆的种植面积相等,各占菜地总面积的25%,韭菜或土豆的种植面积占白菜种植面积的一半,据此解答。
【详解】A.韭菜或土豆的种植面积不到白菜种植面积的一半;
B.韭菜和土豆的种植面积不相等;
C.韭菜和土豆的种植面积不相等;
D.韭菜和土豆的种植面积相等,且占白菜种植面积的一半。
故答案为:D
【点睛】理解并掌握扇形统计图的特点及作用是解答题目的关键。
5.A
【分析】条形统计图特点是用一个单位长度表示一定的数量,用直条的长短表示数量的多少,作用是从图中能清楚地看出各种数量的多少,便于相互比较。
折线统计图特点是用不同位置的点表示数量的多少,根据数量的多少描出各点,然后把各点用线段顺次连接起来。不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
扇形统计图特点是以一个圆的面积表示物体的总数量,以相应的扇形面积占整个圆面积的百分数表示各有关部分占总数量的百分数。清楚地看出各部分数量与总数量之间的关系。
【详解】A.某位同学最近五次仰卧起坐测试成绩的变化情况,有可能;
B.上海、北京、南京、天津、重庆五个城市八月份的降水量适合用条形统计图,排除;
C.笑笑家5月份各项支出与总支出的关系,适合用扇形统计图,排除;
D.商场8月份五种不同商品的销售额占总销售额的百分之几,适合用扇形统计图,排除。
故答案为:A
【点睛】关键是熟悉各种统计图的特点,根据统计图的特点进行分析。
6.(1)2010年至2013年每一年的具体人数情况
(2)2010年至2013年每一年的人数变化情况
(3)2010年至2013年每一年的人数占这4年总的人数的百分比情况
【分析】条形统计图可以看出数据情况,折线统计图可以反映数据的变化情况,扇形统计图可以反映各个部分数量和总量之间的关系。据此,再结合题中数据的具体情景,分析填空即可。
【详解】(1)从条形统计图中,我们可以清楚地看出:2010年至2013年每一年的具体人数情况。
(2)从折线统计图中,我们可以清楚地看出:2010年至2013年每一年的人数变化情况。
(3)从扇形统计图中,我们可以清楚地看出:2010年至2013年每一年的人数占这4年总的人数的百分比情况。
【点睛】掌握条形统计图、折线统计图以及扇形统计图的特点是解题的关键。
7.(1)9
(2)16
(3)550
【分析】(1)将六年级参加综合素质评价的全体学生人数看作单位“1”,用总体减去综合素质为A、B和C的学生所占的百分数,所得结果即为综合素质为D的学生占的百分数;
(2)用减法计算综合素质为B的学生和综合素质为A的学生的所占的百分数之差,再根据求一个数的百分之几是多少,用乘法计算;
(3)将六年级参加综合素质评价的学生看作单位“1”,其中综合素质为C的学生占12%,也就是66人,要求全体学生人数,用除法计算。
【详解】(1)1-(37%+42%+12%)
=1-91%
=9%
所以综合素质为D的学生占9%。
(2)320×(42%-37%)
=320×5%
=16(人)
所以综合素质为B的学生比综合素质为A的学生多16人。
(3)66÷12%=550(名)
所以如果综合素质为C的学生有66人,那么六年级有550名学生参加综合素质评价。
【点睛】解答本题的关键是理解掌握扇形统计图的特点,并且能够根据统计图提供的信息,解决相关问题。
8. 六(1)班各种类型体重的具体学生人数 六(1)班各种类型体重的人数占总人数的百分比
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】面的两幅统计图都表示六(1)班学生的体重情况。从左下图可以很容易看出六(1)班各种类型体重的具体学生人数,从右下图可以清楚地看出六(1)班各种类型体重的人数占总人数的百分比。例如:六(1)班营养不良的有5人,占六(1)班学生人数的15.6%。
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
9. 1600 800 1000 200 4000 10%
【分析】根据扇形统计图求出水电费用所占的百分比,用水电费用400元除以其对应分率,即可求出小红家五月份支出及储蓄总额,进一步求出各项费用即可。
【详解】水电费用所占的百分比:
1-40%-20%-25%-5%=10%
合计:400÷10%=4000(元)
伙食费用:4000×40%=1600(元)
购物费用:4000×20%=800(元)
储蓄:4000×25%=1000(元)
其他:4000×5%=200(元)
【点睛】本题考查扇形统计图的综合应用。已知一个数的几(百)分之几是多少,求这个数,用除法计算;求一个数的百分之几是多少,用乘法计算。
10.(1)60
(2) 轮滑 24
(3)20
【分析】(1)把六年级同学参加运动的总人数看作单位“1”,根据减法的意义,用1-20%-25%-40%即可求出参加花滑运动人数占总人数的百分比;已知参加花滑运动的有9人,根据百分数除法的意义,用9÷(1-20%-25%-40%)即可求出总人数;
(2)比较每项运动占的百分比,发现参加轮滑运动的人数最多,根据百分数乘法的意义,用总人数乘40%即可求出参加轮滑运动的人数;
(3)根据求一个数比另一个数少百分之几,用相差数除以另一个数再乘100%,则用(25%-20%)÷25%×100%即可求出参加旱地冰壶运动的人数比参加雪地足球运动的少百分之几。
【详解】(1)1-20%-25%-40%=15%
9÷15%=60(人)
六年级共有60人参加了冰雪运动。
(2)15%<20%<25%<40%
参加轮滑运动的人数最多,有24人。
(3)(25%-20%)÷25%×100%
=5%÷25%×100%
=20%
参加旱地冰壶运动的人数比参加雪地足球运动的少20%。
【点睛】此题考査的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
11.(1)100
(2) 乒乓 50
(3) 2 10
(4)60
【分析】(1)把全班学生人数看作单位“1”,六(2)班喜欢球类的人数占全班总人数的百分比之和应该是100%。
(2)通过观察统计图可知,比较喜欢乒乓球、篮球、足球、羽毛球占全班总人数的百分比的大小,即可求出喜欢乒乓球的人数最多,占全班人数的50%。
(3)根据求一个数的百分之几是多少,用乘法解决,用总人数分别乘喜欢足球、喜欢篮球的人数占总人数的百分比,即可求出喜欢足球和喜欢篮球的人数各是多少。
(4)把全班学生人数看作单位“1”,喜欢羽毛球的有12人,占全班人数的20%,已知一个数的百分之几是多少,求这个数,用除法解答。
【详解】(1)50%+25%+5%+20%=100%
六(2)班喜欢球类的人数占全班总人数的百分比之和应该是100%。
(2)5%<20%<25%<50%
喜欢乒乓球的人数最多,占全班人数的50%。
(3)40×5%=2(人)
40×25%=10(人)
喜欢足球的有2人,喜欢篮球的有10人。
(4)12÷20%=60(人)
六(2)班一共有60人。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
12.×
【分析】条形统计图用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;扇形统计图中用整个圆表示总数量,圆内各个扇形的大小表示各部分数量占总数量的百分比,通过扇形统计图可以清楚地看出各部分数量与总数量之间,部分数量与部分数量之间的关系,据此解答。
【详解】分析可知,小明记录分析自己各单元数学测试成绩的波动情况,用折线统计图比较合适。
故答案为:×
【点睛】本题主要考查统计图的选择,掌握各统计图的特点及作用是解答题目的关键。
13.×
【分析】扇形统计图中用整个圆表示总数量,圆内各个扇形的大小表示各部分数量占总数量的百分比,通过扇形统计图可以清楚地看出各部分数量与总数量之间,各项的百分比之和不能超过100%,据此解答。
【详解】69.4%+51.2%=120.6%
因为120.6%>100%,也就是说被调查的学生中,有同时选择两项或两项以上的,所以不能用扇形统计图表示某小学学生用手机查资料的人数和玩游戏的人数占总人数的百分率。
故答案为:×
【点睛】掌握扇形统计图的特点及作用是解答题目的关键。
14.√
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】根据分析可知,要反映某地区2022年全年降水量的变化情况,应绘制折线统计图。原题干说法正确。
故答案为:√
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
15.√
【分析】根据条形统计图、折线统计图、扇形统计图的特征分析题中说法是否正确即可。
【详解】条形统计图:用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;
折线统计图:不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;
扇形统计图:扇形统计图可以清楚地看出各部分数量与总数量之间,部分数量与部分数量之间的关系;
由上可知,题中说法正确。
故答案为:√
【点睛】理解并掌握各统计图的特征是解答题目的关键。
16.见详解
【分析】将总人数看作单位“1”,没有剩的人数÷对应百分率=总人数,总人数-剩一半的人数-剩大量的人数=剩少量的人数,据此补充条形统计图;分别用剩少量、剩一半、剩大量的人数除以总人数,求出剩少量、剩一半、剩大量的对应百分率,补充扇形统计图即可。
【详解】100÷50%=200(人)
200-100-30-20=50(人)
50÷200=0.25=25%
30÷200=0.15=15%
20÷200=0.1=10%
如图所示:
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数相关解题思路解答即可。
17.96万平方千米
【分析】把我国国土面积看作单位“1”,用单位“1”减去山地、高原、盆地、平原占国土面积的百分率,即可求出丘陵占国土的百分率,再根据求一个数的百分之几是多少,用乘法计算即可。
【详解】960×(1-33%-26%-19%-12%)
=960×10%
=96(万平方千米)
答:我国丘陵面积有96万平方千米。
【点睛】本题考查求一个数的百分之几是多少,明确用乘法是解题的关键。
18.(1)200人
(2)篮球比赛,理由见详解
【分析】(1)由题意可知,喜欢乒乓球的人数占总人数的15%,有60人,根据已知一个数的百分之几是多少,求这个数,用除法计算,用60除以15%求出总人数,再根据求一个数的百分之几是多少,用乘法计算,用总人数乘50%即可求出喜欢篮球运动的有多少人;
(2)通过扇形统计图可知,喜欢篮球的人数多,则应该组织篮球比赛。
【详解】(1)60÷15%×50%
=400×50%
=200(人)
答:喜欢篮球运动的有200人。
(2)应该组织篮球比赛,因为喜欢篮球的人数多。
【点睛】本题考查已知一个数的百分之几是多少,求这个数,明确用除法是解题的关键。
19.224件
【分析】140型号的博士服的数量占六年级毕业生博士服总套数的8%,其中140型号的博士服需要做64件,已知一个数的百分之几是多少,求这个数,用除法,用64除以8%,求出博士服的总数量,再乘150型号的博士服数量占总数量的28%,即可求出150型号的博士服需要做多少件。
【详解】64÷8%×28%
=64÷0.08×0.28
=800×0.28
=224(件)
答:150型号的博士服需要做224件。
【点睛】此题的解题关键是理解扇形统计图的特点,掌握求一个数的百分之几是多少和已知一个数的百分之几是多少,求这个数的计算方法。
20.(1)25人;
(2)20%;
(3)10%;
(4)见详解
【分析】(1)把六年级一班的总人数看作单位“1”,80—90分以下的占全班人数的50%,则90分及以上、60—80分以下、60分以下一共占总人数的(1-50%),根据量÷对应的百分率=单位“1”求出六年级一班的总人数,80—90分以下的人数=总人数×50%;
(2)六年级一班的优生率=90分及以上的人数÷六年级一班的总人数×100%;
(3)六年级一班的不合格率=60分以下的人数÷六年级一班的总人数×100%;
(4)扇形统计图中用整个圆表示总数量,圆内各个扇形的大小表示各部分数量占总数量的百分比,90分及以上的人数占总人数的20%,80—90分以下的人数占总人数的50%,60—80分以下的人数与90分及以上的人数相同,都占总人数的20%,60分以下的人数占总人数的10%,据此解答。
【详解】(1)(10+10+5)÷(1-50%)
=25÷0.5
=50(人)
50×50%=25(人)
所以,80—90分以下的有25人。
分数 90分及以上 80—90分以下 60—80分以下 60分以下
人数 10人 25人 10人 5人
(2)10÷50×100%
=0.2×100%
=20%
答:六年级一班的优生率是20%。
(3)5÷50×100%
=0.1×100%
=10%
答:六年级一班的不合格率是10%。
(4)分析可知:
【点睛】根据量和对应的百分率求出总人数,并掌握一个数占另一个数百分之几的计算方法以及扇形统计图的特点和作用是解答题目的关键。
21.(1)200
(2)60
(3)10
(4)见详解
(5)见详解
【分析】(1)结合两幅统计图可知,步行的教师有36人占调查总人数的18%,把调查的总人数看作单位“1”,根据已知一个数的百分之几是多少,求这个数,用除法计算,即可求出总人数。
(2)把调查的总人数看作单位“1”,已知坐公交车的教师人数占总人数的30%,根据求一个数的百分之几是多少,用乘法计算,即可求出坐公交车的教师人数。
(3)用开车的教师人数除以总人数,即可求出开车的人数占总人数百分之几。
(4)根据第(2)(3)题的数据,将条形统计图和扇形统计图补充完整。
(5)结合两幅统计图中的信息,写出自己的见解,合理即可。
【详解】(1)36÷18%
=36÷0.18
=200(名)
一共调查了200名教师。
(2)200×30%
=200×0.3
=60(人)
坐公交的有60人。
(3)20÷200×100%
=0.1×100%
=10%
开车的占10%。
(4)如图:
(5)我认为这所学校的教师在“绿色出行”方面做得好,大部分教师都选择了绿色出行方式。(答案不唯一)
【点睛】本题考查统计图的综合应用,掌握条形统计图、扇形统计图的特点及作用,从统计图中获取信息,并根据获取的信息解决有关的实际问题。
22.(1)2000
(2)45;900;见详解
(3)见详解
【分析】(1)从两幅统计图中可知,每天使用手机1~3小时的有360人,占全部接受调查人数的18%,把接受调查的总人数看作单位“1”,根据已知一个数的百分之几是多少,求这个数,用除法计算,即可求出接受调查的总人数。
(2)先用每天使用手机1小时以内的40人除以接受调查的总人数,求出每天使用手机1小时以内的人数占总人数的百分比。
把接受调查的总人数看作单位“1”,根据减法的意义,用“1”分别减去已知的每天使用手机的各时间段人数占总人数的百分比,即是每天使用手机5小时以上的占全部接受调查人数的百分比。
根据求一个数的百分之几是多少,用总人数乘每天使用手机5小时以上的百分比,即可求出每天使用手机5小时以上的人数。
据此将条形统计图补充完整。
(3)结合统计图中的信息,提出建议,合理即可。
【详解】(1)360÷18%
=360÷0.18
=2000(人)
接受调查的一共有2000人。
(2)40÷2000×100%
=0.02×100%
=2%
1-2%-18%-35%=45%
2000×45%
=2000×0.45
=900(人)
每天使用手机5小时以上的占全部受调查人数的45%,有900人。
如图:
(3)我建议:①合理安排好手机使用时间,做到上网生活两不误。②平时多参加体育锻炼和课外活动,每天有计划地看看绿色植物,放松眼睛。(答案不唯一)
【点睛】本题考查统计图的综合应用,掌握条形统计图和扇形统计图的特点和作用,从统计图中获取信息,根据获取的信息解决有关的实际问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版六年级数学上册第七单元扇形统计图(知识点梳理+能力百分练)四
知识点梳理
1、扇形统计图的意义:用整个圆的面积表示总数,用圆内各个扇形面积表示各部分数量同总数之间的关系,也就是各部分数量占总数的百分比。
2、常用统计图的优点:条形统计图;可以清楚的看出各种数量的多少;折线统计图:不仅可以看出各种数量的多少,还可以清晰看出数量的增减变化情况;扇形统计图;能够清楚的反映出各部分数量同总数之间的关系。
能力百分练
一、选择题(共10分)
1.妈妈想清楚地表示家里每月收入与各项消费的支出、储蓄理财等之间的关系,应该选用( )统计图比较好。
A.扇形 B.折线 C.条形 D.以上三种统计图任选一个
2.601班有40名学生在投票选举班长活动中,得票情况如下:小何20票,小赵10票,小邓6票,小李4票。下面图( )最能反映每人得票情况所占百分比。
A. B. C. D.
3.六(2)班有40名学生,选举优秀班干部的得票数为:小红20票,小明10票,小兰6票,小华4票。下列四幅图中,能正确地表示这一结果的是( )。
A. B.
C. D.
4.爷爷在菜园里种了三种菜(如图),用条形统计图表示各种菜占地面积的关系,应该是图( )。
A. B. C. D.
5.如图可能表示的是( )。
A.某位同学最近五次仰卧起坐测试成绩的变化情况
B.上海、北京、南京、天津、重庆五个城市八月份的降水量
C.笑笑家5月份各项支出与总支出的关系
D.商场8月份五种不同商品的销售额占总销售额的百分之几
二、填空题(共24分)
6.(3分)下面是某市小学生参观科技展人数的3幅统计图。先认真观察3幅统计图,再填空。
(1)从条形统计图中,我们可以清楚地看出:( )。
(2)从折线统计图中,我们可以清楚地看出:( )。
(3)从扇形统计图中,我们可以清楚地看出:( )。
7.(3分)为全面实施《国家学生体质健康标准》,切实提高学生的身体素质和体质健康水平,新华小学于10月份对各年级学生开展了2021年度体质综合素质测试运动会。如图是六年级320名学生的体质综合素质评价等级统计图。
(1)综合素质为D的学生占( )%。
(2)综合素质为B的学生比综合素质为A的学生多( )人。
(3)如果综合素质为C的学生有66人,则六年级有( )名学生参加综合素质评价。
8.下面的两幅统计图都表示六(1)班学生的体重情况。从左下图可以很容易看出( ),从右下图可以清楚地看出( )。
9.(6分)小红家五月份支出及储蓄情况如下图:
根据统计图填写下面的统计表。
项目 伙食 购物 水电 储蓄 其他 合计
费用/元 ( ) ( ) 400 ( ) ( ) ( )
百分比 40% 20% ( ) 25% 5% —
10.(4分)幸福小学开展“冰雪运动进校园”活动,六年级同学参加各项冰雪运动的人数情况如图(每人参加一项),已知参加花滑运动的有9人。
(1)六年级共有( )人参加了冰雪运动。
(2)参加( )运动的人数最多,有( )人。
(3)参加旱地冰壶运动的人数比参加雪地足球运动的少( )%。
11.(6分)下图是六(2)班学生喜欢球类运动的扇形统计图。
(1)六(2)班喜欢球类的人数占全班总人数的百分比之和应该是( )%。
(2)喜欢( )球的人数最多,占全班人数的( )%。
(3)若六(2)班有40人,则喜欢足球的有( )人,喜欢篮球的有( )人。
(4)若喜欢羽毛球的有12人,那么六(2)班一共有( )人。
三、判断题(共8分)
12.小明记录分析自己各单元数学测试成绩的波动情况,用条形统计图比较合适。( )
13.某小学学生用手机查资料的人数占69.4%,玩游戏的占51.2%,这些统计数据可以用扇形统计图表示。( )
14.要反映某地区2022年全年降水量的变化情况,应绘制折线统计图。( )
15.条形统计图能清楚的表示出数量的多少,折线统计图更容易看出数量增减变化的情况,扇形统计图可以看出各部分与整体的关系。( )
四、作图题(共6分)
16.(6分)为响应“光盘行动”,让同学们珍惜粮食。某校在某日午餐后,随机抽查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制了如下所示的不完整统计图,请你根据信息补充完统计图。
五、解答题(共52分)
17.(6分)我国国土面积约960万平方千米,各种地形所占百分比如图。我国丘陵面积有多少万平方千米?
18.(6分)为了组织球类比赛,学校调查了五、六年级学生最喜欢的球类运动情况。统计如图:
(1)如果喜欢乒乓球运动的有60人,喜欢篮球运动的有多少人?
(2)你认为应该组织哪种球类比赛?为什么?
19.(6分)为六年级毕业生订制不同型号的博士服,统计情况如下图。其中140型号的博士服需要做64件,那么150型号的博士服需要做多少件?
20.(12分)根据统计表完成下面各题,下面是六年级一班半期检测成绩统计表。
六年级一班半期检测成绩统计表
分数 90分及以上 80—90分以下 60—80分以下 60分以下
人数 10人 10人 5人
(1)80—90分以下的占全班人数的50%,请根据这一信息,完成统计表。
(2)六年级一班的优生率是多少?(提示:90分及以上为优生)
(3)六年级一班的不合格率是多少?(提示:60分以下为不合格)
(4)请把扇形统计图补充完整。
21.(11分)近年来,北京市把保护环境提到了新的高度,大力倡导绿色出行。聪聪调查了某学校教师的出行方式情况,并制成了两幅统计图。
(1)一共调查了( )名教师。
(2)坐公交的有( )人。
(3)开车的占( )%。
(4)将条形统计图和扇形统计图补充完整。
(5)你认为这所学校的教师在“绿色出行”方面做得怎么样?写出你的理由。
22.(11分)如今,很多人都是“手机不离手”。疫情发生以来,有的人手机使用时间比以前更长了,也有人养成了健康、有节律的手机使用习惯。近日,中国青年报社对中学生、大学生和上班族进行了一项抽样调查,记者把调查结果绘制成如下的统计图(如下图)。
(1)结合两幅统计图中的数据,可以算出接受调查的一共有( )人。
(2)每天使用手机5小时以上的占全部受调查人数的( )%,有( )人,请在统计图(2)上补充完整。
(3)88.5%的受调查者坦言最近手机使用时长增加了,主要用手机刷短视频、上网课和沟通工作。由于长时间观看手机屏幕会使眼睛疲劳、干涩,引发视力下降,所以,养成健康、自律的手机使用意识和习惯很重要。对此,你有什么好的建议?(至少写出两条)
参考答案
1.A
【分析】条形统计图可以清楚地看出数量的多少;
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况;
扇形统计图表示各部分数量与总数之间的关系。
【详解】妈妈想清楚地表示家里每月收入与各项消费的支出、储蓄理财等之间的关系,应该选用扇形统计图比较好。
故答案为:A
【点睛】理解掌握条形统计图、折线统计图、扇形统计图的特点是选择统计图的关键。
2.C
【分析】先求出4人所占的百分比,再分别乘上360°求出所对应的度数,最后和各选项做对比即可,包含四个度数的选项就是正确选项。
【详解】小何:20÷40×100%=50%,50%×360°=180°。
小赵:10÷40×100%=25%,25%×360°=90°。
小邓:6÷40×100%=15%,15%×360°=54°。
小李:4÷40×100%=10%,10%×360°=36°。
故答案为:C
【点睛】此题考查扇形统计图的应用,求出百分比所对应的度数是解题的关键。
3.A
【分析】先用加法求出总票数是40票,把总票数看作单位“1”,根据“求一个数占另一个数的百分之几”,用除法求出小红、小明、以及小兰与小华的票数之和分别占总票数的百分比,再通过分析比较,确定哪幅图能正确地表示这一结果。
【详解】总票数:20+10+6+4=40(票)
小红占:
20÷40×100%
=0.5×100%
=50%
小明占:
10÷40×100%
=0.25×100%
=25%
小兰和小华共占:
(6+4)÷40×100%
=10÷40×100%
=0.25×100%
=25%
综上所述,小红占50%,小明占25%,小兰和小华共占25%,且小兰的占比稍大于小华的占比;
A.每个人的占比都正确地表示出来了,符合题意;
B.没有表示出小红占50%、小明占25%,不符合题意;
C.没有表示出小明占25%、小兰和小华共占25%,不符合题意;
D.没有表示出每个人的占比,不符合题意。
故答案为:A
【点睛】扇形统计图清楚地看出各部分数量与总数量之间的关系,先求出每人的票数占总票数的百分之几,再选择正确的扇形统计图。
4.D
【分析】扇形统计图中用整个圆表示总数量,圆内各个扇形的大小表示各部分数量占总数量的百分比,观察扇形统计图可知,白菜的种植面积最大,占菜地总面积的50%,韭菜和土豆的种植面积相等,各占菜地总面积的25%,韭菜或土豆的种植面积占白菜种植面积的一半,据此解答。
【详解】A.韭菜或土豆的种植面积不到白菜种植面积的一半;
B.韭菜和土豆的种植面积不相等;
C.韭菜和土豆的种植面积不相等;
D.韭菜和土豆的种植面积相等,且占白菜种植面积的一半。
故答案为:D
【点睛】理解并掌握扇形统计图的特点及作用是解答题目的关键。
5.A
【分析】条形统计图特点是用一个单位长度表示一定的数量,用直条的长短表示数量的多少,作用是从图中能清楚地看出各种数量的多少,便于相互比较。
折线统计图特点是用不同位置的点表示数量的多少,根据数量的多少描出各点,然后把各点用线段顺次连接起来。不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
扇形统计图特点是以一个圆的面积表示物体的总数量,以相应的扇形面积占整个圆面积的百分数表示各有关部分占总数量的百分数。清楚地看出各部分数量与总数量之间的关系。
【详解】A.某位同学最近五次仰卧起坐测试成绩的变化情况,有可能;
B.上海、北京、南京、天津、重庆五个城市八月份的降水量适合用条形统计图,排除;
C.笑笑家5月份各项支出与总支出的关系,适合用扇形统计图,排除;
D.商场8月份五种不同商品的销售额占总销售额的百分之几,适合用扇形统计图,排除。
故答案为:A
【点睛】关键是熟悉各种统计图的特点,根据统计图的特点进行分析。
6.(1)2010年至2013年每一年的具体人数情况
(2)2010年至2013年每一年的人数变化情况
(3)2010年至2013年每一年的人数占这4年总的人数的百分比情况
【分析】条形统计图可以看出数据情况,折线统计图可以反映数据的变化情况,扇形统计图可以反映各个部分数量和总量之间的关系。据此,再结合题中数据的具体情景,分析填空即可。
【详解】(1)从条形统计图中,我们可以清楚地看出:2010年至2013年每一年的具体人数情况。
(2)从折线统计图中,我们可以清楚地看出:2010年至2013年每一年的人数变化情况。
(3)从扇形统计图中,我们可以清楚地看出:2010年至2013年每一年的人数占这4年总的人数的百分比情况。
【点睛】掌握条形统计图、折线统计图以及扇形统计图的特点是解题的关键。
7.(1)9
(2)16
(3)550
【分析】(1)将六年级参加综合素质评价的全体学生人数看作单位“1”,用总体减去综合素质为A、B和C的学生所占的百分数,所得结果即为综合素质为D的学生占的百分数;
(2)用减法计算综合素质为B的学生和综合素质为A的学生的所占的百分数之差,再根据求一个数的百分之几是多少,用乘法计算;
(3)将六年级参加综合素质评价的学生看作单位“1”,其中综合素质为C的学生占12%,也就是66人,要求全体学生人数,用除法计算。
【详解】(1)1-(37%+42%+12%)
=1-91%
=9%
所以综合素质为D的学生占9%。
(2)320×(42%-37%)
=320×5%
=16(人)
所以综合素质为B的学生比综合素质为A的学生多16人。
(3)66÷12%=550(名)
所以如果综合素质为C的学生有66人,那么六年级有550名学生参加综合素质评价。
【点睛】解答本题的关键是理解掌握扇形统计图的特点,并且能够根据统计图提供的信息,解决相关问题。
8. 六(1)班各种类型体重的具体学生人数 六(1)班各种类型体重的人数占总人数的百分比
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】面的两幅统计图都表示六(1)班学生的体重情况。从左下图可以很容易看出六(1)班各种类型体重的具体学生人数,从右下图可以清楚地看出六(1)班各种类型体重的人数占总人数的百分比。例如:六(1)班营养不良的有5人,占六(1)班学生人数的15.6%。
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
9. 1600 800 1000 200 4000 10%
【分析】根据扇形统计图求出水电费用所占的百分比,用水电费用400元除以其对应分率,即可求出小红家五月份支出及储蓄总额,进一步求出各项费用即可。
【详解】水电费用所占的百分比:
1-40%-20%-25%-5%=10%
合计:400÷10%=4000(元)
伙食费用:4000×40%=1600(元)
购物费用:4000×20%=800(元)
储蓄:4000×25%=1000(元)
其他:4000×5%=200(元)
【点睛】本题考查扇形统计图的综合应用。已知一个数的几(百)分之几是多少,求这个数,用除法计算;求一个数的百分之几是多少,用乘法计算。
10.(1)60
(2) 轮滑 24
(3)20
【分析】(1)把六年级同学参加运动的总人数看作单位“1”,根据减法的意义,用1-20%-25%-40%即可求出参加花滑运动人数占总人数的百分比;已知参加花滑运动的有9人,根据百分数除法的意义,用9÷(1-20%-25%-40%)即可求出总人数;
(2)比较每项运动占的百分比,发现参加轮滑运动的人数最多,根据百分数乘法的意义,用总人数乘40%即可求出参加轮滑运动的人数;
(3)根据求一个数比另一个数少百分之几,用相差数除以另一个数再乘100%,则用(25%-20%)÷25%×100%即可求出参加旱地冰壶运动的人数比参加雪地足球运动的少百分之几。
【详解】(1)1-20%-25%-40%=15%
9÷15%=60(人)
六年级共有60人参加了冰雪运动。
(2)15%<20%<25%<40%
参加轮滑运动的人数最多,有24人。
(3)(25%-20%)÷25%×100%
=5%÷25%×100%
=20%
参加旱地冰壶运动的人数比参加雪地足球运动的少20%。
【点睛】此题考査的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
11.(1)100
(2) 乒乓 50
(3) 2 10
(4)60
【分析】(1)把全班学生人数看作单位“1”,六(2)班喜欢球类的人数占全班总人数的百分比之和应该是100%。
(2)通过观察统计图可知,比较喜欢乒乓球、篮球、足球、羽毛球占全班总人数的百分比的大小,即可求出喜欢乒乓球的人数最多,占全班人数的50%。
(3)根据求一个数的百分之几是多少,用乘法解决,用总人数分别乘喜欢足球、喜欢篮球的人数占总人数的百分比,即可求出喜欢足球和喜欢篮球的人数各是多少。
(4)把全班学生人数看作单位“1”,喜欢羽毛球的有12人,占全班人数的20%,已知一个数的百分之几是多少,求这个数,用除法解答。
【详解】(1)50%+25%+5%+20%=100%
六(2)班喜欢球类的人数占全班总人数的百分比之和应该是100%。
(2)5%<20%<25%<50%
喜欢乒乓球的人数最多,占全班人数的50%。
(3)40×5%=2(人)
40×25%=10(人)
喜欢足球的有2人,喜欢篮球的有10人。
(4)12÷20%=60(人)
六(2)班一共有60人。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
12.×
【分析】条形统计图用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;扇形统计图中用整个圆表示总数量,圆内各个扇形的大小表示各部分数量占总数量的百分比,通过扇形统计图可以清楚地看出各部分数量与总数量之间,部分数量与部分数量之间的关系,据此解答。
【详解】分析可知,小明记录分析自己各单元数学测试成绩的波动情况,用折线统计图比较合适。
故答案为:×
【点睛】本题主要考查统计图的选择,掌握各统计图的特点及作用是解答题目的关键。
13.×
【分析】扇形统计图中用整个圆表示总数量,圆内各个扇形的大小表示各部分数量占总数量的百分比,通过扇形统计图可以清楚地看出各部分数量与总数量之间,各项的百分比之和不能超过100%,据此解答。
【详解】69.4%+51.2%=120.6%
因为120.6%>100%,也就是说被调查的学生中,有同时选择两项或两项以上的,所以不能用扇形统计图表示某小学学生用手机查资料的人数和玩游戏的人数占总人数的百分率。
故答案为:×
【点睛】掌握扇形统计图的特点及作用是解答题目的关键。
14.√
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】根据分析可知,要反映某地区2022年全年降水量的变化情况,应绘制折线统计图。原题干说法正确。
故答案为:√
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
15.√
【分析】根据条形统计图、折线统计图、扇形统计图的特征分析题中说法是否正确即可。
【详解】条形统计图:用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;
折线统计图:不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;
扇形统计图:扇形统计图可以清楚地看出各部分数量与总数量之间,部分数量与部分数量之间的关系;
由上可知,题中说法正确。
故答案为:√
【点睛】理解并掌握各统计图的特征是解答题目的关键。
16.见详解
【分析】将总人数看作单位“1”,没有剩的人数÷对应百分率=总人数,总人数-剩一半的人数-剩大量的人数=剩少量的人数,据此补充条形统计图;分别用剩少量、剩一半、剩大量的人数除以总人数,求出剩少量、剩一半、剩大量的对应百分率,补充扇形统计图即可。
【详解】100÷50%=200(人)
200-100-30-20=50(人)
50÷200=0.25=25%
30÷200=0.15=15%
20÷200=0.1=10%
如图所示:
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数相关解题思路解答即可。
17.96万平方千米
【分析】把我国国土面积看作单位“1”,用单位“1”减去山地、高原、盆地、平原占国土面积的百分率,即可求出丘陵占国土的百分率,再根据求一个数的百分之几是多少,用乘法计算即可。
【详解】960×(1-33%-26%-19%-12%)
=960×10%
=96(万平方千米)
答:我国丘陵面积有96万平方千米。
【点睛】本题考查求一个数的百分之几是多少,明确用乘法是解题的关键。
18.(1)200人
(2)篮球比赛,理由见详解
【分析】(1)由题意可知,喜欢乒乓球的人数占总人数的15%,有60人,根据已知一个数的百分之几是多少,求这个数,用除法计算,用60除以15%求出总人数,再根据求一个数的百分之几是多少,用乘法计算,用总人数乘50%即可求出喜欢篮球运动的有多少人;
(2)通过扇形统计图可知,喜欢篮球的人数多,则应该组织篮球比赛。
【详解】(1)60÷15%×50%
=400×50%
=200(人)
答:喜欢篮球运动的有200人。
(2)应该组织篮球比赛,因为喜欢篮球的人数多。
【点睛】本题考查已知一个数的百分之几是多少,求这个数,明确用除法是解题的关键。
19.224件
【分析】140型号的博士服的数量占六年级毕业生博士服总套数的8%,其中140型号的博士服需要做64件,已知一个数的百分之几是多少,求这个数,用除法,用64除以8%,求出博士服的总数量,再乘150型号的博士服数量占总数量的28%,即可求出150型号的博士服需要做多少件。
【详解】64÷8%×28%
=64÷0.08×0.28
=800×0.28
=224(件)
答:150型号的博士服需要做224件。
【点睛】此题的解题关键是理解扇形统计图的特点,掌握求一个数的百分之几是多少和已知一个数的百分之几是多少,求这个数的计算方法。
20.(1)25人;
(2)20%;
(3)10%;
(4)见详解
【分析】(1)把六年级一班的总人数看作单位“1”,80—90分以下的占全班人数的50%,则90分及以上、60—80分以下、60分以下一共占总人数的(1-50%),根据量÷对应的百分率=单位“1”求出六年级一班的总人数,80—90分以下的人数=总人数×50%;
(2)六年级一班的优生率=90分及以上的人数÷六年级一班的总人数×100%;
(3)六年级一班的不合格率=60分以下的人数÷六年级一班的总人数×100%;
(4)扇形统计图中用整个圆表示总数量,圆内各个扇形的大小表示各部分数量占总数量的百分比,90分及以上的人数占总人数的20%,80—90分以下的人数占总人数的50%,60—80分以下的人数与90分及以上的人数相同,都占总人数的20%,60分以下的人数占总人数的10%,据此解答。
【详解】(1)(10+10+5)÷(1-50%)
=25÷0.5
=50(人)
50×50%=25(人)
所以,80—90分以下的有25人。
分数 90分及以上 80—90分以下 60—80分以下 60分以下
人数 10人 25人 10人 5人
(2)10÷50×100%
=0.2×100%
=20%
答:六年级一班的优生率是20%。
(3)5÷50×100%
=0.1×100%
=10%
答:六年级一班的不合格率是10%。
(4)分析可知:
【点睛】根据量和对应的百分率求出总人数,并掌握一个数占另一个数百分之几的计算方法以及扇形统计图的特点和作用是解答题目的关键。
21.(1)200
(2)60
(3)10
(4)见详解
(5)见详解
【分析】(1)结合两幅统计图可知,步行的教师有36人占调查总人数的18%,把调查的总人数看作单位“1”,根据已知一个数的百分之几是多少,求这个数,用除法计算,即可求出总人数。
(2)把调查的总人数看作单位“1”,已知坐公交车的教师人数占总人数的30%,根据求一个数的百分之几是多少,用乘法计算,即可求出坐公交车的教师人数。
(3)用开车的教师人数除以总人数,即可求出开车的人数占总人数百分之几。
(4)根据第(2)(3)题的数据,将条形统计图和扇形统计图补充完整。
(5)结合两幅统计图中的信息,写出自己的见解,合理即可。
【详解】(1)36÷18%
=36÷0.18
=200(名)
一共调查了200名教师。
(2)200×30%
=200×0.3
=60(人)
坐公交的有60人。
(3)20÷200×100%
=0.1×100%
=10%
开车的占10%。
(4)如图:
(5)我认为这所学校的教师在“绿色出行”方面做得好,大部分教师都选择了绿色出行方式。(答案不唯一)
【点睛】本题考查统计图的综合应用,掌握条形统计图、扇形统计图的特点及作用,从统计图中获取信息,并根据获取的信息解决有关的实际问题。
22.(1)2000
(2)45;900;见详解
(3)见详解
【分析】(1)从两幅统计图中可知,每天使用手机1~3小时的有360人,占全部接受调查人数的18%,把接受调查的总人数看作单位“1”,根据已知一个数的百分之几是多少,求这个数,用除法计算,即可求出接受调查的总人数。
(2)先用每天使用手机1小时以内的40人除以接受调查的总人数,求出每天使用手机1小时以内的人数占总人数的百分比。
把接受调查的总人数看作单位“1”,根据减法的意义,用“1”分别减去已知的每天使用手机的各时间段人数占总人数的百分比,即是每天使用手机5小时以上的占全部接受调查人数的百分比。
根据求一个数的百分之几是多少,用总人数乘每天使用手机5小时以上的百分比,即可求出每天使用手机5小时以上的人数。
据此将条形统计图补充完整。
(3)结合统计图中的信息,提出建议,合理即可。
【详解】(1)360÷18%
=360÷0.18
=2000(人)
接受调查的一共有2000人。
(2)40÷2000×100%
=0.02×100%
=2%
1-2%-18%-35%=45%
2000×45%
=2000×0.45
=900(人)
每天使用手机5小时以上的占全部受调查人数的45%,有900人。
如图:
(3)我建议:①合理安排好手机使用时间,做到上网生活两不误。②平时多参加体育锻炼和课外活动,每天有计划地看看绿色植物,放松眼睛。(答案不唯一)
【点睛】本题考查统计图的综合应用,掌握条形统计图和扇形统计图的特点和作用,从统计图中获取信息,根据获取的信息解决有关的实际问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
