人教版六年级数学上册第七单元扇形统计图(知识点梳理+能力百分练)三(含答案)
文档属性
| 名称 | 人教版六年级数学上册第七单元扇形统计图(知识点梳理+能力百分练)三(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 827.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 14:57:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版六年级数学上册第七单元扇形统计图(知识点梳理+能力百分练)三
知识点梳理
1、扇形统计图的意义:用整个圆的面积表示总数,用圆内各个扇形面积表示各部分数量同总数之间的关系,也就是各部分数量占总数的百分比。
2、常用统计图的优点:条形统计图;可以清楚的看出各种数量的多少;折线统计图:不仅可以看出各种数量的多少,还可以清晰看出数量的增减变化情况;扇形统计图;能够清楚的反映出各部分数量同总数之间的关系。
能力百分练
一、选择题(共10分)
1.李老师要对全班同学的成绩进行统计,你觉得选用( )统计最合适。
A.条形统计图 B.折线统计图 C.扇形统计图 D.统计表
2.下表是金昌市2018-2022年常住人口数统计表。六年级李月同学很想了解近5年金昌市的人口变化趋势,绘制成( )比较合适。
年份 2022 2021 2020 2019 2018
人口数/万人 43.53 43.5 43.8 44.1 44.4
A.条形统计图 B.折线统计图 C.扇形统计图 D.以上三种统计图
3.春节期间,某小学就学生对春节文化习俗的了解情况进行随机调查,了解程度为:A很了解、B比较了解、C了解较少、D不了解;并将调查结果绘制成下图所示不完整的统计图。下列说法错误的是( )
A.本次一共调查了400人 B.“比较了解”的人数最多
C.“不了解”的人数最少 D.“了解较少”的有80人
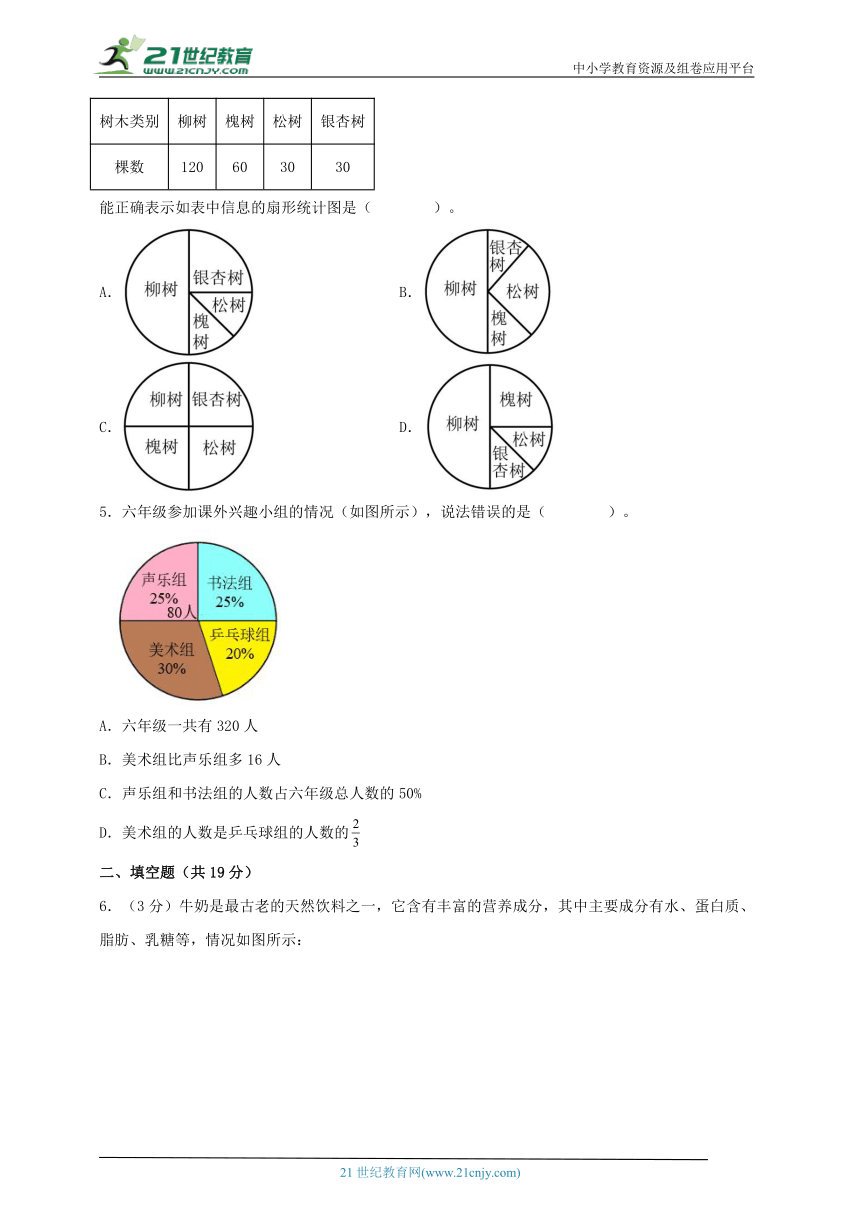
4.滨河公园四种树木棵数统计如表。
树木类别 柳树 槐树 松树 银杏树
棵数 120 60 30 30
能正确表示如表中信息的扇形统计图是( )。
A. B.
C. D.
5.六年级参加课外兴趣小组的情况(如图所示),说法错误的是( )。
A.六年级一共有320人
B.美术组比声乐组多16人
C.声乐组和书法组的人数占六年级总人数的50%
D.美术组的人数是乒乓球组的人数的
二、填空题(共19分)
6.(3分)牛奶是最古老的天然饮料之一,它含有丰富的营养成分,其中主要成分有水、蛋白质、脂肪、乳糖等,情况如图所示:
① ② ③ ④
(1)观察统计图,100克牛奶中的蛋白质、脂肪、乳糖三种营养成分,( )含量最高。
(2)蛋白质的含量占100克牛奶质量的( )%。
(3)上面的四幅扇形统计图中能反映条形统计图结果的是( )。
7.(3分)在习总书记“既要金山银山,又要绿水青山”思想的指导下,我国雾霾天气得到了较大改善。某校在学生申做了一次对雾霾知识了解程度的抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解。根据调查结果,绘制了如图所示的不完整的统计图。
结合统计图,回答下列问题:
(1)本次参与调查的学生一共有( )人。
(2)达到“基本了解”的同学占( )%。
(3)参与调查的学生中对雾霾情况“非常了解”的人数比“比较了解”的人数少( )%。
8.(4分)下图是六(1)班同学最喜欢喝的饮料情况统计图。
(1)最喜欢喝( )的人数最多,占全班总人数的( )%。
(2)如果全班有40人,那么最喜欢喝奶茶的有( )人。
(3)如果最喜欢喝可乐的有9人,那么全班有( )人。
9.(3分)下图所示,六(1)班参加三类球的人数统计情况如图。
(1)图中参加篮球人数所占的扇形的圆心角是( )°。
(2)六(1)班参加足球、篮球、排球人数的最简整数比是( )。
(3)参加排球的有8人,六(1)班参加三类球的总人数是( )人。
10.下图是六年级有关“垃圾分类”知识竞赛获奖情况统计图。
(1)这是一幅( )统计图。
(2)若参加这次竞赛获奖的一共有25人,获三等奖的有( )人。
11.(4分)如图是新苗小学六(1)班期末考试数学成绩统计图。
(1)这是一个( )统计图。
(2)得差人数占全班的( )%。
(3)已知得优的有12人,这个班共( )人,得良的比得可得多( )人。
三、判断题(共8分)
12.要了解各种支出占总支出的百分比情况,可选择折线统计图。( )
13.扇形统计图表示各部分数量与总数的关系,用整个圆表示总数。( )
14.扇形统计图可以表示某地一年气温的变化情况。( )
15.
从统计表中可看出,槐树棵数一定最少。( )
四、作图题(共6分)
16.(6分)为开展经典诵读活动,学校购买了一批图书。如图是购买的图书情况统计图,根据信息请将条形统计图和扇形统计图补充完整。
五、解答题(共57分)
17.(6分)2018年某镇花卉销售额共计900万元,各种花的销售情况如下图所示,请根据统计图完成下列问题。
(1)图中了解到( )的销售额最多,销售( )万元。
(2)玫瑰花的销售额比百合花多百分之几?
18.(6分)下图是李红上周的消费情况统计图,根据图中信息回答下面问题。
(1)李红上周一共用了200元,她买文具花了多少钱?
(2)李红上周的餐费比车费多百分之几?
19.(6分)我国五种基本地形所占国土面积百分比如图。其中丘陵的面积是96万平方千米,我国平原的面积是多少万平方千米?
20.(6分)淘气家这个月的支出情况如下图所示。食品支出比房贷支出多200元,淘气家这个月的教育支出是多少元?
21.(11分)周六上午,多多从学校先骑自行车到博物馆参加机器人展览活动,再乘公交车回家,行程描述如下图:
(1)若①表示骑自行车的时间,②表示参观活动的时间,③表示乘公交车回家的时间,请把上面的扇形统计图补充完成。
(2)多多骑自行车平均每分钟多少千米?
(3)多多从博物馆坐公交车回家,用了多少时间?
22.(11分)联合国规定每年的6月5日是“世界环境日”,环保组织对某社区开展了以“爱护环境,从我做起”为主题的问卷调查活动,并将调查结果按照以下三类垃圾处理方式整理后,制成了下面两个统计图。
A:能将垃圾放到规定地点,并会考虑垃圾分类。
B:能将垃圾放到规定地点,但不会考虑垃圾分类。
C:基本能将垃圾放到规定地点,偶尔会乱扔垃圾。
请你根据以上信息完成下面各题。
(1)图(1)是( )统计图,处理方式为C的占调查总人数的( )%。
(2)环保组织在某社区一共调查了( )人。
(3)请你将统计图(2)补充完整。
(4)不会乱扔垃圾的一共有( )人。
23.(11分)王老师调查了某地区甲、乙两校部分六年级学生平均每周使用手机时间的情况,绘制了如下不完整的统计表和统计图。
某地区甲、乙两校六年级学生平均每周使用手机时间情况统计表
(1)把上面的统计表和统计图补充完整。
(2)在参加调查统计的甲校学生人数中,平均每周使用手机时间在30分钟及以内的人数占( )%;在参加调查统计的乙校学生人数中,平均每周使用手机时间在120分钟以上的人数占( )%。
(3)你每周使用手机的时间约是多少分钟?请你结合实际对六年级学生使用手机提出合理化建议。
参考答案
1.D
【分析】条形统计图可以清楚地看出数量的多少;
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况;
扇形统计图表示各部分数量与总数之间的关系;
统计表容易看出数量的多少。
【详解】李老师要对全班同学的成绩进行统计,因为人数较多,且只需要看成绩的多少,我觉得选用统计表统计最合适。
故答案为:D
【点睛】掌握统计表、条形统计图、折线统计图、扇形统计图的特点是选择统计图表的关键。
2.B
【分析】条形统计图用直条的长短表示数量的多少,数据的大小;
折线统计图可以通过折线的上升或下降来清楚表示数量增减变化的情况;
扇形统计图:以一个圆的面积表示事物的总体,以扇形面积表示各部分占总体的百分数的统计图,叫做扇形统计图;
因为本题中,李月同学想了解近5年金昌市的人口变化趋势,只有折线统计图能够显示出这种变化的趋势,因此绘制成折线统计图比较合适。
【详解】由分析得:
六年级李月同学很想了解近5年金昌市的人口变化趋势,绘制成(折线统计图)比较合适。
故答案为:B
【点睛】考查了统计图的选择,需要明确各种统计图的特点,再结合具体题意来选择。
3.D
【分析】扇形统计图是以一个圆的面积(看作单位“1”)表示物体的总数量,以相应的扇形面积占整个圆面积的百分数表示各有关部分占总数量的百分数的统计图。比较A、B、C、D各部分扇形面积的大小即可看出,B>A>C>D,所以“比较了解”的人数最多,“不了解”的人数最少;已知一个数的百分之几是多少,求这个数,用除法,求出本次一共调查的人数,再用调查的总人数减去“很了解”、“比较了解”、“不了解”的人数,即可求出“了解较少”的人数。据此解答。
【详解】A.200÷50%=400(人),即本次一共调查了400人;
B.根据分析得,“比较了解”的人数最多;
C.根据分析得,“不了解”的人数最少;
D.400-120-200-20=60(人),即“了解较少”的有60人。
故答案为:D
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
4.D
【分析】先求出四种树木的总棵数,然后分别用柳树、槐树、松树、银杏树的棵数除以总棵数,求出它们占总棵数的百分比,再对照四幅扇形统计图进行比较,得出结论。
【详解】总棵数:120+60+30+30=240(棵)
柳树:
120÷240×100%
=0.5×100%
=50%
槐树:
60÷240×100%
=0.25×100%
=25%
松树、银杏树:
30÷240×100%
=0.125×100%
=12.5%
A.,槐树不是25%,银杏树不是12.5%,且没有和松树一样多,不符合题意;
B.,槐树不是25%,松树不是12.5%,且没有和银杏树一样多,不符合题意;
C.,柳树不是50%,银杏树和松树都不是12.5%,不符合题意;
D.,柳树是50%,槐树是25%,银杏树和松树一样多,都是12.5%,符合题意。
故答案为:D
【点睛】本题考查百分数的应用,掌握扇形统计图的特点及作用,明确求一个数是另一个数的百分之几是多少,用除法计算。
5.D
【分析】(1)把六年级的总人数看作单位“1”,单位“1”未知用除法计算。声乐组的人数80人所对应的分率是25%,用80÷25%可求出总人数是320人。
(2)美术组占总人数的30%,求一个数的百分之几是多少用乘法计算,据此用320×30%求出美术组的人数,再减去声乐组的人数80人,可求出美术组比声乐组多的人数。
(3)用声乐组占的百分率+书法组所占的百分率可求出二者共占六年级总人数的百分率。
(4)用美术组占的百分率÷乒乓球组所占的百分率可求出美术组的人数是乒乓球组的人数的几分之几。
【详解】A.80÷25%=80÷=80×4=320(人),所以六年级一共有320人。A选项正确。
B.320×30%-80=96-80=16(人),所以美术组比声乐组多16人。B选项正确。
C.25%+25%=50%,所以声乐组和书法组的人数占六年级总人数的50%。C选项正确。
D.30%÷20%=0.3÷0.2=3÷2=,≠。D选项错误。
故答案为:D
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数问题,按照百分数问题的解题思路和解题方法进行解答。
6.(1)乳糖
(2)3.3
(3)①
【分析】(1)通过观察统计图可知,100克牛奶中的蛋白质、脂肪、乳糖三种营养成分,乳糖含量最高;
(2)把100克牛奶的质量看作单位“1”,根据求一个数占另一个数的百分之几,用除法解答;
(3)根据求一个数是另一个数的百分之几,用除法分别求出各种成分所占的百分比,然后对照下面四幅图进行比较即可。
【详解】(1)4.8>4>3.3
100克牛奶中的蛋白质、脂肪、乳糖三种营养成分,乳糖含量最高。
(2)3.3÷100×100%=3.3%
蛋白质的含量占100克牛奶质量的3.3%。
(3)87÷100×100%=87%
4÷100×100%=4%
4.8÷100×100%=4.8%
0.9÷100×100%=0.9%
3.3÷100×100%=3.3%
能反映条形统计图结果的是图①。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
7.(1)400
(2)42
(3)87.5
【分析】(1)把调查的总人数看作单位“1”,不了解的有140人,占调查总人数的35%,根据已知一个数的百分之几是多少,求这个数,用除法解答;
(2)用比较了解的人数除以总人数,得出比较了解的人数占的百分率,再用减法计算即可得C部分基本了解占的百分率;
(3)用“比较了解”的人数减“非常了解”的人数,再除以“比较了解”的人数即可。
【详解】(1)140÷35%=400(人)
(2)80÷400×100%
=0.2×100%
=20%
1-3%-20%-35%
=97%-20%-35%
=77%-35%
=42%
(3)(80-10)÷80×100%
=70÷80×100%
=0.875×100%
=87.5%
【点睛】此题主要考查学生如何从扇形统计图、条形统计图中获取信息,然后再根据所获取的信息解决实际问题。
8.(1) 绿茶 30
(2)8
(3)60
【分析】(1)把总人数看作单位“1”,比较每个量对应的百分比即可;
(2)根据百分数乘法的意义,用40×20%即可求出最喜欢喝奶茶的人数;
(3)根据百分数除法的意义,用9÷15%即可求出全班总人数。
【详解】(1)30%>25%>20%>15%>10%
最喜欢喝绿茶的人数最多,占全班总人数的30%。
(2)40×20%=8(人)
如果全班有40人,那么最喜欢喝奶茶的有8人。
(3)9÷15%=60(人)
如果最喜欢喝可乐的有9人,那么全班有60人。
【点睛】此题考查的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
9.(1)135
(2)3∶3∶2
(3)32
【分析】(1)参加足球人数占参加三类球的总人数的37.5%,用360°乘参加足球人数占总人数的百分比,求出图中参加足球人数所占的扇形的圆心角,从图中可以看出参加排球人数所占的扇形的圆心角是90°,再用360°减去参加足球人数所占的扇形的圆心角和参加排球人数所占的扇形的圆心角,即可求出图中参加篮球人数所占的扇形的圆心角。
(2)用参加排球人数所占的扇形的圆心角除以360°,求出参加排球人数占总人数的百分比,用参加篮球人数所占的扇形的圆心角除以360°,求出参加篮球人数占总人数的百分比,再根据比的意义,用参加三种球类运动的人数所占的百分比相比,即可求出六(1)班参加足球、篮球、排球人数的最简整数比。
(3)已知一个数的百分之几是多少,求这个数,用除法,用参加排球的人数除以参加排球人数占总人数的百分比,即可求出六(1)班参加三类球的总人数。
【详解】(1)360°-360°×37.5%-90°
=360°-135°-90°
=135°
即图中参加篮球人数所占的扇形的圆心角是135°。
(2)135°÷360°=0.375=37.5%
90°÷360°=0.25=25%
37.5%∶37.5%∶25%
=0.375∶0.375∶0.25
=∶∶
=3∶3∶2
即六(1)班参加足球、篮球、排球人数的最简整数比是3∶3∶2。
(3)8÷25%
=8÷0.25
=32(人)
即六(1)班参加三类球的总人数是32人。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
10.(1)扇形
(2)15
【分析】(1)条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
(2)把竞赛获奖的总人数看作单位“1”,根据减法的意义,用1-15%-25%即可求出获三等奖的人数占总人数的百分之几;再根据百分数乘法的意义,用25×(1-15%-25%)即可求出获三等奖的人数。
【详解】(1)这是一幅扇形统计图。
(2)25×(1-15%-25%)
=25×60%
=15(人)
若参加这次竞赛获奖的一共有25人,获三等奖的有15人。
【点睛】此题考查的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
11.(1)扇形
(2)5
(3) 40 6
【分析】(1)通过观察统计图直接回答问题。
(2)把全班人数看作单位“1”,根据减法的意义,用减法解答。
(3)把全班人数看作单位“1”,其中得优的有12人,占全班人数的30%,根据已知一个数的百分之几是多少,求这个数,用除法求出全班人数,再根据求一个数的百分之几是多少,用乘法求出得良的比得可得多多少人。
【详解】(1)由图可知:这是一幅扇形统计图。
(2)1-30%-40%-25%=5%
(3)12÷30%=40(人)
40×(40%-25%)
=40×15%
=6(人)
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
12.×
【分析】条形统计图可以清楚地看出数量的多少;
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况;
扇形统计图表示各部分数量与总数之间的关系。
【详解】要了解各种支出占总支出的百分比情况,可选择扇形统计图。
原题说法错误。
故答案为:×
【点睛】理解掌握条形统计图、折线统计图、扇形统计图的特点是选择统计图的关键。
13.√
【分析】扇形统计图是以一个圆的面积(看作单位“1”)表示物体的总数量,以相应的扇形面积占整个圆面积的百分数表示各有关部分占总数量的百分数的统计图。
【详解】扇形统计图表示各部分数量与总数的关系,用整个圆表示总数,说法正确。
故答案为:√
【点睛】扇形统计图清楚地看出各部分数量与总数量之间,部分与部分之间的关系。
14.×
【分析】要表示一年气温数据的变化情况,根据折线统计图、扇形统计图的特点,并结合实际问题,进行判断。
【详解】折线统计图能直观的表示出数量随时间的变化趋势,扇形统计图能表示出部分数量与总数之间的关系,因此能够表示某地一年气温的变化情况的应该是折线统计图。
故答案为:×
【点睛】考查根据实际情况选择合适的统计图分析数据。
15.×
【分析】由统计表可知:柳树、杨树、槐树和其他的棵树,其他表示除了柳树、杨树、槐树以外的的树种,所以并不能说明槐树最少。据此解答即可。
【详解】由分析可知:
除了柳树、杨树、槐树,还有其他的树种,所以槐树不一定最少。故题干说法错误。
【点睛】本题考查统计表的实际应用,通过统计表分析出相应的数据是解题的关键。
16.见详解。
【分析】把购买图书的总数看作单位“1”,科技书和连环画的本数占总数的(1-30%-5%),科技书和连环画的总本数是(320+200)本,根据已知一个数的百分之几是多少,求这个数,先用除法求出总数;再根据求一个数的百分之几是多少,用乘法分别求出故事书的本数、其他书的本数;再根据求一个数是另一个数的百分之几,用除法求出科技书、连环画各占总数的百分之几。据此完成统计图。
【详解】图书的总本数:(320+200)÷(1-30%-5%)
=520÷65%
=520÷0.65
=800(本)
故事书的本数:800×30%=240(本)
其他书的本数:800×5%=40(本)
科技书占总数的分率:320÷800
=0.4
=40%
连环画占总数的分率:200÷800
=0.25
=25%
作图如下:
【点睛】此题考查的目的是理解掌握条形统计图、扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
17.(1)康乃馨;405
(2)25%
【分析】(1)根据扇形统计图,康乃馨的占比最多。将100%减去百合、玫瑰以及其它的百分比,求出康乃馨的百分比。将总的销售额900万元乘康乃馨的百分比,即可求出康乃馨的具体销售额;
(2)将总的销售额看作单位“1”,利用乘法分别求出玫瑰花和百合花的销售额,并利用减法求出两种花的销售额的差。将销售额差除以百合花的销售额,即可求出玫瑰花的销售额比百合花多百分之几。
【详解】(1)900×(100%―20%―25%―10%)
=900×45%
=405(万元)
所以,康乃馨的销售额最多,销售405万元。
(2)900×25%=225(万元)
900×20%=180(万元)
(225―180)÷180
=45÷180
=25%
答:玫瑰花的销售额比百合花多25%。
【点睛】本题考查了扇形统计图的应用,能从扇形统计图中获取信息,并掌握百分数的运算是解题关键。
18.(1)20元
(2)40%
【分析】(1)把李红上周总的消费200元看作单位“1”,买文具的费用占10%。求一个数的百分之几是多少的问题的解法:一个数(单位“1”的量)×百分率=部分量。据此求买文具花的钱可列式为200×10%。
(2)求一个数比另一个数多百分之几的问题的解法:相差的量÷单位“1”的量。先用李红上周总的消费×35%求出餐费的钱数;再用李红上周总的消费×25%求出车费的钱数;最后用(餐费的钱数-车费的钱数)÷车费的钱数,求出李红上周的餐费比车费多百分之几。
【详解】(1)200×10%=20(元)
答:她买文具花了20元。
(2)(200×35%-200×25%)÷(200×25%)
=(70-50)÷50
=20÷50
=40%
答:李红上周的餐费比车费多40%。
【点睛】注意求餐费比车费多百分之几时,不能用35%-25%,因为单位“1”是车费的钱数而不是李红上周的总费用。
19.115.2万平方千米
【分析】把我国国土总面积看作单位“1”,丘陵的面积是96万平方千米,占10%,由此用除法即可求出我们国土总面积,进而把我国国土总面积看作单位“1”,平原占的百分率是12%,求我国平原的面积,根据一个数乘分数的意义,用乘法解答即可。
【详解】96÷10%
=96÷0.1
=960(万平方千米)
960×12%
=960×0.12
=115.2(万平方千米)
答:我国平原的面积是115.2万平方千米。
【点睛】此题是考查如何观察扇形统计图,并从扇形统计图中获取信息,然后再根据所获取的信息解决实际问题。
20.1200元
【分析】淘气家这个月的总支出额看作单位“1”,根据已知一个数的百分之几是多少,求这个数,用除法求出总支出,再根据求一个数的百分之几是多少,用乘法解答。
【详解】200÷(25%-20%)×30%
=200÷0.05×0.3
=4000×0.3
=1200(元)
答:淘气家这个月的教育支出是1200元。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
21.(1)见详解;(2)0.2千米;(3)10分钟
【分析】(1)观察折线统计图可知,骑自行车的时间是8分钟,参观活动的时间是(30-8)分钟,明显参观活动时间大于骑自行车时间,所以扇形统计图上面的括号填①,下面的括号填②;
(2)观察题意可知,多多骑自行车骑了(3-1.4)千米,根据速度=路程÷时间,用(3-1.4)÷8即可求出多多骑自行车平均每分钟多少千米;
(3)把多多所花的总时间看作单位“1”,观察扇形统计图可知,乘公交车回家的时间占总时间的,则骑自行车的时间和参观活动的时间一共占总时间的(1-),根据分数除法的意义,用30÷(1-)即可求出总时间,然后用总时间减去30分钟,即可求出乘公交车回家的时间。
【详解】(1)30-8=22(分钟)
22>8
扇形统计图如下:
(2)(3-1.4)÷8
=1.6÷8
=0.2(千米)
答:多多骑自行车平均每分钟0.2千米。
(3)30÷(1-)
=30÷
=30×
=40(分钟)
40-30=10(分钟)
答:多多从博物馆坐公交车回家,用了10分钟。
【点睛】此题考查的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
22.(1)扇形;5
(2)2400
(3)图形见详解
(4)2280
【分析】(1)根据统计图的特点,可知图(1)是扇形统计图,把调查的总人数看作单位“1”,根据减法的意义,用减法解答。
(2)把调查的总人数看作单位“1”,根据已知一个数的百分之几是多少,求这个数,用除法解答。
(3)根据求一个数的百分之几是多少,用乘法分别求出B、C的人数,据此完成条形统计图。
(4)根据减法的意义,用调查的总人数减去C的人数就是不会乱扔垃圾的人数。
【详解】(1)1-50%-45%
=50%-45%
=5%
则图(1)是扇形统计图,处理方式为C的占调查总人数的5%。
(2)1200÷50%
=1200÷05
=2400(人)
则环保组织在某社区一共调查了2400人。
(3)2400×45%=1080(人)
2400×5%=120(人)
作图如下:
(4)2400-120=2280(人)
则不会乱扔垃圾的一共有2280人。
【点睛】此题考查目的是理解掌握扇形统计图、条形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
23.(1)见详解
(2)10;5
(3)见详解
【分析】(1)分别用加法求出甲校、乙校的合计人数,把统计表补充完整;
观察乙校平均每周使用手机时间在30~60分钟人数为50人,占总人数100人的50%,左边的扇形统计图有占50%的扇形,而右边的扇形统计图中没有占比为50%的扇形,由此确定左边的扇形统计图是乙校的,那么右边的扇形统计图就是甲校的;再分别计算出两个学校各个时间段的人数占总人数的百分比,根据扇形面积的大小,把统计图补充完整。
(2)根据求一个数占另一个数的百分之几,用除法解答。
(3)结合自身情况以及统计图表的数据,对六年级学生使用手机提出建议,合理即可。
【详解】(1)甲校合计:10+20+40+20+10=100(人)
乙校合计:20+50+15+10+5=100(人)
甲校:
30分钟及以内占:10÷100×100%=10%
30~60分钟占:20÷100×100%=20%
60~90分钟占:40÷100×100%=40%
90~120分钟占:20÷100×100%=20%
120分钟以上占:10÷100×100%=10%
乙校:
30分钟及以内占:20÷100×100%=20%
30~60分钟占:50÷100×100%=50%
60~90分钟占:15÷100×100%=15%
90~120分钟占:10÷100×100%=10%
120分钟以上占:5÷100×100%=5%
某地区甲、乙两校六年级学生平均每周使用手机时间情况统计表
(2)10÷100×100%=10%
5÷100×100%=5%
在参加调查统计的甲校学生人数中,平均每周使用手机时间在30分钟及以内的人数占10%;
在参加调查统计的乙校学生人数中,平均每周使用手机时间在120分钟以上的人数占5%。
(3)我每周使用手机的时间约是90分钟。建议:不要过度依赖手机,要合理安排使用手机的时间。(答案不唯一)
【点睛】本题考核统计表和扇形统计图的综合应用,根据统计图表提供的信息,解决有关的实际问题。明确求一个数占另一个数的百分之几,用除法计算。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版六年级数学上册第七单元扇形统计图(知识点梳理+能力百分练)三
知识点梳理
1、扇形统计图的意义:用整个圆的面积表示总数,用圆内各个扇形面积表示各部分数量同总数之间的关系,也就是各部分数量占总数的百分比。
2、常用统计图的优点:条形统计图;可以清楚的看出各种数量的多少;折线统计图:不仅可以看出各种数量的多少,还可以清晰看出数量的增减变化情况;扇形统计图;能够清楚的反映出各部分数量同总数之间的关系。
能力百分练
一、选择题(共10分)
1.李老师要对全班同学的成绩进行统计,你觉得选用( )统计最合适。
A.条形统计图 B.折线统计图 C.扇形统计图 D.统计表
2.下表是金昌市2018-2022年常住人口数统计表。六年级李月同学很想了解近5年金昌市的人口变化趋势,绘制成( )比较合适。
年份 2022 2021 2020 2019 2018
人口数/万人 43.53 43.5 43.8 44.1 44.4
A.条形统计图 B.折线统计图 C.扇形统计图 D.以上三种统计图
3.春节期间,某小学就学生对春节文化习俗的了解情况进行随机调查,了解程度为:A很了解、B比较了解、C了解较少、D不了解;并将调查结果绘制成下图所示不完整的统计图。下列说法错误的是( )
A.本次一共调查了400人 B.“比较了解”的人数最多
C.“不了解”的人数最少 D.“了解较少”的有80人
4.滨河公园四种树木棵数统计如表。
树木类别 柳树 槐树 松树 银杏树
棵数 120 60 30 30
能正确表示如表中信息的扇形统计图是( )。
A. B.
C. D.
5.六年级参加课外兴趣小组的情况(如图所示),说法错误的是( )。
A.六年级一共有320人
B.美术组比声乐组多16人
C.声乐组和书法组的人数占六年级总人数的50%
D.美术组的人数是乒乓球组的人数的
二、填空题(共19分)
6.(3分)牛奶是最古老的天然饮料之一,它含有丰富的营养成分,其中主要成分有水、蛋白质、脂肪、乳糖等,情况如图所示:
① ② ③ ④
(1)观察统计图,100克牛奶中的蛋白质、脂肪、乳糖三种营养成分,( )含量最高。
(2)蛋白质的含量占100克牛奶质量的( )%。
(3)上面的四幅扇形统计图中能反映条形统计图结果的是( )。
7.(3分)在习总书记“既要金山银山,又要绿水青山”思想的指导下,我国雾霾天气得到了较大改善。某校在学生申做了一次对雾霾知识了解程度的抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解。根据调查结果,绘制了如图所示的不完整的统计图。
结合统计图,回答下列问题:
(1)本次参与调查的学生一共有( )人。
(2)达到“基本了解”的同学占( )%。
(3)参与调查的学生中对雾霾情况“非常了解”的人数比“比较了解”的人数少( )%。
8.(4分)下图是六(1)班同学最喜欢喝的饮料情况统计图。
(1)最喜欢喝( )的人数最多,占全班总人数的( )%。
(2)如果全班有40人,那么最喜欢喝奶茶的有( )人。
(3)如果最喜欢喝可乐的有9人,那么全班有( )人。
9.(3分)下图所示,六(1)班参加三类球的人数统计情况如图。
(1)图中参加篮球人数所占的扇形的圆心角是( )°。
(2)六(1)班参加足球、篮球、排球人数的最简整数比是( )。
(3)参加排球的有8人,六(1)班参加三类球的总人数是( )人。
10.下图是六年级有关“垃圾分类”知识竞赛获奖情况统计图。
(1)这是一幅( )统计图。
(2)若参加这次竞赛获奖的一共有25人,获三等奖的有( )人。
11.(4分)如图是新苗小学六(1)班期末考试数学成绩统计图。
(1)这是一个( )统计图。
(2)得差人数占全班的( )%。
(3)已知得优的有12人,这个班共( )人,得良的比得可得多( )人。
三、判断题(共8分)
12.要了解各种支出占总支出的百分比情况,可选择折线统计图。( )
13.扇形统计图表示各部分数量与总数的关系,用整个圆表示总数。( )
14.扇形统计图可以表示某地一年气温的变化情况。( )
15.
从统计表中可看出,槐树棵数一定最少。( )
四、作图题(共6分)
16.(6分)为开展经典诵读活动,学校购买了一批图书。如图是购买的图书情况统计图,根据信息请将条形统计图和扇形统计图补充完整。
五、解答题(共57分)
17.(6分)2018年某镇花卉销售额共计900万元,各种花的销售情况如下图所示,请根据统计图完成下列问题。
(1)图中了解到( )的销售额最多,销售( )万元。
(2)玫瑰花的销售额比百合花多百分之几?
18.(6分)下图是李红上周的消费情况统计图,根据图中信息回答下面问题。
(1)李红上周一共用了200元,她买文具花了多少钱?
(2)李红上周的餐费比车费多百分之几?
19.(6分)我国五种基本地形所占国土面积百分比如图。其中丘陵的面积是96万平方千米,我国平原的面积是多少万平方千米?
20.(6分)淘气家这个月的支出情况如下图所示。食品支出比房贷支出多200元,淘气家这个月的教育支出是多少元?
21.(11分)周六上午,多多从学校先骑自行车到博物馆参加机器人展览活动,再乘公交车回家,行程描述如下图:
(1)若①表示骑自行车的时间,②表示参观活动的时间,③表示乘公交车回家的时间,请把上面的扇形统计图补充完成。
(2)多多骑自行车平均每分钟多少千米?
(3)多多从博物馆坐公交车回家,用了多少时间?
22.(11分)联合国规定每年的6月5日是“世界环境日”,环保组织对某社区开展了以“爱护环境,从我做起”为主题的问卷调查活动,并将调查结果按照以下三类垃圾处理方式整理后,制成了下面两个统计图。
A:能将垃圾放到规定地点,并会考虑垃圾分类。
B:能将垃圾放到规定地点,但不会考虑垃圾分类。
C:基本能将垃圾放到规定地点,偶尔会乱扔垃圾。
请你根据以上信息完成下面各题。
(1)图(1)是( )统计图,处理方式为C的占调查总人数的( )%。
(2)环保组织在某社区一共调查了( )人。
(3)请你将统计图(2)补充完整。
(4)不会乱扔垃圾的一共有( )人。
23.(11分)王老师调查了某地区甲、乙两校部分六年级学生平均每周使用手机时间的情况,绘制了如下不完整的统计表和统计图。
某地区甲、乙两校六年级学生平均每周使用手机时间情况统计表
(1)把上面的统计表和统计图补充完整。
(2)在参加调查统计的甲校学生人数中,平均每周使用手机时间在30分钟及以内的人数占( )%;在参加调查统计的乙校学生人数中,平均每周使用手机时间在120分钟以上的人数占( )%。
(3)你每周使用手机的时间约是多少分钟?请你结合实际对六年级学生使用手机提出合理化建议。
参考答案
1.D
【分析】条形统计图可以清楚地看出数量的多少;
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况;
扇形统计图表示各部分数量与总数之间的关系;
统计表容易看出数量的多少。
【详解】李老师要对全班同学的成绩进行统计,因为人数较多,且只需要看成绩的多少,我觉得选用统计表统计最合适。
故答案为:D
【点睛】掌握统计表、条形统计图、折线统计图、扇形统计图的特点是选择统计图表的关键。
2.B
【分析】条形统计图用直条的长短表示数量的多少,数据的大小;
折线统计图可以通过折线的上升或下降来清楚表示数量增减变化的情况;
扇形统计图:以一个圆的面积表示事物的总体,以扇形面积表示各部分占总体的百分数的统计图,叫做扇形统计图;
因为本题中,李月同学想了解近5年金昌市的人口变化趋势,只有折线统计图能够显示出这种变化的趋势,因此绘制成折线统计图比较合适。
【详解】由分析得:
六年级李月同学很想了解近5年金昌市的人口变化趋势,绘制成(折线统计图)比较合适。
故答案为:B
【点睛】考查了统计图的选择,需要明确各种统计图的特点,再结合具体题意来选择。
3.D
【分析】扇形统计图是以一个圆的面积(看作单位“1”)表示物体的总数量,以相应的扇形面积占整个圆面积的百分数表示各有关部分占总数量的百分数的统计图。比较A、B、C、D各部分扇形面积的大小即可看出,B>A>C>D,所以“比较了解”的人数最多,“不了解”的人数最少;已知一个数的百分之几是多少,求这个数,用除法,求出本次一共调查的人数,再用调查的总人数减去“很了解”、“比较了解”、“不了解”的人数,即可求出“了解较少”的人数。据此解答。
【详解】A.200÷50%=400(人),即本次一共调查了400人;
B.根据分析得,“比较了解”的人数最多;
C.根据分析得,“不了解”的人数最少;
D.400-120-200-20=60(人),即“了解较少”的有60人。
故答案为:D
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
4.D
【分析】先求出四种树木的总棵数,然后分别用柳树、槐树、松树、银杏树的棵数除以总棵数,求出它们占总棵数的百分比,再对照四幅扇形统计图进行比较,得出结论。
【详解】总棵数:120+60+30+30=240(棵)
柳树:
120÷240×100%
=0.5×100%
=50%
槐树:
60÷240×100%
=0.25×100%
=25%
松树、银杏树:
30÷240×100%
=0.125×100%
=12.5%
A.,槐树不是25%,银杏树不是12.5%,且没有和松树一样多,不符合题意;
B.,槐树不是25%,松树不是12.5%,且没有和银杏树一样多,不符合题意;
C.,柳树不是50%,银杏树和松树都不是12.5%,不符合题意;
D.,柳树是50%,槐树是25%,银杏树和松树一样多,都是12.5%,符合题意。
故答案为:D
【点睛】本题考查百分数的应用,掌握扇形统计图的特点及作用,明确求一个数是另一个数的百分之几是多少,用除法计算。
5.D
【分析】(1)把六年级的总人数看作单位“1”,单位“1”未知用除法计算。声乐组的人数80人所对应的分率是25%,用80÷25%可求出总人数是320人。
(2)美术组占总人数的30%,求一个数的百分之几是多少用乘法计算,据此用320×30%求出美术组的人数,再减去声乐组的人数80人,可求出美术组比声乐组多的人数。
(3)用声乐组占的百分率+书法组所占的百分率可求出二者共占六年级总人数的百分率。
(4)用美术组占的百分率÷乒乓球组所占的百分率可求出美术组的人数是乒乓球组的人数的几分之几。
【详解】A.80÷25%=80÷=80×4=320(人),所以六年级一共有320人。A选项正确。
B.320×30%-80=96-80=16(人),所以美术组比声乐组多16人。B选项正确。
C.25%+25%=50%,所以声乐组和书法组的人数占六年级总人数的50%。C选项正确。
D.30%÷20%=0.3÷0.2=3÷2=,≠。D选项错误。
故答案为:D
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数问题,按照百分数问题的解题思路和解题方法进行解答。
6.(1)乳糖
(2)3.3
(3)①
【分析】(1)通过观察统计图可知,100克牛奶中的蛋白质、脂肪、乳糖三种营养成分,乳糖含量最高;
(2)把100克牛奶的质量看作单位“1”,根据求一个数占另一个数的百分之几,用除法解答;
(3)根据求一个数是另一个数的百分之几,用除法分别求出各种成分所占的百分比,然后对照下面四幅图进行比较即可。
【详解】(1)4.8>4>3.3
100克牛奶中的蛋白质、脂肪、乳糖三种营养成分,乳糖含量最高。
(2)3.3÷100×100%=3.3%
蛋白质的含量占100克牛奶质量的3.3%。
(3)87÷100×100%=87%
4÷100×100%=4%
4.8÷100×100%=4.8%
0.9÷100×100%=0.9%
3.3÷100×100%=3.3%
能反映条形统计图结果的是图①。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
7.(1)400
(2)42
(3)87.5
【分析】(1)把调查的总人数看作单位“1”,不了解的有140人,占调查总人数的35%,根据已知一个数的百分之几是多少,求这个数,用除法解答;
(2)用比较了解的人数除以总人数,得出比较了解的人数占的百分率,再用减法计算即可得C部分基本了解占的百分率;
(3)用“比较了解”的人数减“非常了解”的人数,再除以“比较了解”的人数即可。
【详解】(1)140÷35%=400(人)
(2)80÷400×100%
=0.2×100%
=20%
1-3%-20%-35%
=97%-20%-35%
=77%-35%
=42%
(3)(80-10)÷80×100%
=70÷80×100%
=0.875×100%
=87.5%
【点睛】此题主要考查学生如何从扇形统计图、条形统计图中获取信息,然后再根据所获取的信息解决实际问题。
8.(1) 绿茶 30
(2)8
(3)60
【分析】(1)把总人数看作单位“1”,比较每个量对应的百分比即可;
(2)根据百分数乘法的意义,用40×20%即可求出最喜欢喝奶茶的人数;
(3)根据百分数除法的意义,用9÷15%即可求出全班总人数。
【详解】(1)30%>25%>20%>15%>10%
最喜欢喝绿茶的人数最多,占全班总人数的30%。
(2)40×20%=8(人)
如果全班有40人,那么最喜欢喝奶茶的有8人。
(3)9÷15%=60(人)
如果最喜欢喝可乐的有9人,那么全班有60人。
【点睛】此题考查的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
9.(1)135
(2)3∶3∶2
(3)32
【分析】(1)参加足球人数占参加三类球的总人数的37.5%,用360°乘参加足球人数占总人数的百分比,求出图中参加足球人数所占的扇形的圆心角,从图中可以看出参加排球人数所占的扇形的圆心角是90°,再用360°减去参加足球人数所占的扇形的圆心角和参加排球人数所占的扇形的圆心角,即可求出图中参加篮球人数所占的扇形的圆心角。
(2)用参加排球人数所占的扇形的圆心角除以360°,求出参加排球人数占总人数的百分比,用参加篮球人数所占的扇形的圆心角除以360°,求出参加篮球人数占总人数的百分比,再根据比的意义,用参加三种球类运动的人数所占的百分比相比,即可求出六(1)班参加足球、篮球、排球人数的最简整数比。
(3)已知一个数的百分之几是多少,求这个数,用除法,用参加排球的人数除以参加排球人数占总人数的百分比,即可求出六(1)班参加三类球的总人数。
【详解】(1)360°-360°×37.5%-90°
=360°-135°-90°
=135°
即图中参加篮球人数所占的扇形的圆心角是135°。
(2)135°÷360°=0.375=37.5%
90°÷360°=0.25=25%
37.5%∶37.5%∶25%
=0.375∶0.375∶0.25
=∶∶
=3∶3∶2
即六(1)班参加足球、篮球、排球人数的最简整数比是3∶3∶2。
(3)8÷25%
=8÷0.25
=32(人)
即六(1)班参加三类球的总人数是32人。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
10.(1)扇形
(2)15
【分析】(1)条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
(2)把竞赛获奖的总人数看作单位“1”,根据减法的意义,用1-15%-25%即可求出获三等奖的人数占总人数的百分之几;再根据百分数乘法的意义,用25×(1-15%-25%)即可求出获三等奖的人数。
【详解】(1)这是一幅扇形统计图。
(2)25×(1-15%-25%)
=25×60%
=15(人)
若参加这次竞赛获奖的一共有25人,获三等奖的有15人。
【点睛】此题考查的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
11.(1)扇形
(2)5
(3) 40 6
【分析】(1)通过观察统计图直接回答问题。
(2)把全班人数看作单位“1”,根据减法的意义,用减法解答。
(3)把全班人数看作单位“1”,其中得优的有12人,占全班人数的30%,根据已知一个数的百分之几是多少,求这个数,用除法求出全班人数,再根据求一个数的百分之几是多少,用乘法求出得良的比得可得多多少人。
【详解】(1)由图可知:这是一幅扇形统计图。
(2)1-30%-40%-25%=5%
(3)12÷30%=40(人)
40×(40%-25%)
=40×15%
=6(人)
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
12.×
【分析】条形统计图可以清楚地看出数量的多少;
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况;
扇形统计图表示各部分数量与总数之间的关系。
【详解】要了解各种支出占总支出的百分比情况,可选择扇形统计图。
原题说法错误。
故答案为:×
【点睛】理解掌握条形统计图、折线统计图、扇形统计图的特点是选择统计图的关键。
13.√
【分析】扇形统计图是以一个圆的面积(看作单位“1”)表示物体的总数量,以相应的扇形面积占整个圆面积的百分数表示各有关部分占总数量的百分数的统计图。
【详解】扇形统计图表示各部分数量与总数的关系,用整个圆表示总数,说法正确。
故答案为:√
【点睛】扇形统计图清楚地看出各部分数量与总数量之间,部分与部分之间的关系。
14.×
【分析】要表示一年气温数据的变化情况,根据折线统计图、扇形统计图的特点,并结合实际问题,进行判断。
【详解】折线统计图能直观的表示出数量随时间的变化趋势,扇形统计图能表示出部分数量与总数之间的关系,因此能够表示某地一年气温的变化情况的应该是折线统计图。
故答案为:×
【点睛】考查根据实际情况选择合适的统计图分析数据。
15.×
【分析】由统计表可知:柳树、杨树、槐树和其他的棵树,其他表示除了柳树、杨树、槐树以外的的树种,所以并不能说明槐树最少。据此解答即可。
【详解】由分析可知:
除了柳树、杨树、槐树,还有其他的树种,所以槐树不一定最少。故题干说法错误。
【点睛】本题考查统计表的实际应用,通过统计表分析出相应的数据是解题的关键。
16.见详解。
【分析】把购买图书的总数看作单位“1”,科技书和连环画的本数占总数的(1-30%-5%),科技书和连环画的总本数是(320+200)本,根据已知一个数的百分之几是多少,求这个数,先用除法求出总数;再根据求一个数的百分之几是多少,用乘法分别求出故事书的本数、其他书的本数;再根据求一个数是另一个数的百分之几,用除法求出科技书、连环画各占总数的百分之几。据此完成统计图。
【详解】图书的总本数:(320+200)÷(1-30%-5%)
=520÷65%
=520÷0.65
=800(本)
故事书的本数:800×30%=240(本)
其他书的本数:800×5%=40(本)
科技书占总数的分率:320÷800
=0.4
=40%
连环画占总数的分率:200÷800
=0.25
=25%
作图如下:
【点睛】此题考查的目的是理解掌握条形统计图、扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
17.(1)康乃馨;405
(2)25%
【分析】(1)根据扇形统计图,康乃馨的占比最多。将100%减去百合、玫瑰以及其它的百分比,求出康乃馨的百分比。将总的销售额900万元乘康乃馨的百分比,即可求出康乃馨的具体销售额;
(2)将总的销售额看作单位“1”,利用乘法分别求出玫瑰花和百合花的销售额,并利用减法求出两种花的销售额的差。将销售额差除以百合花的销售额,即可求出玫瑰花的销售额比百合花多百分之几。
【详解】(1)900×(100%―20%―25%―10%)
=900×45%
=405(万元)
所以,康乃馨的销售额最多,销售405万元。
(2)900×25%=225(万元)
900×20%=180(万元)
(225―180)÷180
=45÷180
=25%
答:玫瑰花的销售额比百合花多25%。
【点睛】本题考查了扇形统计图的应用,能从扇形统计图中获取信息,并掌握百分数的运算是解题关键。
18.(1)20元
(2)40%
【分析】(1)把李红上周总的消费200元看作单位“1”,买文具的费用占10%。求一个数的百分之几是多少的问题的解法:一个数(单位“1”的量)×百分率=部分量。据此求买文具花的钱可列式为200×10%。
(2)求一个数比另一个数多百分之几的问题的解法:相差的量÷单位“1”的量。先用李红上周总的消费×35%求出餐费的钱数;再用李红上周总的消费×25%求出车费的钱数;最后用(餐费的钱数-车费的钱数)÷车费的钱数,求出李红上周的餐费比车费多百分之几。
【详解】(1)200×10%=20(元)
答:她买文具花了20元。
(2)(200×35%-200×25%)÷(200×25%)
=(70-50)÷50
=20÷50
=40%
答:李红上周的餐费比车费多40%。
【点睛】注意求餐费比车费多百分之几时,不能用35%-25%,因为单位“1”是车费的钱数而不是李红上周的总费用。
19.115.2万平方千米
【分析】把我国国土总面积看作单位“1”,丘陵的面积是96万平方千米,占10%,由此用除法即可求出我们国土总面积,进而把我国国土总面积看作单位“1”,平原占的百分率是12%,求我国平原的面积,根据一个数乘分数的意义,用乘法解答即可。
【详解】96÷10%
=96÷0.1
=960(万平方千米)
960×12%
=960×0.12
=115.2(万平方千米)
答:我国平原的面积是115.2万平方千米。
【点睛】此题是考查如何观察扇形统计图,并从扇形统计图中获取信息,然后再根据所获取的信息解决实际问题。
20.1200元
【分析】淘气家这个月的总支出额看作单位“1”,根据已知一个数的百分之几是多少,求这个数,用除法求出总支出,再根据求一个数的百分之几是多少,用乘法解答。
【详解】200÷(25%-20%)×30%
=200÷0.05×0.3
=4000×0.3
=1200(元)
答:淘气家这个月的教育支出是1200元。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
21.(1)见详解;(2)0.2千米;(3)10分钟
【分析】(1)观察折线统计图可知,骑自行车的时间是8分钟,参观活动的时间是(30-8)分钟,明显参观活动时间大于骑自行车时间,所以扇形统计图上面的括号填①,下面的括号填②;
(2)观察题意可知,多多骑自行车骑了(3-1.4)千米,根据速度=路程÷时间,用(3-1.4)÷8即可求出多多骑自行车平均每分钟多少千米;
(3)把多多所花的总时间看作单位“1”,观察扇形统计图可知,乘公交车回家的时间占总时间的,则骑自行车的时间和参观活动的时间一共占总时间的(1-),根据分数除法的意义,用30÷(1-)即可求出总时间,然后用总时间减去30分钟,即可求出乘公交车回家的时间。
【详解】(1)30-8=22(分钟)
22>8
扇形统计图如下:
(2)(3-1.4)÷8
=1.6÷8
=0.2(千米)
答:多多骑自行车平均每分钟0.2千米。
(3)30÷(1-)
=30÷
=30×
=40(分钟)
40-30=10(分钟)
答:多多从博物馆坐公交车回家,用了10分钟。
【点睛】此题考查的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
22.(1)扇形;5
(2)2400
(3)图形见详解
(4)2280
【分析】(1)根据统计图的特点,可知图(1)是扇形统计图,把调查的总人数看作单位“1”,根据减法的意义,用减法解答。
(2)把调查的总人数看作单位“1”,根据已知一个数的百分之几是多少,求这个数,用除法解答。
(3)根据求一个数的百分之几是多少,用乘法分别求出B、C的人数,据此完成条形统计图。
(4)根据减法的意义,用调查的总人数减去C的人数就是不会乱扔垃圾的人数。
【详解】(1)1-50%-45%
=50%-45%
=5%
则图(1)是扇形统计图,处理方式为C的占调查总人数的5%。
(2)1200÷50%
=1200÷05
=2400(人)
则环保组织在某社区一共调查了2400人。
(3)2400×45%=1080(人)
2400×5%=120(人)
作图如下:
(4)2400-120=2280(人)
则不会乱扔垃圾的一共有2280人。
【点睛】此题考查目的是理解掌握扇形统计图、条形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
23.(1)见详解
(2)10;5
(3)见详解
【分析】(1)分别用加法求出甲校、乙校的合计人数,把统计表补充完整;
观察乙校平均每周使用手机时间在30~60分钟人数为50人,占总人数100人的50%,左边的扇形统计图有占50%的扇形,而右边的扇形统计图中没有占比为50%的扇形,由此确定左边的扇形统计图是乙校的,那么右边的扇形统计图就是甲校的;再分别计算出两个学校各个时间段的人数占总人数的百分比,根据扇形面积的大小,把统计图补充完整。
(2)根据求一个数占另一个数的百分之几,用除法解答。
(3)结合自身情况以及统计图表的数据,对六年级学生使用手机提出建议,合理即可。
【详解】(1)甲校合计:10+20+40+20+10=100(人)
乙校合计:20+50+15+10+5=100(人)
甲校:
30分钟及以内占:10÷100×100%=10%
30~60分钟占:20÷100×100%=20%
60~90分钟占:40÷100×100%=40%
90~120分钟占:20÷100×100%=20%
120分钟以上占:10÷100×100%=10%
乙校:
30分钟及以内占:20÷100×100%=20%
30~60分钟占:50÷100×100%=50%
60~90分钟占:15÷100×100%=15%
90~120分钟占:10÷100×100%=10%
120分钟以上占:5÷100×100%=5%
某地区甲、乙两校六年级学生平均每周使用手机时间情况统计表
(2)10÷100×100%=10%
5÷100×100%=5%
在参加调查统计的甲校学生人数中,平均每周使用手机时间在30分钟及以内的人数占10%;
在参加调查统计的乙校学生人数中,平均每周使用手机时间在120分钟以上的人数占5%。
(3)我每周使用手机的时间约是90分钟。建议:不要过度依赖手机,要合理安排使用手机的时间。(答案不唯一)
【点睛】本题考核统计表和扇形统计图的综合应用,根据统计图表提供的信息,解决有关的实际问题。明确求一个数占另一个数的百分之几,用除法计算。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
