2024年江苏省普通高中学业水平合格性考试数学全真模拟试卷02(含解析)
文档属性
| 名称 | 2024年江苏省普通高中学业水平合格性考试数学全真模拟试卷02(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 22:27:05 | ||
图片预览




文档简介
2024年江苏省普通高中学业水平合格性考试
数学全真模拟试卷02
(考试时间:75分钟 满分100分)
一、选择题(本大题共28小题,每小题3分,共84分。每个小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不给分)
1. 集合,集合,则( )
A. B. C. D.
2.某校高一、高二、高三年级分别有学生1100名、1000名、900名,为了了解学生的视力情况,现用分层抽样的方法从中随机抽取容量为60的样本,则应从高二年级抽取的学生人数为( )
A. 18 B. 20 C. 22 D. 24
3.已知,则( )
A. 3 B. 4 C. D. 10
4.某工厂6名工人在一小时内生产零件的个数分别是11,12,13,15,15,18,设该组数据的平均数为a,中位数为b,则( )
A. B.
C. D.
5.已知角终边经过点,则的值为( )
A. B. C. D.
6. 已知非零向量、满足,且,则与的夹角为( )
A. B. C. D.
7.若从甲、乙、丙3位同学中选出2名代表参加学校会议,则甲被选中的概率为( )
A. B. C. D.
8. 已知,,则( )
A. 2 B. C. 4 D.
9. 若,则的最小值为( )
A. B. C. D.
10.已知,则的值为( )
A. B. C. D.
11.下列运算结果中正确的是( )
A. B.
C. D.
12.已知是两个不同平面,直线,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
13.设D为ABC所在平面内一点,,则( )
A. B.
C. D.
14.在中,内角、、所对的边分别为、、,满足,则=( )
A. B. C. D.
15.已知集合,,且有4个子集,则实数的取值范围是( )
A. B.
C. D.
16.若命题:“,使”是真命题,则实数m的取值范围是( )
A. B. C. D.
17.已知,则( )
A. B. C. D.
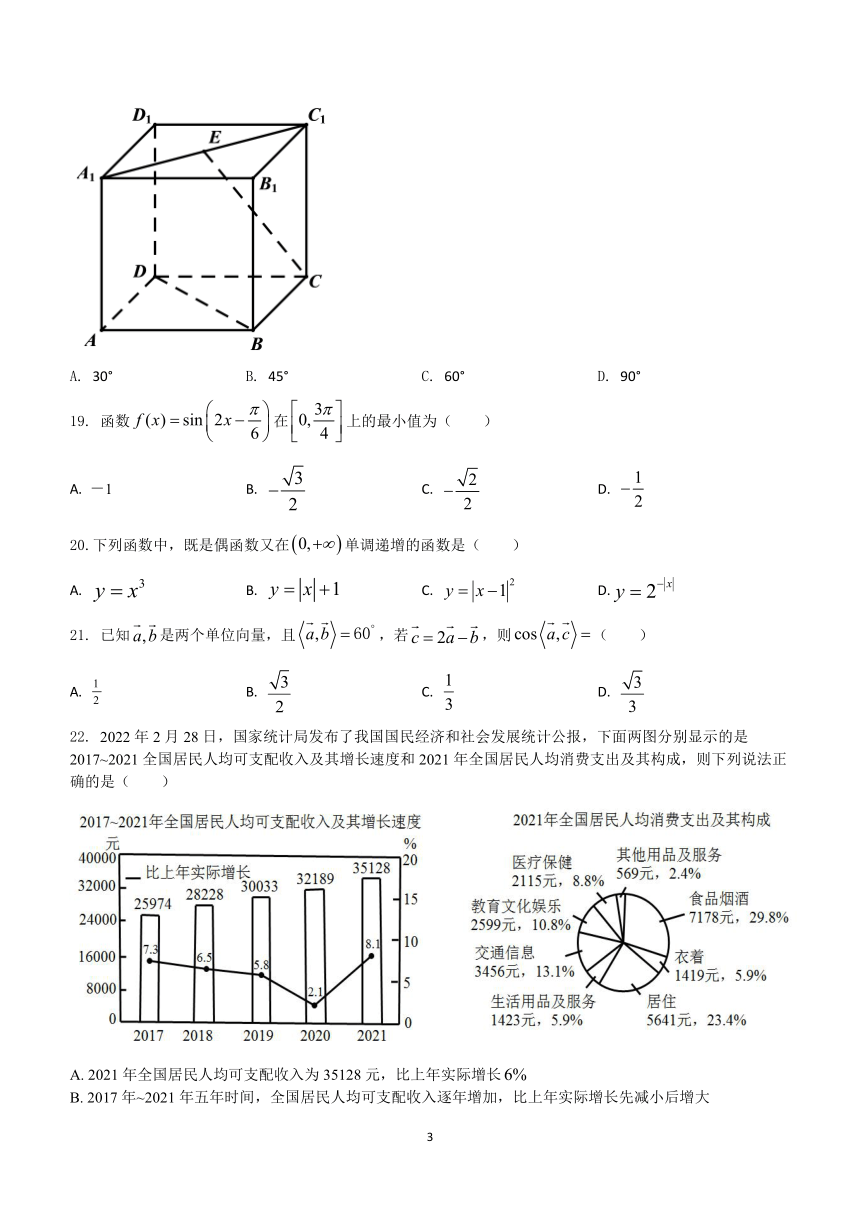
18.如图,在正方体中,为的中点,则异面直线与所成的角为( )
A. 30° B. 45° C. 60° D. 90°
19. 函数在上的最小值为( )
A. -1 B. C. D.
20.下列函数中,既是偶函数又在单调递增的函数是( )
A. B. C. D.
21. 已知是两个单位向量,且,若,则( )
A. B. C. D.
22. 2022年2月28日,国家统计局发布了我国国民经济和社会发展统计公报,下面两图分别显示的是2017~2021全国居民人均可支配收入及其增长速度和2021年全国居民人均消费支出及其构成,则下列说法正确的是( )
A. 2021年全国居民人均可支配收入为35128元,比上年实际增长
B. 2017年~2021年五年时间,全国居民人均可支配收入逐年增加,比上年实际增长先减小后增大
C. 2021年全国居民人均消费支出,食品烟酒和居住占比不足
D. 2021年全国居民人均消费支出,教育文化娱乐占比最小
23.已知m,n是两条不同的直线,,,是三个不同的平面,则下列结论正确的是( ).
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,,则
24.已知向量,满足,,,若,则实数的值为( )
A. 2 B. C. 4 D.
25.已知函数若,则实数( )
A. -5 B. 5 C. -6 D. 6
26.在中,(a,b,c分别为角A,B,C的对边),则的形状为( )
A. 等边三角形 B. 直角三角形
C. 等腰三角形或直角三角形 D. 等腰直角三角形
27.已知,,且,则的最小值为( )
A. 10 B. 9 C. D.
28.已知函数,若,则实数的取值范围是( )
A. B.
C. D.
二、解答题(本大题共2小题,共16分,解答应写出文字说明,证明过程或演算步骤。)
29.(本小题满分8分)如图,在四棱锥中,四边形为矩形,,,分别为,的中点.
(1)求证:平面;
(2)若,求证:平面平面.
30.(本小题满分8分)已知函数.
(1)求的最小值及取得最小值时的取值集合;
(2)若的图象向右平移个单位后得到的函数恰好为偶函数,求的最小值.
2024年江苏省普通高中学业水平合格性考试
数学全真模拟试卷02
(考试时间:75分钟 满分100分)
一、选择题(本大题共28小题,每小题3分,共84分。每个小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不给分)
1. 集合,集合,则( )
A. B. C. D.
【答案】A
【解析】
因为,,
所以.
故选:A
2.某校高一、高二、高三年级分别有学生1100名、1000名、900名,为了了解学生的视力情况,现用分层抽样的方法从中随机抽取容量为60的样本,则应从高二年级抽取的学生人数为( )
A. 18 B. 20 C. 22 D. 24
【答案】B
【解析】根据分层抽样,抽取容量为60的样本时,
应从高二年级抽取的学生人数为(人.
故选:B.
3.已知,则( )
A. 3 B. 4 C. D. 10
【答案】C
【解析】因为,所以.
故选:C.
4.某工厂6名工人在一小时内生产零件的个数分别是11,12,13,15,15,18,设该组数据的平均数为a,中位数为b,则( )
A. B. C. D.
【答案】B
【解析】平均数为,
由这6个数分别是11,12,13,15,15,18,则其中位数为 14.
故选:B.
5.已知角终边经过点,则的值为( )
A. B. C. D.
【答案】D
【解析】因为角终边过点,所以,,,所以,
故选:D.
6. 已知非零向量、满足,且,则与的夹角为( )
A. B. C. D.
【答案】A
【解析】
因为非零向量、满足,且,
则,
所以,,又因为,故.
因此,与的夹角为.
故选:A.
7.若从甲、乙、丙3位同学中选出2名代表参加学校会议,则甲被选中的概率为( )
A. B. C. D.
【答案】C
【解析】根据题意可得从甲、乙、丙3位同学中选出2名代表参加学校会议
(甲,乙),(甲,丙),(乙,丙),基本事件共个,
甲被选中有:(甲,乙),(甲,丙),基本事件共个,
所以甲被选中的概率为: ,
故选:C
8. 已知,,则( )
A. 2 B. C. 4 D.
【答案】C
【解析】由题得=(0,4)
所以.
故选:C
9. 若,则的最小值为( )
A. B. C. D.
【答案】C
【解析】因为,则,
则,
当且仅当时,等号成立,故当时,的最小值为.
故选:C.
10.已知,则的值为( )
A. B. C. D.
【答案】D
【解析】因,
所以,
故选:D
11.下列运算结果中正确的是( )
A. B.
C. D.
【答案】D
【解析】对于A选项,,故A错误;
对于B选项, ,故B错误;
对于C选项,当时,,当时,,故C错误;
对于D选项,,故D正确.
故选:D.
12.已知是两个不同平面,直线,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】由题意,若∥,则∥,
根据面面平行的性质,∥是∥的充分条件;
若∥,根据面面平行的判定定理不能推出∥,故不是充分条件;
∴∥是∥的充分不必要条件,
故选:A.
13.设D为ABC所在平面内一点,,则( )
A. B.
C. D.
【答案】C
【解析】因为,
所以,
故选:C
14.在中,内角、、所对的边分别为、、,满足,则=( )
A. B. C. D.
【答案】D
【解析】在中,
由正弦定理可化成,
,
由余弦定理可得:
,
故选:D.
15.已知集合,,且有4个子集,则实数的取值范围是( )
A. B.
C. D.
【答案】B
【解析】,
因为有4个子集,所以集合中有2个元素,
因为,
所以,且,
所以且,
即实数的取值范围是,
故选:B.
16.若命题:“,使”是真命题,则实数m的取值范围是( )
A. B. C. D.
【答案】C
【解析】∵“,使”是真命题,
∴,解得.
故选:C
17.已知,则( )
A. B. C. D.
【答案】C
【解析】因为,
整理可得,解得,
所以,.
故选:C.
18.如图,在正方体中,为的中点,则异面直线与所成的角为( )
A. 30° B. 45° C. 60° D. 90°
【答案】D
【解析】连接,则,
因为平面,在平面内,
所以,
因为,
所以平面,
因为在平面内,
所以,
所以异面直线与所成的角为,
故选:D
19. 函数在上的最小值为( )
A. -1 B. C. D.
【答案】B
【解析】当时,,
则当时,,
故选:B.
20.下列函数中,既是偶函数又在单调递增的函数是( )
A. B. C. D.
【答案】B
【解析】对于A中,函数为奇函数,不符合题意;
对于B中,函数的定义域为,且,所以为偶函数,
当时,函数为单调递增函数,符合题意;
对于C中,函数非奇非偶函数,不符合题意;
对于D中,当时,函数单调递减函数,不符合题意.
故选:B.
21. 已知是两个单位向量,且,若,则( )
A. B. C. D.
【答案】B
【解析】已知是两个单位向量,,
若,则,
,
故.
故选:B
22. 2022年2月28日,国家统计局发布了我国国民经济和社会发展统计公报,下面两图分别显示的是2017~2021全国居民人均可支配收入及其增长速度和2021年全国居民人均消费支出及其构成,则下列说法正确的是( )
A. 2021年全国居民人均可支配收入为35128元,比上年实际增长
B. 2017年~2021年五年时间,全国居民人均可支配收入逐年增加,比上年实际增长先减小后增大
C. 2021年全国居民人均消费支出,食品烟酒和居住占比不足
D. 2021年全国居民人均消费支出,教育文化娱乐占比最小
【答案】B
【解析】对于A,2021年全国居民人均可支配收入为35128元,2020年全国居民人均可支配收入为32189元,所以2021年比2020年增长,所以A错误,
对于B,由统计图可知2018全国居民人均可支配收入比2017增长,
2019全国居民人均可支配收入比2018增长,
2020全国居民人均可支配收入比2019增长,
2021全国居民人均可支配收入比2020增长,
所以2017年~2021年五年时间,全国居民人均可支配收入逐年增加,比上年实际增长先减小后增大,所以B正确,
对于C,2021年全国居民人均消费支出,食品烟酒和居住占比为,所以C错误,
对于D,由右图可知,2021年全国居民人均消费支出,其他用品及服务占比最小,为,所以D错误,
故选:B
23.已知m,n是两条不同的直线,,,是三个不同的平面,则下列结论正确的是( ).
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,,则
【答案】D
【解析】A:,,则或,错误;
B:,,则或,错误;
C:,,则相交或平行,错误;
D:,,则,又,故,正确.
故选:D
24.已知向量,满足,,,若,则实数的值为( )
A. 2 B. C. 4 D.
【答案】C
【解析】因为,所以,
依题意,则,
故选:C.
25.已知函数若,则实数( )
A. -5 B. 5 C. -6 D. 6
【答案】A
【解析】由题意可得,
因为,即,
所以,得,
故选:A
26.在中,(a,b,c分别为角A,B,C的对边),则的形状为( )
A. 等边三角形 B. 直角三角形
C. 等腰三角形或直角三角形 D. 等腰直角三角形
【答案】B
【解析】∵,∴,,,整理得,∴三角形为直角三角形.
故选:B.
27.已知,,且,则的最小值为( )
A. 10 B. 9 C. D.
【答案】C
【解析】由已知,令,,
所以,,代入得:,
因为,,
所以
.
当且仅当时,即时等号成立.
的最小值为.
故选:C.
28.已知函数,若,则实数的取值范围是( )
A. B.
C. D.
【答案】B
【解析】∵,均为奇函数,且为R上的增函数,
∴函数为奇函数,在R上为增函数,
由,可得,
∴,即,
∴,
故选:B
二、解答题(本大题共2小题,共16分,解答应写出文字说明,证明过程或演算步骤。)
29.(本小题满分8分)如图,在四棱锥中,四边形为矩形,,,分别为,的中点.
(1)求证:平面;
(2)若,求证:平面平面.
【答案】(1)证明见解析;(2)证明见解析.
【解析】(1)连结,
由已知,为和的中点,
又为的中点,.
平面,平面,平面.
(2),,,平面.
平面,.
,,平面.
平面,∴平面平面.
30.(本小题满分8分)已知函数.
(1)求的最小值及取得最小值时的取值集合;
(2)若的图象向右平移个单位后得到的函数恰好为偶函数,求的最小值.
【答案】(1)最小值为-2,此时
(2).
【解析】(1)因为,
所以当即时,取得最小值-2,
所以的最小值为-2,此时x的取值集合为;
(2)设的图象向右平移个单位后得到函数,
则,
因为为偶函数,所以,
即, 展开可得,
所以恒成立,所以,
所以,
又因为,所以.
数学全真模拟试卷02
(考试时间:75分钟 满分100分)
一、选择题(本大题共28小题,每小题3分,共84分。每个小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不给分)
1. 集合,集合,则( )
A. B. C. D.
2.某校高一、高二、高三年级分别有学生1100名、1000名、900名,为了了解学生的视力情况,现用分层抽样的方法从中随机抽取容量为60的样本,则应从高二年级抽取的学生人数为( )
A. 18 B. 20 C. 22 D. 24
3.已知,则( )
A. 3 B. 4 C. D. 10
4.某工厂6名工人在一小时内生产零件的个数分别是11,12,13,15,15,18,设该组数据的平均数为a,中位数为b,则( )
A. B.
C. D.
5.已知角终边经过点,则的值为( )
A. B. C. D.
6. 已知非零向量、满足,且,则与的夹角为( )
A. B. C. D.
7.若从甲、乙、丙3位同学中选出2名代表参加学校会议,则甲被选中的概率为( )
A. B. C. D.
8. 已知,,则( )
A. 2 B. C. 4 D.
9. 若,则的最小值为( )
A. B. C. D.
10.已知,则的值为( )
A. B. C. D.
11.下列运算结果中正确的是( )
A. B.
C. D.
12.已知是两个不同平面,直线,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
13.设D为ABC所在平面内一点,,则( )
A. B.
C. D.
14.在中,内角、、所对的边分别为、、,满足,则=( )
A. B. C. D.
15.已知集合,,且有4个子集,则实数的取值范围是( )
A. B.
C. D.
16.若命题:“,使”是真命题,则实数m的取值范围是( )
A. B. C. D.
17.已知,则( )
A. B. C. D.
18.如图,在正方体中,为的中点,则异面直线与所成的角为( )
A. 30° B. 45° C. 60° D. 90°
19. 函数在上的最小值为( )
A. -1 B. C. D.
20.下列函数中,既是偶函数又在单调递增的函数是( )
A. B. C. D.
21. 已知是两个单位向量,且,若,则( )
A. B. C. D.
22. 2022年2月28日,国家统计局发布了我国国民经济和社会发展统计公报,下面两图分别显示的是2017~2021全国居民人均可支配收入及其增长速度和2021年全国居民人均消费支出及其构成,则下列说法正确的是( )
A. 2021年全国居民人均可支配收入为35128元,比上年实际增长
B. 2017年~2021年五年时间,全国居民人均可支配收入逐年增加,比上年实际增长先减小后增大
C. 2021年全国居民人均消费支出,食品烟酒和居住占比不足
D. 2021年全国居民人均消费支出,教育文化娱乐占比最小
23.已知m,n是两条不同的直线,,,是三个不同的平面,则下列结论正确的是( ).
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,,则
24.已知向量,满足,,,若,则实数的值为( )
A. 2 B. C. 4 D.
25.已知函数若,则实数( )
A. -5 B. 5 C. -6 D. 6
26.在中,(a,b,c分别为角A,B,C的对边),则的形状为( )
A. 等边三角形 B. 直角三角形
C. 等腰三角形或直角三角形 D. 等腰直角三角形
27.已知,,且,则的最小值为( )
A. 10 B. 9 C. D.
28.已知函数,若,则实数的取值范围是( )
A. B.
C. D.
二、解答题(本大题共2小题,共16分,解答应写出文字说明,证明过程或演算步骤。)
29.(本小题满分8分)如图,在四棱锥中,四边形为矩形,,,分别为,的中点.
(1)求证:平面;
(2)若,求证:平面平面.
30.(本小题满分8分)已知函数.
(1)求的最小值及取得最小值时的取值集合;
(2)若的图象向右平移个单位后得到的函数恰好为偶函数,求的最小值.
2024年江苏省普通高中学业水平合格性考试
数学全真模拟试卷02
(考试时间:75分钟 满分100分)
一、选择题(本大题共28小题,每小题3分,共84分。每个小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不给分)
1. 集合,集合,则( )
A. B. C. D.
【答案】A
【解析】
因为,,
所以.
故选:A
2.某校高一、高二、高三年级分别有学生1100名、1000名、900名,为了了解学生的视力情况,现用分层抽样的方法从中随机抽取容量为60的样本,则应从高二年级抽取的学生人数为( )
A. 18 B. 20 C. 22 D. 24
【答案】B
【解析】根据分层抽样,抽取容量为60的样本时,
应从高二年级抽取的学生人数为(人.
故选:B.
3.已知,则( )
A. 3 B. 4 C. D. 10
【答案】C
【解析】因为,所以.
故选:C.
4.某工厂6名工人在一小时内生产零件的个数分别是11,12,13,15,15,18,设该组数据的平均数为a,中位数为b,则( )
A. B. C. D.
【答案】B
【解析】平均数为,
由这6个数分别是11,12,13,15,15,18,则其中位数为 14.
故选:B.
5.已知角终边经过点,则的值为( )
A. B. C. D.
【答案】D
【解析】因为角终边过点,所以,,,所以,
故选:D.
6. 已知非零向量、满足,且,则与的夹角为( )
A. B. C. D.
【答案】A
【解析】
因为非零向量、满足,且,
则,
所以,,又因为,故.
因此,与的夹角为.
故选:A.
7.若从甲、乙、丙3位同学中选出2名代表参加学校会议,则甲被选中的概率为( )
A. B. C. D.
【答案】C
【解析】根据题意可得从甲、乙、丙3位同学中选出2名代表参加学校会议
(甲,乙),(甲,丙),(乙,丙),基本事件共个,
甲被选中有:(甲,乙),(甲,丙),基本事件共个,
所以甲被选中的概率为: ,
故选:C
8. 已知,,则( )
A. 2 B. C. 4 D.
【答案】C
【解析】由题得=(0,4)
所以.
故选:C
9. 若,则的最小值为( )
A. B. C. D.
【答案】C
【解析】因为,则,
则,
当且仅当时,等号成立,故当时,的最小值为.
故选:C.
10.已知,则的值为( )
A. B. C. D.
【答案】D
【解析】因,
所以,
故选:D
11.下列运算结果中正确的是( )
A. B.
C. D.
【答案】D
【解析】对于A选项,,故A错误;
对于B选项, ,故B错误;
对于C选项,当时,,当时,,故C错误;
对于D选项,,故D正确.
故选:D.
12.已知是两个不同平面,直线,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】由题意,若∥,则∥,
根据面面平行的性质,∥是∥的充分条件;
若∥,根据面面平行的判定定理不能推出∥,故不是充分条件;
∴∥是∥的充分不必要条件,
故选:A.
13.设D为ABC所在平面内一点,,则( )
A. B.
C. D.
【答案】C
【解析】因为,
所以,
故选:C
14.在中,内角、、所对的边分别为、、,满足,则=( )
A. B. C. D.
【答案】D
【解析】在中,
由正弦定理可化成,
,
由余弦定理可得:
,
故选:D.
15.已知集合,,且有4个子集,则实数的取值范围是( )
A. B.
C. D.
【答案】B
【解析】,
因为有4个子集,所以集合中有2个元素,
因为,
所以,且,
所以且,
即实数的取值范围是,
故选:B.
16.若命题:“,使”是真命题,则实数m的取值范围是( )
A. B. C. D.
【答案】C
【解析】∵“,使”是真命题,
∴,解得.
故选:C
17.已知,则( )
A. B. C. D.
【答案】C
【解析】因为,
整理可得,解得,
所以,.
故选:C.
18.如图,在正方体中,为的中点,则异面直线与所成的角为( )
A. 30° B. 45° C. 60° D. 90°
【答案】D
【解析】连接,则,
因为平面,在平面内,
所以,
因为,
所以平面,
因为在平面内,
所以,
所以异面直线与所成的角为,
故选:D
19. 函数在上的最小值为( )
A. -1 B. C. D.
【答案】B
【解析】当时,,
则当时,,
故选:B.
20.下列函数中,既是偶函数又在单调递增的函数是( )
A. B. C. D.
【答案】B
【解析】对于A中,函数为奇函数,不符合题意;
对于B中,函数的定义域为,且,所以为偶函数,
当时,函数为单调递增函数,符合题意;
对于C中,函数非奇非偶函数,不符合题意;
对于D中,当时,函数单调递减函数,不符合题意.
故选:B.
21. 已知是两个单位向量,且,若,则( )
A. B. C. D.
【答案】B
【解析】已知是两个单位向量,,
若,则,
,
故.
故选:B
22. 2022年2月28日,国家统计局发布了我国国民经济和社会发展统计公报,下面两图分别显示的是2017~2021全国居民人均可支配收入及其增长速度和2021年全国居民人均消费支出及其构成,则下列说法正确的是( )
A. 2021年全国居民人均可支配收入为35128元,比上年实际增长
B. 2017年~2021年五年时间,全国居民人均可支配收入逐年增加,比上年实际增长先减小后增大
C. 2021年全国居民人均消费支出,食品烟酒和居住占比不足
D. 2021年全国居民人均消费支出,教育文化娱乐占比最小
【答案】B
【解析】对于A,2021年全国居民人均可支配收入为35128元,2020年全国居民人均可支配收入为32189元,所以2021年比2020年增长,所以A错误,
对于B,由统计图可知2018全国居民人均可支配收入比2017增长,
2019全国居民人均可支配收入比2018增长,
2020全国居民人均可支配收入比2019增长,
2021全国居民人均可支配收入比2020增长,
所以2017年~2021年五年时间,全国居民人均可支配收入逐年增加,比上年实际增长先减小后增大,所以B正确,
对于C,2021年全国居民人均消费支出,食品烟酒和居住占比为,所以C错误,
对于D,由右图可知,2021年全国居民人均消费支出,其他用品及服务占比最小,为,所以D错误,
故选:B
23.已知m,n是两条不同的直线,,,是三个不同的平面,则下列结论正确的是( ).
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,,则
【答案】D
【解析】A:,,则或,错误;
B:,,则或,错误;
C:,,则相交或平行,错误;
D:,,则,又,故,正确.
故选:D
24.已知向量,满足,,,若,则实数的值为( )
A. 2 B. C. 4 D.
【答案】C
【解析】因为,所以,
依题意,则,
故选:C.
25.已知函数若,则实数( )
A. -5 B. 5 C. -6 D. 6
【答案】A
【解析】由题意可得,
因为,即,
所以,得,
故选:A
26.在中,(a,b,c分别为角A,B,C的对边),则的形状为( )
A. 等边三角形 B. 直角三角形
C. 等腰三角形或直角三角形 D. 等腰直角三角形
【答案】B
【解析】∵,∴,,,整理得,∴三角形为直角三角形.
故选:B.
27.已知,,且,则的最小值为( )
A. 10 B. 9 C. D.
【答案】C
【解析】由已知,令,,
所以,,代入得:,
因为,,
所以
.
当且仅当时,即时等号成立.
的最小值为.
故选:C.
28.已知函数,若,则实数的取值范围是( )
A. B.
C. D.
【答案】B
【解析】∵,均为奇函数,且为R上的增函数,
∴函数为奇函数,在R上为增函数,
由,可得,
∴,即,
∴,
故选:B
二、解答题(本大题共2小题,共16分,解答应写出文字说明,证明过程或演算步骤。)
29.(本小题满分8分)如图,在四棱锥中,四边形为矩形,,,分别为,的中点.
(1)求证:平面;
(2)若,求证:平面平面.
【答案】(1)证明见解析;(2)证明见解析.
【解析】(1)连结,
由已知,为和的中点,
又为的中点,.
平面,平面,平面.
(2),,,平面.
平面,.
,,平面.
平面,∴平面平面.
30.(本小题满分8分)已知函数.
(1)求的最小值及取得最小值时的取值集合;
(2)若的图象向右平移个单位后得到的函数恰好为偶函数,求的最小值.
【答案】(1)最小值为-2,此时
(2).
【解析】(1)因为,
所以当即时,取得最小值-2,
所以的最小值为-2,此时x的取值集合为;
(2)设的图象向右平移个单位后得到函数,
则,
因为为偶函数,所以,
即, 展开可得,
所以恒成立,所以,
所以,
又因为,所以.
同课章节目录
