2024年江苏省普通高中学业水平合格性考试数学全真模拟试卷01(含解析)
文档属性
| 名称 | 2024年江苏省普通高中学业水平合格性考试数学全真模拟试卷01(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 22:27:44 | ||
图片预览




文档简介
2024年江苏省普通高中学业水平合格性考试
数学全真模拟试卷01
(考试时间:75分钟 满分100分)
一、选择题(本大题共28小题,每小题3分,共84分。每个小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不给分)
1.设集合,,则( )
A. B. C. D.
2. 若命题:,则命题的否定为( )
A. B.
C. D.
3. 设a,b,c∈R,其中正确的是( )
A. 若,则 B. 若, 则
C. 若,则 D. 若,则
4.若角的终边经过点,则( )
A. B. C. D.
5.某部门为了了解一批树苗的生长情况,在3000棵树苗中随机抽取200棵,统计这200棵树苗的高度,并绘制了频率分布直方图(如图),那么根据该图可推测,在这3000棵树苗中高度小于的树苗棵数是( ).
A. 360 B. 600 C. 840 D. 1320
6.一只不透明的盒子中装有形状、大小相同的4只球,其中有2只白球,2只黑球,若从中随机摸出两只球,则它们颜色不同的概率是( )
A. B. C. D.
7. 函数的定义域是( )
A. B.
C. D.
8. 如图,已知向量,那么下列结论正确的是( )
B.
C. D.
9. 在中,已知,,,则( )
A. B. C. D.
10.复数在复平面内对应的点在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
11.幂函数为偶函数,且在上为减函数的是( )
A. B.
C. D.
12.抛掷两枚质地均匀的硬币,设事件“第一枚硬币正面向上”,设事件“第二枚硬币正面向上”,则( )
A. 事件与互为对立事件 B. 件与为互斥事件
C. 事件与事件相等 D. 事件与相互独立
13. 运动员甲10次射击成绩(单位:环)如下:7,8,9,7,4,8,9,9,7,2,则下列关于这组数据说法不正确的是( ).
A. 众数为7和9 B. 平均数为7
C. 中位数为7 D. 方差为
14.已知m,n表示两条不同直线,表示平面,下列说法正确的是
A. 若则 B. 若,,则
C. 若,,则 D. 若,,则
16.某工厂生产甲、乙、丙三种型号的产品,产品数量之比为3:5:7,现用分层抽样的方法抽出容量为n的样本,其中甲种产品有18件,则样本容量n=( )
A. 45 B. 54 C. 90 D. 126
17. 将函数的图象向右平移个长度单位,再将所得图象上所有点的横坐标变为原来的2倍(纵坐标不变),得到函数的图象,则的解析式为( )
A. B.
C. D.
18.关于x的不等式的解集为,则实数a的值为( )
A. B. C. D. 4
19. 知两点,与平行,且方向相反的向量可能是( )
A. B.
C. D.
20. 已知函数在上单调递减,则实数的取值范围是( )
A. B. C. D.
21. 已知,则( )
A. B. C. 3 D.
22.在长方体中,点E为的中点,,且,则异面直线AE与BC所成角的余弦值为( )
A. B. C. D.
23.已知是定义在上的偶函数,当时,,则时,( )
A. B.
C. D.
24.设,,,则( )
A. B. C. D.
25.在,其内角的对边分别为,若,则的形状是( )
A. 等腰三角形 B. 直角三角形
C. 等腰直角三角形 D. 等腰或直角三角形
26.已知平面,直线m,n.( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
27.党的二十大报告指出,“坚持精准治污、科学治污、依法治污,持续深入打好蓝天、碧水、净土保卫战.加强污染物协同控制,基本消除重污染天气.”按照相关规定,某化工厂产生的废气中的某类污染物经过过滤装置的处理,含量降至过滤前的以下才能排放.已知过滤过程中,废气中污染物的含量(单位:mg/L)与时间(单位:min)的关系为,其中,是常数.若时,该类污染物的含量降为过滤前的,那么废气至少需要过滤( )才能排放(结果保留整数,参考数据:).
A. 7 B. 8 C. 9 D. 10
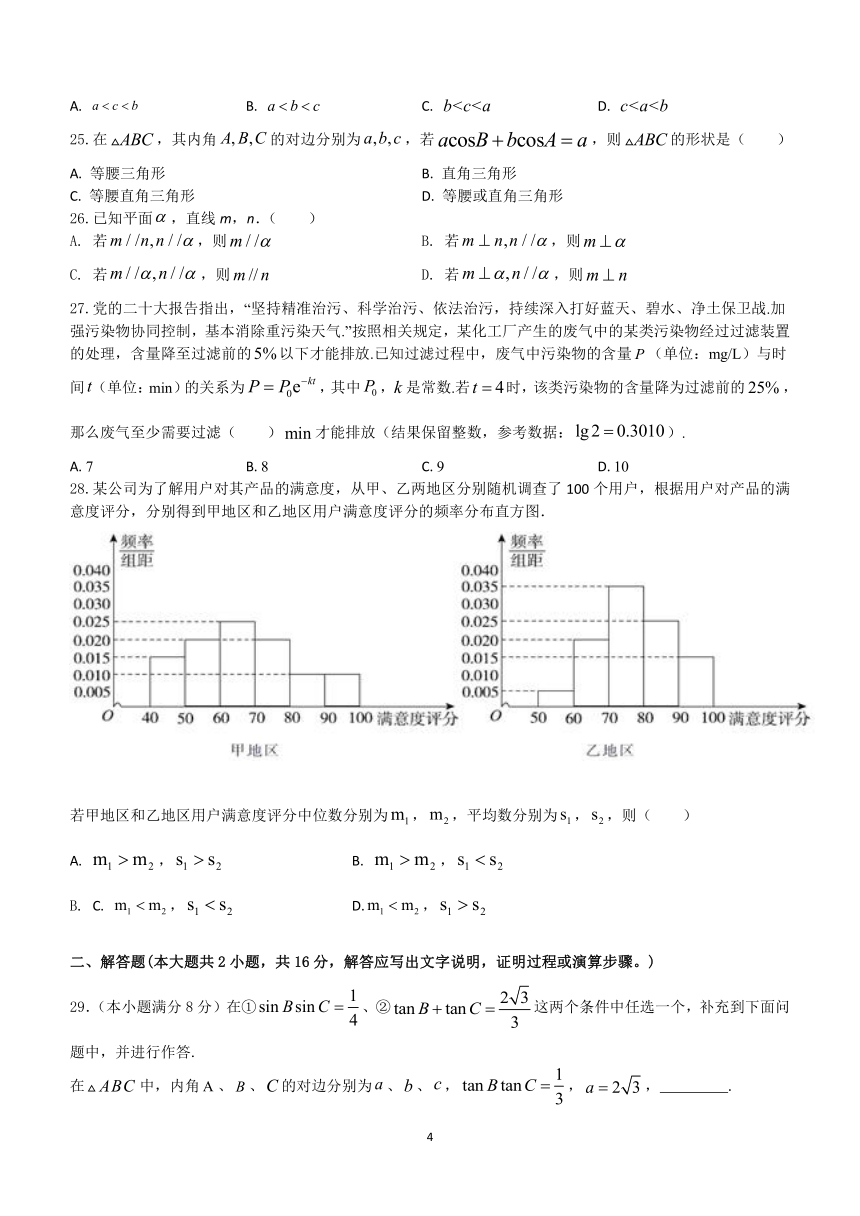
28.某公司为了解用户对其产品的满意度,从甲、乙两地区分别随机调查了100个用户,根据用户对产品的满意度评分,分别得到甲地区和乙地区用户满意度评分的频率分布直方图.
若甲地区和乙地区用户满意度评分中位数分别为,,平均数分别为,,则( )
, B. ,
C. , D.,
二、解答题(本大题共2小题,共16分,解答应写出文字说明,证明过程或演算步骤。)
29.(本小题满分8分)在①、②这两个条件中任选一个,补充到下面问题中,并进行作答.
在中,内角、、的对边分别为、、,,, .
(1)求角、、的大小;
(2)求的周长和面积.
30.(本小题满分8分)如图,四棱柱的底面是正方形,侧面是菱形,,平面平面,E,F分别为的中点.
(1)求证:平面;
(2)求与平面所成角的正切值.
024年江苏省普通高中学业水平合格性考试
数学全真模拟试卷01
(考试时间:75分钟 满分100分)
一、选择题(本大题共28小题,每小题3分,共84分。每个小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不给分)
1.设集合,,则( )
A. B. C. D.
【答案】B
【解析】由题设有,
故选:B
2. 若命题:,则命题的否定为( )
A. B.
C. D.
【答案】D
【解析】根据存在量词的否定是全称量词可得命题的否定为.
故选:D
3. 设a,b,c∈R,其中正确的是( )
A. 若,则 B. 若, 则
C. 若,则 D. 若,则
【答案】A
【解析】当时,BD都不正确,当时C错误,由不等式的基本性质得A正确;
故选:A
4.若角的终边经过点,则( )
A. B. C. D.
【答案】A
【解析】点到原点的距离为,所以,
故选:A.
5.某部门为了了解一批树苗的生长情况,在3000棵树苗中随机抽取200棵,统计这200棵树苗的高度,并绘制了频率分布直方图(如图),那么根据该图可推测,在这3000棵树苗中高度小于的树苗棵数是( ).
A. 360 B. 600 C. 840 D. 1320
【答案】B
【解析】由频率分布直方图可得,小于的树苗的频率,所以可推测,3000棵树苗中高度小于的树苗棵数
故选:B
6.一只不透明的盒子中装有形状、大小相同的4只球,其中有2只白球,2只黑球,若从中随机摸出两只球,则它们颜色不同的概率是( )
A. B. C. D.
【答案】B
【解析】设从中随机摸出两只球,它们颜色不同为事件A,
∵基本事件总数为6,
事件A中包含的基本事件数为4,
∴P(A)==.
故选:B.
7. 函数的定义域是( )
A. B.
C. D.
【答案】D
【解析】的定义域满足,解得.
故选:D
8. 如图,已知向量,那么下列结论正确的是( )
A. B. C. D.
【答案】B
【解析】根据向量加法的三角形法则,向量首尾顺次相连,所以根据图形可知,与向量反向且相等,所以.
故选:B.
9. 在中,已知,,,则( )
A. B. C. D.
【答案】A
【解析】在中,已知,,,
由余弦定理得:,
故选:A
10.复数在复平面内对应的点在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
【答案】D
【解析】,故对应的点为
故选:D.
11.幂函数为偶函数,且在上为减函数的是( )
A. B.
C. D.
【答案】A
【解析】对A:,则,
故偶函数,且在上为减函数,A正确;
对B:的定义域为,即定义域不关于原点对称,故为非奇非偶函数,B错误;
对C:,
故为偶函数,且在上为增函数,C正确;
对D:,故为奇函数,D错误.
故选:A.
12.抛掷两枚质地均匀的硬币,设事件“第一枚硬币正面向上”,设事件“第二枚硬币正面向上”,则( )
A. 事件与互为对立事件 B. 件与为互斥事件
C. 事件与事件相等 D. 事件与相互独立
【答案】D
【解析】抛掷两枚质地均匀的硬币,
设事件 “第一枚硬币正面向上”,
设事件 “第二枚硬币正面向上”,
事件发生与否与事件无关,事件发生与否与事件无关,
事件与事件相互独立.
故选:D.
13. 运动员甲10次射击成绩(单位:环)如下:7,8,9,7,4,8,9,9,7,2,则下列关于这组数据说法不正确的是( ).
A. 众数为7和9 B. 平均数为7
C. 中位数为7 D. 方差为
【答案】C
【解析】由题意,这组数据中7和9都出现3次,其余数出现次数没超过3次,
故众数为7和9,A正确;
计算平均数为 ,故B正确;
将10次射击成绩从小到大排列为:2,4,7, 7, 7,8,8,9,9,9,
则中位数为 ,故C错误;
方差为,
故D正确,
故选:C
14.已知m,n表示两条不同直线,表示平面,下列说法正确的是
A. 若则 B. 若,,则
C. 若,,则 D. 若,,则
【答案】B
【解析】
线面垂直,则有该直线和平面内所有的直线都垂直,故B正确.
故选:B
15.函数的定义域为( )
A. B.
C. D.
【答案】B
【解析】由有意义,则,
该不等式等价于,解得.
故选:B.
16.某工厂生产甲、乙、丙三种型号的产品,产品数量之比为3:5:7,现用分层抽样的方法抽出容量为n的样本,其中甲种产品有18件,则样本容量n=( )
A. 45 B. 54 C. 90 D. 126
【答案】C
【解析】A种型号产品所占的比例为,
,故样本容量n=90.
故选C.
17. 将函数的图象向右平移个长度单位,再将所得图象上所有点的横坐标变为原来的2倍(纵坐标不变),得到函数的图象,则的解析式为( )
A. B.
C. D.
【答案】D
【解析】函数的图象向右平移个长度单位得到,
再将所得图象上所有点的横坐标变为原来的2倍(纵坐标不变)得到
.
故选:D
18.关于x的不等式的解集为,则实数a的值为( )
A. B. C. D. 4
【答案】D
【解析】由且不等于1,
由题意得,,解得.
故选:D.
19. 知两点,与平行,且方向相反的向量可能是( )
A. B.
C. D.
【答案】A
【解析】,
A选项, ,故满足题意
B、C、D选项中的不与平行
故选:A
20. 已知函数在上单调递减,则实数的取值范围是( )
A. B. C. D.
【答案】D
【解析】由题意知函数在上单调递减,
而图象开口向上,对称轴为,则,
即实数的取值范围是,
故选:D
21. 已知,则( )
A. B. C. 3 D.
【答案】A
【解析】.
故选:A.
22.在长方体中,点E为的中点,,且,则异面直线AE与BC所成角的余弦值为( )
A. B. C. D.
【答案】C
【解析】
连接,由可得或其补角即为异面直线AE与BC所成角,又面,面,则,
则,同理可得,,则,,
则异面直线AE与BC所成角的余弦值为.
故选:C.
23.已知是定义在上的偶函数,当时,,则时,( )
A. B.
C. D.
【答案】A
【解析】当时,,则 ①
又因为是定义在上的偶函数,
所以 ②
所以由①②得:当时,.
故选:A.
24.设,,,则( )
A. B. C. D.
【答案】C
【解析】∵,
又,
∴.
故选:C.
25.在,其内角的对边分别为,若,则的形状是( )
A. 等腰三角形 B. 直角三角形
C. 等腰直角三角形 D. 等腰或直角三角形
【答案】A
【解析】因为在,,
所以,
又,
所以,,
所以为等腰三角形.
故选:A.
26.已知平面,直线m,n.( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
【答案】D
【解析】对A,若,则或,故A错误;
对B,若,则和平行、相交或在平面内,故B错误;
对C,若,则平行、相交或异面,故C错误;
对D,若,则,故D正确.
故选:D.
27.党的二十大报告指出,“坚持精准治污、科学治污、依法治污,持续深入打好蓝天、碧水、净土保卫战.加强污染物协同控制,基本消除重污染天气.”按照相关规定,某化工厂产生的废气中的某类污染物经过过滤装置的处理,含量降至过滤前的以下才能排放.已知过滤过程中,废气中污染物的含量(单位:mg/L)与时间(单位:min)的关系为,其中,是常数.若时,该类污染物的含量降为过滤前的,那么废气至少需要过滤( )才能排放(结果保留整数,参考数据:).
A. 7 B. 8 C. 9 D. 10
【答案】C
【解析】依题意可得,所以,两边取对数可得,
所以,则,
所以,令,即,所以,
即,
所以,
所以废气至少需要过滤才能排放.
故选:C
28.某公司为了解用户对其产品的满意度,从甲、乙两地区分别随机调查了100个用户,根据用户对产品的满意度评分,分别得到甲地区和乙地区用户满意度评分的频率分布直方图.
若甲地区和乙地区用户满意度评分中位数分别为,,平均数分别为,,则( )
A. , B. , C. , D. ,
【答案】C
【解析】由频率分布直方图得:
甲地区,的频率为:,
,的频率为,
甲地区用户满意度评分的中位数,
甲地区的平均数.
乙地区,的频率为:,
,的频率为:,
乙地区用户满意度评分的中位数,
乙地区的平均数.
,.
故选:C.
二、解答题(本大题共2小题,共16分,解答应写出文字说明,证明过程或演算步骤。)
29.(本小题满分8分)在①、②这两个条件中任选一个,补充到下面问题中,并进行作答.
在中,内角、、的对边分别为、、,,, .
(1)求角、、的大小;
(2)求的周长和面积.
【答案】(1),,;(2)周长为,面积为.
【解析】选①:
(1)因为,,所以,
则,
因为,所以,,
因为,
所以,.
(2)因为,,,,
所以,的周长为,
的面积.
选②:
(1)联立,解得,
因为,,所以,.
(2)因为,,,,
所以,周长为,
的面积.
30.(本小题满分8分)如图,四棱柱的底面是正方形,侧面是菱形,,平面平面,E,F分别为的中点.
(1)求证:平面;
(2)求与平面所成角的正切值.
【答案】(1)证明见解析;(2).
【解析】(1)设中点为G,连接,
因为E,G分别为的中点,
所以,
在正方形中,F是的中点,
所以,且,
所以且,
所以四边形是平行四边形,
所以,
因为平面平面,
所以平面.
(2)过作于M,过E作于H,连接,则,
因为平面平面,且平面平面,
平面,所以平面,
所以是在平面内的射影,
所以为直线与平面所成的角,
设正方形的边长为a,
因为侧面是菱形,,所以,
又因为且E是的中点,所以,
在正方形中,F为中点,H为的四等分点,,
所以在直角三角形中,,
所以与平面所成角的正切值为.
数学全真模拟试卷01
(考试时间:75分钟 满分100分)
一、选择题(本大题共28小题,每小题3分,共84分。每个小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不给分)
1.设集合,,则( )
A. B. C. D.
2. 若命题:,则命题的否定为( )
A. B.
C. D.
3. 设a,b,c∈R,其中正确的是( )
A. 若,则 B. 若, 则
C. 若,则 D. 若,则
4.若角的终边经过点,则( )
A. B. C. D.
5.某部门为了了解一批树苗的生长情况,在3000棵树苗中随机抽取200棵,统计这200棵树苗的高度,并绘制了频率分布直方图(如图),那么根据该图可推测,在这3000棵树苗中高度小于的树苗棵数是( ).
A. 360 B. 600 C. 840 D. 1320
6.一只不透明的盒子中装有形状、大小相同的4只球,其中有2只白球,2只黑球,若从中随机摸出两只球,则它们颜色不同的概率是( )
A. B. C. D.
7. 函数的定义域是( )
A. B.
C. D.
8. 如图,已知向量,那么下列结论正确的是( )
B.
C. D.
9. 在中,已知,,,则( )
A. B. C. D.
10.复数在复平面内对应的点在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
11.幂函数为偶函数,且在上为减函数的是( )
A. B.
C. D.
12.抛掷两枚质地均匀的硬币,设事件“第一枚硬币正面向上”,设事件“第二枚硬币正面向上”,则( )
A. 事件与互为对立事件 B. 件与为互斥事件
C. 事件与事件相等 D. 事件与相互独立
13. 运动员甲10次射击成绩(单位:环)如下:7,8,9,7,4,8,9,9,7,2,则下列关于这组数据说法不正确的是( ).
A. 众数为7和9 B. 平均数为7
C. 中位数为7 D. 方差为
14.已知m,n表示两条不同直线,表示平面,下列说法正确的是
A. 若则 B. 若,,则
C. 若,,则 D. 若,,则
16.某工厂生产甲、乙、丙三种型号的产品,产品数量之比为3:5:7,现用分层抽样的方法抽出容量为n的样本,其中甲种产品有18件,则样本容量n=( )
A. 45 B. 54 C. 90 D. 126
17. 将函数的图象向右平移个长度单位,再将所得图象上所有点的横坐标变为原来的2倍(纵坐标不变),得到函数的图象,则的解析式为( )
A. B.
C. D.
18.关于x的不等式的解集为,则实数a的值为( )
A. B. C. D. 4
19. 知两点,与平行,且方向相反的向量可能是( )
A. B.
C. D.
20. 已知函数在上单调递减,则实数的取值范围是( )
A. B. C. D.
21. 已知,则( )
A. B. C. 3 D.
22.在长方体中,点E为的中点,,且,则异面直线AE与BC所成角的余弦值为( )
A. B. C. D.
23.已知是定义在上的偶函数,当时,,则时,( )
A. B.
C. D.
24.设,,,则( )
A. B. C. D.
25.在,其内角的对边分别为,若,则的形状是( )
A. 等腰三角形 B. 直角三角形
C. 等腰直角三角形 D. 等腰或直角三角形
26.已知平面,直线m,n.( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
27.党的二十大报告指出,“坚持精准治污、科学治污、依法治污,持续深入打好蓝天、碧水、净土保卫战.加强污染物协同控制,基本消除重污染天气.”按照相关规定,某化工厂产生的废气中的某类污染物经过过滤装置的处理,含量降至过滤前的以下才能排放.已知过滤过程中,废气中污染物的含量(单位:mg/L)与时间(单位:min)的关系为,其中,是常数.若时,该类污染物的含量降为过滤前的,那么废气至少需要过滤( )才能排放(结果保留整数,参考数据:).
A. 7 B. 8 C. 9 D. 10
28.某公司为了解用户对其产品的满意度,从甲、乙两地区分别随机调查了100个用户,根据用户对产品的满意度评分,分别得到甲地区和乙地区用户满意度评分的频率分布直方图.
若甲地区和乙地区用户满意度评分中位数分别为,,平均数分别为,,则( )
, B. ,
C. , D.,
二、解答题(本大题共2小题,共16分,解答应写出文字说明,证明过程或演算步骤。)
29.(本小题满分8分)在①、②这两个条件中任选一个,补充到下面问题中,并进行作答.
在中,内角、、的对边分别为、、,,, .
(1)求角、、的大小;
(2)求的周长和面积.
30.(本小题满分8分)如图,四棱柱的底面是正方形,侧面是菱形,,平面平面,E,F分别为的中点.
(1)求证:平面;
(2)求与平面所成角的正切值.
024年江苏省普通高中学业水平合格性考试
数学全真模拟试卷01
(考试时间:75分钟 满分100分)
一、选择题(本大题共28小题,每小题3分,共84分。每个小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不给分)
1.设集合,,则( )
A. B. C. D.
【答案】B
【解析】由题设有,
故选:B
2. 若命题:,则命题的否定为( )
A. B.
C. D.
【答案】D
【解析】根据存在量词的否定是全称量词可得命题的否定为.
故选:D
3. 设a,b,c∈R,其中正确的是( )
A. 若,则 B. 若, 则
C. 若,则 D. 若,则
【答案】A
【解析】当时,BD都不正确,当时C错误,由不等式的基本性质得A正确;
故选:A
4.若角的终边经过点,则( )
A. B. C. D.
【答案】A
【解析】点到原点的距离为,所以,
故选:A.
5.某部门为了了解一批树苗的生长情况,在3000棵树苗中随机抽取200棵,统计这200棵树苗的高度,并绘制了频率分布直方图(如图),那么根据该图可推测,在这3000棵树苗中高度小于的树苗棵数是( ).
A. 360 B. 600 C. 840 D. 1320
【答案】B
【解析】由频率分布直方图可得,小于的树苗的频率,所以可推测,3000棵树苗中高度小于的树苗棵数
故选:B
6.一只不透明的盒子中装有形状、大小相同的4只球,其中有2只白球,2只黑球,若从中随机摸出两只球,则它们颜色不同的概率是( )
A. B. C. D.
【答案】B
【解析】设从中随机摸出两只球,它们颜色不同为事件A,
∵基本事件总数为6,
事件A中包含的基本事件数为4,
∴P(A)==.
故选:B.
7. 函数的定义域是( )
A. B.
C. D.
【答案】D
【解析】的定义域满足,解得.
故选:D
8. 如图,已知向量,那么下列结论正确的是( )
A. B. C. D.
【答案】B
【解析】根据向量加法的三角形法则,向量首尾顺次相连,所以根据图形可知,与向量反向且相等,所以.
故选:B.
9. 在中,已知,,,则( )
A. B. C. D.
【答案】A
【解析】在中,已知,,,
由余弦定理得:,
故选:A
10.复数在复平面内对应的点在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
【答案】D
【解析】,故对应的点为
故选:D.
11.幂函数为偶函数,且在上为减函数的是( )
A. B.
C. D.
【答案】A
【解析】对A:,则,
故偶函数,且在上为减函数,A正确;
对B:的定义域为,即定义域不关于原点对称,故为非奇非偶函数,B错误;
对C:,
故为偶函数,且在上为增函数,C正确;
对D:,故为奇函数,D错误.
故选:A.
12.抛掷两枚质地均匀的硬币,设事件“第一枚硬币正面向上”,设事件“第二枚硬币正面向上”,则( )
A. 事件与互为对立事件 B. 件与为互斥事件
C. 事件与事件相等 D. 事件与相互独立
【答案】D
【解析】抛掷两枚质地均匀的硬币,
设事件 “第一枚硬币正面向上”,
设事件 “第二枚硬币正面向上”,
事件发生与否与事件无关,事件发生与否与事件无关,
事件与事件相互独立.
故选:D.
13. 运动员甲10次射击成绩(单位:环)如下:7,8,9,7,4,8,9,9,7,2,则下列关于这组数据说法不正确的是( ).
A. 众数为7和9 B. 平均数为7
C. 中位数为7 D. 方差为
【答案】C
【解析】由题意,这组数据中7和9都出现3次,其余数出现次数没超过3次,
故众数为7和9,A正确;
计算平均数为 ,故B正确;
将10次射击成绩从小到大排列为:2,4,7, 7, 7,8,8,9,9,9,
则中位数为 ,故C错误;
方差为,
故D正确,
故选:C
14.已知m,n表示两条不同直线,表示平面,下列说法正确的是
A. 若则 B. 若,,则
C. 若,,则 D. 若,,则
【答案】B
【解析】
线面垂直,则有该直线和平面内所有的直线都垂直,故B正确.
故选:B
15.函数的定义域为( )
A. B.
C. D.
【答案】B
【解析】由有意义,则,
该不等式等价于,解得.
故选:B.
16.某工厂生产甲、乙、丙三种型号的产品,产品数量之比为3:5:7,现用分层抽样的方法抽出容量为n的样本,其中甲种产品有18件,则样本容量n=( )
A. 45 B. 54 C. 90 D. 126
【答案】C
【解析】A种型号产品所占的比例为,
,故样本容量n=90.
故选C.
17. 将函数的图象向右平移个长度单位,再将所得图象上所有点的横坐标变为原来的2倍(纵坐标不变),得到函数的图象,则的解析式为( )
A. B.
C. D.
【答案】D
【解析】函数的图象向右平移个长度单位得到,
再将所得图象上所有点的横坐标变为原来的2倍(纵坐标不变)得到
.
故选:D
18.关于x的不等式的解集为,则实数a的值为( )
A. B. C. D. 4
【答案】D
【解析】由且不等于1,
由题意得,,解得.
故选:D.
19. 知两点,与平行,且方向相反的向量可能是( )
A. B.
C. D.
【答案】A
【解析】,
A选项, ,故满足题意
B、C、D选项中的不与平行
故选:A
20. 已知函数在上单调递减,则实数的取值范围是( )
A. B. C. D.
【答案】D
【解析】由题意知函数在上单调递减,
而图象开口向上,对称轴为,则,
即实数的取值范围是,
故选:D
21. 已知,则( )
A. B. C. 3 D.
【答案】A
【解析】.
故选:A.
22.在长方体中,点E为的中点,,且,则异面直线AE与BC所成角的余弦值为( )
A. B. C. D.
【答案】C
【解析】
连接,由可得或其补角即为异面直线AE与BC所成角,又面,面,则,
则,同理可得,,则,,
则异面直线AE与BC所成角的余弦值为.
故选:C.
23.已知是定义在上的偶函数,当时,,则时,( )
A. B.
C. D.
【答案】A
【解析】当时,,则 ①
又因为是定义在上的偶函数,
所以 ②
所以由①②得:当时,.
故选:A.
24.设,,,则( )
A. B. C. D.
【答案】C
【解析】∵,
又,
∴.
故选:C.
25.在,其内角的对边分别为,若,则的形状是( )
A. 等腰三角形 B. 直角三角形
C. 等腰直角三角形 D. 等腰或直角三角形
【答案】A
【解析】因为在,,
所以,
又,
所以,,
所以为等腰三角形.
故选:A.
26.已知平面,直线m,n.( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
【答案】D
【解析】对A,若,则或,故A错误;
对B,若,则和平行、相交或在平面内,故B错误;
对C,若,则平行、相交或异面,故C错误;
对D,若,则,故D正确.
故选:D.
27.党的二十大报告指出,“坚持精准治污、科学治污、依法治污,持续深入打好蓝天、碧水、净土保卫战.加强污染物协同控制,基本消除重污染天气.”按照相关规定,某化工厂产生的废气中的某类污染物经过过滤装置的处理,含量降至过滤前的以下才能排放.已知过滤过程中,废气中污染物的含量(单位:mg/L)与时间(单位:min)的关系为,其中,是常数.若时,该类污染物的含量降为过滤前的,那么废气至少需要过滤( )才能排放(结果保留整数,参考数据:).
A. 7 B. 8 C. 9 D. 10
【答案】C
【解析】依题意可得,所以,两边取对数可得,
所以,则,
所以,令,即,所以,
即,
所以,
所以废气至少需要过滤才能排放.
故选:C
28.某公司为了解用户对其产品的满意度,从甲、乙两地区分别随机调查了100个用户,根据用户对产品的满意度评分,分别得到甲地区和乙地区用户满意度评分的频率分布直方图.
若甲地区和乙地区用户满意度评分中位数分别为,,平均数分别为,,则( )
A. , B. , C. , D. ,
【答案】C
【解析】由频率分布直方图得:
甲地区,的频率为:,
,的频率为,
甲地区用户满意度评分的中位数,
甲地区的平均数.
乙地区,的频率为:,
,的频率为:,
乙地区用户满意度评分的中位数,
乙地区的平均数.
,.
故选:C.
二、解答题(本大题共2小题,共16分,解答应写出文字说明,证明过程或演算步骤。)
29.(本小题满分8分)在①、②这两个条件中任选一个,补充到下面问题中,并进行作答.
在中,内角、、的对边分别为、、,,, .
(1)求角、、的大小;
(2)求的周长和面积.
【答案】(1),,;(2)周长为,面积为.
【解析】选①:
(1)因为,,所以,
则,
因为,所以,,
因为,
所以,.
(2)因为,,,,
所以,的周长为,
的面积.
选②:
(1)联立,解得,
因为,,所以,.
(2)因为,,,,
所以,周长为,
的面积.
30.(本小题满分8分)如图,四棱柱的底面是正方形,侧面是菱形,,平面平面,E,F分别为的中点.
(1)求证:平面;
(2)求与平面所成角的正切值.
【答案】(1)证明见解析;(2).
【解析】(1)设中点为G,连接,
因为E,G分别为的中点,
所以,
在正方形中,F是的中点,
所以,且,
所以且,
所以四边形是平行四边形,
所以,
因为平面平面,
所以平面.
(2)过作于M,过E作于H,连接,则,
因为平面平面,且平面平面,
平面,所以平面,
所以是在平面内的射影,
所以为直线与平面所成的角,
设正方形的边长为a,
因为侧面是菱形,,所以,
又因为且E是的中点,所以,
在正方形中,F为中点,H为的四等分点,,
所以在直角三角形中,,
所以与平面所成角的正切值为.
同课章节目录
