第22章一元二次方程单元达标测试卷2023-2024学年华东师大版九年级数学上册(含解析)
文档属性
| 名称 | 第22章一元二次方程单元达标测试卷2023-2024学年华东师大版九年级数学上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 246.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 14:13:51 | ||
图片预览




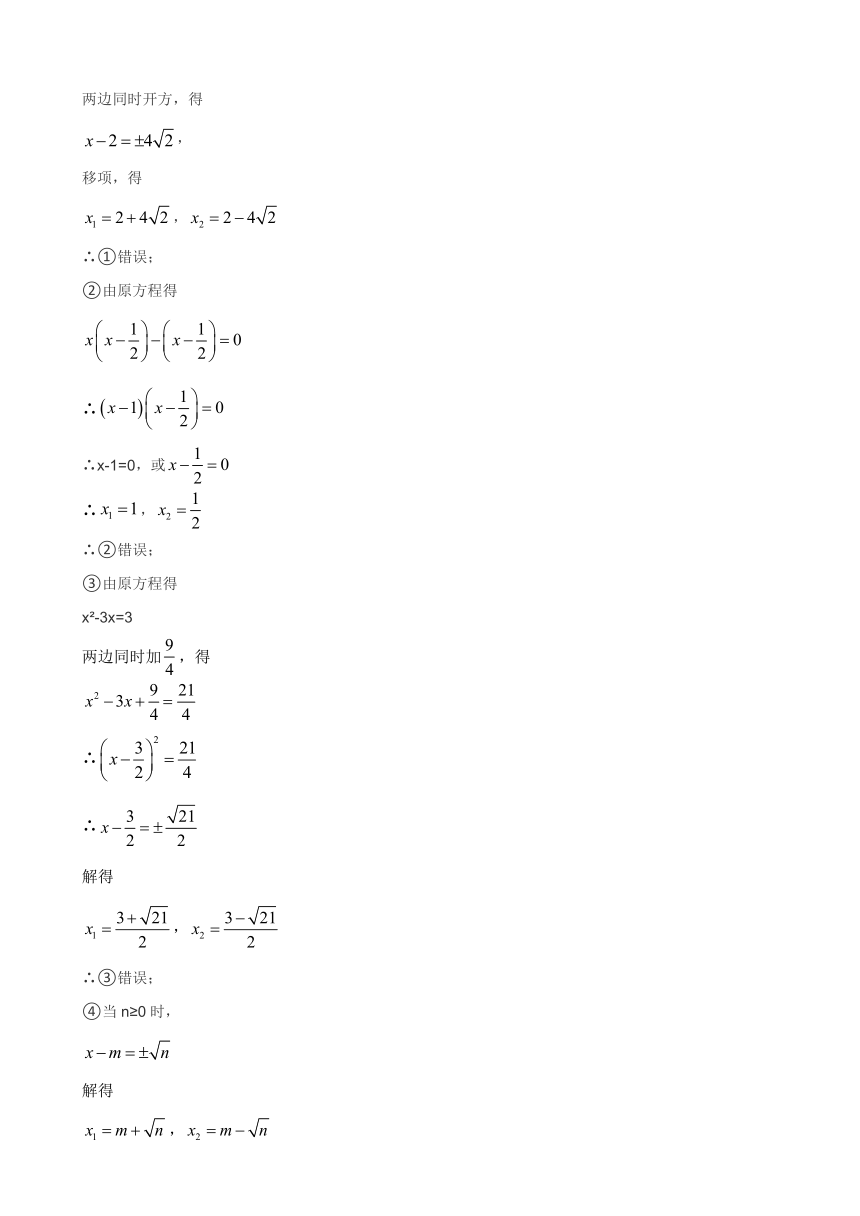
文档简介
华东师大版九年级数学上册第22章一元二次方程单元达标测试卷
一、单选题
1.若一元二次方程的常数项是0,则的值是( )
A.2或-2 B.2 C.-2 D.4
2.若关于x的方程mx2-2x+1=0是一元二次方程,则( )
A.m>0 B.m≥0 C.m=1 D.m≠0
3.已知一元二次方程的一般式为 ,则一元二次方程x2-5=0中b的值为( )
A.1 B.0 C.-5 D.5
4.某产品成本价为100万元,由于改进技术,成本连续降低,每次降低 %,连续两次降低后成本为64万元,则 的值为( )
A.10 B.15 C.18 D.20
5.给出以下方程的解题过程,其中正确的有( )
①解方程 (x﹣2)2=16,两边同时开方得x﹣2=±4,移项得x1=6,x2=﹣2;②解方程x(x﹣ )=(x﹣ ),两边同时除以(x﹣ )得x=1,所以原方程的根为x1=x2=1;③解方程(x﹣2)(x﹣1)=5,由题得x﹣2=1,x﹣1=5,解得x1=3,x2=6;④方程(x﹣m)2=n的解是x1=m+ ,x2=m﹣ .
A.0个 B.2个 C.3个 D.4个
6.一种商品原价100元,经过两次降价后的售价是60元,设平均每次降价的百分率为 ,那么所列方程正确的是( )
A. B. C. D.
7.用配方法解一元二次方程x2-4x+3=0时可配方得( )
A.(x-2)2=7 B.(x-2)2=1 C.(x+2)2=1 D.(x+2)2=2
8.如图,学校课外生物小组试验园地的形状是长米、宽米的矩形,为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为平方米.则小道的宽为多少米?若设小道的宽为米,则根据题意,列方程为( )
A. B.
C. D.
9.一元二次方程 有两个相等的实数根,那么实数 的取值为( ).
A. B. C. D.
10.电影《我和我的祖国》讲述了普通人与国家之间息息相关的动人故事.一上映就获得全国人民的追捧,第一天票房约3亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达10亿元,若把平均每天票房的增长率记作x,则可以列方程为( )
A. B. C. D.
二、填空题
11.方程 是关于x的一元二次方程,则m= .
12.为把我市创建成全国文明城市,某社区积极响应市政府号召,准备在 一块正方形的空地上划出部分区域栽种鲜花,如图中的阴影“┛”带,鲜花带一边宽1m.另一边宽2m,剩余空地的面积为18m2,求原正方形空地的边长 m,可列方程为 .
13.某小组同学,新年时每人互送贺年卡一张,共送贺年卡56张,这个小组共有 人.
14.若x1、x2是一元二次方程x2-3x-3=0的两个根,则,x1+x2的值是 ,
三、计算题
15.(1)x2﹣3x=10 (2)3x2﹣x﹣4=0.
四、解答题
16.夏津某一企业2014年完成工业总产值100万元,如果要在2016年达到169万元,那么2014年到2016年的工业总产值年平均增长率是多少?计划2018年工业总产值要达到280万元,若继续保持上面的增长率,该目标是否可以完成?
17.解方程:x2+4x﹣2=0
18.某市百货商店服装部在销售中发现“米奇”童装平均每天可售出20件,每件获利40元。为了迎接“六一”儿童节和扩大销售,增加利润,商场决定采取适当的降价措施,经过市场调查,发现如果每件童装每降价1元,则平均每天可多售出2件,要想平均每天在销售这种童装上获利1200元,并且尽快减少库存,那么每件童装应降价多少元?
19.已知关于x的一元二次方程 (1-2k)x2-2-1=0有两个不相等的实数根,求k的取值范围.
五、综合题
20.如图,用一段77米的篱笆围成三个一边靠墙、大小相同的矩形羊圈,每个矩形都有一个1米的门,墙的最大可用长度为30米.
(1)如果羊圈的总面积为300平方米,求边 的长;
(2)羊圈的总面积能为500平方米吗?若能,请求出边 的长;若不能,说明理由.
21.已知 、 是关于 的一元二次方程 的两个实数根,其中 为非负整数,点 是一次函数 与反比例函数 的图象的交点,且 、 为常数.
(1)求 的值;
(2)求一次函数与反比例函数的解析式.
22.已知关于x的二次方程有两个不相等的实数根.
(1)求m的取值范围;
(2)如果m为正整数,求此方程的根.
23.已知:x1,x2是x2+8x+m=0的两个实数根,且=60求.
(1)m的值;
(2)
答案解析部分
1.【答案】C
【解析】【解答】解:一元二次方程程的常数项为0,
,
,
,
故答案为:C.
【分析】一元二次方程ax2+bx+c=0(a、b、c是常数,且a≠0),其中a是二次项系数、b是一次项系数、c是常数项,据此并结合题意可得,求解即可.
2.【答案】D
【解析】【解答】解:由题意可得:
m≠0
故答案为:D
【分析】根据一元二次方程方程的定义即可求出答案.
3.【答案】B
【解析】【解答】∵一元二次方程的一般式为 ,
对于一元二次方程x2-5=0中没有一次项,
故b的值为0,
故答案为:B.
【分析】对照一元二次方程的一般形式,根据没有项的系数为0求解即可.
4.【答案】D
【解析】【解答】解:设平均每次降低成本的百分率为x%,根据题意得100(1-x%)(1-x%)=64,
解得x=20或180(不合题意,舍去)
故答案为:D.
【分析】根据数量下降x%就变为原来的(1-x%),列方程求解即可。
5.【答案】A
【解析】【解答】解:①由原方程得
两边同时开方,得
,
移项,得
,
∴①错误;
②由原方程得
∴
∴x-1=0,或
∴,
∴②错误;
③由原方程得
x -3x=3
两边同时加,得
∴
∴
解得
,
∴③错误;
④当n≥0时,
解得
,
当n<0时,方程无解;
∴④错误.
故答案为:A.
【分析】①在计算时,不能漏掉数字;②在等式的性质中,是“两边同时除以一个不为0的数”,可能为0;③因式分解法解方程时,等号右边一定是0,才能利用“若ab=0,则a=0,或b=0”的原理解题;④两边开方时,要保证被开方数是非负数.
6.【答案】C
【解析】【解答】解; ;
故答案为:C.
【分析】设两次降价的百分比均为x,由题意得出:x满足的方程即可得出,解之即可。
7.【答案】B
【解析】【分析】此题考查了配方法解一元二次方程,解题时要先把常数项移项、二次项系数化1,然后左右两边加上一次项系数一半的平方.
【解答】∵x2-4x+3=0,
∴x2-4x=-3,
∴x2-4x+4=-3+4,
∴(x-2)2=1.
故选B.
【点评】配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
8.【答案】A
【解析】【解答】解:
A:把道路平移如图情形,则种植部分为长方形,长为(40-2x)米,宽为(34-x)米,
列方程为: ,A正确;
B:方程左边少减去了一个34x,B错误;
C:平移后,弄错了种植部分的长和宽,C错误;
D:横纵小道交叉部分重复计算了,D错误。
故答案为:A
【分析】种植面积等于长方形面积减去3条小道的面积,不能有遗漏,特别要注意横纵小道交叉部分不能重复计算,也可用平移法把小道部分拼合在一起,种植部分则有一个长方形,运用长方形面积公式可列方程。
9.【答案】C
【解析】【解答】解:∵一元二次方程x2+2x+c=0有两个相等的实数根,
∴b2-4ac=0,即4-4c=0,
解得:c=1.
故答案为:C.
【分析】利用一元二次方程根的判别式求出4-4c=0,再计算求解即可。
10.【答案】D
【解析】【解答】解:设增长率为x,由题意可得出,第二天的票房为3(1+x),第三天的票房为3(1+x)2,
根据题意可列方程为 .
故答案为:D.
【分析】根据题意分别用含x式子表示第二天,第三天的票房数,将三天的票房相加得到票房总收入,即可得出答案.
11.【答案】m=2
【解析】【解答】解:由题意得:m=2且m+2≠0,
由解得得m=2且m≠ 2,
∴m=2.
故答案为:m=2.
【分析】本题根据一元二次方程的定义求解.一元二次方程必须满足两个条件:(1)未知数的最高次数是2;(2)二次项系数不为0.由这两个条件得到相应的关系式,再求解即可.
12.【答案】
【解析】【解答】设原正方形的边长为x,则长方形的长为x-1,宽为x-2,
根据题意,得(x-1)(x-2)=18,
故答案为:(x-1)(x-2)=18.
【分析】设原正方形的边长为x,则长方形的长为x-1,宽为x-2,再根据剩余空地的面积为18m2,列方程即可.
13.【答案】8
【解析】【解答】设这个小组有x人,那么每个人送的贺卡为x-1张,根据题意得:
x(x-1)=56
解得x=-7(不合题意舍去),x=8
【分析】设这个小组有x人,那么每个人送的贺卡为x-1张,那么根据题意可得出方程为x(x-1),即可列出方程求解.注意根据实际意义进行值的取舍.
14.【答案】3
【解析】【解答】解:根据题意可知,x1+x2=3
【分析】根据一元二次方程根与系数的关系,即可运算得到答案。
15.【答案】解:(1)方程变形得:x2﹣3x﹣10=0,即(x﹣5)(x+2)=0,
可得x﹣5=0或x+2=0,
解得:x1=5,x2=﹣2;
(2)这里a=3,b=,c=﹣4,
∵△=2+48=50,
∴x=,
则x1=,x2=.
【解析】【分析】
(1)把等号右边的常数10移到等号左边,进行因式分解,得到两个一元一次方程,求解即可;
(2)确定a、b、c的值代入一元二次方程的求根公式即可求出方程的解.
16.【答案】解:设设2014到2016年的工业平均增长率为x,根据题意可得:
则100(1+x)2=169,
所以(1+x)2=1.69
解得:x1=0.3,x2=﹣2.3(不合题意舍去.
故平均增长速度为30%.
169(1+0.3)2=285.81>280,
答:继续保持上面的增长率,该目标可以完成
【解析】【分析】用增长后的量=增长前的量×(1+增长率).首先设2014到2016年的工业平均增长率为x,则2016年的工业总产值是100(1+x)2,根据题意利用一元二次方程解答即可.再计算出增长率后根据增长率可求是否能完成.
17.【答案】解:x2+4x﹣2=0,
b2﹣4ac=42﹣4×1×(﹣2)=24,
x=,
x1=﹣2+,x2=﹣2﹣;
【解析】【分析】求出b2﹣4ac的解集,再根据找不等式组解集的规律找出不等式组的解集即可;
18.【答案】解:设每件童装应降价x元,由题意得:
(40-x)(20+2x)=1200,
解得:x1=20,x2=10,
当x=20时,20+2x=60(件),
当x=10时,20+2x=40(件),
∵60>40,
∴x2=10舍去.
答:每件童装应降价20元.
【解析】【分析】设每件童装应降价x元,由题意得:(40-x)(20+2x)=1200,解一元二次方程,再由尽快减少库存得到答案.
19.【答案】解:由题意得:1﹣2k≠0即k≠,
k+1≥0,即k≥﹣1
△=b2﹣4ac=(﹣2)2﹣4×(1﹣2k)×(﹣1)=8﹣4k>0,
∴k<2
综合所述,得﹣1≤k<2且k≠,
【解析】【分析】一元二次方程有两个不相等的实数根,则△=b2﹣4ac>0,结合一元二次方程的定义,求出k的取值范围.
20.【答案】(1)解:设AB=x米,由题意可得: ,
∴ ,
解得: ,
∵墙的最大可用长度为30米,且当x=5时, ,
∴ ,
答:边AB的长为15米;
(2)解:由(1)可得: ,
化简得: ,
∴ ,
∴羊圈的总面积不能为500平方米.
【解析】【分析】(1)设AB=x米,由题意可得x(80-4x)=300,求出x的值,然后根据墙的最大可用长度为30米对x的值进行取舍;
(2)由(1)可得x(80-4x)=500,求解即可判断.
21.【答案】(1)解:依题意,得 且 ,解得 且 .∵ 为非负整数,
∴
(2)解:当 时,原方程化为 ,
∴ ,
解得 ,
∴ ,
把 和 代入 ,
解得 ,
∴一次函数的解析式是 ,
把 代入 ,
解得 ,
∴反比例函数的解析式是
【解析】【分析】(1)已知一元二次方程有两个实数根,可得出k≠0且b2-4ac≥0,建立关于k的不等式,再根据k为非负整数,就可得出k的值。
(2)将k=1代入方程,再解方程,求出x的值,就可得出点A的坐标,再将k=1和点A的坐标分别代入两函数解析式,就可求得结果。
22.【答案】(1)解:∵关于x的二次方程有两个不相等的实数根,
∴ >0,
∴,
解得;
∵,
∴且;
(2)解:∵且m≠0,m为正整数,
∴m=1,
∴该方程为,
解得x1=0,x2=-1.
【解析】【分析】(1)利用一元二次方程根的判别式列出不等式求解即可;
(2)将m的值代入方程,再求解即可。
23.【答案】(1)解: x1,x2是x2+8x+m=0的两个实数根,
解得:
经检验:符合题意.
(2)解:
方程的两个根都为负数,
设
即
【解析】【分析】(1)利用一元二次方程根与系数的关系,可表示出x1+x2和x1x2,再将等式根据完全平方公式转化为(x1+x2)2-2x1x2=60,然后代入可得到关于m的方程,解方程求出m的值;
(2)利用m的值可得x1+x2和x1x2的值,由此可推出方程的两个根都为负数;设,两边同时平方,将等式的右边转化为含有x1+x2和x1x2的代数式,将其代入,可求出y的值,即可求解.
一、单选题
1.若一元二次方程的常数项是0,则的值是( )
A.2或-2 B.2 C.-2 D.4
2.若关于x的方程mx2-2x+1=0是一元二次方程,则( )
A.m>0 B.m≥0 C.m=1 D.m≠0
3.已知一元二次方程的一般式为 ,则一元二次方程x2-5=0中b的值为( )
A.1 B.0 C.-5 D.5
4.某产品成本价为100万元,由于改进技术,成本连续降低,每次降低 %,连续两次降低后成本为64万元,则 的值为( )
A.10 B.15 C.18 D.20
5.给出以下方程的解题过程,其中正确的有( )
①解方程 (x﹣2)2=16,两边同时开方得x﹣2=±4,移项得x1=6,x2=﹣2;②解方程x(x﹣ )=(x﹣ ),两边同时除以(x﹣ )得x=1,所以原方程的根为x1=x2=1;③解方程(x﹣2)(x﹣1)=5,由题得x﹣2=1,x﹣1=5,解得x1=3,x2=6;④方程(x﹣m)2=n的解是x1=m+ ,x2=m﹣ .
A.0个 B.2个 C.3个 D.4个
6.一种商品原价100元,经过两次降价后的售价是60元,设平均每次降价的百分率为 ,那么所列方程正确的是( )
A. B. C. D.
7.用配方法解一元二次方程x2-4x+3=0时可配方得( )
A.(x-2)2=7 B.(x-2)2=1 C.(x+2)2=1 D.(x+2)2=2
8.如图,学校课外生物小组试验园地的形状是长米、宽米的矩形,为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为平方米.则小道的宽为多少米?若设小道的宽为米,则根据题意,列方程为( )
A. B.
C. D.
9.一元二次方程 有两个相等的实数根,那么实数 的取值为( ).
A. B. C. D.
10.电影《我和我的祖国》讲述了普通人与国家之间息息相关的动人故事.一上映就获得全国人民的追捧,第一天票房约3亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达10亿元,若把平均每天票房的增长率记作x,则可以列方程为( )
A. B. C. D.
二、填空题
11.方程 是关于x的一元二次方程,则m= .
12.为把我市创建成全国文明城市,某社区积极响应市政府号召,准备在 一块正方形的空地上划出部分区域栽种鲜花,如图中的阴影“┛”带,鲜花带一边宽1m.另一边宽2m,剩余空地的面积为18m2,求原正方形空地的边长 m,可列方程为 .
13.某小组同学,新年时每人互送贺年卡一张,共送贺年卡56张,这个小组共有 人.
14.若x1、x2是一元二次方程x2-3x-3=0的两个根,则,x1+x2的值是 ,
三、计算题
15.(1)x2﹣3x=10 (2)3x2﹣x﹣4=0.
四、解答题
16.夏津某一企业2014年完成工业总产值100万元,如果要在2016年达到169万元,那么2014年到2016年的工业总产值年平均增长率是多少?计划2018年工业总产值要达到280万元,若继续保持上面的增长率,该目标是否可以完成?
17.解方程:x2+4x﹣2=0
18.某市百货商店服装部在销售中发现“米奇”童装平均每天可售出20件,每件获利40元。为了迎接“六一”儿童节和扩大销售,增加利润,商场决定采取适当的降价措施,经过市场调查,发现如果每件童装每降价1元,则平均每天可多售出2件,要想平均每天在销售这种童装上获利1200元,并且尽快减少库存,那么每件童装应降价多少元?
19.已知关于x的一元二次方程 (1-2k)x2-2-1=0有两个不相等的实数根,求k的取值范围.
五、综合题
20.如图,用一段77米的篱笆围成三个一边靠墙、大小相同的矩形羊圈,每个矩形都有一个1米的门,墙的最大可用长度为30米.
(1)如果羊圈的总面积为300平方米,求边 的长;
(2)羊圈的总面积能为500平方米吗?若能,请求出边 的长;若不能,说明理由.
21.已知 、 是关于 的一元二次方程 的两个实数根,其中 为非负整数,点 是一次函数 与反比例函数 的图象的交点,且 、 为常数.
(1)求 的值;
(2)求一次函数与反比例函数的解析式.
22.已知关于x的二次方程有两个不相等的实数根.
(1)求m的取值范围;
(2)如果m为正整数,求此方程的根.
23.已知:x1,x2是x2+8x+m=0的两个实数根,且=60求.
(1)m的值;
(2)
答案解析部分
1.【答案】C
【解析】【解答】解:一元二次方程程的常数项为0,
,
,
,
故答案为:C.
【分析】一元二次方程ax2+bx+c=0(a、b、c是常数,且a≠0),其中a是二次项系数、b是一次项系数、c是常数项,据此并结合题意可得,求解即可.
2.【答案】D
【解析】【解答】解:由题意可得:
m≠0
故答案为:D
【分析】根据一元二次方程方程的定义即可求出答案.
3.【答案】B
【解析】【解答】∵一元二次方程的一般式为 ,
对于一元二次方程x2-5=0中没有一次项,
故b的值为0,
故答案为:B.
【分析】对照一元二次方程的一般形式,根据没有项的系数为0求解即可.
4.【答案】D
【解析】【解答】解:设平均每次降低成本的百分率为x%,根据题意得100(1-x%)(1-x%)=64,
解得x=20或180(不合题意,舍去)
故答案为:D.
【分析】根据数量下降x%就变为原来的(1-x%),列方程求解即可。
5.【答案】A
【解析】【解答】解:①由原方程得
两边同时开方,得
,
移项,得
,
∴①错误;
②由原方程得
∴
∴x-1=0,或
∴,
∴②错误;
③由原方程得
x -3x=3
两边同时加,得
∴
∴
解得
,
∴③错误;
④当n≥0时,
解得
,
当n<0时,方程无解;
∴④错误.
故答案为:A.
【分析】①在计算时,不能漏掉数字;②在等式的性质中,是“两边同时除以一个不为0的数”,可能为0;③因式分解法解方程时,等号右边一定是0,才能利用“若ab=0,则a=0,或b=0”的原理解题;④两边开方时,要保证被开方数是非负数.
6.【答案】C
【解析】【解答】解; ;
故答案为:C.
【分析】设两次降价的百分比均为x,由题意得出:x满足的方程即可得出,解之即可。
7.【答案】B
【解析】【分析】此题考查了配方法解一元二次方程,解题时要先把常数项移项、二次项系数化1,然后左右两边加上一次项系数一半的平方.
【解答】∵x2-4x+3=0,
∴x2-4x=-3,
∴x2-4x+4=-3+4,
∴(x-2)2=1.
故选B.
【点评】配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
8.【答案】A
【解析】【解答】解:
A:把道路平移如图情形,则种植部分为长方形,长为(40-2x)米,宽为(34-x)米,
列方程为: ,A正确;
B:方程左边少减去了一个34x,B错误;
C:平移后,弄错了种植部分的长和宽,C错误;
D:横纵小道交叉部分重复计算了,D错误。
故答案为:A
【分析】种植面积等于长方形面积减去3条小道的面积,不能有遗漏,特别要注意横纵小道交叉部分不能重复计算,也可用平移法把小道部分拼合在一起,种植部分则有一个长方形,运用长方形面积公式可列方程。
9.【答案】C
【解析】【解答】解:∵一元二次方程x2+2x+c=0有两个相等的实数根,
∴b2-4ac=0,即4-4c=0,
解得:c=1.
故答案为:C.
【分析】利用一元二次方程根的判别式求出4-4c=0,再计算求解即可。
10.【答案】D
【解析】【解答】解:设增长率为x,由题意可得出,第二天的票房为3(1+x),第三天的票房为3(1+x)2,
根据题意可列方程为 .
故答案为:D.
【分析】根据题意分别用含x式子表示第二天,第三天的票房数,将三天的票房相加得到票房总收入,即可得出答案.
11.【答案】m=2
【解析】【解答】解:由题意得:m=2且m+2≠0,
由解得得m=2且m≠ 2,
∴m=2.
故答案为:m=2.
【分析】本题根据一元二次方程的定义求解.一元二次方程必须满足两个条件:(1)未知数的最高次数是2;(2)二次项系数不为0.由这两个条件得到相应的关系式,再求解即可.
12.【答案】
【解析】【解答】设原正方形的边长为x,则长方形的长为x-1,宽为x-2,
根据题意,得(x-1)(x-2)=18,
故答案为:(x-1)(x-2)=18.
【分析】设原正方形的边长为x,则长方形的长为x-1,宽为x-2,再根据剩余空地的面积为18m2,列方程即可.
13.【答案】8
【解析】【解答】设这个小组有x人,那么每个人送的贺卡为x-1张,根据题意得:
x(x-1)=56
解得x=-7(不合题意舍去),x=8
【分析】设这个小组有x人,那么每个人送的贺卡为x-1张,那么根据题意可得出方程为x(x-1),即可列出方程求解.注意根据实际意义进行值的取舍.
14.【答案】3
【解析】【解答】解:根据题意可知,x1+x2=3
【分析】根据一元二次方程根与系数的关系,即可运算得到答案。
15.【答案】解:(1)方程变形得:x2﹣3x﹣10=0,即(x﹣5)(x+2)=0,
可得x﹣5=0或x+2=0,
解得:x1=5,x2=﹣2;
(2)这里a=3,b=,c=﹣4,
∵△=2+48=50,
∴x=,
则x1=,x2=.
【解析】【分析】
(1)把等号右边的常数10移到等号左边,进行因式分解,得到两个一元一次方程,求解即可;
(2)确定a、b、c的值代入一元二次方程的求根公式即可求出方程的解.
16.【答案】解:设设2014到2016年的工业平均增长率为x,根据题意可得:
则100(1+x)2=169,
所以(1+x)2=1.69
解得:x1=0.3,x2=﹣2.3(不合题意舍去.
故平均增长速度为30%.
169(1+0.3)2=285.81>280,
答:继续保持上面的增长率,该目标可以完成
【解析】【分析】用增长后的量=增长前的量×(1+增长率).首先设2014到2016年的工业平均增长率为x,则2016年的工业总产值是100(1+x)2,根据题意利用一元二次方程解答即可.再计算出增长率后根据增长率可求是否能完成.
17.【答案】解:x2+4x﹣2=0,
b2﹣4ac=42﹣4×1×(﹣2)=24,
x=,
x1=﹣2+,x2=﹣2﹣;
【解析】【分析】求出b2﹣4ac的解集,再根据找不等式组解集的规律找出不等式组的解集即可;
18.【答案】解:设每件童装应降价x元,由题意得:
(40-x)(20+2x)=1200,
解得:x1=20,x2=10,
当x=20时,20+2x=60(件),
当x=10时,20+2x=40(件),
∵60>40,
∴x2=10舍去.
答:每件童装应降价20元.
【解析】【分析】设每件童装应降价x元,由题意得:(40-x)(20+2x)=1200,解一元二次方程,再由尽快减少库存得到答案.
19.【答案】解:由题意得:1﹣2k≠0即k≠,
k+1≥0,即k≥﹣1
△=b2﹣4ac=(﹣2)2﹣4×(1﹣2k)×(﹣1)=8﹣4k>0,
∴k<2
综合所述,得﹣1≤k<2且k≠,
【解析】【分析】一元二次方程有两个不相等的实数根,则△=b2﹣4ac>0,结合一元二次方程的定义,求出k的取值范围.
20.【答案】(1)解:设AB=x米,由题意可得: ,
∴ ,
解得: ,
∵墙的最大可用长度为30米,且当x=5时, ,
∴ ,
答:边AB的长为15米;
(2)解:由(1)可得: ,
化简得: ,
∴ ,
∴羊圈的总面积不能为500平方米.
【解析】【分析】(1)设AB=x米,由题意可得x(80-4x)=300,求出x的值,然后根据墙的最大可用长度为30米对x的值进行取舍;
(2)由(1)可得x(80-4x)=500,求解即可判断.
21.【答案】(1)解:依题意,得 且 ,解得 且 .∵ 为非负整数,
∴
(2)解:当 时,原方程化为 ,
∴ ,
解得 ,
∴ ,
把 和 代入 ,
解得 ,
∴一次函数的解析式是 ,
把 代入 ,
解得 ,
∴反比例函数的解析式是
【解析】【分析】(1)已知一元二次方程有两个实数根,可得出k≠0且b2-4ac≥0,建立关于k的不等式,再根据k为非负整数,就可得出k的值。
(2)将k=1代入方程,再解方程,求出x的值,就可得出点A的坐标,再将k=1和点A的坐标分别代入两函数解析式,就可求得结果。
22.【答案】(1)解:∵关于x的二次方程有两个不相等的实数根,
∴ >0,
∴,
解得;
∵,
∴且;
(2)解:∵且m≠0,m为正整数,
∴m=1,
∴该方程为,
解得x1=0,x2=-1.
【解析】【分析】(1)利用一元二次方程根的判别式列出不等式求解即可;
(2)将m的值代入方程,再求解即可。
23.【答案】(1)解: x1,x2是x2+8x+m=0的两个实数根,
解得:
经检验:符合题意.
(2)解:
方程的两个根都为负数,
设
即
【解析】【分析】(1)利用一元二次方程根与系数的关系,可表示出x1+x2和x1x2,再将等式根据完全平方公式转化为(x1+x2)2-2x1x2=60,然后代入可得到关于m的方程,解方程求出m的值;
(2)利用m的值可得x1+x2和x1x2的值,由此可推出方程的两个根都为负数;设,两边同时平方,将等式的右边转化为含有x1+x2和x1x2的代数式,将其代入,可求出y的值,即可求解.
