等腰三角形的性质(1)
图片预览





文档简介
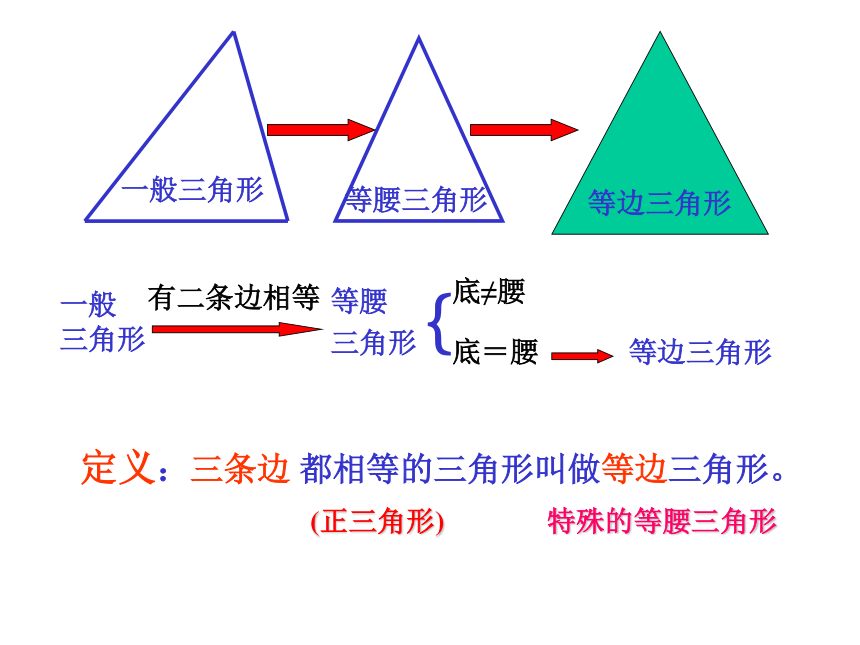
课件32张PPT。12.3.2等边三角形临海中学初二备课组 ZLQ等腰三角形等边三角形一般
三角形定义:三条边 都相等的三角形叫做等边三角形。特殊的等腰三角形一般三角形等腰
三角形等边三角形底≠腰底=腰有二条边相等{(正三角形)
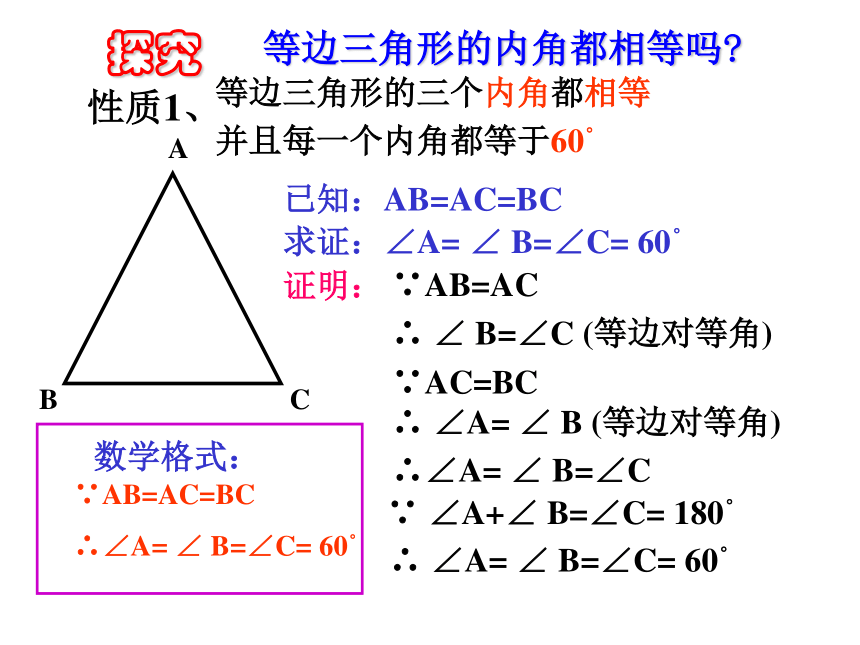
等边三角形的三个内角都相等
并且每一个内角都等于60。ABC求证:∠A= ∠ B=∠C= 60。∵AB=AC
∴ ∠ B=∠C (等边对等角)证明:数学格式:∵AB=AC=BC
∴∠A= ∠ B=∠C= 60。性质1、等边三角形的内角都相等吗?探究∵AC=BC
∴ ∠A= ∠ B (等边对等角)
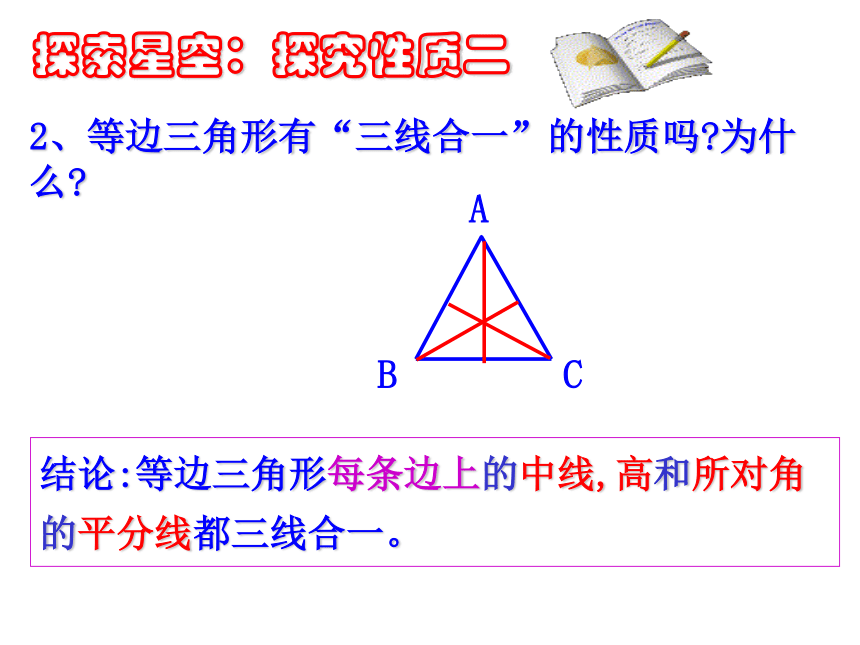
∴∠A= ∠ B=∠C已知:AB=AC=BC ∴ ∠A= ∠ B=∠C= 60。 ∵ ∠A+∠ B=∠C= 180。2、等边三角形有“三线合一”的性质吗?为什么?结论:等边三角形每条边上的中线,高和所对角的平分线都三线合一。探索星空:探究性质二3、等边三角形是轴对称图形吗?有几条对称轴?探索星空:探究性质三等边三角形的性质2.等边三角形的内角都相等,且等于60 °
3.等边三角形各边上中线,高和所对角的平分线都三线合一.4.等边三角形是轴对称图形,有三条对称轴.
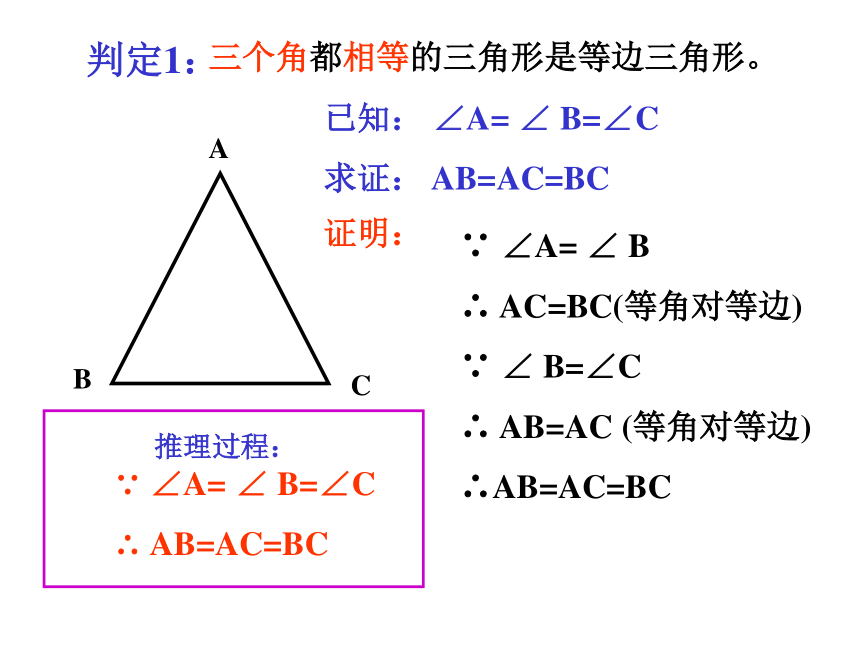
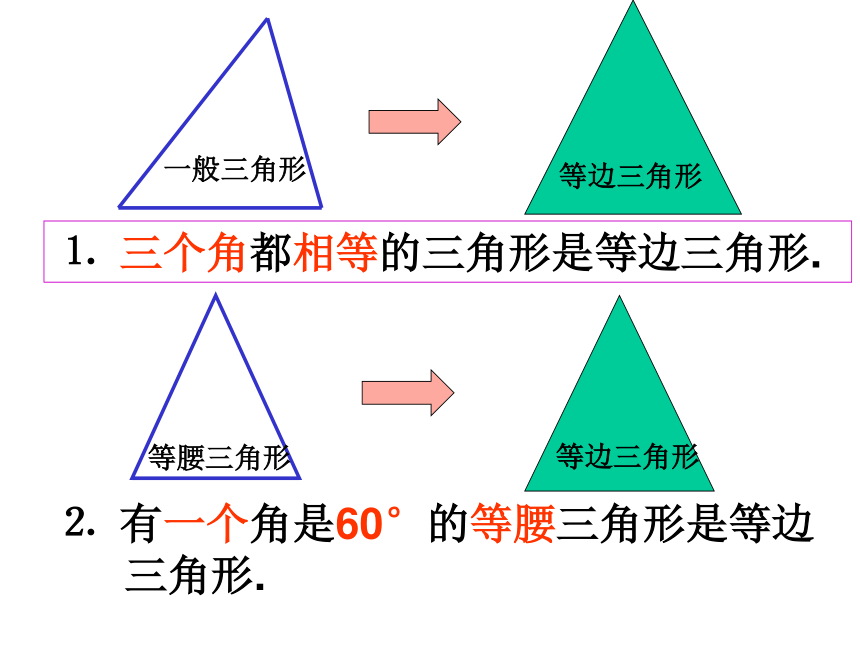
1 .三条边相等一个三角形满足什么条件就是等边三角形?思考ABC三个角都相等的三角形是等边三角形。已知: ∠A= ∠ B=∠C
求证: AB=AC=BC
∵ ∠A= ∠ B
∴ AC=BC(等角对等边)
∵ ∠ B=∠C
∴ AB=AC (等角对等边)
∴AB=AC=BC
证明:推理过程:∵ ∠A= ∠ B=∠C
∴ AB=AC=BC判定1:有一个角是60。的等腰三角形是等边三角形ABC已知: AB=AC ∠A= 60。
求证: AB=AC=BC已知: AB=AC ∠B= 60。
求证: AB=AC=BC证明:∵AB=AC ∠A= 60 。
∴∠B=∠C= (180。
-∠A)= 60。
∴∠A= ∠ B=∠C
∴AB=AC=BC
数学格式:∵AB=AC ∠A= 60。
∴ AB=AC=BC
12证明:∵AB=AC ∠B= 60。
∴∠B= ∠C= 60。
∴ ∠A=180。-∠B
- ∠C= 60。
∴∠A= ∠ B=∠C
∴ AB=AC=BC判定2:⒈ 三个角都相等的三角形是等边三角形.⒉ 有一个角是60°的等腰三角形是等边
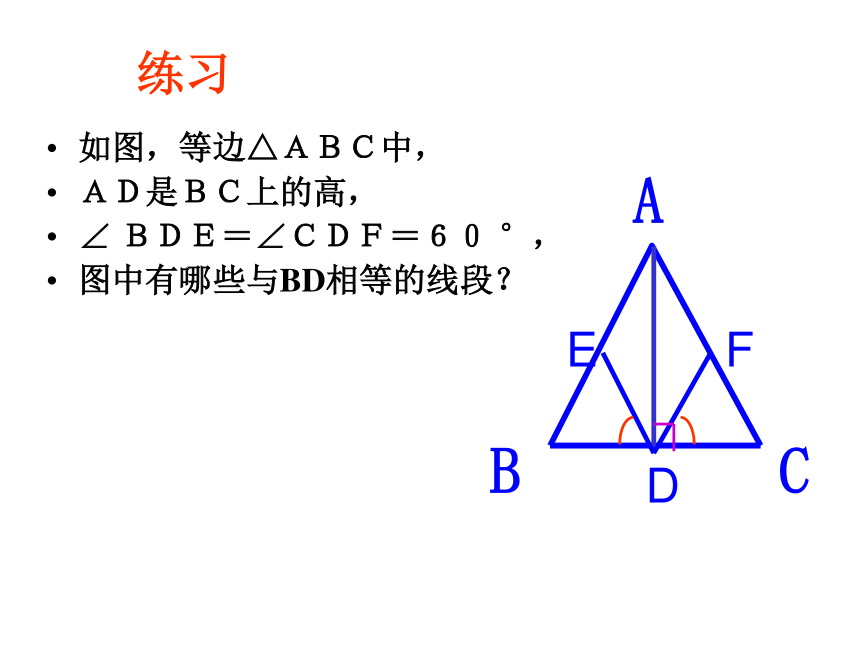
三角形.练习如图,等边△ABC中,
AD是BC上的高,
∠ BDE=∠CDF=60 °,
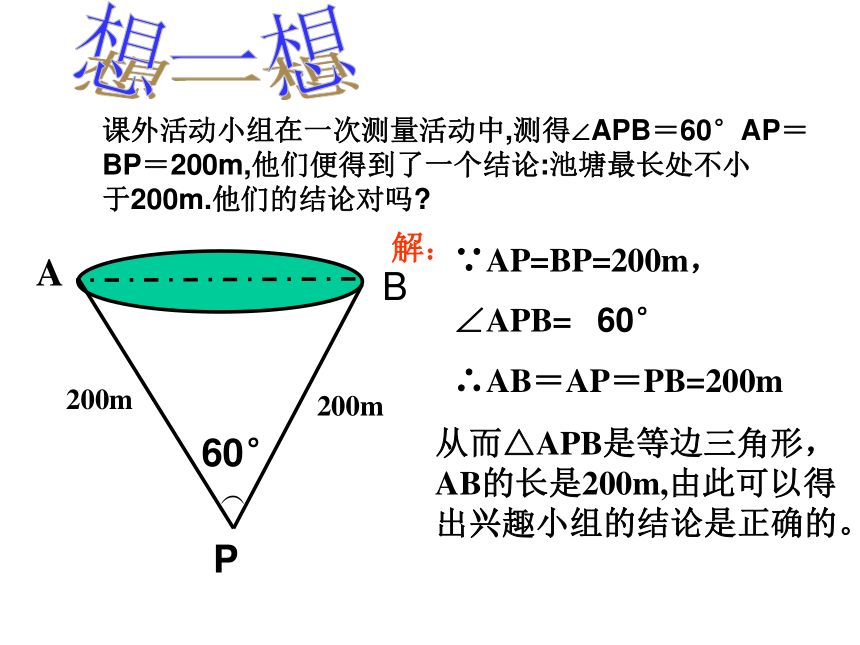
图中有哪些与BD相等的线段?想一想课外活动小组在一次测量活动中,测得∠APB=60°AP=BP=200m,他们便得到了一个结论:池塘最长处不小
于200m.他们的结论对吗?B解:∵AP=BP=200m,
∠APB= 60°
∴AB=AP=PB=200m从而△APB是等边三角形,AB的长是200m,由此可以得出兴趣小组的结论是正确的。A60°P200m200m 等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗?讨论有二条边相等1、两个底角相等
2、三线合一
3、对称轴一条1、三个角都相等
2、三线合一
3、对称轴三条有三条边相等1、定义
2、等角对等边1、定义
2、三个角都相等
3、等腰三角形有
一个角是600 1、下列四个说法中,不正确的有( )
(A)0个(B)1个(C)2个(D)3个
1、三个角都相等的三角形是等边三角形。
2、有两个角等于60°的三角形是等边三角形。
3、有一个是60°的等腰三角形是等边三角形。
4、有两个角相等的等腰三角形是等边三角形。
B火 眼 金 睛2、等边三角形的对称轴有( )
(A)1条(B)2条(C)3条(D)4条
3、等边三角形中,高、中线、角平分线共有( )
(A)3条(B)6条(C)9条(D)7条
?CA4.如图,在等边△ABC的边AB、AC
上分别截取AD=AE,△ADE是等边三
角形吗?试说明理由。ABCDE你还有其它方法
使△ADE是等边三
角形吗? △ABC是等边三角形,以下三种分 法分别得到的△ADE是等边三角形吗,为什么?
①在边AB、AC上分别截取AD=AE. 探究②作∠ADE=60,D、E分别在边AB、AC上.③过边AB上D点作DE∥BC,交边AC于E点.
ABC·P小小探索家:5.已知在等边△ABC中,如果P是△ABC所在平面上的一点,且△PAB、△PBC、△PCA都是等腰三角形,那么这样的点P的位置共有几个?试一一画出。ABCP··ABCPABCP·6.如图, △ABC为等边三角形,
∠ 1= ∠ 2= ∠ 3
(1)求∠EDF的度数.
(2)△DEF为等边三角形吗?为什么?123已知△ABC是等边三角形,D,E,F分别是各边上的一点,且AD=BE=CF.
试说明△ DEF是等边三角形.变式练一练如图,△ABD、△AEC都是等边三角形,
求证:BE=DC这是两个等边三角形,那么请移动三根火柴
,将此图变成四个等边三角形.提示:此题并不难,如果外部不能解决,那么
想想里面吧.考考你1.你能把一个等边三角形分成三个、四个、六个全等的三角形吗?若能,画出所要求的图形来,不能,则用“×”在括号内表示。( )( )( )小小探索家:2.新理念中考题
(2004·浙江)正三角形给人以“稳如泰山”的美感,它具有独特的对称性,请你用三种不同的分割方法,将图中三个正三角形分割成四个等腰三角形(在图中画出分割线,并标出必要的角的度数)。小小设计家:体会.分享请你说一说这节课的收获和体验让大家与你一起分享 ?教师寄语愿你用勤奋的汗水
浇灌智慧的花朵ABCDEFMN已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
(1)AE与CD相等吗?说明理由.
课外延伸已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
(1)AE与CD相等吗?说明理由.
证明:∵△ABD和△BCE为等边三角形∴DB=AB BC=BE∠ABD=∠EBC= 60°∴∠ABD+DBE=∠DBE+∠EBC
即∠ABE=∠DBC在△ABE和△DBC中AB=DB (已证)
∠ ABE= ∠ DBC (已证)
BE=BC (已证)∴△ABE≌△DBC∴AE=CD∴∠MAB=∠FDM{已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以
AB 、 BC为边在AC的同侧作等边△ ABD
和△ BCE,连接AE 、CD交于F,交BD于M,
交BE于N.
证明:
(2)∠AFD的度数是多少?
∵∠AMB=∠DMF ∠MAB=∠FDM
∴∠AFD=∠ABD= 60°已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
(3)BM与BN有什么关系?为什么?连接MN,△BMN是什么三角形?已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
(3)BM与BN有什么关系?为什么?连接MN,△BMN是什么三角形?证明:∵∠ ABD=∠EBC= 60° ∴∠DBE=180°-∠ABD-∠EBC=60°∴∠ABD=∠DBE在△ABM和△DBN中∠MAB=∠FDM
AB=AB
∠ABD=∠DBE
∴ △ABM≌△DBN∴ BM=BN∵ ∠DBE= 60°∴ △BMN是等边三角形{ABCDEFMN已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
(4)MN与BC平行吗?为什么?
(5)若△ABD绕B点旋转,在旋转过程中AE与CD相等吗?画出图形证明.
证明:
∵ ∠MNB =60°
又∵∠EBC= 60°
∴ ∠MNB=∠EBC
∴ MN∥BC
三角形定义:三条边 都相等的三角形叫做等边三角形。特殊的等腰三角形一般三角形等腰
三角形等边三角形底≠腰底=腰有二条边相等{(正三角形)
等边三角形的三个内角都相等
并且每一个内角都等于60。ABC求证:∠A= ∠ B=∠C= 60。∵AB=AC
∴ ∠ B=∠C (等边对等角)证明:数学格式:∵AB=AC=BC
∴∠A= ∠ B=∠C= 60。性质1、等边三角形的内角都相等吗?探究∵AC=BC
∴ ∠A= ∠ B (等边对等角)
∴∠A= ∠ B=∠C已知:AB=AC=BC ∴ ∠A= ∠ B=∠C= 60。 ∵ ∠A+∠ B=∠C= 180。2、等边三角形有“三线合一”的性质吗?为什么?结论:等边三角形每条边上的中线,高和所对角的平分线都三线合一。探索星空:探究性质二3、等边三角形是轴对称图形吗?有几条对称轴?探索星空:探究性质三等边三角形的性质2.等边三角形的内角都相等,且等于60 °
3.等边三角形各边上中线,高和所对角的平分线都三线合一.4.等边三角形是轴对称图形,有三条对称轴.
1 .三条边相等一个三角形满足什么条件就是等边三角形?思考ABC三个角都相等的三角形是等边三角形。已知: ∠A= ∠ B=∠C
求证: AB=AC=BC
∵ ∠A= ∠ B
∴ AC=BC(等角对等边)
∵ ∠ B=∠C
∴ AB=AC (等角对等边)
∴AB=AC=BC
证明:推理过程:∵ ∠A= ∠ B=∠C
∴ AB=AC=BC判定1:有一个角是60。的等腰三角形是等边三角形ABC已知: AB=AC ∠A= 60。
求证: AB=AC=BC已知: AB=AC ∠B= 60。
求证: AB=AC=BC证明:∵AB=AC ∠A= 60 。
∴∠B=∠C= (180。
-∠A)= 60。
∴∠A= ∠ B=∠C
∴AB=AC=BC
数学格式:∵AB=AC ∠A= 60。
∴ AB=AC=BC
12证明:∵AB=AC ∠B= 60。
∴∠B= ∠C= 60。
∴ ∠A=180。-∠B
- ∠C= 60。
∴∠A= ∠ B=∠C
∴ AB=AC=BC判定2:⒈ 三个角都相等的三角形是等边三角形.⒉ 有一个角是60°的等腰三角形是等边
三角形.练习如图,等边△ABC中,
AD是BC上的高,
∠ BDE=∠CDF=60 °,
图中有哪些与BD相等的线段?想一想课外活动小组在一次测量活动中,测得∠APB=60°AP=BP=200m,他们便得到了一个结论:池塘最长处不小
于200m.他们的结论对吗?B解:∵AP=BP=200m,
∠APB= 60°
∴AB=AP=PB=200m从而△APB是等边三角形,AB的长是200m,由此可以得出兴趣小组的结论是正确的。A60°P200m200m 等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗?讨论有二条边相等1、两个底角相等
2、三线合一
3、对称轴一条1、三个角都相等
2、三线合一
3、对称轴三条有三条边相等1、定义
2、等角对等边1、定义
2、三个角都相等
3、等腰三角形有
一个角是600 1、下列四个说法中,不正确的有( )
(A)0个(B)1个(C)2个(D)3个
1、三个角都相等的三角形是等边三角形。
2、有两个角等于60°的三角形是等边三角形。
3、有一个是60°的等腰三角形是等边三角形。
4、有两个角相等的等腰三角形是等边三角形。
B火 眼 金 睛2、等边三角形的对称轴有( )
(A)1条(B)2条(C)3条(D)4条
3、等边三角形中,高、中线、角平分线共有( )
(A)3条(B)6条(C)9条(D)7条
?CA4.如图,在等边△ABC的边AB、AC
上分别截取AD=AE,△ADE是等边三
角形吗?试说明理由。ABCDE你还有其它方法
使△ADE是等边三
角形吗? △ABC是等边三角形,以下三种分 法分别得到的△ADE是等边三角形吗,为什么?
①在边AB、AC上分别截取AD=AE. 探究②作∠ADE=60,D、E分别在边AB、AC上.③过边AB上D点作DE∥BC,交边AC于E点.
ABC·P小小探索家:5.已知在等边△ABC中,如果P是△ABC所在平面上的一点,且△PAB、△PBC、△PCA都是等腰三角形,那么这样的点P的位置共有几个?试一一画出。ABCP··ABCPABCP·6.如图, △ABC为等边三角形,
∠ 1= ∠ 2= ∠ 3
(1)求∠EDF的度数.
(2)△DEF为等边三角形吗?为什么?123已知△ABC是等边三角形,D,E,F分别是各边上的一点,且AD=BE=CF.
试说明△ DEF是等边三角形.变式练一练如图,△ABD、△AEC都是等边三角形,
求证:BE=DC这是两个等边三角形,那么请移动三根火柴
,将此图变成四个等边三角形.提示:此题并不难,如果外部不能解决,那么
想想里面吧.考考你1.你能把一个等边三角形分成三个、四个、六个全等的三角形吗?若能,画出所要求的图形来,不能,则用“×”在括号内表示。( )( )( )小小探索家:2.新理念中考题
(2004·浙江)正三角形给人以“稳如泰山”的美感,它具有独特的对称性,请你用三种不同的分割方法,将图中三个正三角形分割成四个等腰三角形(在图中画出分割线,并标出必要的角的度数)。小小设计家:体会.分享请你说一说这节课的收获和体验让大家与你一起分享 ?教师寄语愿你用勤奋的汗水
浇灌智慧的花朵ABCDEFMN已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
(1)AE与CD相等吗?说明理由.
课外延伸已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
(1)AE与CD相等吗?说明理由.
证明:∵△ABD和△BCE为等边三角形∴DB=AB BC=BE∠ABD=∠EBC= 60°∴∠ABD+DBE=∠DBE+∠EBC
即∠ABE=∠DBC在△ABE和△DBC中AB=DB (已证)
∠ ABE= ∠ DBC (已证)
BE=BC (已证)∴△ABE≌△DBC∴AE=CD∴∠MAB=∠FDM{已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以
AB 、 BC为边在AC的同侧作等边△ ABD
和△ BCE,连接AE 、CD交于F,交BD于M,
交BE于N.
证明:
(2)∠AFD的度数是多少?
∵∠AMB=∠DMF ∠MAB=∠FDM
∴∠AFD=∠ABD= 60°已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
(3)BM与BN有什么关系?为什么?连接MN,△BMN是什么三角形?已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
(3)BM与BN有什么关系?为什么?连接MN,△BMN是什么三角形?证明:∵∠ ABD=∠EBC= 60° ∴∠DBE=180°-∠ABD-∠EBC=60°∴∠ABD=∠DBE在△ABM和△DBN中∠MAB=∠FDM
AB=AB
∠ABD=∠DBE
∴ △ABM≌△DBN∴ BM=BN∵ ∠DBE= 60°∴ △BMN是等边三角形{ABCDEFMN已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
(4)MN与BC平行吗?为什么?
(5)若△ABD绕B点旋转,在旋转过程中AE与CD相等吗?画出图形证明.
证明:
∵ ∠MNB =60°
又∵∠EBC= 60°
∴ ∠MNB=∠EBC
∴ MN∥BC
