高中数学 人教A版(2019)必修 第一册 5.4.1 正弦函数、余弦函数的图象(共有23页ppt)
文档属性
| 名称 | 高中数学 人教A版(2019)必修 第一册 5.4.1 正弦函数、余弦函数的图象(共有23页ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 11:46:54 | ||
图片预览




文档简介
(共23张PPT)
第5章 三角函数
5.4 三角函数的图象和性质
5.4.1 正弦函数、余弦函数的图象
人教A版(2019)
教学目标
学习目标 数学素养
1.经历画正弦函数图象的过程,掌握运用“五点法”画正弦函数图象的方法; 1.数学运算素养、直观想象素养.
2.经历画余弦函数图象的过程,理解其中运用的图象变换思想. 2.直观想象素养、逻辑推理素养.
温故知新
-32°
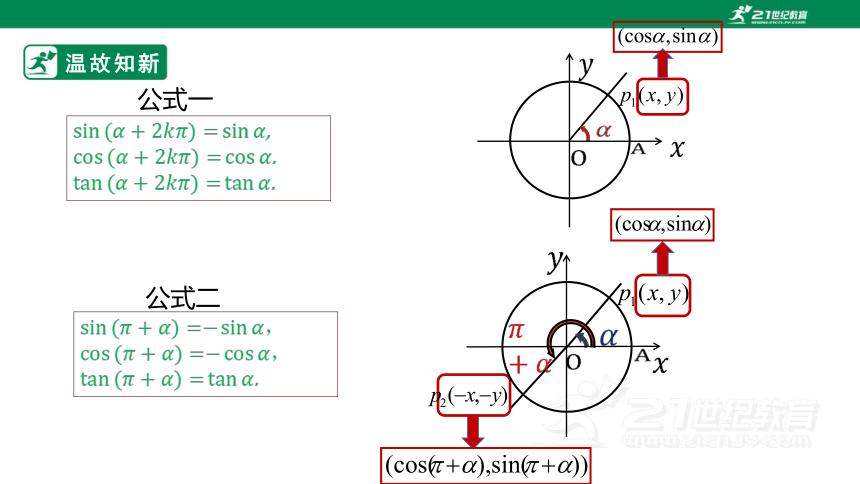
公式一
,
.
.
公式二
,
,
.
温故知新
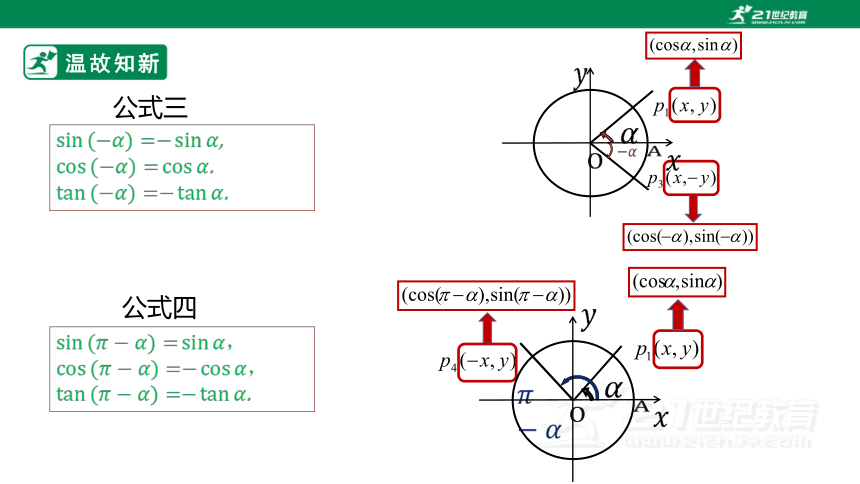
公式三
,
.
.
公式四
,
,
.
温故知新
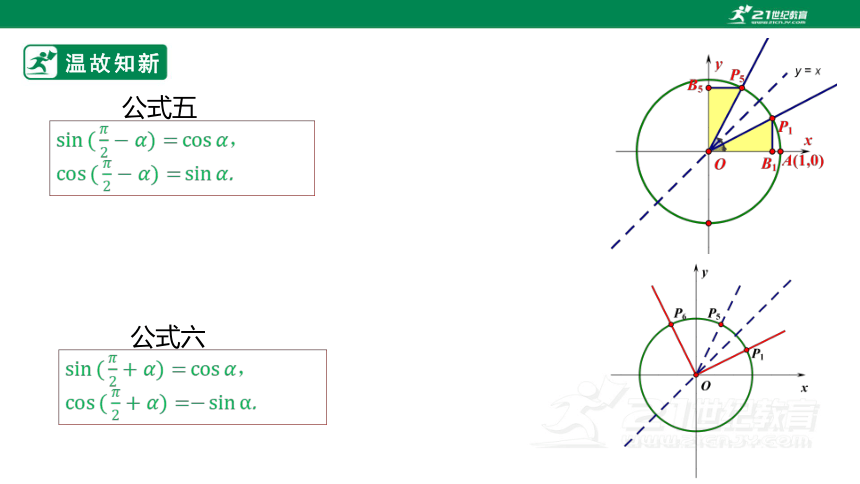
公式五
,
.
公式六
,
.
温故知新
函数定义 函数图像 函数性质
思考:我们研究指数函数、对数函数图像与性质的思路是什么呢?
我们知道,单位圆上任意一点在圆周上旋转一周就回到原来的位置,这一现象可以用公式来表示.这说明,自变量每增加(减少),正弦函数值、余弦函数值将重复出现.利用这一特性,就可以简化正弦函数、余弦函数的图象与性质的研究过程.
新知探究
下面先研究函数的图象,从画函数的图象开始.
在上任取一个值,如何利用正弦函数定义,确定正弦函数值,并画出点
如图,在直角坐标系中画出以原点为圆心的单位圆,与轴正半轴的交点为.在单位圆上,将点绕着点旋转弧度至点,根据正弦函数的定义,点的纵坐标.由此,以为横坐标,为纵坐标画点,即得到函数图象上的点.
新知探究
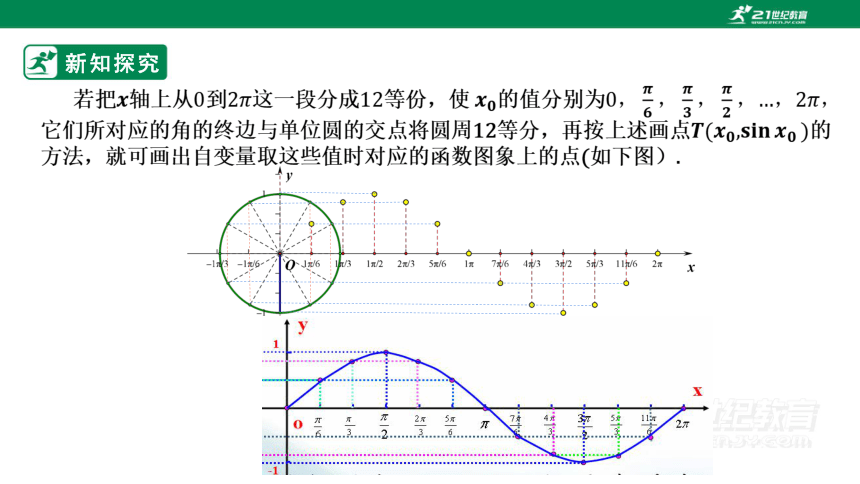
若把轴上从到这一段分成等份,使的值分别为
它们所对应的角的终边与单位圆的交点将圆周12等分,再按上述画点的方法,就可画出自变量取这些值时对应的函数图象上的点(如下图).
新知探究
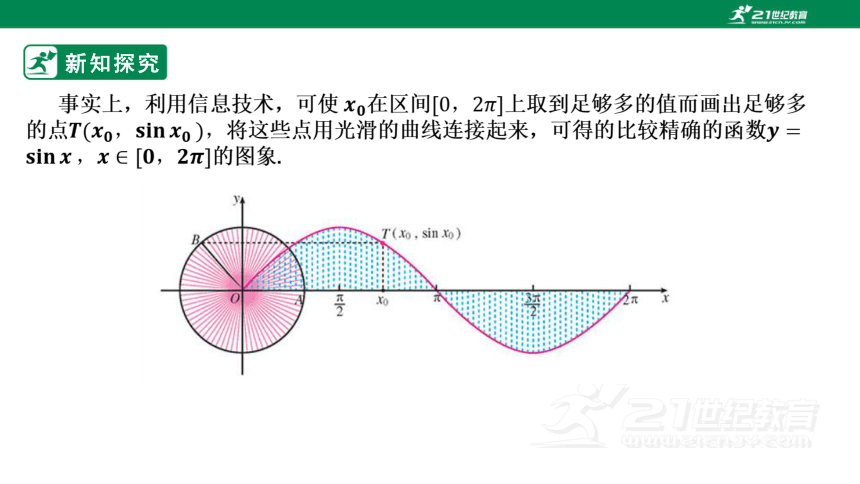
事实上,利用信息技术,可使在区间上取到足够多的值而画出足够多的点将这些点用光滑的曲线连接起来,可得的比较精确的函数的图象.
新知探究
根据函数的图象,你能想象函数的图象吗
由诱导公式一可知,函数,
的图象与,的图象形状完全一致.因此将函数,的图象不断向左、向右平移(每次移动个单位长度),就可以得到正弦函数,的图象(如下图).
正弦函数的图象叫做正弦曲线(sine curve),是一条“波浪起伏”的连续光滑曲线.
新知探究
在确定正弦函数的图象时,应抓住哪些关键点?
观察前面图象,在函数的图象上,以下五个点:
(0,0),(,1),(,0),(,-1),(,0)
在确定函数图像时起关键作用.描出这五个点,函数的图象就基本确定了.因此,在精确度要求不高时,常先找出这五个关键点,再用光滑的曲线将它们连接起来,得到正弦函数的简图.这种近似的“五点(画图)法”是非常实用的.
利用“五点法”画的步骤:
①列表确定五点坐标;
②描点;
③连线.
新知探究
你认为应该利用正弦函数和余弦函数的哪些关系,通过怎样的变换,才能正弦函数的图象变换为余弦函数的图象?
又三角函数的定义可知,正弦函数、余弦函数是一对密切关联的函数.下面我们利用这种关系,借助正弦函数的图象画出余弦函数的图象.
对于函数,由诱导公式得,
而函数的图象可以通过正弦函数,的图象向左平移个单位长度而得到.所以,将正弦函数的图象向左平移个单位长度,就得到余弦函数的图象,如图所示:
新知探究
x
y
0
1
-1
y=sinx的图象
y=cosx的图象
余弦函数,的图象叫做余弦曲线(cosine gurve).它是与正弦曲线具有相同形状的“波浪起伏”的连续光滑曲线.
类似于“五点法”画正弦函数图象,找出余弦函数再上相应的五个关键点,将它们的坐标填入下表,然后画出的简图.
x
0
-1
0
1
0
-1
新知形成
得到函数上的五个点:
y
x
O
1
-1
新知形成
解:
【例1】画出下列函数的简图:
⑴ ; ⑵.
⑴按五个关键点列表
0
0 1 0 -1 0
1 2 1 0 1
描点并用
新知形成
⑵按五个关键点列表
描点并用
0
1 0 -1 0 1
-1 0 1 0 -1
你能利用的图象,通过图象变换得到 的图象吗?同样的,利用函数[0, 2]图象,通过怎样的图象变换就能得到的图象?
将函数向上平移1个单位,得到函数的图象.将函数的图象沿x轴向下反折(作关于x轴的对称图形)得到函数的图象.
新知探求
拓展:用“五点法”画出函数的图象.
思考:
根据正弦函数、余弦函数的图象回答下列问题:
1.函数和函数的值域?
2.函数和函数的图象的对称中心、对称轴是什么?
初试身手
1.利用“五点法”画函数的简图,第三个点的坐标是
( )
A. B. C. D.
2.由函数的图象得,方程的解有( )
A.1个 B.2个 C.3个 D.4个
解:
1.根据“五点法”作图的步骤得,第三个点得坐标是,故选C.
2.由直线与函数的图象有两个交点,则方程有2个解,故选B.
C
B
课堂小结
1.正弦函数y=sinx和余弦函数y=cosx图象的画法
⑴列表描点法.
⑵图象变换法.
2.“五点法”作三角函数图象
①列表确定五点坐标;
②描点;
③连线.
作业布置
作业:P200练习 第2,4题 P213 习题5.4 第1题.
补充:
用“五点法”画出函数得简图,并回答下列问题:
⑴观察函数图象,写出满足下列条件的x的区间:①;②.
⑵若直线y=a与的图象有两个交点,求实数a的取值范围.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第5章 三角函数
5.4 三角函数的图象和性质
5.4.1 正弦函数、余弦函数的图象
人教A版(2019)
教学目标
学习目标 数学素养
1.经历画正弦函数图象的过程,掌握运用“五点法”画正弦函数图象的方法; 1.数学运算素养、直观想象素养.
2.经历画余弦函数图象的过程,理解其中运用的图象变换思想. 2.直观想象素养、逻辑推理素养.
温故知新
-32°
公式一
,
.
.
公式二
,
,
.
温故知新
公式三
,
.
.
公式四
,
,
.
温故知新
公式五
,
.
公式六
,
.
温故知新
函数定义 函数图像 函数性质
思考:我们研究指数函数、对数函数图像与性质的思路是什么呢?
我们知道,单位圆上任意一点在圆周上旋转一周就回到原来的位置,这一现象可以用公式来表示.这说明,自变量每增加(减少),正弦函数值、余弦函数值将重复出现.利用这一特性,就可以简化正弦函数、余弦函数的图象与性质的研究过程.
新知探究
下面先研究函数的图象,从画函数的图象开始.
在上任取一个值,如何利用正弦函数定义,确定正弦函数值,并画出点
如图,在直角坐标系中画出以原点为圆心的单位圆,与轴正半轴的交点为.在单位圆上,将点绕着点旋转弧度至点,根据正弦函数的定义,点的纵坐标.由此,以为横坐标,为纵坐标画点,即得到函数图象上的点.
新知探究
若把轴上从到这一段分成等份,使的值分别为
它们所对应的角的终边与单位圆的交点将圆周12等分,再按上述画点的方法,就可画出自变量取这些值时对应的函数图象上的点(如下图).
新知探究
事实上,利用信息技术,可使在区间上取到足够多的值而画出足够多的点将这些点用光滑的曲线连接起来,可得的比较精确的函数的图象.
新知探究
根据函数的图象,你能想象函数的图象吗
由诱导公式一可知,函数,
的图象与,的图象形状完全一致.因此将函数,的图象不断向左、向右平移(每次移动个单位长度),就可以得到正弦函数,的图象(如下图).
正弦函数的图象叫做正弦曲线(sine curve),是一条“波浪起伏”的连续光滑曲线.
新知探究
在确定正弦函数的图象时,应抓住哪些关键点?
观察前面图象,在函数的图象上,以下五个点:
(0,0),(,1),(,0),(,-1),(,0)
在确定函数图像时起关键作用.描出这五个点,函数的图象就基本确定了.因此,在精确度要求不高时,常先找出这五个关键点,再用光滑的曲线将它们连接起来,得到正弦函数的简图.这种近似的“五点(画图)法”是非常实用的.
利用“五点法”画的步骤:
①列表确定五点坐标;
②描点;
③连线.
新知探究
你认为应该利用正弦函数和余弦函数的哪些关系,通过怎样的变换,才能正弦函数的图象变换为余弦函数的图象?
又三角函数的定义可知,正弦函数、余弦函数是一对密切关联的函数.下面我们利用这种关系,借助正弦函数的图象画出余弦函数的图象.
对于函数,由诱导公式得,
而函数的图象可以通过正弦函数,的图象向左平移个单位长度而得到.所以,将正弦函数的图象向左平移个单位长度,就得到余弦函数的图象,如图所示:
新知探究
x
y
0
1
-1
y=sinx的图象
y=cosx的图象
余弦函数,的图象叫做余弦曲线(cosine gurve).它是与正弦曲线具有相同形状的“波浪起伏”的连续光滑曲线.
类似于“五点法”画正弦函数图象,找出余弦函数再上相应的五个关键点,将它们的坐标填入下表,然后画出的简图.
x
0
-1
0
1
0
-1
新知形成
得到函数上的五个点:
y
x
O
1
-1
新知形成
解:
【例1】画出下列函数的简图:
⑴ ; ⑵.
⑴按五个关键点列表
0
0 1 0 -1 0
1 2 1 0 1
描点并用
新知形成
⑵按五个关键点列表
描点并用
0
1 0 -1 0 1
-1 0 1 0 -1
你能利用的图象,通过图象变换得到 的图象吗?同样的,利用函数[0, 2]图象,通过怎样的图象变换就能得到的图象?
将函数向上平移1个单位,得到函数的图象.将函数的图象沿x轴向下反折(作关于x轴的对称图形)得到函数的图象.
新知探求
拓展:用“五点法”画出函数的图象.
思考:
根据正弦函数、余弦函数的图象回答下列问题:
1.函数和函数的值域?
2.函数和函数的图象的对称中心、对称轴是什么?
初试身手
1.利用“五点法”画函数的简图,第三个点的坐标是
( )
A. B. C. D.
2.由函数的图象得,方程的解有( )
A.1个 B.2个 C.3个 D.4个
解:
1.根据“五点法”作图的步骤得,第三个点得坐标是,故选C.
2.由直线与函数的图象有两个交点,则方程有2个解,故选B.
C
B
课堂小结
1.正弦函数y=sinx和余弦函数y=cosx图象的画法
⑴列表描点法.
⑵图象变换法.
2.“五点法”作三角函数图象
①列表确定五点坐标;
②描点;
③连线.
作业布置
作业:P200练习 第2,4题 P213 习题5.4 第1题.
补充:
用“五点法”画出函数得简图,并回答下列问题:
⑴观察函数图象,写出满足下列条件的x的区间:①;②.
⑵若直线y=a与的图象有两个交点,求实数a的取值范围.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
