等腰三角形的性质(2)
图片预览




文档简介
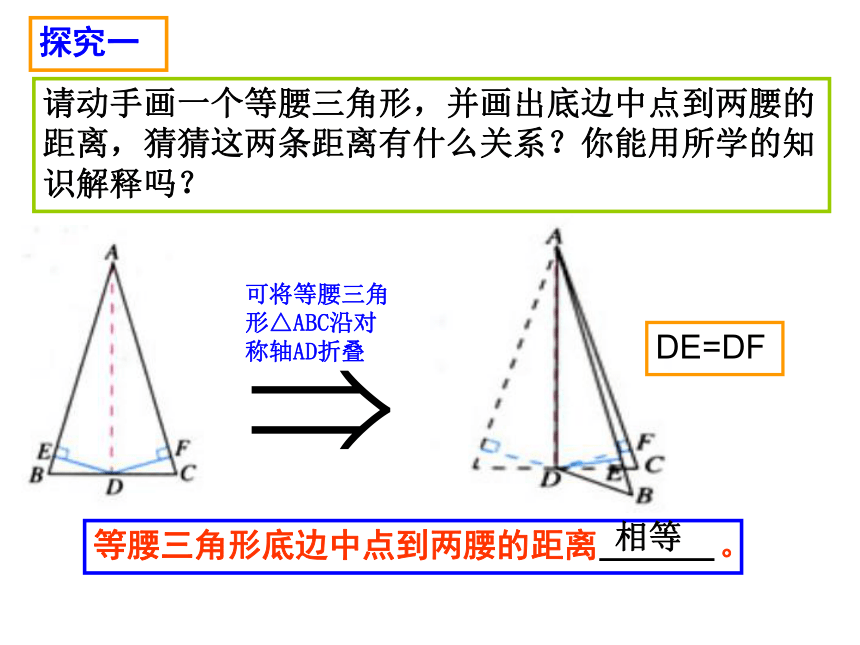
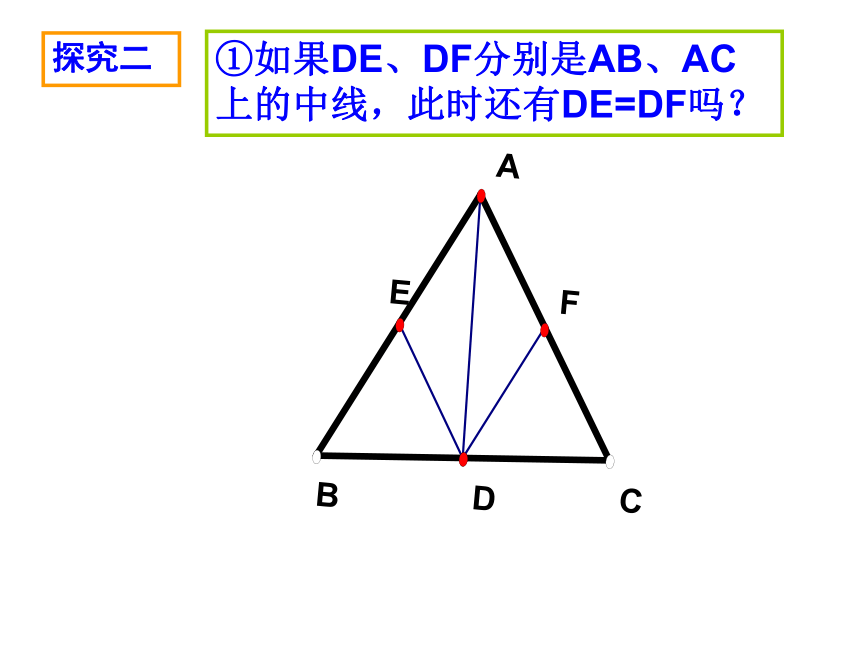
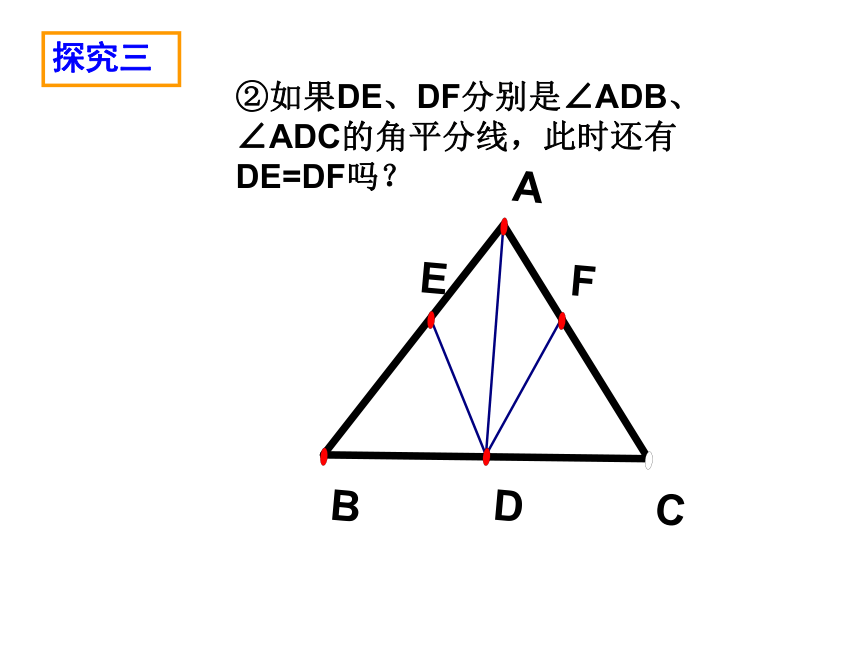
课件27张PPT。12.3.1等腰三角形(2)温中实验学校 钟凌峰探究一请动手画一个等腰三角形,并画出底边中点到两腰的距离,猜猜这两条距离有什么关系?你能用所学的知识解释吗?可将等腰三角形△ABC沿对称轴AD折叠DE=DF等腰三角形底边中点到两腰的距离 。相等①如果DE、DF分别是AB、AC上的中线,此时还有DE=DF吗?探究二②如果DE、DF分别是∠ADB、∠ADC的角平分线,此时还有DE=DF吗?探究三我们在上一节学习了等腰三角形的性质。现在你能回答我一些问题吗?
一、复习:2、等腰三角形的性质定理是什么?等腰三角形的两个底角相等。
(可以简称:等边对等角)1 、什么叫等腰三角形?有两条边相等的三角形叫等腰三角形?3、这个定理的逆命题是什么?如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。4、这个命题正确吗?你能证明吗?如果一个三角形有两个角相等,
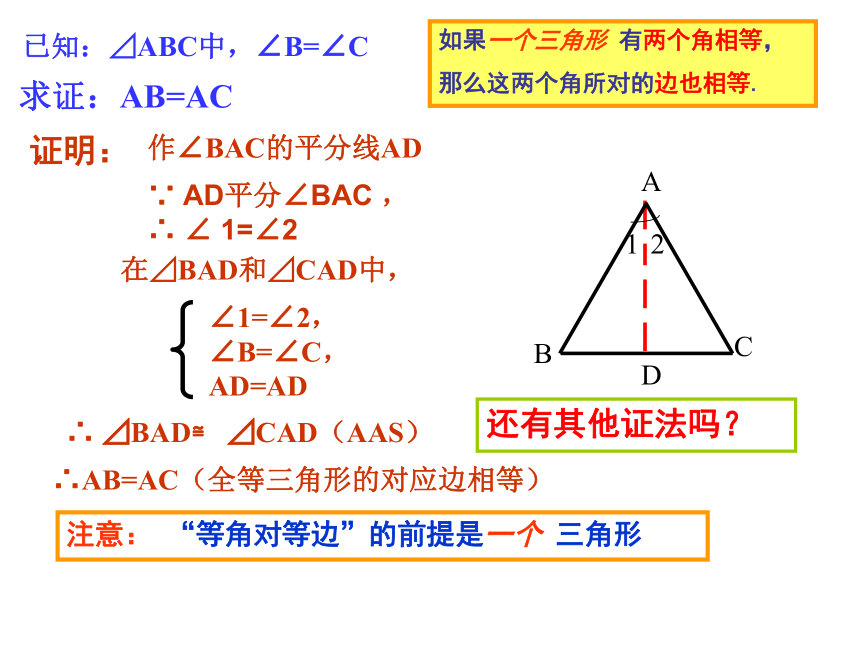
那么这两个角所对的边也相等.大胆猜测简写成”等角对等边”.等腰三角形的判定定理你能证明“等角对等边”吗?已知:⊿ABC中,∠B=∠C求证:AB=AC证明:作∠BAC的平分线AD在⊿BAD和⊿CAD中,∠1=∠2,
∠B=∠C,
AD=AD∴ ⊿BAD≌ ⊿CAD(AAS)∴AB=AC(全等三角形的对应边相等)12还有其他证法吗?∵ AD平分∠BAC ,
∴ ∠ 1=∠2如果一个三角形 有两个角相等,
那么这两个角所对的边也相等.注意: “等角对等边”的前提是一个 三角形例1:求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。求证:△ABC是等腰三角形证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等)
∠2=∠C(两直线平行,内错角相等)
∵ AD平分∠CAE
∴ ∠1=∠2,
∴∠B=∠C,
∴ △ABC是等腰三角形。练习1已知:如图,
AD ∥BC,BD平分∠ABC。
求证:AB=AD
证明: ∵ AD ∥BC
∴∠ADB=∠DBC
∵ BD平分∠ABC
∴∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD (等角对等边)已知:如图,
AD ∥BC,BD平分∠ABC。
求证:AB=AD
练习2相信你能行!已知:如图, ∠A= ∠DBC =360, ∠C=720。计算∠1和∠2,并说明图中有哪些等腰三角形?
解:∠1=720 ∠2=360等腰三角形有: ⊿ABC, ⊿ABD,⊿BCD练习3已知:如图,CD是等腰Rt△ ABC斜边上的高,找出图中有哪些等腰直角三角形。
相信你最棒!等腰直角三角形有: ⊿ABC ,⊿ACD , ⊿BCD。研究性学习如果过等腰三角形的一个顶点的直线把原三角形分成两个等腰三角形,那么原等腰三角形的顶角可能是多少度?请你画出图形,并结合图形说明理由。例2: 如图,标杆AB高为5m,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4m,绳子CD和CE要多长?选取比例尺为1:100(即以1cm代表1m) (1)作线段DE=4cm; (2)作线段DE的垂直平分线MN,与DE交于点B; (3)在MN上截取BC=2.5cm;(4)连接CD、CE,△CDE就是所求的等腰三角形。量出CD的长,就可以计算出要求的绳长,自己试一试!问题:1.如右图所示△ABC是等腰三角形,AB=AC,倘若一不留心.它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C.同学们想一想,有没有办法把原来的等腰三角形ABC重新画出来?大家试试看.ABCBC方法一:用角的相等来画.BCA方法二:用过一边中点作垂线的方法来画.BCA请你解决问题2.已知在等腰△ABC中,∠A=36°,∠ B=72°,∠C=72°,请同学们想一想,如何添一条线,将等腰△ABC分成两个等腰三角形?成功后,如何再添一条线,多得到一个等腰三角形?还可以继续吗?只要作∠ B的角平分线即可!
只要再做∠ BDC的角平分线即可!
以下步骤重复下去即可!
趣味数学如图,在△ABC中,AB=AC, ∠A=36°,你能把△ABC分成三个等腰
三角形吗?(提供两中以上不同的作图方案)ABC动手画一画 1.如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个?OD⌒CaEFH小小探索家:2.在正方形ABCD内找一点P,使△PAB、△PBC、△PCD、△PAD都是等腰三角形,这样的P点有几个?在正方形ABCD外呢?
●●●●●BACD●●●●答:在正方形内的P点有5个
在正方形外的P点有4个,如图小小探索家这些点的位置有什么特色呢?这节课你有什么 收获?小结再见
一、复习:2、等腰三角形的性质定理是什么?等腰三角形的两个底角相等。
(可以简称:等边对等角)1 、什么叫等腰三角形?有两条边相等的三角形叫等腰三角形?3、这个定理的逆命题是什么?如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。4、这个命题正确吗?你能证明吗?如果一个三角形有两个角相等,
那么这两个角所对的边也相等.大胆猜测简写成”等角对等边”.等腰三角形的判定定理你能证明“等角对等边”吗?已知:⊿ABC中,∠B=∠C求证:AB=AC证明:作∠BAC的平分线AD在⊿BAD和⊿CAD中,∠1=∠2,
∠B=∠C,
AD=AD∴ ⊿BAD≌ ⊿CAD(AAS)∴AB=AC(全等三角形的对应边相等)12还有其他证法吗?∵ AD平分∠BAC ,
∴ ∠ 1=∠2如果一个三角形 有两个角相等,
那么这两个角所对的边也相等.注意: “等角对等边”的前提是一个 三角形例1:求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。求证:△ABC是等腰三角形证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等)
∠2=∠C(两直线平行,内错角相等)
∵ AD平分∠CAE
∴ ∠1=∠2,
∴∠B=∠C,
∴ △ABC是等腰三角形。练习1已知:如图,
AD ∥BC,BD平分∠ABC。
求证:AB=AD
证明: ∵ AD ∥BC
∴∠ADB=∠DBC
∵ BD平分∠ABC
∴∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD (等角对等边)已知:如图,
AD ∥BC,BD平分∠ABC。
求证:AB=AD
练习2相信你能行!已知:如图, ∠A= ∠DBC =360, ∠C=720。计算∠1和∠2,并说明图中有哪些等腰三角形?
解:∠1=720 ∠2=360等腰三角形有: ⊿ABC, ⊿ABD,⊿BCD练习3已知:如图,CD是等腰Rt△ ABC斜边上的高,找出图中有哪些等腰直角三角形。
相信你最棒!等腰直角三角形有: ⊿ABC ,⊿ACD , ⊿BCD。研究性学习如果过等腰三角形的一个顶点的直线把原三角形分成两个等腰三角形,那么原等腰三角形的顶角可能是多少度?请你画出图形,并结合图形说明理由。例2: 如图,标杆AB高为5m,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4m,绳子CD和CE要多长?选取比例尺为1:100(即以1cm代表1m) (1)作线段DE=4cm; (2)作线段DE的垂直平分线MN,与DE交于点B; (3)在MN上截取BC=2.5cm;(4)连接CD、CE,△CDE就是所求的等腰三角形。量出CD的长,就可以计算出要求的绳长,自己试一试!问题:1.如右图所示△ABC是等腰三角形,AB=AC,倘若一不留心.它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C.同学们想一想,有没有办法把原来的等腰三角形ABC重新画出来?大家试试看.ABCBC方法一:用角的相等来画.BCA方法二:用过一边中点作垂线的方法来画.BCA请你解决问题2.已知在等腰△ABC中,∠A=36°,∠ B=72°,∠C=72°,请同学们想一想,如何添一条线,将等腰△ABC分成两个等腰三角形?成功后,如何再添一条线,多得到一个等腰三角形?还可以继续吗?只要作∠ B的角平分线即可!
只要再做∠ BDC的角平分线即可!
以下步骤重复下去即可!
趣味数学如图,在△ABC中,AB=AC, ∠A=36°,你能把△ABC分成三个等腰
三角形吗?(提供两中以上不同的作图方案)ABC动手画一画 1.如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个?OD⌒CaEFH小小探索家:2.在正方形ABCD内找一点P,使△PAB、△PBC、△PCD、△PAD都是等腰三角形,这样的P点有几个?在正方形ABCD外呢?
●●●●●BACD●●●●答:在正方形内的P点有5个
在正方形外的P点有4个,如图小小探索家这些点的位置有什么特色呢?这节课你有什么 收获?小结再见
