1.1 探索勾股定理 第2课时课件 (共14张PPT)北师大版八年级上册数学
文档属性
| 名称 | 1.1 探索勾股定理 第2课时课件 (共14张PPT)北师大版八年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 993.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
1 探索勾股定理 第2课时
第一章 勾股定理
1.能用勾股定理解决一些实际问题.
2.会用拼图的方法验证勾股定理,体验数形结合的好处.
◎重点:勾股定理的验证及其应用.
我们已经通过数格子的方法发现了勾股定理,那么如何验证勾股定理呢 ?据不完全统计,验证勾股定理的方法有500多种,你有自己的方法吗?下面请大家画四个全等的直角三角形,并把它们剪下来,用这四个直角三角形拼一拼、摆一摆,看看能否得到一个以斜边为边长的正方形.
勾股定理的证明
阅读教材本课时“做一做”至“例题”前面的内容,填空:
已知直角三角形的两边可以求出 第三边 ,用勾股定理可以解决实际问题.
·导学建议·
利用拼图的方法验证勾股定理,是我国古代数学家的一大贡献.在拼图过程中,鼓励学生大胆联想.
1.如图,有一个水池,截面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,若把这根芦苇拉向水池边的中点,它的顶端恰好到达池边的水面,则水的深度是 ( D )
A.8尺 B.10尺 C.13尺 D.12尺
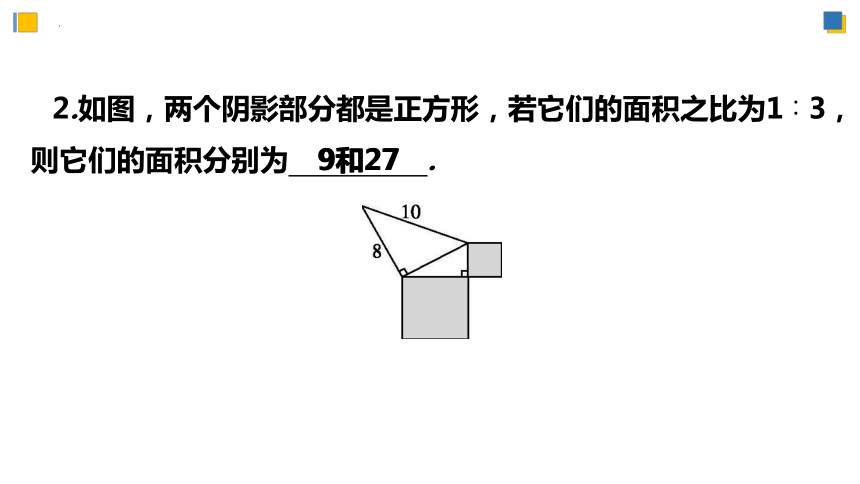
2.如图,两个阴影部分都是正方形,若它们的面积之比为1∶3,则它们的面积分别为 9和27 .
9和27
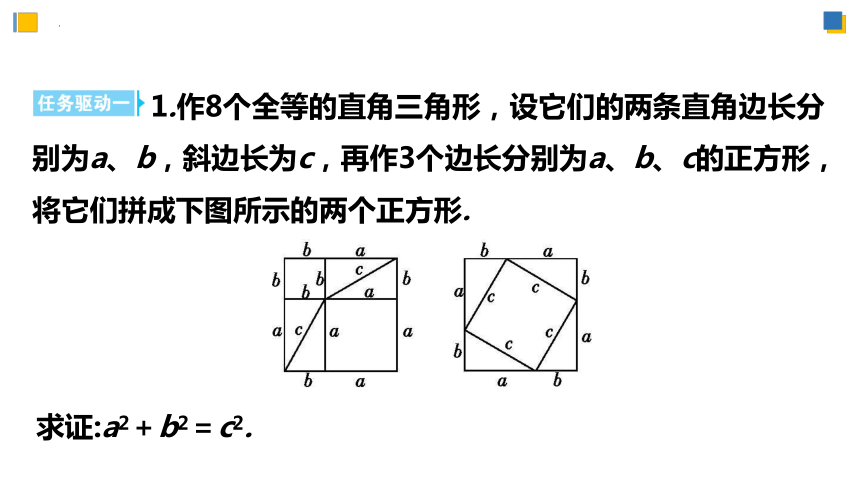
1.作8个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c,再作3个边长分别为a、b、c的正方形,将它们拼成下图所示的两个正方形.
求证:a2+b2=c2.
证明:由图易知,这两个正方形的边长都是a+b,所以它们的面积相等.左边的正方形面积可表示为a2+b2+ab×4,右边的正方形面积可表示为c2+ab×4.因为a2+b2+ab×4=c2+ab×4,所以a2+b2=c2.
方法归纳交流 根据拼图,通过对拼接图形的面积的不同表示,建立相等关系,从而验证勾股定理.
变式演练
用四个全等的直角三角形拼成了一个如图所示的图形,其中a表示较短的直角边,b表示较长的直角边,c表示斜边,你能用这个图形证明勾股定理吗?
解:能验证,理由如下:根据题意得4×ab+(b-a)2=c2,整理得a2+b2=c2.
2.如图,这是某公园中的荷花池,现要测量此荷花池两旁A、B两棵树间的距离(我们不能直接量得).请你根据所学知识,以卷尺和测角仪为测量工具设计一种测量方案.要求:
(1)画出你设计的测量平面图.
(2)简述测量方法,并写出测量的数据(长度用a,b,c…表示,角度用α,β,γ…表示).
(3)根据你测量的数据,计算A,B两棵树间的距离.
解:(1)如图所示.
(2)在点A处测得∠BAE=90°,并在射线AE上的适当位置取点C,量出AC=a,CB=b.
(3)根据测量的数据AC=a,CB=b,
由勾股定理,得AB2=BC2-AC2=b2-a2.
(3)根据测量的数据AC=a,CB=b,
由勾股定理,得AB2=BC2-AC2=b2-a2.
变式演练 如图,隔湖有两点A、B,为了测得A、B两点间的距离,在与AB方向成直角的BC方向上任取一点C,测得CA=50 m,CB=40 m,那么A、B两点间的距离是 30 m.
1 探索勾股定理 第2课时
第一章 勾股定理
1.能用勾股定理解决一些实际问题.
2.会用拼图的方法验证勾股定理,体验数形结合的好处.
◎重点:勾股定理的验证及其应用.
我们已经通过数格子的方法发现了勾股定理,那么如何验证勾股定理呢 ?据不完全统计,验证勾股定理的方法有500多种,你有自己的方法吗?下面请大家画四个全等的直角三角形,并把它们剪下来,用这四个直角三角形拼一拼、摆一摆,看看能否得到一个以斜边为边长的正方形.
勾股定理的证明
阅读教材本课时“做一做”至“例题”前面的内容,填空:
已知直角三角形的两边可以求出 第三边 ,用勾股定理可以解决实际问题.
·导学建议·
利用拼图的方法验证勾股定理,是我国古代数学家的一大贡献.在拼图过程中,鼓励学生大胆联想.
1.如图,有一个水池,截面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,若把这根芦苇拉向水池边的中点,它的顶端恰好到达池边的水面,则水的深度是 ( D )
A.8尺 B.10尺 C.13尺 D.12尺
2.如图,两个阴影部分都是正方形,若它们的面积之比为1∶3,则它们的面积分别为 9和27 .
9和27
1.作8个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c,再作3个边长分别为a、b、c的正方形,将它们拼成下图所示的两个正方形.
求证:a2+b2=c2.
证明:由图易知,这两个正方形的边长都是a+b,所以它们的面积相等.左边的正方形面积可表示为a2+b2+ab×4,右边的正方形面积可表示为c2+ab×4.因为a2+b2+ab×4=c2+ab×4,所以a2+b2=c2.
方法归纳交流 根据拼图,通过对拼接图形的面积的不同表示,建立相等关系,从而验证勾股定理.
变式演练
用四个全等的直角三角形拼成了一个如图所示的图形,其中a表示较短的直角边,b表示较长的直角边,c表示斜边,你能用这个图形证明勾股定理吗?
解:能验证,理由如下:根据题意得4×ab+(b-a)2=c2,整理得a2+b2=c2.
2.如图,这是某公园中的荷花池,现要测量此荷花池两旁A、B两棵树间的距离(我们不能直接量得).请你根据所学知识,以卷尺和测角仪为测量工具设计一种测量方案.要求:
(1)画出你设计的测量平面图.
(2)简述测量方法,并写出测量的数据(长度用a,b,c…表示,角度用α,β,γ…表示).
(3)根据你测量的数据,计算A,B两棵树间的距离.
解:(1)如图所示.
(2)在点A处测得∠BAE=90°,并在射线AE上的适当位置取点C,量出AC=a,CB=b.
(3)根据测量的数据AC=a,CB=b,
由勾股定理,得AB2=BC2-AC2=b2-a2.
(3)根据测量的数据AC=a,CB=b,
由勾股定理,得AB2=BC2-AC2=b2-a2.
变式演练 如图,隔湖有两点A、B,为了测得A、B两点间的距离,在与AB方向成直角的BC方向上任取一点C,测得CA=50 m,CB=40 m,那么A、B两点间的距离是 30 m.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
