3.2解一元一次方程 合并同类课件(共37张PPT) 人教版七年级数学上册
文档属性
| 名称 | 3.2解一元一次方程 合并同类课件(共37张PPT) 人教版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 14:25:16 | ||
图片预览







文档简介
(共37张PPT)
3.2 解一元一次方程(一)
第1课时
配套人教版
学习目标
掌握合并同类项的方法,能够熟练解形如 的方程
理解解方程的过程就是使方程逐步转化为 的形式,体现化归思想
进一步利用列方程的方法解决实际问题,体会建立数学模型的思想
通过探究实际问题与一元一次方程的关系,进一步体会利用一元一次方程解决问题的基本过程,感受数学的应用价值,提高解决问题的能力.
重点
合并同类项
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
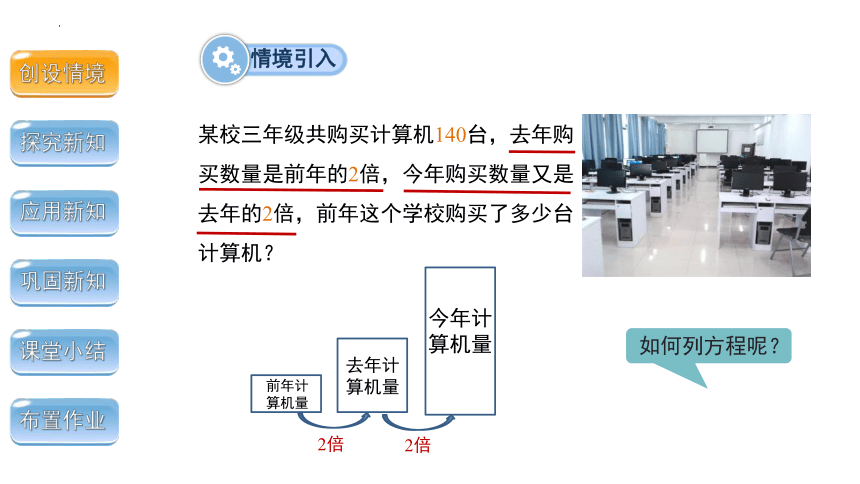
情境引入
如何列方程呢?
某校三年级共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍,前年这个学校购买了多少台计算机?
2倍
前年计
算机量
去年计
算机量
2倍
今年计算机量
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
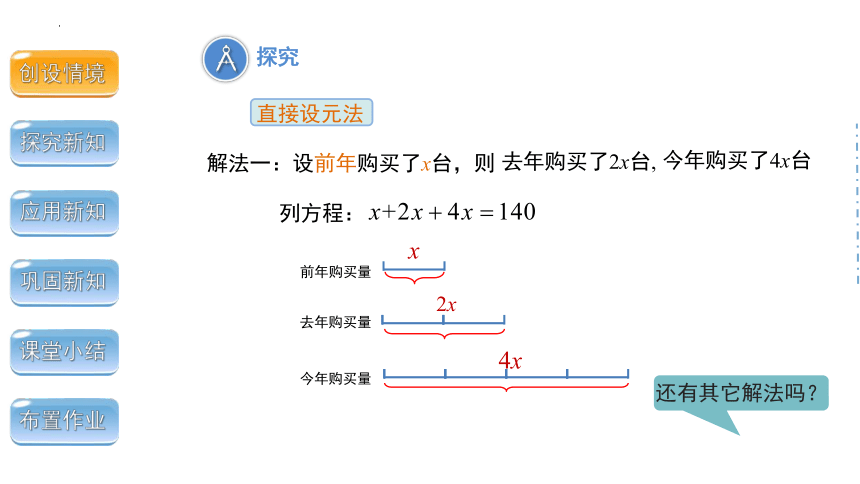
直接设元法
探究
解法一:设前年购买了x台,则
去年购买了2x台,
今年购买了4x台
列方程:
还有其它解法吗?
前年购买量
x
去年购买量
2x
今年购买量
4x
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
探究
解法二:设去年购买了x台,则
今年购买了2x台
前年购买了 x台,
列方程:
还有其它解法吗?
间接设元法
去年购买量
x
前年购买量
今年购买量
解法三:设今年购买了x台,则
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
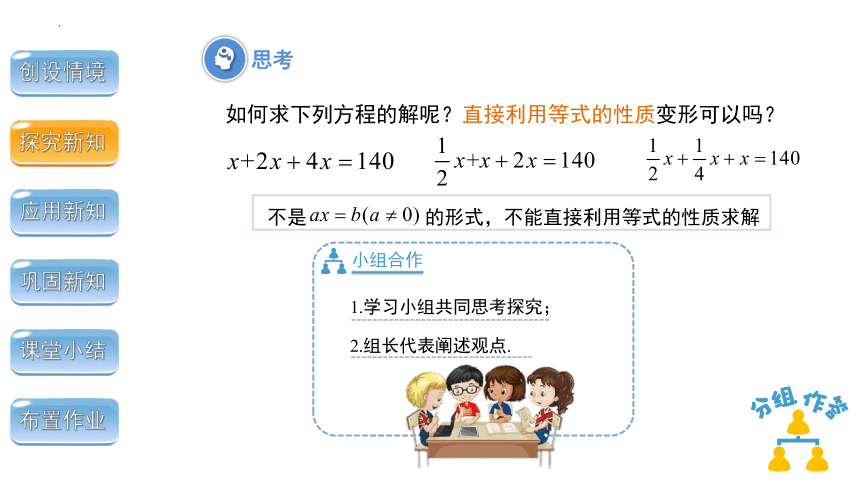
小组合作
1.学习小组共同思考探究;
2.组长代表阐述观点.
如何求下列方程的解呢?直接利用等式的性质变形可以吗?
思考
不是 的形式,不能直接利用等式的性质求解
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
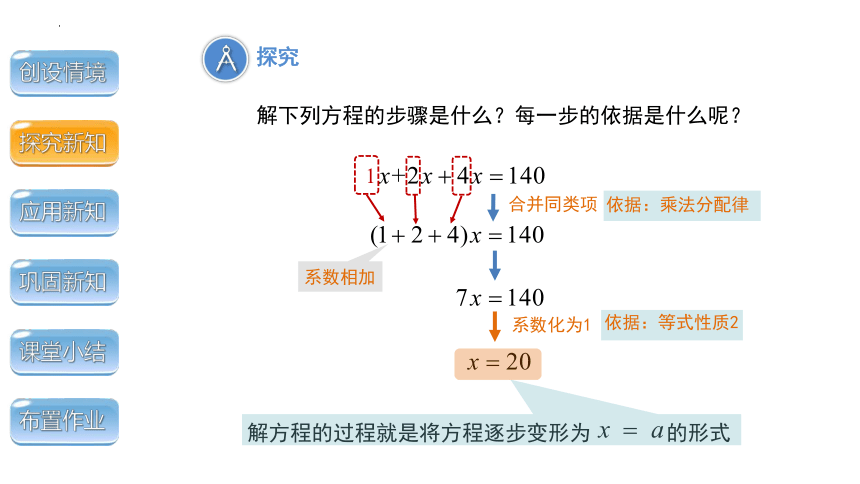
依据:乘法分配律
系数化为1
依据:等式性质2
解下列方程的步骤是什么?每一步的依据是什么呢?
探究
合并同类项
1
解方程的过程就是将方程逐步变形为 的形式
系数相加
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
归纳
解应用题的一般步骤:
审 —审题,明确关键信息
设 —设合适的未知量为x
列 —依据等量关系列方程
解 —采取最优步骤方案求解
验 —检验答案是否符合实际问题
答 —勿忘答题
合并同类项,得
系数化为1,得
解:设前年购买了x台,则
去年购买了2x台,
今年购买了4x台,
答:前年购买了20台电脑.
解法一
解法二、解法三你能完成吗?答案与解法一,一致吗?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
A.
合并同类项时,要注意不能丢掉系数中的负号.
几个常数项也可以合并为一项.
做一做
将 合并同类项,正确的是( )
B.
C.
D.
解析:
合并同类项,得
B
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
(1)
解下列方程
例1
(1)系数化为1时,在方程两边同时除以未知数的系数(或者乘以未知数系数的倒数)
(2)如果方程中项的系数是带分数的话,一般写成假分数
系数化为1,得
(1)
解:
合并同类项,得
合并同类项时,注意不能丢掉负号
探究新知
解下列方程
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例1
(2)
合并同类项要注意每项系数的符号,合并时要将各项的系数进行相加
系数化为1, 得
(2)
解:
合并同类项,得
不能丢掉负号
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
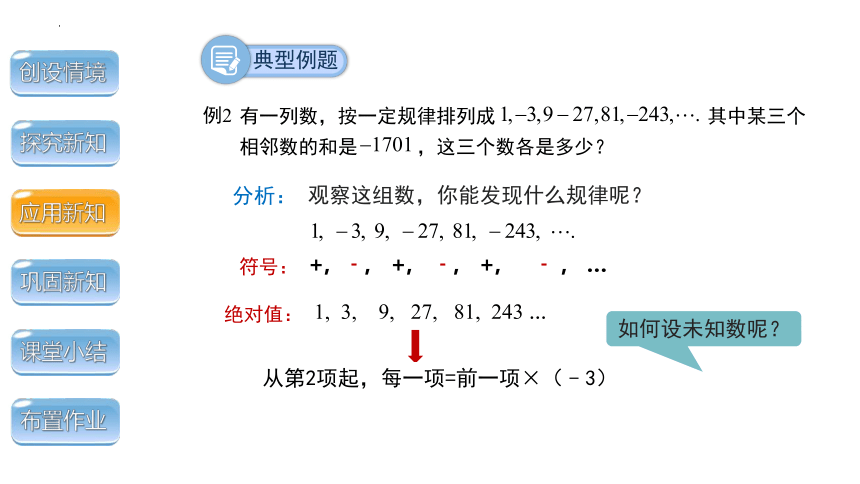
例2
有一列数,按一定规律排列成 其中某三个
相邻数的和是 ,这三个数各是多少?
观察这组数,你能发现什么规律呢?
分析:
符号:
+, ﹣, +, ﹣, +, ﹣ , …
绝对值:
1, 3, 9, 27, 81, 243 …
从第2项起,每一项=前一项×(﹣3)
如何设未知数呢?
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例2
有一列数,按一定规律排列成 其中某三个
相邻数的和是 ,这三个数各是多少?
解法1:设三个相邻数中的第1个为x,
合并同类项,得
系数化为1,得
所以 ,
第3个为9x.
则第2个为 ,
答: 这三个数分别是
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例2
有一列数,按一定规律排列成 其中某三个
相邻数的和是 ,这三个数各是多少?
第2个数为x,
解法2:
第1个数为 ,
第3个数为 ,则
所以 ,
答: 这三个数分别是
还有其他设法吗?
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
解下列方程.
(1)
(2)
(3)
(1)
解:
合并同类项,得
系数化为1,得
(2)
解:
合并同类项,得
系数化为1,得
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
解下列方程.
(1)
(2)
(3)
(3)
解:
合并同类项,得
系数化为1,得
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
列方程解应用题的一般步骤:
用合并同类项解方程:
审、设、列、解、验、答
2、几个常数项也可以合并同类项
3、逐步使方程变形为 x=a 的形式
合并同类项
1、系数相加,未知数不变(注意系数中的负号)
再见
3.2 解一元一次方程(一)
第2课时
配套人教版
学习目标
掌握移项的定义,能够熟练利用移项解简单的方程;
理解解方程的过程就是使方程逐步转化为 的形式,体会化归思想 ;
进一步利用列方程的方法解决实际问题,体会建立数学模型的思想;
通过探究实际问题与一元一次方程的关系,进一步体会利用一元方程解决问题的基本过程,感受数学的应用价值,提高分析、解决问题的能力.
重点
移
项
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
情境引入
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本,如果每人分4本,则还缺25本,这个班有多少学生?
分析:设这个班有x个学生,则书总量为:
分法一:
分法二:
等量关系:
分法一书总量 = 分法二书总量
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
探究
合并同类项
系数化为1
将方程如何变形,才可以合并同类项呢?
可以直接合并同类项吗?上节课是如何处理的?
含x的项全部在等号的左边,常数项全部在等号的右边
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
目的:右边的4x变号后移到了左边
目的:左边的20变号后移到了右边
等式两边减去4x
等式两边减去20
整理
每一步变形都要保证变形后的方程与原方程的解相同
依据:等式性质1
依据:等式性质1
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
把左边的常数项变号后,移到右边
把右边的4x变号后,移到左边
把等式一边的某项变号后移到另一边,叫做移项.
移项:
移项的作用:
让方程更加接近“x=a”.
移项的依据:
等式性质1.
(1)移项要变号
(2)一般把含有x的项移到等号的左边,常数项移到等号的右边
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
做一做
方程 ,移项正确的是( )
A.
B.
C.
D.
B
移项,得
解析:
未变号
常数项应移到右边
-7未变号
探究新知
解下列方程
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
(1)
(2)
例3
(先移项再合并同类项)
(1)
解:
移项,得
合并同类项,得
系数化为1,得
探究新知
解下列方程
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例3
(1)
(2)
合并同类项,得
系数化为1,得
(2)
解:
移项,得
(先移项再合并同类项)
探究新知
解下列方程
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例3
(3)
移项,得
系数化为1,得
合并同类项,得
(3)
合并同类项,得
解:
小结:
(1)当方程两边各有可以合并的同类项时,可以根据情况先合并同类项再移项,减少出错.
(2)移项时注意变号.
(先合并同类项再移项)
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例4
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200t ;如用新工艺,则废水排量比环保限制的最大量少100t,新、旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?
分析: 旧工艺废水排量 = 环保限制的最大量 + 200,①
新工艺废水排量 = 环保限制的最大量 – 100,②
新工艺废水排量 :旧工艺废水排量 = 2 : 5. ③
如何设未知数呢?
直接设法:
间接设法:
设新、旧工艺的废水排量分别为 2x t 和 5x t.
方法1:设环保限制的最大量为 x t
间接设法需要引入x
方法2:设新工艺废水排量为 x t
方法3:设旧工艺废水排量为 x t
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
解法一:设新、旧工艺的废水排量分别为 2x t 和 5x t.
根据废水排量与环保限制最大量之间的关系,得
5x – 200 = 2x + 100.
移项,得 5x – 2x = 100 + 200.
合并同类项,得 3x = 300.
系数化为 1,得 x = 100.
所以 2x = 200,5x = 500.
答:新、旧工艺产生的废水排量分别为 200 t 和 500 t.
旧工艺废水排量 = 环保限制的最大量 + 200,①
新工艺废水排量 = 环保限制的最大量 – 100,②
新工艺废水排量 :旧工艺废水排量 = 2 : 5. ③
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
解法二:设环保限制的最大量为 a t,
根据条件①,得旧工艺废水排量为(a + 200)t,
根据条件②,得新工艺废水排量为(a – 100)t,
根据条件③,可列方程
(a – 100):(a + 200)= 2 : 5.
旧工艺废水排量 = 环保限制的最大量 + 200,①
新工艺废水排量 = 环保限制的最大量 – 100,②
新工艺废水排量 :旧工艺废水排量 = 2 : 5. ③
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
小结:
(1)未知数不同,等量关系不同,则所列方程就不同
(2)所的结果是相同的
解法三:设新工艺废水排量为 b t,
根据条件②,得环保限制的最大量为(b + 100)t,
根据条件①,得旧工艺废水排量为(b + 100 + 200)t,
根据条件③,可列方程
b :(b + 100 + 200)= 2 : 5.
旧工艺废水排量 = 环保限制的最大量 + 200,①
新工艺废水排量 = 环保限制的最大量 – 100,②
新工艺废水排量 :旧工艺废水排量 = 2 : 5. ③
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
解下列方程
(1)
(2)
(1)
解:
移项,得
合并同类项,得
系数化为1,得
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
(1)
(2)
解下列方程
(2)
解:
移项,得
合并同类项,得
系数化为1,得
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
在一张普通的月历中,相邻三行里同一列的三个日期数之和能否为30?如果能,这三个数分别是多少?
解:
设这三个数分别是 x,x+7,x+14.
根据相邻三行里同一列的三个日期数之和为30,列出方程
x+x+7+x+14=30.
解方程,得 x=3.
所以这三个数是3,10,17.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
解方程技巧:
移项:移项要变号
项数较多时,先合并同类项再移项
移项的依据:等式性质1
把等号一边的某项变号后移到另一边,叫做移项
移项后,方程的解不会改变
移项
通常把未知数移到等号的左边,把常数项移到右边
再见
3.2 解一元一次方程(一)
第1课时
配套人教版
学习目标
掌握合并同类项的方法,能够熟练解形如 的方程
理解解方程的过程就是使方程逐步转化为 的形式,体现化归思想
进一步利用列方程的方法解决实际问题,体会建立数学模型的思想
通过探究实际问题与一元一次方程的关系,进一步体会利用一元一次方程解决问题的基本过程,感受数学的应用价值,提高解决问题的能力.
重点
合并同类项
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
情境引入
如何列方程呢?
某校三年级共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍,前年这个学校购买了多少台计算机?
2倍
前年计
算机量
去年计
算机量
2倍
今年计算机量
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
直接设元法
探究
解法一:设前年购买了x台,则
去年购买了2x台,
今年购买了4x台
列方程:
还有其它解法吗?
前年购买量
x
去年购买量
2x
今年购买量
4x
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
探究
解法二:设去年购买了x台,则
今年购买了2x台
前年购买了 x台,
列方程:
还有其它解法吗?
间接设元法
去年购买量
x
前年购买量
今年购买量
解法三:设今年购买了x台,则
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
小组合作
1.学习小组共同思考探究;
2.组长代表阐述观点.
如何求下列方程的解呢?直接利用等式的性质变形可以吗?
思考
不是 的形式,不能直接利用等式的性质求解
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
依据:乘法分配律
系数化为1
依据:等式性质2
解下列方程的步骤是什么?每一步的依据是什么呢?
探究
合并同类项
1
解方程的过程就是将方程逐步变形为 的形式
系数相加
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
归纳
解应用题的一般步骤:
审 —审题,明确关键信息
设 —设合适的未知量为x
列 —依据等量关系列方程
解 —采取最优步骤方案求解
验 —检验答案是否符合实际问题
答 —勿忘答题
合并同类项,得
系数化为1,得
解:设前年购买了x台,则
去年购买了2x台,
今年购买了4x台,
答:前年购买了20台电脑.
解法一
解法二、解法三你能完成吗?答案与解法一,一致吗?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
A.
合并同类项时,要注意不能丢掉系数中的负号.
几个常数项也可以合并为一项.
做一做
将 合并同类项,正确的是( )
B.
C.
D.
解析:
合并同类项,得
B
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
(1)
解下列方程
例1
(1)系数化为1时,在方程两边同时除以未知数的系数(或者乘以未知数系数的倒数)
(2)如果方程中项的系数是带分数的话,一般写成假分数
系数化为1,得
(1)
解:
合并同类项,得
合并同类项时,注意不能丢掉负号
探究新知
解下列方程
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例1
(2)
合并同类项要注意每项系数的符号,合并时要将各项的系数进行相加
系数化为1, 得
(2)
解:
合并同类项,得
不能丢掉负号
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例2
有一列数,按一定规律排列成 其中某三个
相邻数的和是 ,这三个数各是多少?
观察这组数,你能发现什么规律呢?
分析:
符号:
+, ﹣, +, ﹣, +, ﹣ , …
绝对值:
1, 3, 9, 27, 81, 243 …
从第2项起,每一项=前一项×(﹣3)
如何设未知数呢?
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例2
有一列数,按一定规律排列成 其中某三个
相邻数的和是 ,这三个数各是多少?
解法1:设三个相邻数中的第1个为x,
合并同类项,得
系数化为1,得
所以 ,
第3个为9x.
则第2个为 ,
答: 这三个数分别是
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例2
有一列数,按一定规律排列成 其中某三个
相邻数的和是 ,这三个数各是多少?
第2个数为x,
解法2:
第1个数为 ,
第3个数为 ,则
所以 ,
答: 这三个数分别是
还有其他设法吗?
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
解下列方程.
(1)
(2)
(3)
(1)
解:
合并同类项,得
系数化为1,得
(2)
解:
合并同类项,得
系数化为1,得
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
解下列方程.
(1)
(2)
(3)
(3)
解:
合并同类项,得
系数化为1,得
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
列方程解应用题的一般步骤:
用合并同类项解方程:
审、设、列、解、验、答
2、几个常数项也可以合并同类项
3、逐步使方程变形为 x=a 的形式
合并同类项
1、系数相加,未知数不变(注意系数中的负号)
再见
3.2 解一元一次方程(一)
第2课时
配套人教版
学习目标
掌握移项的定义,能够熟练利用移项解简单的方程;
理解解方程的过程就是使方程逐步转化为 的形式,体会化归思想 ;
进一步利用列方程的方法解决实际问题,体会建立数学模型的思想;
通过探究实际问题与一元一次方程的关系,进一步体会利用一元方程解决问题的基本过程,感受数学的应用价值,提高分析、解决问题的能力.
重点
移
项
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
情境引入
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本,如果每人分4本,则还缺25本,这个班有多少学生?
分析:设这个班有x个学生,则书总量为:
分法一:
分法二:
等量关系:
分法一书总量 = 分法二书总量
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
探究
合并同类项
系数化为1
将方程如何变形,才可以合并同类项呢?
可以直接合并同类项吗?上节课是如何处理的?
含x的项全部在等号的左边,常数项全部在等号的右边
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
目的:右边的4x变号后移到了左边
目的:左边的20变号后移到了右边
等式两边减去4x
等式两边减去20
整理
每一步变形都要保证变形后的方程与原方程的解相同
依据:等式性质1
依据:等式性质1
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
把左边的常数项变号后,移到右边
把右边的4x变号后,移到左边
把等式一边的某项变号后移到另一边,叫做移项.
移项:
移项的作用:
让方程更加接近“x=a”.
移项的依据:
等式性质1.
(1)移项要变号
(2)一般把含有x的项移到等号的左边,常数项移到等号的右边
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
做一做
方程 ,移项正确的是( )
A.
B.
C.
D.
B
移项,得
解析:
未变号
常数项应移到右边
-7未变号
探究新知
解下列方程
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
(1)
(2)
例3
(先移项再合并同类项)
(1)
解:
移项,得
合并同类项,得
系数化为1,得
探究新知
解下列方程
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例3
(1)
(2)
合并同类项,得
系数化为1,得
(2)
解:
移项,得
(先移项再合并同类项)
探究新知
解下列方程
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例3
(3)
移项,得
系数化为1,得
合并同类项,得
(3)
合并同类项,得
解:
小结:
(1)当方程两边各有可以合并的同类项时,可以根据情况先合并同类项再移项,减少出错.
(2)移项时注意变号.
(先合并同类项再移项)
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例4
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200t ;如用新工艺,则废水排量比环保限制的最大量少100t,新、旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?
分析: 旧工艺废水排量 = 环保限制的最大量 + 200,①
新工艺废水排量 = 环保限制的最大量 – 100,②
新工艺废水排量 :旧工艺废水排量 = 2 : 5. ③
如何设未知数呢?
直接设法:
间接设法:
设新、旧工艺的废水排量分别为 2x t 和 5x t.
方法1:设环保限制的最大量为 x t
间接设法需要引入x
方法2:设新工艺废水排量为 x t
方法3:设旧工艺废水排量为 x t
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
解法一:设新、旧工艺的废水排量分别为 2x t 和 5x t.
根据废水排量与环保限制最大量之间的关系,得
5x – 200 = 2x + 100.
移项,得 5x – 2x = 100 + 200.
合并同类项,得 3x = 300.
系数化为 1,得 x = 100.
所以 2x = 200,5x = 500.
答:新、旧工艺产生的废水排量分别为 200 t 和 500 t.
旧工艺废水排量 = 环保限制的最大量 + 200,①
新工艺废水排量 = 环保限制的最大量 – 100,②
新工艺废水排量 :旧工艺废水排量 = 2 : 5. ③
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
解法二:设环保限制的最大量为 a t,
根据条件①,得旧工艺废水排量为(a + 200)t,
根据条件②,得新工艺废水排量为(a – 100)t,
根据条件③,可列方程
(a – 100):(a + 200)= 2 : 5.
旧工艺废水排量 = 环保限制的最大量 + 200,①
新工艺废水排量 = 环保限制的最大量 – 100,②
新工艺废水排量 :旧工艺废水排量 = 2 : 5. ③
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
小结:
(1)未知数不同,等量关系不同,则所列方程就不同
(2)所的结果是相同的
解法三:设新工艺废水排量为 b t,
根据条件②,得环保限制的最大量为(b + 100)t,
根据条件①,得旧工艺废水排量为(b + 100 + 200)t,
根据条件③,可列方程
b :(b + 100 + 200)= 2 : 5.
旧工艺废水排量 = 环保限制的最大量 + 200,①
新工艺废水排量 = 环保限制的最大量 – 100,②
新工艺废水排量 :旧工艺废水排量 = 2 : 5. ③
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
解下列方程
(1)
(2)
(1)
解:
移项,得
合并同类项,得
系数化为1,得
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
(1)
(2)
解下列方程
(2)
解:
移项,得
合并同类项,得
系数化为1,得
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
在一张普通的月历中,相邻三行里同一列的三个日期数之和能否为30?如果能,这三个数分别是多少?
解:
设这三个数分别是 x,x+7,x+14.
根据相邻三行里同一列的三个日期数之和为30,列出方程
x+x+7+x+14=30.
解方程,得 x=3.
所以这三个数是3,10,17.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
解方程技巧:
移项:移项要变号
项数较多时,先合并同类项再移项
移项的依据:等式性质1
把等号一边的某项变号后移到另一边,叫做移项
移项后,方程的解不会改变
移项
通常把未知数移到等号的左边,把常数项移到右边
再见
