6.1 平均数 第2课时 课件(共20张PPT) 北师大版数学八年级上册
文档属性
| 名称 | 6.1 平均数 第2课时 课件(共20张PPT) 北师大版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 253.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 14:43:27 | ||
图片预览




文档简介
(共20张PPT)
第六章 数据的分析
6.1 平均数
第2课时
1.能熟练计算一组数据的加权平均数,理解加权对结果的影响
2.利用实际问题体会算术平均数和加权平均数的联系和区别
一、学习目标
二、新课导入
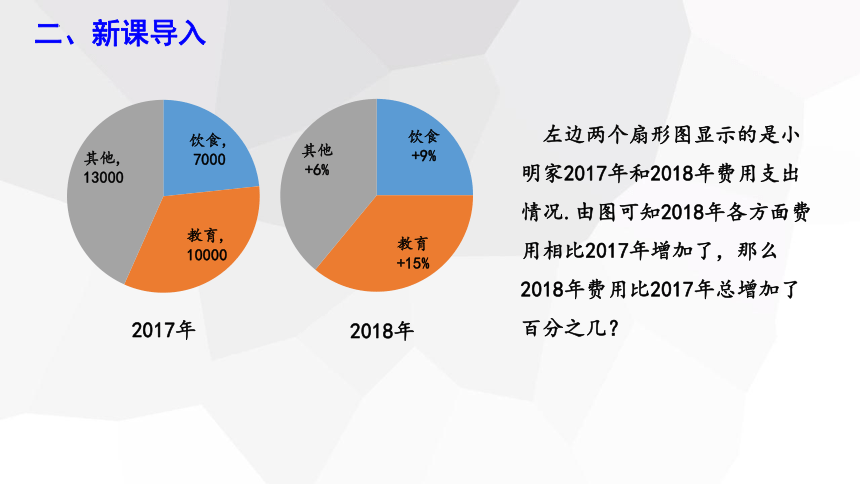
左边两个扇形图显示的是小明家2017年和2018年费用支出情况.由图可知2018年各方面费用相比2017年增加了,那么2018年费用比2017年总增加了百分之几?
2017年
2018年
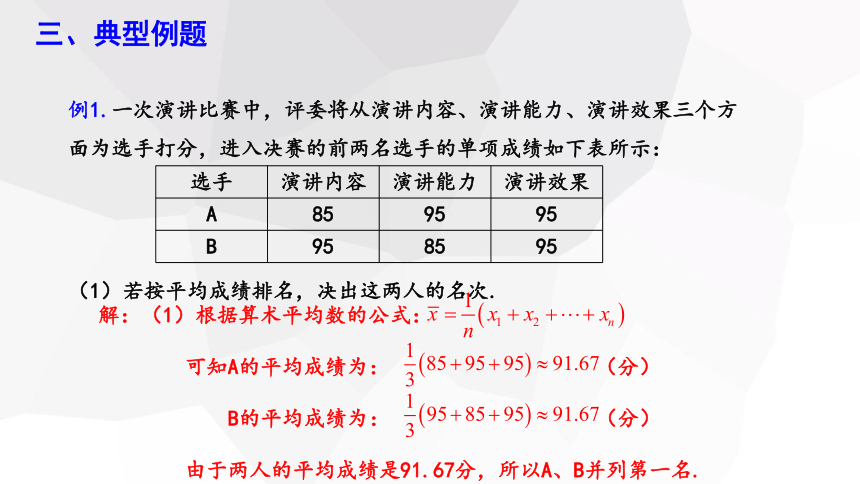
例1.一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,进入决赛的前两名选手的单项成绩如下表所示:
(1)若按平均成绩排名,决出这两人的名次.
解:(1)根据算术平均数的公式:
可知A的平均成绩为: (分)
B的平均成绩为: (分)
由于两人的平均成绩是91.67分,所以A、B并列第一名.
三、典型例题
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
(2)按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩,请决出两人的名次.
解:(2)根据题目可知:
A的平均成绩为: (分)
B的平均成绩为: (分)
由于91>90,所以B获得第一名,A获得第二名.
三、典型例题
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
【当堂检测】
解析:用加权平均数计算出每户居民每天丢弃到废旧塑料袋个数
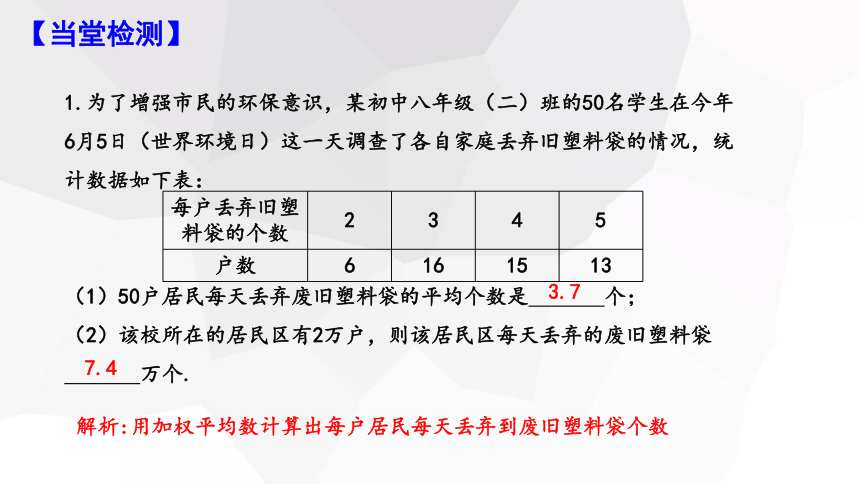
1.为了增强市民的环保意识,某初中八年级(二)班的50名学生在今年6月5日(世界环境日)这一天调查了各自家庭丢弃旧塑料袋的情况,统计数据如下表:
(1)50户居民每天丢弃废旧塑料袋的平均个数是 个;
(2)该校所在的居民区有2万户,则该居民区每天丢弃的废旧塑料袋
万个.
3.7
每户丢弃旧塑料袋的个数 2 3 4 5
户数 6 16 15 13
7.4
2.某校开展“节约每一滴水”的活动,从七年级的200名同学中任选出十名同学汇报了各自家庭一个月的节水情况,将有关数据整理如下表,请估计这200个家庭一个月节约用水的总量大约是( )
A.180吨 B.200吨 C.240吨 D. 360吨
解析:先通过 求出每个家庭节约用水量,
再通过计算得出200个家庭月节约用水总量.
【当堂检测】
节水量(吨) 0.5 1 1.5 2
同学数(人) 2 3 4 1
C
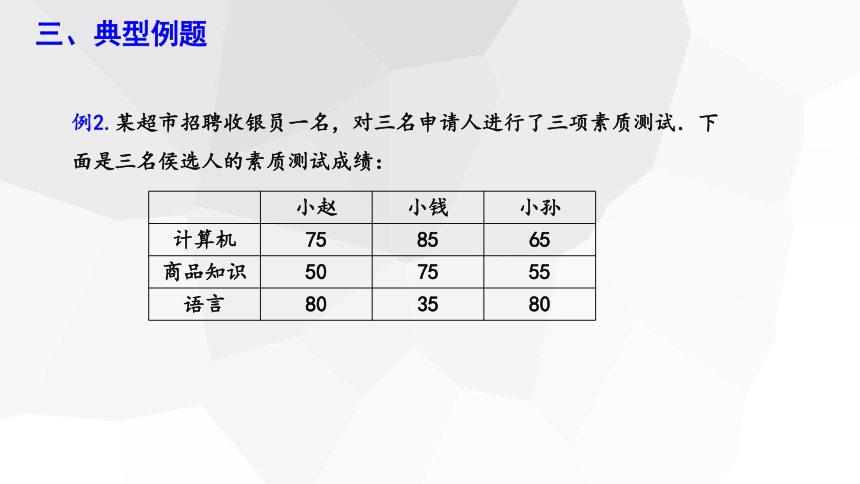
例2.某超市招聘收银员一名,对三名申请人进行了三项素质测试.下面是三名侯选人的素质测试成绩:
三、典型例题
小赵 小钱 小孙
计算机 75 85 65
商品知识 50 75 55
语言 80 35 80
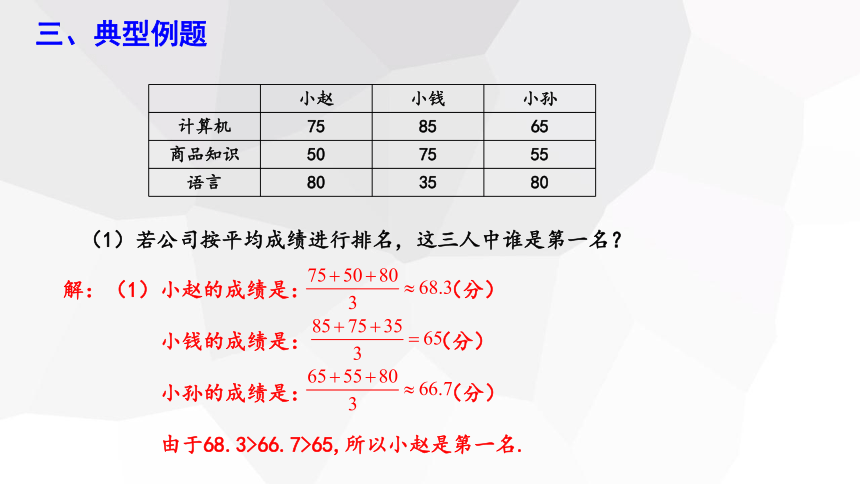
(1)若公司按平均成绩进行排名,这三人中谁是第一名?
三、典型例题
小赵 小钱 小孙
计算机 75 85 65
商品知识 50 75 55
语言 80 35 80
解:(1)小赵的成绩是: (分)
小钱的成绩是: (分)
小孙的成绩是: (分)
由于68.3>66.7>65,所以小赵是第一名.
(2)若公司根据实际需要,对计算机、商品知识、语言三项测试成绩按1:1:1的比例计算,这三人中谁是第一名?
三、典型例题
小赵 小钱 小孙
计算机 75 85 65
商品知识 50 75 55
语言 80 35 80
解:(2)小赵的成绩是: (分)
小钱的成绩是: (分)
小孙的成绩是: (分)
由于68.3>66.7>65,所以小赵是第一名.
(3)若公司根据实际需要,对计算机、商品知识、语言三项测试成绩按4:4:2的比例计算,这三人中谁是第一名?
三、典型例题
小赵 小钱 小孙
计算机 75 85 65
商品知识 50 75 55
语言 80 35 80
解:(3)小赵的成绩是: (分)
小钱的成绩是: (分)
小孙的成绩是: (分)
由于71>66>64,所以小钱是第一名.
(4)若公司根据实际需要,对计算机、商品知识、语言三项测试成绩按4:3:3的比例计算,这三人中谁是第一名?
三、典型例题
小赵 小钱 小孙
计算机 75 85 65
商品知识 50 75 55
语言 80 35 80
解:(4)小赵的成绩是: (分)
小钱的成绩是: (分)
小孙的成绩是: (分)
由于69>67>66.5,所以小赵是第一名.
总结:
三、典型例题
1.权的不同,会导致结果的不同,故权的差异对结果有影响.
2.算术平均数是加权平均数的一种特例,各项权相等且为1.
3.甲、乙两名大学生竞选班长,现对甲、乙两名应聘者从笔试、口试、得票三个方面表现进行评分,各项成绩如表所示:
(1)按两人平均成绩来判断,谁将竞选上?
【当堂检测】
应聘者 笔试 口试 得票
甲 85 83 90
乙 80 85 92
解:(1)甲的平均成绩是:(85+83+90)/3=86(分)
乙的平均成绩是:(80+85+92)/4=85.67(分)
由于86>85.67,故甲将竞选上班长.
(2)如果按笔试占总成绩20%、口试占30%、得票占50%来计算各人的成绩,试判断谁会竞选上?
【当堂检测】
解:(2)甲的成绩是: (分)
乙的成绩是: (分)
由于87.5>86.9,故乙将竞选上班长.
应聘者 笔试 口试 得票
甲 85 83 90
乙 80 85 92
(3)如果按笔试、口试、得票按2:1:2来计算各人的成绩,试判断谁会竞选上?
【当堂检测】
解:(3)甲的成绩是: (分)
乙的成绩是: (分)
由于86.6>85.5,故甲将竞选上班长.
应聘者 笔试 口试 得票
甲 85 83 90
乙 80 85 92
4.学校广播站要招聘1名记者,小亮和小丽报名参加了3项素质测试,成绩如下:
(1)将写作能力、普通话水平、计算机水平这三项的总分按3:5:2计算,则谁被录取?
解:(1)由题可知:小亮的总分是: (分)
小丽的总分是: (分)
由于74.4<74.7,所以小亮被录取.
【当堂检测】
写作能力 普通话水平 计算机水平
小亮 90分 75分 51分
小丽 60分 84分 72分
4.学校广播站要招聘1名记者,小亮和小丽报名参加了3项素质测试,成绩如下:
(2)若将写作能力、普通话水平、计算机水平这三项的总分改成按5:3:2计算,则谁被录取?
解:(2)由题可知:小亮的总分是: (分)
小丽的总分是: (分)
由于69.6<77.7,所以小亮被录取.
【当堂检测】
写作能力 普通话水平 计算机水平
小亮 90分 75分 51分
小丽 60分 84分 72分
4.学校广播站要招聘1名记者,小亮和小丽报名参加了3项素质测试,成绩如下:
(3)总分计算由(1)的比例改成(2)的,录取情况是否发生了变化,总分谁的浮动大?
解:(3)由(1)可知:小亮、小丽的总分分别是74.7、74.4,小亮被录取
由(2)可知:小亮、小丽的总分分别是77.7、69.6,小亮被录取
故小亮总分变化:77.7-74.7=3,增加了3分
小丽总分变化:69.6-74.4=-4.8,减少了4.8分
4.8>3,所以小丽总分浮动大,录取情况没有发生变化
【当堂检测】
写作能力 普通话水平 计算机水平
小亮 90分 75分 51分
小丽 60分 84分 72分
四、课堂总结
1.权的差异会对结果产生影响.
2.算术平均数是加权平均数的特例,算术平均数是加权平均数,但加权平均数不一定是算术平均数.
3.生活中的“平均”大多是“加权平均”.
第六章 数据的分析
6.1 平均数
第2课时
1.能熟练计算一组数据的加权平均数,理解加权对结果的影响
2.利用实际问题体会算术平均数和加权平均数的联系和区别
一、学习目标
二、新课导入
左边两个扇形图显示的是小明家2017年和2018年费用支出情况.由图可知2018年各方面费用相比2017年增加了,那么2018年费用比2017年总增加了百分之几?
2017年
2018年
例1.一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,进入决赛的前两名选手的单项成绩如下表所示:
(1)若按平均成绩排名,决出这两人的名次.
解:(1)根据算术平均数的公式:
可知A的平均成绩为: (分)
B的平均成绩为: (分)
由于两人的平均成绩是91.67分,所以A、B并列第一名.
三、典型例题
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
(2)按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩,请决出两人的名次.
解:(2)根据题目可知:
A的平均成绩为: (分)
B的平均成绩为: (分)
由于91>90,所以B获得第一名,A获得第二名.
三、典型例题
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
【当堂检测】
解析:用加权平均数计算出每户居民每天丢弃到废旧塑料袋个数
1.为了增强市民的环保意识,某初中八年级(二)班的50名学生在今年6月5日(世界环境日)这一天调查了各自家庭丢弃旧塑料袋的情况,统计数据如下表:
(1)50户居民每天丢弃废旧塑料袋的平均个数是 个;
(2)该校所在的居民区有2万户,则该居民区每天丢弃的废旧塑料袋
万个.
3.7
每户丢弃旧塑料袋的个数 2 3 4 5
户数 6 16 15 13
7.4
2.某校开展“节约每一滴水”的活动,从七年级的200名同学中任选出十名同学汇报了各自家庭一个月的节水情况,将有关数据整理如下表,请估计这200个家庭一个月节约用水的总量大约是( )
A.180吨 B.200吨 C.240吨 D. 360吨
解析:先通过 求出每个家庭节约用水量,
再通过计算得出200个家庭月节约用水总量.
【当堂检测】
节水量(吨) 0.5 1 1.5 2
同学数(人) 2 3 4 1
C
例2.某超市招聘收银员一名,对三名申请人进行了三项素质测试.下面是三名侯选人的素质测试成绩:
三、典型例题
小赵 小钱 小孙
计算机 75 85 65
商品知识 50 75 55
语言 80 35 80
(1)若公司按平均成绩进行排名,这三人中谁是第一名?
三、典型例题
小赵 小钱 小孙
计算机 75 85 65
商品知识 50 75 55
语言 80 35 80
解:(1)小赵的成绩是: (分)
小钱的成绩是: (分)
小孙的成绩是: (分)
由于68.3>66.7>65,所以小赵是第一名.
(2)若公司根据实际需要,对计算机、商品知识、语言三项测试成绩按1:1:1的比例计算,这三人中谁是第一名?
三、典型例题
小赵 小钱 小孙
计算机 75 85 65
商品知识 50 75 55
语言 80 35 80
解:(2)小赵的成绩是: (分)
小钱的成绩是: (分)
小孙的成绩是: (分)
由于68.3>66.7>65,所以小赵是第一名.
(3)若公司根据实际需要,对计算机、商品知识、语言三项测试成绩按4:4:2的比例计算,这三人中谁是第一名?
三、典型例题
小赵 小钱 小孙
计算机 75 85 65
商品知识 50 75 55
语言 80 35 80
解:(3)小赵的成绩是: (分)
小钱的成绩是: (分)
小孙的成绩是: (分)
由于71>66>64,所以小钱是第一名.
(4)若公司根据实际需要,对计算机、商品知识、语言三项测试成绩按4:3:3的比例计算,这三人中谁是第一名?
三、典型例题
小赵 小钱 小孙
计算机 75 85 65
商品知识 50 75 55
语言 80 35 80
解:(4)小赵的成绩是: (分)
小钱的成绩是: (分)
小孙的成绩是: (分)
由于69>67>66.5,所以小赵是第一名.
总结:
三、典型例题
1.权的不同,会导致结果的不同,故权的差异对结果有影响.
2.算术平均数是加权平均数的一种特例,各项权相等且为1.
3.甲、乙两名大学生竞选班长,现对甲、乙两名应聘者从笔试、口试、得票三个方面表现进行评分,各项成绩如表所示:
(1)按两人平均成绩来判断,谁将竞选上?
【当堂检测】
应聘者 笔试 口试 得票
甲 85 83 90
乙 80 85 92
解:(1)甲的平均成绩是:(85+83+90)/3=86(分)
乙的平均成绩是:(80+85+92)/4=85.67(分)
由于86>85.67,故甲将竞选上班长.
(2)如果按笔试占总成绩20%、口试占30%、得票占50%来计算各人的成绩,试判断谁会竞选上?
【当堂检测】
解:(2)甲的成绩是: (分)
乙的成绩是: (分)
由于87.5>86.9,故乙将竞选上班长.
应聘者 笔试 口试 得票
甲 85 83 90
乙 80 85 92
(3)如果按笔试、口试、得票按2:1:2来计算各人的成绩,试判断谁会竞选上?
【当堂检测】
解:(3)甲的成绩是: (分)
乙的成绩是: (分)
由于86.6>85.5,故甲将竞选上班长.
应聘者 笔试 口试 得票
甲 85 83 90
乙 80 85 92
4.学校广播站要招聘1名记者,小亮和小丽报名参加了3项素质测试,成绩如下:
(1)将写作能力、普通话水平、计算机水平这三项的总分按3:5:2计算,则谁被录取?
解:(1)由题可知:小亮的总分是: (分)
小丽的总分是: (分)
由于74.4<74.7,所以小亮被录取.
【当堂检测】
写作能力 普通话水平 计算机水平
小亮 90分 75分 51分
小丽 60分 84分 72分
4.学校广播站要招聘1名记者,小亮和小丽报名参加了3项素质测试,成绩如下:
(2)若将写作能力、普通话水平、计算机水平这三项的总分改成按5:3:2计算,则谁被录取?
解:(2)由题可知:小亮的总分是: (分)
小丽的总分是: (分)
由于69.6<77.7,所以小亮被录取.
【当堂检测】
写作能力 普通话水平 计算机水平
小亮 90分 75分 51分
小丽 60分 84分 72分
4.学校广播站要招聘1名记者,小亮和小丽报名参加了3项素质测试,成绩如下:
(3)总分计算由(1)的比例改成(2)的,录取情况是否发生了变化,总分谁的浮动大?
解:(3)由(1)可知:小亮、小丽的总分分别是74.7、74.4,小亮被录取
由(2)可知:小亮、小丽的总分分别是77.7、69.6,小亮被录取
故小亮总分变化:77.7-74.7=3,增加了3分
小丽总分变化:69.6-74.4=-4.8,减少了4.8分
4.8>3,所以小丽总分浮动大,录取情况没有发生变化
【当堂检测】
写作能力 普通话水平 计算机水平
小亮 90分 75分 51分
小丽 60分 84分 72分
四、课堂总结
1.权的差异会对结果产生影响.
2.算术平均数是加权平均数的特例,算术平均数是加权平均数,但加权平均数不一定是算术平均数.
3.生活中的“平均”大多是“加权平均”.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
